立体几何中球的内切和外接问题(完美版)

立体几何外接球及内切球问题一、球与柱体规则的柱体，如正方体、长方体、正棱柱等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱柱的棱产生联系，然后考查几何体的体积或者表面积等相关问题.1.1球与正方体如图1所示，正方体1111D C B A ABCD -,设正方体的棱长为a ，G H F E ,,,为棱的中点，O 为球的球心。

常见组合方式有三类：一是球为正方体的内切球，截面图为正方形EFHG 和其内切圆，则2a r OJ ==； 二是与正方体各棱相切的球，截面图为正方形EFHG 和其外接圆，则a R OG 22==； 三是球为正方体的外接球，截面图为长方形11A ACC 和其外接圆，则23'1a R O A ==. 例 1： 棱长为1的正方体的8个顶点都在球的表面上，分别是棱，的中点，则直线被球截得的线段长为（ ） A ．B ．C ． D1.2 球与长方体长方体各顶点可在一个球面上，故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为其体对角线为.当球为长方体的外接球时，截面图为长方体的对角面和其外接圆，和正方体的外接球的道理是一样的，故球的半径例 2 在长、宽、高分别为2，2，4的长方体内有一个半径为1的球，任意摆动此长方体，则球经过的空间1111ABCD A B C D -O E F ，1AA 1DD EF O 2112+,,,a b c l 2l R ==部分的体积为( ) A.10π3B.4πC.8π3D.7π31.3球与正棱柱：①结论：直三棱柱的外接球的球心是上下底面三角形外心的连线的中点. ②球与一般的正棱柱的组合体，常以外接形态居多.本类题目的解法：构造直角三角形法：设正三棱柱111C B A ABC -的高为h ，底面边长为a ； 如图2所示，D 和1D 分别为上下底面的中心。

根据几何体的特点，球心必落在高1DD 的中点O ，a AD R AO h OD 33,,2===，借助直角三角形AOD 的勾股定理，可求22332⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=a h R 。

八个超强模型——彻底解决立体几何的外接球和内切球问题摘要本文介绍了八个超强模型，这些模型可以用来彻底解决立体几何中的外接球和内切球问题。

每个模型都具有独特的特点和优势，能够有效地求解球的外接和内切问题，为立体几何的研究提供了有力的工具和方法。

引言在立体几何中，外接球和内切球问题是非常常见的问题。

求解这些问题通常需要借助一些数学模型和方法。

本文介绍了八个超强模型，这些模型在解决外接球和内切球问题方面表现出色。

模型一：球心法线模型该模型基于球的法线方程，通过求解法线方程的交点来得到球心坐标。

利用该模型可以快速准确地求解外接球和内切球的球心坐标。

模型二：点坐标向量模型该模型利用点的坐标向量来表示球心坐标，通过计算坐标向量的运算得到球心坐标。

该模型适用于各种类型的球体，求解效果良好。

模型三：坐标平移模型该模型基于坐标平移的概念，通过平移球心坐标来求解外接球和内切球的球心坐标。

该模型简单易懂，适用于多种立体几何结构。

模型四：线段接触模型该模型利用线段的接触点来求解外接球和内切球的球心坐标。

通过求解线段接触点的几何关系，可以得到球心坐标。

该模型适用于特定的立体几何结构。

模型五：平面交线模型该模型基于平面交线的概念，通过求解平面交线的方程来得到球心坐标。

该模型对于立体几何结构较复杂的情况下求解效果较好。

模型六：圆心半径模型该模型通过求解球的圆心和半径来得到球心坐标。

该模型适用于已知球的圆心和半径的情况下求解。

模型七：曲线拟合模型该模型通过对曲线进行拟合来得到球心坐标。

该模型适用于曲线较为复杂的情况下求解。

模型八：图像处理模型该模型利用图像处理的方法来得到球心坐标。

通过处理球体的图像，可以得到球心坐标。

该模型适用于图像处理技术较为成熟的情况下求解。

结论本文介绍了八个超强模型，这些模型可以用来彻底解决立体几何中的外接球和内切球问题。

每个模型都有其独特的特点和优势，能够有效地求解球的外接和内切问题。

这些模型为立体几何的研究提供了有力的工具和方法，有助于推动该领域的发展。

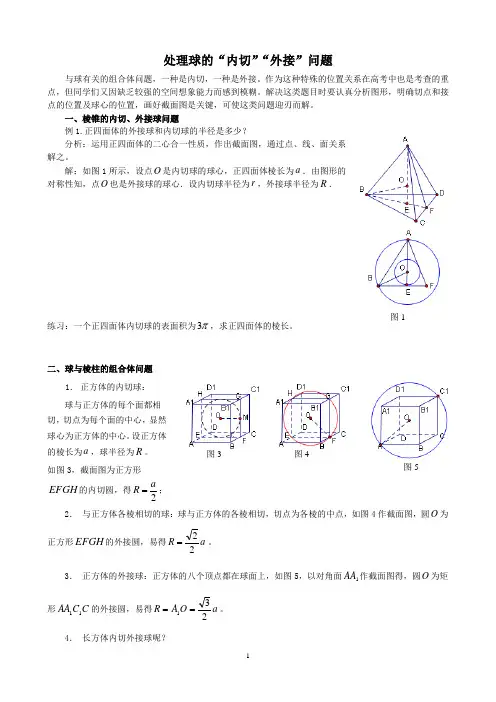
处理球的“内切”“外接”问题与球有关的组合体问题，一种是内切，一种是外接。

作为这种特殊的位置关系在高考中也是考查的重点，但同学们又因缺乏较强的空间想象能力而感到模糊。

解决这类题目时要认真分析图形，明确切点和接点的位置及球心的位置，画好截面图是关键，可使这类问题迎刃而解。

一、棱锥的内切、外接球问题例1.正四面体的外接球和内切球的半径是多少？分析：运用正四面体的二心合一性质，作出截面图，通过点、线、面关系解之。

解：如图1所示，设点O 是内切球的球心，正四面体棱长为a ．由图形的对称性知，点O 也是外接球的球心．设内切球半径为r ，外接球半径为R ．练习：一个正四面体内切球的表面积为π3，求正四面体的棱长。

二、球与棱柱的组合体问题1． 正方体的内切球：球与正方体的每个面都相切，切点为每个面的中心，显然球心为正方体的中心。

设正方体的棱长为a ，球半径为R 。

如图3，截面图为正方形EFGH 的内切圆，得2a R =； 2． 与正方体各棱相切的球：球与正方体的各棱相切，切点为各棱的中点，如图4作截面图，圆O 为正方形EFGH 的外接圆，易得a R 22=。

3． 正方体的外接球：正方体的八个顶点都在球面上，如图5，以对角面1AA 作截面图得，圆O 为矩形C C AA 11的外接圆，易得a O A R 231==。

4． 长方体内切外接球呢？图3 图4 图5 图1例3.在球面上有四个点P 、A 、B 、C .如果PA 、PB 、PC 两两互相垂直，且a PC PB PA ===,那么这个球的表面积是______.解：由已知可得PA 、PB 、PC 实际上就是球内接正方体中交于一点的三条棱，正方体的对角线长就是球的直径，连结过点C 的一条对角线CD ，则CD 过球心O ，对角线a CD 3=223234a a S ⋅=⎪⎪⎭⎫ ⎝⎛⋅=∴ππ球表面积 练习：1一棱长为a 2的框架型正方体，内放一能充气吹胀的气球，求当球与正方体棱适好接触但又不至于变形时的球的体积。

高考数学中的内切球和外接球问题一、有关外接球的问题如果一个多面体的各个顶点都在同一个球面上，那么称这个多面体是球的内接多面体，这个球称为多面体的外接球.有关多面体外接球的问题，是立体几何的一个重点，也是高考考查的一个热点.考查学生的空间想象能力以及化归能力.研究多面体的外接球问题，既要运用多面体的知识，又要运用球的知识，并且还要特别注意多面体的有关几何元素与球的半径之间的关系，而多面体外接球半径的求法在解题中往往会起到至关重要的作用.一、直接法（公式法）1、求正方体的外接球的有关问题例1若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为.例2一个正方体的各顶点均在同一球的球面上，若该正方体的表面积为24 ,则该球的体积为.2、求长方体的外接球的有关问题例3一个长方体的各顶点均在同一球面上，且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为.例4已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为（）.A. 16B. 20C. 24D. 323.求多面体的外接球的有关问题例5一个六棱柱的底面是正六边形， 其侧棱垂直于底面，已知该 六棱柱的顶点都在同一个球面上，且该六棱柱的体积为9,底面周长 为3,则这个球的体积为.解设正六棱柱的底面边长为x ,高为h ,则有 6x 3 9 会 3 2.6 — x h 8 4的半径的常用公式二、构造法（补形法）1、构造正方体例5若三棱锥的三条侧棱两两垂直，且侧棱长均为 V 3 ,则其外 接球的表面积是.例3若三棱锥的三个侧面两两垂直，且侧棱长均为V 3 ,则其外 接球的表面积是.故其外接球的表面积S 4 r 2 9 .小结：一般地，若一个三棱锥的三条侧棱两两垂直，且其长度分 别为a,b,c ,则就可以将这个三棱锥补成一个长方体， 于是长方体的体 对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则 有2R va 2 b 2 c 2.出现“墙角”结构利用补形知识，联系长方体。

立体几何中的“内切”与“外接”问题的探究(完美版)探究立体几何中“内切”与“外接”问题在立体几何中，我们经常遇到“内切”和“外接”的问题。

在研究这些问题之前，我们需要先明确球心的定义。

如果一个定点与一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体的外接球球心。

根据上述性质，我们可以得出以下多面体外接球的结论：1.正方体或长方体的外接球的球心是其体对角线的中点。

2.正棱柱的外接球的球心是上下底面中心的连线的中点。

3.直三棱柱的外接球的球心是上下底面三角形外心的连线的中点。

4.正棱锥的外接球的球心在其高上，具体位置可通过计算得到。

5.若棱锥的顶点可构成共斜边的直角三角形，则共斜边的中点就是其外接球的球心。

接下来我们来探究一下正方体和长方体的外接球的问题。

根据结论1，正方体或长方体的外接球的球心是其体对角线的中点。

我们可以利用构造法（补形法）来解决这类问题。

例如，对于一个长方体，如果从一个顶点出发的三条棱长分别为a、b、c，则体对角线长为√(a^2+b^2+c^2)，几何体的外接球直径2R为体对角线长l，因此R=√(a^2+b^2+c^2)/2.举个例子，如果一个三棱锥的三个侧面两两垂直，且侧棱长均为3，则可以将这个三棱锥补成一个棱长为3的正方体，于是正方体的外接球就是三棱锥的外接球。

设其外接球的半径为R，则有(2R)^2=3^2+3^2+3^2=27.因此，其外接球的表面积为S=4πR^2=36π。

另外，对于一个矩形ABCD，如果AB=4，BC=3，沿AC将矩形ABCD折成一个直二面角B-AC-D，则四面体ABCD的外接球的体积为(125π)/(1296)。

最后，如果出现正四面体外接球的问题，我们可以利用构造法（补形法），联系正方体。

一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为多少？解析：由于所有棱长都相等，所以可以构造一个正方体，再寻找棱长相等的四面体。

如图2所示，四面体ABDE满足条件，即AB=AD=AE=BD=DE=BE=2.由此可求得正方体的棱长为1，对角线为$\sqrt{3}$，从而外接球的直径也为$\sqrt{3}$，所以此球的表面积为$4\pi$，故选B。

图 6图3图4图5处理球的“内切”“外接”问题一、球与棱柱的组合体问题： 1、正方体的内切球：设正方体的棱长为a ，求（1）内切球半径；（2）外接球半径；（3）与棱相切的球半径。

（1）截面图为正方形EFGH 的内切圆，得2aR =；（2）与正方体各棱相切的球：球与正方体的各棱相切，切点为各棱的中点，如图4作截面图，圆O 为正方形EFGH 的外接圆，易得a R 22=。

（3） 正方体的外接球：正方体的八个顶点都在球面上，如图5，以对角面1AA 作截面图得，圆O 为矩形C C AA 11的外接圆，易得a O A R 231==。

2.在球面上有四个点P 、A 、B 、C .如果PA 、PB 、PC 两两互相垂直，且a PC PB PA ===,求这个球的表面积是______.解析：把该三棱锥嵌入棱长为a 的正方体中，则正方体的对角线长即为球的直径，故有 ()22222a a a R ++=，即2234a R =，所以球的表面积是2234a R ππ=。

3.已知底面边长为a 正三棱柱111C B A ABC -的六个顶点在球1O 上，又知球2O 与此正三棱柱 的5个面都相切，求球1O 与球2O 的体积之比与表面积之比。

分析：先画出过球心的截面图，再来探求半径之间的关系。

解：如图6，由题意得两球心1O 、2O 是重合的， 过正三棱柱的一条侧棱1AA 和它们的球心作截面， 设正三棱柱底面边长为a ，则a R 632=， 正三棱柱的高为a R h 3322==，由O D A Rt 11∆中， 得22222221125633333a a a R a R =⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+⎪⎪⎭⎫ ⎝⎛=，a R 1251=∴ 1:5::222121==∴R R S S ， 1:55:21=V V 二、棱锥的内切、外接球问题4 .棱长为a 的正四面体的外接球和内切球的半径是多少？分析：运用正四面体的二心合一性质，作出截面图，通过点、线、面关系解之。

立体几何中的外接球内切球棱切球问题1. 概述在立体几何中，外接球、内切球和棱切球是常见的几何问题。

它们在工程、建筑、数学等领域都有重要的应用。

本文将围绕外接球、内切球和棱切球展开讨论，探究它们的性质和相关问题。

2. 外接球的定义和性质外接球是指一个球与一个或多个其他物体外接，外接球的半径等于所外接物体相应部分的长度，在立体几何中有着重要的应用。

外接球的性质1）外接球的圆心在被外接物体向外伸出的法线上。

2）外接球的半径等于被外接物体的相应部分的长度。

3）对于凸体而言，外接球存在且唯一。

3. 内切球的定义和性质内切球是指一个球恰好与另一个物体相切，内切球在立体几何中也有着重要的应用。

内切球的性质1）内切球的圆心在被内切物体向内伸出的法线上。

2）对于凸体而言，内切球存在且唯一。

3）内切球在不同物体中的位置可能不同，但其存在性是唯一的。

4. 棱切球的定义和性质棱切球是指一个球与多个物体之间棱切的情况，在立体几何中也有着重要的应用。

棱切球的性质1）棱切球的圆心在被棱切物体所在的平面上。

2）对于凸体而言，棱切球存在且唯一。

3）棱切球在不同物体中的位置可能不同，但其存在性是唯一的。

5. 实际应用举例外接、内切和棱切球在实际应用中有着广泛的应用。

比如在建筑工程中，常常需要计算建筑物的外接球、内切球和棱切球，以确定其结构和稳定性。

在数学建模中，外接、内切和棱切球也常常出现，用于解决各种数学问题。

6. 结论外接球、内切球和棱切球是立体几何中重要的概念，它们的性质和应用涉及到广泛的领域。

对这些几何问题的深入研究和应用可以帮助我们更好地理解立体几何的性质，并且为实际问题的解决提供理论支持。

希望本文能够帮助读者更好地理解外接球、内切球和棱切球的相关问题，并且激发更多人对立体几何的兴趣和研究。

外接球、内切球和棱切球作为立体几何中的重要概念，其性质和应用不仅仅局限于几何学。

它们的相关问题还涉及到数学建模、工程设计、建筑结构等领域，对于实际问题的解决提供了理论支持和指导。

立体几何中的“内切”与“外接”问题的探究一、由球心的定义确定球心在空间，如果一个定点与一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体的外接球球心。

二、由上述性质可以得出以下多面体外接球的结论：结论1：正方体或长方体的外接球的球心是其体对角线的中点。

结论2：正棱柱的外接球的球心是上下底面中心的连线的中点。

结论3：直三棱柱的外接球的球心是上下底面三角形外心的连线的中点。

结论4：正棱锥的外接球的球心是在其高上，具体位置可通过计算得到。

结论5：若棱锥的顶点可构成共斜边的直角三角形，则共斜边的中点就是其外接球的球心。

一、定义法例1、 在矩形ABCD 中，4,3AB BC ==，沿AC 将矩形ABCD 折成一个直二面角B AC D --，则四面体ABCD 的外接球的体积为A.12512πB.1259πC.1256πD.1253π 解 设矩形对角线的交点为O ，则由矩形对角线互相平分，可知OA OB OC OD ===.∴点O 到四面体的四个顶点A B C D 、、、的距离相等，即点O 为四面体的外接球的球心，如图2所示.∴外接球的半径52R OA ==.故3412536V R ππ==球.选C.二、求正方体、长方体的外接球的有关问题结论1：正方体或长方体的外接球的球心是其体对角线的中点。

①出现“墙角”结构利用构造法(补形法)，联系长方体。

【原理】：长方体中从一个顶点出发的三条棱长分别为c b a ,,，则体对角线长为222c b a l ++=，几何体的外接球直径R 2为体对角线长l 即2222c b a R ++=例1、若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是 . 解 据题意可知，该三棱锥的三条侧棱两两垂直，∴把这个三棱锥可以补成一个棱长为3的正方体，于是正方体的外接球就是三棱锥的外接球.设其外接球的半径为R ，则有()()()()222223339R =++=.∴294R =. 故其外接球的表面积249S R ππ==.小结 一般地，若一个三棱锥的三条侧棱两两垂直，且其长度分别为a b c 、、，则就可以将这个三棱锥补成一个长方体，于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ，则有2222R a b c =++.②出现正四面体外接球时利用构造法(补形法)，联系正方体。

外接球问题江西省永丰中学陈保进若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球。

若一个定点到一个多面体的所有顶点的距离都相等，则这个定点就是该多面体外接球的球心。

以下为常见模型。

1、长方体模型结论：长方体的外接球的球心为其体对角线的中点，直径为体对角线。

公式：2222c b a R ++=（a ,b ,c 为长宽高）补充：以下情况可转化成长方体模型。

①若三棱锥的三条棱PA ,PB ,PC 两两互相垂直(墙角模型），则可在长方体中构造。

2222PC PB P A R ++=②正四面体P -ABC 可在正方体中构造，正方体棱长2=PA a ③若三棱锥的三组对棱两两相等，则可在长方体中构造。

设AC =BP =m ,AP =BC =n ,AB=PC =t ,则⎪⎩⎪⎨⎧=+=+=+222222222t c b n c a m b a ，三式相加,222222)(2t n m c b a ++=++2)2(2222222t n m c b a R ++=++=abc2、直三棱柱模型结论：直三棱柱外接球的球心是上、下底面外心连线的中点，222()2hR r =+r 为底面三角形外接圆的半径，可用正弦定理求，h 为直三棱柱的高。

补充：有一条侧棱垂直底面的三棱锥可补成直三棱柱，如图P -ABC 中，PA ⊥平面ABC ，则可补成直三棱柱PB 1C 1-ABC ,外接球半径公式同上。

提醒：底面具有外接圆的直棱柱才有外接球，比如正棱柱，且球心在上、下底面外心连线的中点，底面无外接圆的直棱柱，以及所有斜棱柱均无外接球。

3、共斜边模型四面体D-ABC 中，DC AD ⊥，BC AB ⊥，AC 为公共的斜边，O 为AC 的中点，则O 为四面体D-ABC 外接球的球心。

4、正棱锥模型外接球的球心在正棱锥的高所在直线上，如图正三棱锥A-BCD 中，作AO 1⊥平面BCD ，则易得BO 1=CO 1=DO 1，所以O 1为△BCD 的外心，设O 为其外接球球心，半径为R ，则BO =AO =R ,设AO 1=h ,BO 1=r ,则由BO 2=BO 12+OO 12,得R 2=r 2+(h-R )2。

立体几何外接圆球及内切圆球问题
立体几何是研究三维空间中的图形和体积的学科。

外接圆球和内切圆球问题是立体几何中常见的一个问题。

外接圆球问题
在立体几何中，外接圆球是指一个球能够刚好与一个多面体的所有顶点相切。

对于不规则多面体来说，外接圆球可能无法通过所有的顶点，但可以通过一部分顶点。

外接圆球的半径通常被称为外接球的半径，是从多面体的中心到多面体顶点的最远距离。

要计算外接球的半径，可以使用多面体的顶点坐标来求得多面体的边长和中心点的坐标，然后使用勾股定理来计算半径的长度。

内切圆球问题
内切圆球是指一个球刚好能够与多面体的所有面相切。

与外接
圆球问题类似，对于不规则多面体来说，内切圆球可能无法与所有
的面相切，但可以与一部分面相切。

内切圆球的半径通常被称为内切球的半径，是从多面体的中心
点到多面体的面的最短距离。

要计算内切球的半径，可以使用多面
体的面的法向量和距离公式来求得。

应用和意义
外接圆球和内切圆球问题在立体几何中具有重要的应用和意义。

它们可以用来解决很多实际问题，如计算多面体的体积、表面积，
以及优化多面体的设计。

外接圆球和内切圆球问题也被广泛应用于计算机图形学和计算
机辅助设计领域。

在三维建模和渲染中，可以使用外接圆球和内切
圆球来估计或近似多面体的几何特征，以便更高效地处理和渲染三
维模型。

结论
立体几何中的外接圆球和内切圆球问题是一个有趣且实用的领域。

通过计算外接球和内切球的半径，可以获得关于多面体的重要信息，并应用于多个领域，包括工程设计和计算机图形学。