当前位置：文档之家 › 内切球和外接球问题课件

内切球和外接球问题课件

  • 格式：ppt
  • 大小：785.50 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

关于球的内切和外接专题讲座课件人教新课标

关于球的内切和外接专题讲座课件人教新课标
球与多面体的内切、外接
D
C
A
B
D1
A1
高中数学教师欧阳文丰
O
C1
B1
一、复习
球体的体积与表面积
4
3
① V球 R
3
②
S球面 4 R
2
二、球与多面体的接、切
定义1：若一个多面体的各顶点都在一个球的球面上，
则称这个多面体是这个球的内接多面体，
这个球是这个多面体的外接球。
定义2：若一个多面体的各面都与一个球的球面相切，
类型二、求长方体外接球的有关问题
例2、一个长方体的各顶点均在同一球面上，
且一个顶点上的三条棱长分别为1,2,3 ，则此
球的表面积为
.
解析：关键是求出球的半径，因为长方体内接于
球，所以它的体对角线正好为球的直径。长方体
体对角线长为 14 ，故球的表面积为14 .
变式题：已知各顶点都在一个球面上的正四棱柱
球心到多面体各顶点的距离均相等
2、正多面体的内切球和外接球的球心重合
3、正棱锥的内切球和外接球球心都在高线上，但不
重合
4、基本方法：构造三角形利用类似比和勾股定理
5、体积分割是求内切球半径的通用做法
类型四、求正棱锥的外接球和内切球有关问题
例5、正三棱锥的高为 1，底面边长为
全面积和它的内切球的表面积。
2
a
2
a
3
r3
a
2
2a
•画出正确的截面：(1)中截面；(2)对角面
•找准数量关系
2a
类型一、球与正方体的“接切”问题
A
C
O
A1
C1
例1、若棱长为3的正方体的顶点都在同一球面

球的内切和外接问题课件

球的内切和外接问题课件

内切与外接问题的解题思路与方法
01
认真审题，明确题目中 的已知条件和所求目标 。
02
分析几何体的结构特征 ，确定内切或外接关系 。
03
合理利用内切或外接的 性质和定理，建立方程 或不等式求解。
04
对于复杂问题，可以采 用数形结合、分类讨论 等数学思想方法。
05
典型例题解析
简单几何体的内切与外接问题
判断一个球是否是多面体的内切球。
利用内切球的性质解决一些与多面体相关的问题，如求解多面体的体积、表面积等 。
外接球的定义与性质
定义
外接球是指一个球完全包含一个多面体，且与多面体的各个 顶点都相切。
性质
外接球的半径等于多面体外接圆半径，也等于从多面体中心 到任意一个顶点的距离。
外接球的计算方法
直接法
，也希望教师能够增加一些互动环节，提高课堂的趣味性。
对未来学习的建议与展望
加强基础知识的巩固
建议学生在课后加强对基础知识的学习和巩固，为后续的学习打下 坚实的基础。
增加实践环节
希望教师能够增加一些实践环节，如小组讨论、案例分析等，帮助 学生更好地应用所学知识解决实际问题。
拓展相关领域的学习
鼓励学生拓展相关领域的学习，如学习其他几何体的内切与外接问题 、了解相关数学史等，以拓宽视野并加深对课程内容的理解。
性质
内切球的半径等于多面体的内切圆半 径，也等于多面体各个面上的内切圆 半径的最小值。
内切球的计算方法
直接法
通过已知条件直接求出内切球的半径。
间接法
利用体积关系求出内切球的半径。对于棱锥、棱柱等多面体，可以先求出其体 积和表面积，再利用体积和表面积的关系求出内切球的半径。

空间几何体外接球问题精品课件(共27张ppt)全

空间几何体外接球问题精品课件(共27张ppt)全
（3）已知正四面体A-BCD，所有棱长都相等，点 A，B，C ，D都在球O 的表面上，如何求这个球的半径？
合作探究一：
（3）已知正四面体A-BCD，所有棱长都相等，点 A，B，C ，D都在球O 的表面上，如何求这个球的半径？
合作探究一：
（4）已知三棱锥 A-BCD，AB=CD=a，AD=BC=b，AC=BD=c，则三棱锥 A-BCD 外接球的半径?
合作探究二：
（5）已知正三棱锥 P-ABC，点 P，A，B，C 都在球 O 的表面上，顶点 P 到面 ABC 的距离为 h，底面△ABC 外接圆的半径为x，如何求这个球的半径？
O
O'
合作探究二：
（6）已知直三棱柱 ABC-A1B1C1，所有顶点都在球 O 的表面上，直三棱柱的高为 h，底面△ABC 外接圆的半径为x，如何求这个球的半径？
O
O'
O''
针对训练二： 1.正四棱锥的顶点都在同一球面上，若该棱锥的高为 4，底面边长为 2，则该球的表面积为（ ） A. B.16π C.9π D. 2. 正三棱柱 ABC-A1B1C1中，AA1=AB=2，则该三棱柱的外接球半径为__________.
空间几何体外接球问题
几何体与球的组合问题，一种是内切球，一种是外接球。纵观高考题，这种位置关系在高考中既是考查的热点，也是考查的难点，这是因为与球有关的几何体能很好地考察学生的空间想象能力以及化归能力。下面就常见几何体的外接球问题进行分析，找出规律，以便同学们更好地迎接高考。
已知正方体ABCD-A1B1C1D1的长、宽、高分别为a、b、c且它的8个顶点都在球面上，求这个球的半径？
长方体外接球的直径等于长方体的体对角线。
复习回顾：

与球有关的切接问题全解精品PPT课件

与球有关的切接问题全解精品PPT课件

·a2＝
3
a2，其内切球半径为正四面体高的
1 4
，即r＝
1 4
6 ·3
a＝
6 12
a，因此内切球表面积为S2＝4πr2＝
πa2 6
，则
S1 S2
＝ π63aa22＝6π3.
【变式训练】已知正三棱锥P-ABC的四个顶点均在半径为 3 的球面
上,且PA,PB,PC两两互相垂直,则球心到平面ABC的距离为
在截面三角形 SDC 内作一个与边 SD 和 DC 相切，
圆心在高 SE 上的圆．因为正四面体本身的对称性，内切球和外接
球的球心同为 O.此时，CO＝OS＝R，OE＝r，SE＝ 23a，CE＝
33a，则有 R＋r＝
23a，R2－r2＝|CE|2＝a32，解得
R
6 a,r 6 a
4
12
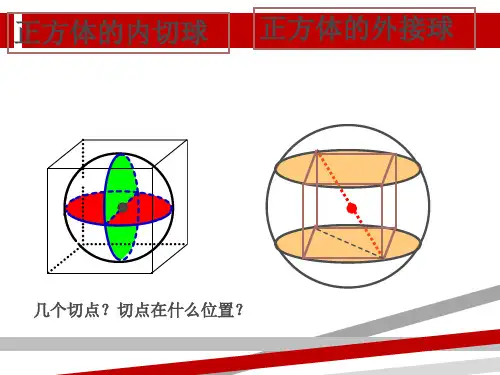
如果还原到正方体中去考虑呢？
球 O 的球面上，且 AB＝3，BC＝ 3，过点 D 作 DE 垂直 于平面 ABCD，交球 O 于 E，则棱锥 E-ABCD 的体积为 ________．
思考：可以还原到什么几何体中考虑？
解析
解析：如图所示，BE 过球心 O， ∴DE＝ 42－32－ 32＝2， ∴VE -ABCD＝13×3× 3×2＝2 3. 答案：2 3
练习 1.在正三棱锥 S-ABC 中，M 是 SC 的中点，且 AM
⊥SB，底面边长 AB＝2 2，则正三棱锥 S-ABC 的外接球
的表面积为
()
A．6π
B．12π
C．32π
D．36π
解析
解析：如图，由正三棱锥的性质易知 SB⊥AC，结合 AM⊥SB 知 SB⊥平 面 SAC，所以 SB⊥SA，SB⊥SC.又 正三棱锥的三个侧面是全等的三角 形，所以 SA⊥SC，所以正三棱锥 S-ABC 为正方体的一个角，所以正三棱锥 S-ABC 的外接 球即为正方体的外接球．由 AB＝2 2，得 SA＝SB＝SC ＝2，所以正方体的体对角线为 2 3，所以所求外接球的 半径 R＝ 3，所求表面积为 4πR2＝12π. 答案：B

球的内切与外接问题讲课

球的内切与外接问题讲课

综合应用举例
例1
解
已知一个三角形的三边长度，求其内切圆 半径和外接圆半径。
首先利用海伦公式求出三角形面积，再结 合半周长计算内切圆半径。对于外接圆半 径，可以通过正弦定理或余弦定理求解。
例2
解
给定一个正多边形，求其内切圆与外接圆 的半径比。
根据正多边形的性质，其所有内角相等， 且每条边与内切圆相切。由此可推导出内 切圆半径与外接圆半径的比例关系。
体对角线的长度来求解外接球的半径。
解答
03
长方体的体对角线长为$sqrt{3^2 + 4^2 + 5^2} = sqrt{50} =
5sqrt{2}$，因此其外接球的半径为$frac{5sqrt{2}}{2}$。
典型例题分析与解答
例题2
分析
已知一个正四面体的棱长为$a$，求其 外接球的半径。
正四面体的外接球半径可以通过构造 一个包含该正四面体的正方体来求解 。
长方体的内切球半径等于长方体相邻三条棱的倒数之和的倒数的一半，即 r=1/[(1/l)+(1/w)+(1/h)]。
解答
根据内切球的定义和性质，我们知道长方体的内切球半径等于长方体相邻三条棱的倒数之 和的倒数的一半。所以，r=1/[(1/l)+(1/w)+(1/h)]。
典型例题分析与解答
例题3
分析
解答
解答
构造一个棱长为$frac{sqrt{2}}{2}a$的 正方体，则该正方体的体对角线长等 于正四面体的外接球直径，即$2R = sqrt{(frac{sqrt{2}}{2}a)^2 + (frac{sqrt{2}}{2}a)^2 + (frac{sqrt{2}}{2}a)^2} = frac{sqrt{6}}{2}a$，因此正四面体的 外接球半径为$frac{sqrt{6}}{4}a$。

正四面体内切球和外接球(好用).ppt.ppt

正四面体内切球和外接球(好用).ppt.ppt
连结oaobocop那么abcabcabcabc1在一个倒置的正三棱锥容器内放入一个钢球钢球恰与棱锥的四个面都接触过棱锥的一条侧棱和高作截面正确的截面图形是3自球面上一点p作球的两两垂直的三条弦papbpc球的半径为r则pa
正方体的内切球
正方体的外接球
几个切点？切点在什么位置？
求棱长为a的正四面体的高.
A
[题组冲关] 3．假如某爱国实业家在20世纪初需要了解全国各地商业信
息，可采用的最快捷的方式是
(
)
A．乘坐飞机赴各地了解 B．通过无线电报输送讯息 C．通过互联网 D．乘坐火车赴各地了解
解析：本题考查中国近代物质生活的变迁。注意题干信 息“20世纪初”“最快捷的方式”，因此应选B，火车速度
远不及电报快。20世纪30年代民航飞机才在中国出现，
(2)1924年国民党“一大”召开，标志着第 一
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)20世纪初，孙中山提出“民族、民权、 民生”三民主义，成为以后辛亥革命 的
指导思想。 (2)三民主义没有明确提出反帝要求，也 没 有提出废除封建土地制度，是一个 不彻 底的资产阶级革命纲领。
报先后发明。
(3)近代以来，交通、通讯工具的进步，推 动了经济与社会的发展。
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)1911年，革命党人发动武昌起义，辛亥
革命
爆发，随后建立了中华民国，颁布了《中 华
民国临时约法》；辛亥革命是中国近代化
进 程的里程碑。
制了列强的经济侵略，但是并未能阻止其侵略。故B、C、D
三项表述都有错误。 答案：A

几何体内切球与外接球全解46页PPT

几何体内切球与外接球全解46页PPT

谢谢！
Байду номын сангаас
1、不要轻言放弃，否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意 去做，并愿意去冒险的人。“稳妥”之船，从未能从岸边走远。-戴尔．卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡，喝起来是苦涩的，回味起来却有 久久不会退去的余香。
几何体内切球与外接球全解 4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失 去今生对你的记忆，我不求天长地久的美景，我只要生生世世的轮 回里有你。
61、奢侈是舒适的，否则就不是奢侈 。——CocoCha nel 62、少而好学，如日出之阳；壮而好学 ，如日 中之光 ；志而 好学， 如炳烛 之光。 ——刘 向 63、三军可夺帅也，匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里，与其说好 的教师 是幸福 ，不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战，就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿

球的内切与外接问题讲课

球的内切与外接问题讲课

精选可编辑ppt
21
• 【思路点拨】 根据球截面性质找出 球半径与截面圆半径和球心到截面距 离的关系，求出球半径．
精选可编辑ppt
22
【解析】 如图所示，AB＝BC＝CD＝
DA＝SA＝SB＝SC＝SD＝ 2， O 为球心，球的半径为 R，
SO⊥平面 ABCD 于 M 点， ∵四边形 ABCD 为正方形，
2 S 球 85 26
精选可编辑ppt
15
例 、正三棱锥的高为 1，底面边长为 2 6 内有一个球与四个面都相切，求棱锥的全
面积和球的表面积。
A
在 Rt △ AO1E 中
sin 3 cos 6
1
O •θ
3
3
3
1cos
tan
3 2
2 sin
B
O1 E 在 Rt △ OO1E 中 OO 1 62
6
正方体的棱切球
精选可编辑ppt
7
精选可编辑ppt
8
精选可编辑ppt
9
正方体的棱 切球半径是 面对角线长 的一半
精选可编辑ppt
10
球与正方体的“接切”问题
典型：有三个球,一球切于正方体的各面,一球切 于正方体的各侧棱,一球过正方体的各顶点,求 这三个球的体积之比.
精选可编辑ppt
11
变题：
2 S 球 85 26
精选可编辑ppt
16
例 、正三棱锥的高为 1，底面边长为 2 6 内有一个球与四个面都相切，求棱锥的全
面积和球的表面积。
A
设球的半径为 r，则 VA- BCD =
VO-ABC + VO- ABD + VO-ACD + VO-BCD
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

• 结论1：正方体或长方体的外接球的球心其体对角 线的中点。
• 结论2：正棱柱的外接球的球心是上下底面中心的 连线的中点。
• 结论3：直三棱柱的外接球的球心是上下底面三角 形外心的连线的中点。
• 结论4：正棱锥的外接球的球心在其高上，具体位 置可通过计算找到。
• 结论5：若棱锥的顶点可构成共斜边的直角三角形， 则公共斜边的中点就是其外接球的球心。
正方体的内切球
例1
将棱长为2的正方体木块削成一个体积最 大的球，则这个球的表面积为 4
直棱柱的外接球
例2
已已知知直直三三棱棱柱柱AABBCCA1AB11BC11C的1的六六个个顶顶点点都在都在 球球OO的的球球面面上上,,若若AABBBCBC 1,1,ABACBC12012,0, AAAA11 22 33，，则则球球OO的的表表面面积积为为
几何体外接：一个几何体所有顶点都 在另一个几何体表面上。
正方体的内切球、棱切球、外接球
• 三、几何体的外接球与内切球问题：
• 1、外接球的问题： • 几何体外接球问题是立体几何中的难点和重要的
考点，此类问题实质是解决球的半径或确定球心0 的位置问题，其中球心的确定是关键。 • (1)由球的定义确定球心 • 在空间，如果一个定点与一个简单多面体的所有 顶点的距离都相等，那么这个定点就是该简单多 面体的外接球的球心。 • 由上述性质，可以得到确定简单多面体外接球的 球心的如下结论。
• 途径3：若已知棱锥含有线面垂直关系，则可将棱锥补成 长方体或正方体．
• 途径4：若三棱锥的三个侧面两两垂直，则可将三棱锥补 成长方体或正方体．
(3)由性质确定球心 利用球心与截面圆圆心的连线垂直于截面圆及球心与弦 中点的连线垂直于弦的性质，确定球心． 内切球的问题 对内切球有以下几点认识： 1、内切球球心到多面体各面的距离均相等，外接球球 心到多面体各顶点的距离均相等。 2、正多面体的内切球和外接球的球心重合。 3、正棱锥的内切球和外接球球心都在高线上，但不重 合。 4、基本方法：构造三角形利用相似比和勾股定理。 5、体积分割是求内切球半径的通用做法。
O o'
答案4π
例5、一个六棱柱的底面是正六边形，其侧棱垂直
于底面，已知该六棱柱的顶点都在同一个球面上，
且该六棱柱的体积为 ，底9 面周长为３，则这
个球的体积为
4。 8
3
补形成长方体
例6、如果三棱锥的三个侧面 两两垂直，它们的面积分别为 6、4、3，那么它的外接球的 表面积是29＿π.
a b
c
补形成长方体
答案 16π
棱锥的外接球
例 3、正四棱锥的顶点都在同一球
面上．若该棱锥的高为 4，底面边
长为 2，则该球的表面积为( )
A．814π
B．16π
C．9π
D．274π
答案A
例4、
四棱锥 P ABCD 所有顶点都在同一球面上， 若PA 平面ABCD，AB BC，AD CD，PA BC CD 1，AB AD 2，求该球的表面积.
• （2）构造正方体或长方体确定球心
• 长方体或正方体的外接球的球心是在其体对角线的中点 处．以下是常见的、基本的几何体补成正方体或长方体的 途径与方法．
• 途径1：正四面体、三条侧棱两两垂直的正三棱锥、四个 面都是是直角三角形的三棱锥都分别可构造正方体．
• 途径2：同一个顶点上的三条棱两两垂直的四面体、相对 的棱相等的三棱锥都分别可构造长方体和正方体．
例7、在三棱锥中A-BCD
中,AB=CD=2,AD=BC=3,AC=BD=4，则三棱锥A-BCD外 接球的表面积 .
，
A
c
bC a
B D
思考题：例8、半径为R的球的外切圆柱(球与圆柱 的侧面、两底面都相切)的表面积为_6__R_2，体积 2__R_3_．
内接球、外接球问题
1．球的概念
•球的旋转定义
半圆以它的直径为旋转轴，旋转所 成的曲面叫做球面.球面所围成的几 何体叫做球体.
Hale Waihona Puke •球的集合定义与定点的距离等于定长的点的集合,叫 做球面
与定点的距离等于或小于定长的 点的集合，叫做球体，简称“球”.
二 球的性质
性质1：用一个平面去截球，截面是圆面；
用一个平面去截球面， 截线是圆。
大圆--截面过球心，半径等于球半径； 小圆--截面不过球心
性质2: 球心和截面圆心的连线垂
直于截面．
性质3: 球心到截面的距离d与球
的半径R及截面的半径r 有下面的关
系:
A
r R2 d2
类型：内切球、棱切球、外接球
几何体相切：一个几何体各个面分别 与另一个几何体各个面相切。
几何体棱切：一个几何体各个面分 别与另一个几何体各条棱相切。