空间几何体的外接球和内切球问题说课材料

内切与外接问题的解题思路与方法
01
认真审题，明确题目中 的已知条件和所求目标 。
02
分析几何体的结构特征 ，确定内切或外接关系 。
03
合理利用内切或外接的 性质和定理，建立方程 或不等式求解。
04
对于复杂问题，可以采 用数形结合、分类讨论 等数学思想方法。
05
典型例题解析
简单几何体的内切与外接问题
判断一个球是否是多面体的内切球。
利用内切球的性质解决一些与多面体相关的问题，如求解多面体的体积、表面积等 。
外接球的定义与性质
定义
外接球是指一个球完全包含一个多面体，且与多面体的各个 顶点都相切。
性质
外接球的半径等于多面体外接圆半径，也等于从多面体中心 到任意一个顶点的距离。
外接球的计算方法
直接法
，也希望教师能够增加一些互动环节，提高课堂的趣味性。
对未来学习的建议与展望
加强基础知识的巩固
建议学生在课后加强对基础知识的学习和巩固，为后续的学习打下 坚实的基础。
增加实践环节
希望教师能够增加一些实践环节，如小组讨论、案例分析等，帮助 学生更好地应用所学知识解决实际问题。
拓展相关领域的学习
鼓励学生拓展相关领域的学习，如学习其他几何体的内切与外接问题 、了解相关数学史等，以拓宽视野并加深对课程内容的理解。
性质
内切球的半径等于多面体的内切圆半 径，也等于多面体各个面上的内切圆 半径的最小值。
内切球的计算方法
直接法
通过已知条件直接求出内切球的半径。
间接法
利用体积关系求出内切球的半径。对于棱锥、棱柱等多面体，可以先求出其体 积和表面积，再利用体积和表面积的关系求出内切球的半径。

空间几何体的外接球与内切球问题高考分析： 球与几何体的切接问题是近几年高考的高频考点，常以选择题和填空题的形式出现，以中档题和偏难题为主. 一、几种常见几何体的外接与内切球 1.长方体的外接球 (1)球心：体对角线的交点；(2)半径：R ＝a 2＋b 2＋c 22(a ，b ，c 为长方体的长、宽、高)．2.正方体的外接球、内切球及与各条棱相切的球 (1)外接球：球心是正方体的中心；半径R ＝32a(a 为正方体的棱长)； (2)内切球：球心是正方体的中心；半径r ＝2a(a 为正方体的棱长)；(3)与各条棱都相切的球：球心是正方体的中心；半径=2r a (a 为正方体的棱长)． 3.正四面体的外接球与内切球(1)外接球：球心是正四面体的中心；半径R (a 为正四面体的棱长)；(2)内切球：球心是正四面体的中心；半径r (a 为正四面体的棱长)．求外接球问题常用方法：1.补体法。

将几何体补形成长方体正方体等常见模型去求解2.外接球的球心都在过底面外接圆圆心的垂线上（注意球体可以滚动所以可以选择较为方便计算的那一面作为底面）3.利用外接球球心到几何体各顶点距离都等于半径4.球心与截面圆圆心的连线垂直于截面圆求外接球的关键是确定球心位置，进而计算出外接球半径。

题型一：柱体的外接球1.已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为_________．2.已知三棱柱111ABC A B C －的底面是边长为6的正三角形，侧棱垂直于底面，且该三棱柱的外接球的表面积为12 ，则该三棱柱的体积为_________．3.已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是( )A ．16πB ．20πC ．24πD ．32π4.已知圆柱的底面半径为12，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A.πB.3π4 C.π2 D.π4题型二：锥体的外接球5.求棱长为1的正四面体外接球的体积为_________．6.已知正四棱锥P －ABCD 内接于一个半径为R 的球，则正四棱锥P －ABCD 体积的最大值是( )A.16R 381B.32R 381C.64R 381 D ．R 3 7.如图，在四棱锥P －ABCD 中，底面ABCD 为菱形，PB ⊥底面ABCD ，O 为对角线AC 与BD 的交点，若PB ＝1，∠APB ＝∠BAD ＝π3，则三棱锥P －AOB 的外接球的体积是_________．8.已知△ABC 是面积为的等边三角形，且其顶点都在球O 的球面上.若球O 的表面积为16π，则O 到平面ABC 的距离为（ ） A.B.C. 1D.9.已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC 的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为（ ）A. 64πB. 48πC. 36πD. 32π10.《九章算术》中对一些特殊的几何体有特定的称谓，例如：将底面为直角三角形的直三棱柱称为堑堵．将一堑堵沿其一顶点与相对的棱切开，得到一个阳马(底面是长方形，且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均是直角三角形的四面体)．在如图所示的堑堵ABC －A 1B 1C 1中，AA 1＝AC ＝5，AB ＝3，BC ＝4，则阳马C 1－ABB 1A 1的外接球的表面积是( )A ．25πB ．50πC ．100πD ．200π11.已知三棱锥P −ABC 的四个顶点在球O 的球面上，PA =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°，则球O 的体积为 A ．68πB ．64πC ．62πD ．6π12.已知正三棱锥的所有顶点都在球O 的球面上，其底面边长为3，E,F ,G 分别为为侧棱AB,AC,AD 的中点.若O 在三棱锥A -BCD 内，且三棱锥A -BCD 的体积是三棱锥O -BCD 体积的3倍，则平面EFG 截球O 所得截面的面积为微专题 球与几何体的切接问题——内切球1.半径为R 的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为_________，体积为_________．2.若正四面体的棱长为a ，则其内切球的半径为_________．3.已知正三棱锥的高为6，内切球(与四个面都相切)的表面积为16π，则其底面边长为( ) A ．18 B ．12 C ．6 3 D ．434.将半径为3，圆心角为2π3的扇形围成一个圆锥(接缝处忽略不计)，则该圆锥的内切球的体积为( )A.2π3 B.3π3 C.4π3D ．2π 5.如图，已知球O 是棱长为1的正方体ABCD －A 1B 1C 1D 1的内切球，则平面ACD 1截球O 的截面面积为( )A.66π B.π3 C.π6 D.33π题型三 最值问题6.已知底面是正六边形的六棱锥P －ABCDEF 的七个顶点均在球O 的表面上，底面正六边形的边长为1，若该六棱锥体积的最大值为3，则球O 的表面积为_________．7.四棱锥S －ABCD 的所有顶点都在同一球面上，底面ABCD 是正方形且和球心O 在同一平面内，当此四棱锥的体积取得最大值时，其表面积等于8＋83，则球O 的体积等于( )A.32π3B.322π3 C ．16π D.162π38.已知SAB 是边上为2的等边三角形，045ACB ∠=，则三棱锥体积最大时，CA = ;其外接球的表面积为。

)
A.4 3π
B.8π
C.12π
D.20π
解析：在底面△ABC 中，由正弦定理得底面△ABC 外接圆的
半径为
r＝2sin B∠CBAC＝2sin2
3π＝ 4
2.
直三棱柱 ABC-A1B1C1 的外接球的半径 R＝ ( 2)2＋12＝ 3，
r2＋A2A12＝
则直三棱柱 ABC-A1B1C1 的外接球的体积为43πR3＝4 3π.
当
λ＝12时，cos〈E→B，E→G〉＝2
3
2 .
∴cos〈E→B，E→G〉的最大值为2
3
2 .
∵A→C＝(－1，1，0)，A→F＝(0，1，1)， ∴E→B·A→C＝E→B·A→F＝0. ∴EB⊥AC，EB⊥AF. ∵AC∩AF＝A，∴EB⊥平面 AFC. ∵E→B·E→G>0，∴cos〈E→B，E→G〉即为 EG 与平面 AFC 所成角
如图 6-7 所示，把四面体 S-ABC 补全为长方体 ABCD-SPMN， 其中 SA，AB，BC 为长方体中首尾相连且两两相互垂直的三条棱， 点 H 为 PM 中点.
图 6-7
∵GH∥AP，∴G，H 两点到平面 AEF 的距离相等.
设点 H 到平面 AEF 的距离为 d.
∵△APF 是边长为 2 2的等边三角形，
[例 1]已知一个圆锥底面半径为 1，母线长为 3，则该圆锥内
切球的表面积为( )
A.π
B.32π
C.2π
D.3π
解析：依题意，作出圆锥与球的轴截面，如图
6-1 所示.设球的半径为 r，易知轴截面三角形边 AB
上的高为 2 2，因为△SOD∽△SBE，所以SSOB＝OBED，
即2 32－r＝1r，解得 r＝ 22.所以圆锥内切球的表面

A. 4π
B. 12π
C. 16π
D.
32 3
π
·8· 惊叹数学的波澜壮阔之势 赏析数学的对称和谐之美！
领悟数学的高瞻远瞩之能 铸就数学的茅塞顿开之境！
学习数学 领悟数学 满分数学
7. (2021• 咸阳模拟 ) 在直三棱柱 ABC
- A1B1C1 中，AB = BC = 2，∠ABC =
π 2
，若该直三棱柱的外接球表面积
棱锥体积的最大值为
3
3 4
，则其外接球的半径为
(
)
A. 1
B. 2
C. 3
D.
2 3
3 ，AC = 3，若该三
考点四 含二面角的外接球终极公式
双距离单交线公式：R2 =
m2 + n2 − 2mncosα sin2α
+
l2 4
如下图，若空间四边形 ABCD 中，二面角 C − AB − D 的平面角大小为 α，ABD 的外接球球心为 O1，ABC 的外
为 16π，则此直三棱柱的高为（ ）
A. 4
B. 3
C. 4 2
D. 2 2
图1
图2
8. (2021• 呼和浩特一模 ) 四面体 ABCD 的四个顶点都在球 O 上，且 AB = AC = BC = BD = CD = 4，AD =
2 6 ，则球 O 的表面积为（ ）
A.
70π 3
B.
80π 3
C. 30π
接球球心为 O2，E 为公共弦 AB 中点，则 ∠O1EO2 = α，O1E = m，O2E = n，AE =
l 2
，OA = R，由于 O、O1、E、O2
四点共球，且 OE = 2R =

空间几何体的外接球和内切球问题空间几何体的外接球和内切球问题类型1 外接球的问题1.必备知识：(1)简单多面体外接球的球心的结论.结论1：正方体或长方体的外接球的球心是其体对角线的中点.结论2：正棱柱的外接球的球心是上下底面中心的连线的中点.结论3：直三棱柱的外接球的球心是上下底面三角形外心的连线的中点.(2)构造正方体或长方体确定球心.(3)利用球心O 与截面圆圆心O 1的连线垂直于截面圆及球心O 与弦中点的连线垂直于弦的性质，确定球心.2.方法技巧：（1）几何体补成正方体或长方体.（2）轴截面法（3）空间向量法1AB DC AD BC BD AC ======例1-1、正四面体的棱长都为，求此四面体外接球和内切球的半径例1-2、四面体中，， 求此四面体外接球的表面积 例1-3．若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（ ）A.3B.6C.36D.9训练1（创新110页） 某几何体的三视图如图所示，则该几何体的外接球的表面积为( )A.25πB.26πC.32πD.36π训练2（创新110页）已知边长为2的等边三角形ABC ，D 为BC 的中点，沿AD 进行折叠，使折叠后的∠BDC ＝π2，则过A ，B ，C ，D 四点的球的表面积为( ) A.3π B.4π C.5π D.6π例2-1（创新110页）体积为3的三棱锥P －ABC 的顶点都在球O 的球面上，P A ⊥平面ABC ，P A ＝2，∠ABC ＝120°，则球O 的体积的最小值为( ) A.773π B.2873π C.19193π D.76193π 例2-1（创新109页）三棱锥P －ABC 中，平面P AC ⊥平面ABC ，AB ⊥AC ，P A ＝PC ＝AC ＝2，AB ＝4，则三棱锥P －ABC 的外接球的表面积为( )A.23πB.234πC.64πD.643π 类型2 内切球问题1.必备知识：(1)内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等.(2)正多面体的内切球和外接球的球心重合. (3)正棱锥的内切球和外接球球心都在高线上，但不一定重合.2.方法技巧：体积分割是求内切球半径的通用做法.【例3】 体积为4π3的球与正三棱柱的所有面均相切，则该棱柱的体积为________. 空间几何体的外接球和内切球问题近几年高考题1、（2019全国1卷第12题）已知三棱锥P ABC -的四个顶点在球O 的球面上，PA PB PC ==，△ABC 是边长为2的正三角形，E ，F 分别是PA ，PB 的中点，90CEF ∠=︒，则球O 的体积为（ ）A ．B ．C ． D2、（2018全国3卷第10题）．设A B C D ，，，是同一个半径为4的球的球面上四点，ABC △为等边三角形且其面积为D ABC -体积的最大值为（ ）A ．B ．C ．D ．3．（2017全国1卷第16题）如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O .D ，E ，F 为圆O 上的点，△DBC ，△ECA ，△FAB 分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ，CA ，AB 为折痕折起△DBC ，△ECA ，△FAB ，使得D ，E ，F 重合，得到三棱锥．当△ABC 的边长变化时，所得三棱锥体积(单位：cm 3)的最大值为______．4、（2017新课标全国Ⅲ理科）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（ ）A.πB.3π4 C.π2 D.π4 5、（2016年全国1卷第6题）．如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3，则它的表面积是 ( )（A ）17π （B ）18π （C ）20π （D ）28π6、（2016年全国3卷第10题）在封闭的直三棱柱ABC −A 1B 1C 1内有一个体积为V 的球，若AB ⊥BC ，AB =6，BC =8，AA 1=3，则V 的最大值是( ) (A)4π (B)9π2 (C)6π (D)32π37、（2015年全国1卷第11题）．圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20π，则r=（ ）（A ） 1 （B）2 （C ）4 （D ）88、（2015年全国2卷第9题）．已知是球的球面上两点,,为该球面上的动点.若三棱锥体积的最大值为36,则球的表面积为（ ） A ．36πB ．64πC ．144πD ．256π 7.(2014·大纲全国，8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4，底面边长为2，则该球的表面积为( )A.81π4B.16πC.9πD.27π49、（2013年课标1卷第6题）、如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为( )A 、500π3cm 3B 、866π3cm 3C 、1372π3cm 3D 、2048π3cm 310、（2012课标卷第11题）已知三棱锥S ABC -的所有顶点都在球O 的求面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =；则此棱锥的体积为（ ）()A 26 ()B 36 ()C 23 ()D 2211、（2011课标卷第15题）已知矩形的顶点都在半径为4的球的球面上，且,则棱锥的体积为 。

八个有趣模型——搞定空间几何体的外接球与内切球一、有关定义1．球的定义：空间中到定点的距离等于定长的点的集合（轨迹）叫球面，简称球.2．外接球的定义：若一个多面体的各个顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球.3．内切球的定义：若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球.二、外接球的有关知识与方法1．性质：性质1：过球心的平面截球面所得圆是大圆，大圆的半径与球的半径相等；性质2：经过小圆的直径与小圆面垂直的平面必过球心，该平面截球所得圆是大圆；性质3：过球心与小圆圆心的直线垂直于小圆所在的平面（类比：圆的垂径定理）；性质4：球心在大圆面和小圆面上的射影是相应圆的圆心；性质5：在同一球中，过两相交圆的圆心垂直于相应的圆面的直线相交，交点是球心（类比：在同圆中，两相交弦的中垂线交点是圆心）.初图1初图22．结论：结论1：长方体的外接球的球心在体对角线的交点处，即长方体的体对角线的中点是球心；结论2：若由长方体切得的多面体的所有顶点是原长方体的顶点，则所得多面体与原长方体的外接球相同；结论3：长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心，换言之，就是：底面的一条对角线与一条高（棱）构成的直角三角形的外接圆是大圆；结论4：圆柱体的外接球球心在上下两底面圆的圆心连一段中点处；结论5：圆柱体轴截面矩形的外接圆是大圆，该矩形的对角线（外接圆直径）是球的直径；结论6：直棱柱的外接球与该棱柱外接圆柱体有相同的外接球；结论7：圆锥体的外接球球心在圆锥的高所在的直线上；结论8：圆锥体轴截面等腰三角形的外接圆是大圆，该三角形的外接圆直径是球的直径；结论9：侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3．终极利器：勾股定理、正定理及余弦定理（解三角形求线段长度）；三、内切球的有关知识与方法1．若球与平面相切，则切点与球心连线与切面垂直.（与直线切圆的结论有一致性）.2．内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等.（类比：与多边形的内切圆）.3．正多面体的内切球和外接球的球心重合.4．正棱锥的内切球和外接球球心都在高线上，但不一定重合.5．基本方法：（1）构造三角形利用相似比和勾股定理；（2）体积分割是求内切球半径的通用做法（等体积法）.四、与台体相关的，此略.五、八大模型第一讲 柱体背景的模型类型一、墙角模型（三条棱两两垂直，不找球心的位置即可求出球半径）图1-1图1-2图1-3图1-4方法：找三条两两垂直的线段，直接用公式2222)2(c b a R ++=，即2222c b a R ++=，求出R 例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ C ） A ．π16 B ．π20 C ．π24 D ．π32解： 162==h a V ，2=a ，24164442222=++=++=h a a R ，π24=S ，选C ；（2）若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是 π9 解：933342=++=R ，ππ942==R S ；（3）在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 .π36 解：引理：正三棱锥的对棱互相垂直.证明如下：如图（3）-1， 取BC AB ,的中点E D ,，连接CD AE ,，CD AE ,交于H ，连接SH ， 则H 是底面正三角形ABC 的中心，∴⊥SH 平面ABC ，∴AB SH ⊥，BC AC =，BD AD =，∴AB CD ⊥，∴⊥AB 平面SCD ，∴SC AB ⊥，同理：SA BC ⊥，SB AC ⊥，即正三棱锥的对棱互垂直， 本题图如图（3）-2， MN AM ⊥，MN SB //，∴SB AM ⊥， SB AC ⊥，∴⊥SB 平面SAC ， ∴SA SB ⊥，SC SB ⊥， SA SB ⊥，SA BC ⊥， ∴⊥SA 平面SBC ，∴SC SA ⊥，故三棱锥ABC S -的三棱条侧棱两两互相垂直，∴36)32()32()32()2(2222=++=R ，即3642=R ，∴正三棱锥ABC S -外接球的表面积是π36.(3)题-1(引理）AC(3)题-2（解答图）AC（4）在四面体S ABC -中，ABC SA 平面⊥，,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为（ D ）π11.A π7.B π310.C π340.D 解：在ABC ∆中，7120cos 2222=⋅⋅-+=BC AB AB AC BC ，7=BC ，ABC ∆的外接球直径为372237sin 2==∠=BACBCr ，∴3404)372()2()2(2222=+=+=SA r R ，340π=S ，选D （5）如果三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是 解：由已知得三条侧棱两两垂直，设三条侧棱长分别为c b a ,,（+∈R c b a ,,），则⎪⎩⎪⎨⎧===6812ac bc ab ，∴24=abc ，∴3=a ，4=b ，2=c ，29)2(2222=++=c b a R ，ππ2942==R S ， （6）已知某几何体的三视图如图所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体外接球的体积为 解：3)2(2222=++=c b a R ，432=R ，23=R πππ2383334343=⋅==R V 球，类型二、对棱相等模型（补形为长方体） 题设：三棱锥（即四面体）中，已知三组对棱分别相等，求外接球半径（CD AB =，BC AD =，BD AC =） 第一步：画出一个长方体，标出三组互为异面直线的对棱； 第二步：设出长方体的长宽高分别为c b a ,,，x BC AD ==，y CD AB ==，z BD AC ==，列方程组，⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=， 补充：图2-1中，abc abc abc V BCD A 31461=⨯-=-. (6)题图（6）题直观图P图2-1第三步：根据墙角模型，22222222z y x c b a R ++=++=，82222z y x R ++=，8222z y x R ++=，求出R .思考：如何求棱长为a 的正四面体体积，如何求其外接球体积？例2（1）如下图所示三棱锥A BCD -，其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .解：对棱相等，补形为长方体，如图2-1，设长宽高分别为c b a ,,，110493625)(2222=++=++c b a ，55222=++c b a ，5542=R ，π55=S(1)题图B（2）在三棱锥BCD A -中，2==CD AB ，3==BC AD ，4==BD AC ，则三棱锥BCD A -外接球的表面积为 .π229 解：如图2-1，设补形为长方体，三个长度为三对面的对角线长，设长宽高分别为c b a ,,，则922=+b a ，422=+c b ，1622=+a c ∴291649)(2222=++=++c b a ，291649)(2222=++=++c b a ， 229222=++c b a ，22942=R ，π229=S （3）正四面体的各条棱长都为2，则该正面体外接球的体积为 （3）解答题解：正四面体对棱相等的模式，放入正方体中，32=R ，23=R ，ππ2383334=⋅=V （4）棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如下图，则图中三角形(正四面体的截面)的面积是 .(4)题解答图(4)题解：如解答图，将正四面体放入正方体中，截面为1PCO ∆，面积是2.类型三、汉堡模型（直棱柱的外接球、圆柱的外接球）图3-1图3-2 图3-3题设：如图3-1，图3-2，图3-3,直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）第一步：确定球心O 的位置，1O 是ABC ∆的外心，则⊥1OO 平面ABC ； 第二步：算出小圆1O 的半径r AO =1，h AA OO 212111==（h AA =1也是圆柱的高）； 第三步：勾股定理：21212O O A O OA +=⇒222)2(r hR +=⇒22)2(hr R +=，解出R例3（1）一个正六棱柱的底面上正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为89，底面周长为3，则这个球的体积为 解：设正六边形边长为a ，正六棱柱的高为h ，底面外接圆的半径为r ，则21=a ，正六棱柱的底面积为833)21(4362=⋅⋅=S ，89833===h Sh V 柱，∴3=h ，4)3(14222=+=R也可1)21()23(222=+=R ），1=R ，球的体积为34π=球V ； （2）直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===,120BAC ∠=︒，则此球的表面积等于 .解：32=BC ，4120sin 322==r ，2=r ，5=R ，π20=S ； （3）已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直，︒=∠===60,2,3AEB AD EB EA ，则多面体ABCD E -的外接球的表面积为 .π16解：折叠型，法一：EAB ∆的外接圆半径为31=r ，11=OO ，231=+=R ； 法二：231=M O ，21322==D O r ，4413432=+=R ，2=R ，π16=表S ； 法三：补形为直三棱柱，可改变直三棱柱的放置方式为立式，算法可同上，略.换一种方式，通过算圆柱的轴截面的对角线长来求球的直径：162)32()2(222=+=R ，π16=表S ； （4）在直三棱柱111C B A ABC -中，4,3,6,41====AA A AC AB π，则直三棱柱111C B A ABC -的外接球的表面积为 .π3160解：法一：282164236162=⋅⋅⋅-+=BC ，72=BC ，37423722==r ，372=r ， 3404328)2(2122=+=+=AA r R ，π3160=表S ； 法二：求圆柱的轴截面的对角线长得球直径，此略.第二讲 锥体背景的模型类型四、切瓜模型（两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法）图4-1图4-2图4-3图4-41．如图4-1，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点. 解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；（3）题第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R ；事实上，ACP ∆的外接圆就是大圆，直接用正弦定理也可求解出R .2．如图4-2，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且AC PA ⊥，则 利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=3．如图4-3，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4．题设：如图4-4，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）第一步：易知球心O 必是PAC ∆的外心，即PAC ∆的外接圆是大圆，先求出小圆的直径r AC 2=； 第二步：在PAC ∆中，可根据正弦定理R CcB b A a 2sin sin sin ===，求出R . 例4 （1）正四棱锥的顶点都在同一球面上，若该棱锥的高为1，底面边长为32，则该球的表面积为 . 解：法一：由正弦定理（用大圆求外接球直径）；法二：找球心联合勾股定理，72=R ，ππ4942==R S ；（2）正四棱锥ABCD S -的底面边长和各侧棱长都为2，各顶点都在同一球面上，则此球体积为解：方法一：找球心的位置，易知1=r ，1=h ，r h =，故球心在正方形的中心ABCD 处，1=R ，34π=V 方法二：大圆是轴截面所的外接圆，即大圆是SAC ∆的外接圆，此处特殊，SAC Rt ∆的斜边是球半径，22=R ，1=R ，34π=V . （3）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ ） A ．433 B ．33 C ．43 D ．123解：高1==R h ，底面外接圆的半径为1=R ，直径为22=R ，设底面边长为a ，则260sin 2==a R ，3=a ，433432==a S ，三棱锥的体积为4331==Sh V ； （4）在三棱锥ABC P -中，3===PC PB PA ,侧棱PA 与底面ABC 所成的角为60，则该三棱锥外接球的体积为（ ） A ．π B.3π C. 4π D.43π 解：选D ，由线面角的知识，得ABC ∆的顶点C B A ,,在以23=r 为半径的圆上，在圆锥中求解，1=R ； （5）已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =，则此棱锥的体积为（ ）AA．6 B．6 C．3 D．2解：36)33(12221=-=-=r R OO ，362=h ，62362433131=⋅⋅==Sh V 球 类型五、垂面模型（一条直线垂直于一个平面）1．题设：如图5，⊥PA 平面ABC ，求外接球半径.解题步骤：第一步：将ABC ∆画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ，连接PD ，则PD 必过球心O ； 第二步：1O 为ABC ∆的外心，所以⊥1OO 平面ABC ，算出小圆1O 的半径r D O =1（三角形的外接圆直径算法：利用正弦定理，得r C c B b A a 2sin sin sin ===），PA OO 211=； 第三步：利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=.2．题设：如图5-1至5-8这七个图形，P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的 顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）； 第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R 方法二：小圆直径参与构造大圆，用正弦定理求大圆直径得球的直径. 例5 一个几何体的三视图如图所示，则该几何体外接球的表面积为( )C A ．π3 B ．π2 C ．316πD ．以上都不对解：选C ， 法一：（勾股定理）利用球心的位置求球半径，球心在圆锥的高线上，221)3(R R =+-,32=R ,ππ31642==R S ； 法二：（大圆法求外接球直径）如图，球心在圆锥的高线上，故圆锥的轴截面三角形PMN 的外接圆是大圆，于是3460sin 22==R ，下略； 第三讲 二面角背景的模型类型六、折叠模型题设：两个全等三角形或等腰三角形拼在一起，或菱形折叠(如图6)俯视图侧视图正视图解答图图6第一步：先画出如图6所示的图形，将BCD ∆画在小圆上，找出BCD ∆和BD A '∆的外心1H 和2H ； 第二步：过1H 和2H 分别作平面BCD 和平面BD A '的垂线，两垂线的交点即为球心O ，连接OC OE ,； 第三步：解1OEH ∆，算出1OH ，在1OCH Rt ∆中，勾股定理：22121OC CH OH =+ 注：易知21,,,H E H O 四点共面且四点共圆，证略.例6（1）三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 和△ABC 均为边长为2的正三角形，则三棱锥ABC P -外接球的半径为 . 解：如图，3460sin 22221===r r ，3221==r r ，312=H O ， 35343121222=+=+=r H O R ，315=R ；法二：312=H O ，311=H O ，1=AH ， 352121222=++==O O H O AH AO R ，315=R ；（2）在直角梯形ABCD 中，CD AB //， 90=∠A ，45=∠C ，1==AD AB ，沿对角线BD 折成四面体BCD A -'，使平面⊥'BD A 平面BCD ，若四面体BCD A -'的顶点在同一个球面上，则该项球的表面积为 π4(2)题-2(2)题-1→A(3)题解：如图，易知球心在BC 的中点处，π4=表S ；（1）题（3）在四面体ABC S -中，BC AB ⊥，2==BC AB ，二面角B AC S --的余弦值为33-，则四面体ABC S -的外接球表面积为 π6 解：如图，法一：33)2cos(cos 211-=+∠=∠πO OO B SO ， 33sin 21=∠O OO ，36cos 21=∠O OO ， 22cos 21211=∠=O OO O O OO ，232112=+=R ，ππ642==R S ； 法二：延长1BO 到D 使111r BO DO ==，由余弦定理得6=SB ，2=SD ，大圆直径为62==SB R ； （4）在边长为32的菱形ABCD 中，60=∠BAD ，沿对角线BD 折成二面角C BD A --为120的四面体ABCD ，则此四面体的外接球表面积为 π28解：如图，取BD 的中点M ，ABD ∆和CBD ∆的外接圆半径为221==r r ，ABD ∆和CBD ∆的外心21,O O 到弦BD 的距离（弦心距）为121==d d ，法一：四边形21MO OO 的外接圆直径2=OM ，7=R ，π28=S ； 法二：31=OO ，7=R ；法三：作出CBD ∆的外接圆直径CE ,则3==CM AM ， 4=CE ，1=ME ，7=AE ，33=AC ，72147227167cos -=⋅⋅-+=∠AEC ，7233sin =∠AEC ，72723333sin 2==∠=AEC AC R ，7=R ；(5)在四棱锥ABCD 中， 120=∠BDA ，150=∠BDC ，2==BD AD ，3=CD ，二面角CBD A --(4)题图的平面角的大小为120，则此四面体的外接球的体积为 解：如图，过两小圆圆心作相应小圆所在平面的垂线确定球心，→抽象化(5)题解答图-2(5)题解答图-11B32=AB ，22=r ，弦心距32=M O ，13=BC ，131=r ，弦心距321=M O ，∴2121=O O ，72120sin 21==O O OM ，法一：∴292222=+==OM MD OD R ，29=R ，∴329116π=球V ； 法二：2522222=-=M O OM OO ，∴29222222=+==OO r OD R ，29=R ，∴329116π=球V . 类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7题设：如图7，90=∠=∠ACB APB ，求三棱锥ABC P -外接球半径（分析：取公共的斜边的中点O ，连接OC OP ,，则AB OP OC OB OA 21====，∴O 为三棱锥ABC P -外接球球心，然后在OCP 中求出半径），当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关，只要不是平角球半径都为定值.例7（1）在矩形ABCD 中，4=AB ，3=BC ，沿AC 将矩形ABCD 折成一个直二面角D AC B --，则四面体ABCD 的外接球的体积为（ ）A ．π12125 B ．π9125 C ．π6125 D ．π3125解：（1）52==AC R ，25=R ，6125812534343πππ=⋅==R V ，选C（2）在矩形ABCD 中，2=AB ，3=BC ，沿BD 将矩形ABCD 折叠，连接AC ，所得三棱锥BCDA -的外接球的表面积为 ．解：BD 的中点是球心O ，132==BD R ，ππ1342==R S .第四讲 多面体的内切球问题模型类型八、锥体的内切球问题1．题设：如图8-1，三棱锥ABC P -上正三棱锥，求其内切球的半径. 第一步：先现出内切球的截面图，H E ,分别是两个三角形的外心；第二步：求BD DH 31=，r PH PO -=，PD 是侧面ABP ∆的高； 第三步：由POE ∆相似于PDH ∆，建立等式：PDPODH OE =，解出r 2．题设：如图8-2，四棱锥ABC P -是正四棱锥，求其内切球的半径第一步：先现出内切球的截面图，H O P ,,三点共线；第二步：求BC FH 21=，r PH PO -=，PF 是侧面PCD ∆的高；第三步：由POG ∆相似于PFH ∆，建立等式：PFPOHF OG =，解出3．题设：三棱锥ABC P -是任意三棱锥，求其的内切球半径方法：等体积法，即内切球球心与四个面构成的四个三棱锥的体积之和相等 第一步：先画出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r ，建立等式：PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步：解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3例8 （1）棱长为a 的正四面体的内切球表面积是62a π，解：设正四面体内切球的半径为r ，将正四面体放入棱长为2a的正方体中（即补形为正方体），如图，则 2622313133aa V V ABC P =⋅==-正方体， 又 r a r a Sr V ABC P 223343314314=⋅⋅⋅=⋅=-， ∴263332a r a =，62a r =，∴内切球的表面积为(1)题D图8-1A图8-26422a r S ππ==表（注：还有别的方法，此略）（2）正四棱锥ABCD S -的底面边长为2，侧棱长为37解：如图，正四棱锥ABCD S -的高7=h ，正四棱锥ABCD S -的体积为374=-ABCD S V 侧面斜高221=h ，正四棱锥ABCD S -的表面积为284+=表S ，正四棱锥ABCD S -的体积为r r S V ABCD S ⋅+==-328431表，∴3743284=⋅+r ， 771427)122(7221728474-=-=+=+=r （3）三棱锥ABC P -中，底面ABC ∆是边长为2的正三角形，⊥PA 底面ABC ，2=PA ，则32解：如图，3=∆ABC S ，2==∆∆ACP ABP S S ，7=∆BCP S ，743++=表S ，三棱锥ABC P -的体积为332=-ABC P V ， 另一表达体积的方式是r r S V ABC P ⋅++==-347331表，∴3323473=⋅++r ，∴47332++=r习题： 1．若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（ ） A.3 B.6 C.36 D.9 解：【A 】616164)2(2=++=R ，3=R【三棱锥有一侧棱垂直于底面，且底面是直角三角形】【共两种】2． 三棱锥ABC S -中，侧棱⊥SA 平面ABC ，底面ABC 是边长为3的正三角形，32=SA ，则该三棱锥的外接球体积等于 .332π(2)题(3)题B解：260sin 32==r ，16124)2(2=+=R ，42=R ，2=R ，外接球体积332834ππ=⋅ 【外心法（加中垂线）找球心；正弦定理求球小圆半径】3．正三棱锥ABC S -中，底面ABC 是边长为3的正三角形，侧棱长为2，则该三棱锥的外接球体积等于 .解：ABC ∆外接圆的半径为 ，三棱锥ABC S -的直径为3460sin 22== R ，外接球半径32=R ， 或1)3(22+-=R R ，32=R ，外接球体积2733233834343πππ=⋅==R V ， 4．三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 边长为2的正三角形，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .解：PAC ∆的外接圆是大圆，3460sin 22==R ，32=R ， 5． 三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，3==PC PA ，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .解：973324992cos 222=⋅⋅-+=⋅-+=∠PC PA AC PC PA P ，81216)97(1sin 22⋅=-=∠P ，924sin =∠P ，42922992422===R ，829=R 6． 三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，PC PA ⊥，BC AB ⊥，则三棱锥ABCP -外接球的半径为 .解：AC 是公共的斜边，AC 的中点是球心O ，球半径为1=R。

立体几何中内切球和外接球问题题目：探索立体几何中的内切球和外接球问题在立体几何中，内切球和外接球问题是一个引人深思的话题。

通过对这个主题的深入探讨，我们可以更好地理解立体几何的原理和性质。

本文将围绕内切球和外接球问题展开讨论，从基本概念到数学推导，深入剖析这一有趣而重要的话题。

1. 内切球和外接球的定义在立体几何中，内切球和外接球分别是指一个球体在一个立体图形内部与其接触，以及一个球体在一个立体图形外部与其接触。

这两个概念可以应用在各种几何图形中，如圆柱体、圆锥体甚至更为复杂的多面体。

内切球和外接球不仅在几何形状中具有重要意义，还在工程学、艺术设计等领域有着广泛的应用价值。

2. 内切球和外接球的性质内切球和外接球在几何中具有许多有趣的性质。

内切球和外接球的半径之比有一定的规律，可以通过数学推导得出。

内切球和外接球的位置关系也有一定的特点，可以通过几何推理进行证明。

这些性质的深入理解有助于我们更好地应用立体几何知识解决实际问题。

3. 内切球和外接球的数学推导从数学角度来看，内切球和外接球问题涉及到许多重要的数学定理和方法。

通过数学推导，我们可以得到内切球和外接球的半径之比、位置关系等具体数学表达式。

这些推导过程需要运用到圆、球体的性质，以及立体几何的相关知识，是一个不可或缺的数学推理过程。

4. 个人观点和理解在我看来，内切球和外接球问题是立体几何中的一个精彩而复杂的主题。

通过对这个问题的探讨，我深刻地感受到数学的美妙和奥妙。

数学不仅是一门实用的科学，更是一个充满乐趣和挑战的学科。

通过不断地学习和探索，我们可以更好地理解立体几何的原理和应用，为我们的工程、设计和科学研究提供有力的支持。

内切球和外接球问题是立体几何中的一个重要而有趣的话题。

通过深入探讨这个主题，我们可以更好地理解立体几何的原理和应用，为我们的学习和工作带来更多的乐趣和启发。

希望本文的内容能够对您有所帮助，也希望您能够对立体几何有着更深入的理解和探索。

立体几何中的外接球内切球棱切球问题1. 概述在立体几何中，外接球、内切球和棱切球是常见的几何问题。

它们在工程、建筑、数学等领域都有重要的应用。

本文将围绕外接球、内切球和棱切球展开讨论，探究它们的性质和相关问题。

2. 外接球的定义和性质外接球是指一个球与一个或多个其他物体外接，外接球的半径等于所外接物体相应部分的长度，在立体几何中有着重要的应用。

外接球的性质1）外接球的圆心在被外接物体向外伸出的法线上。

2）外接球的半径等于被外接物体的相应部分的长度。

3）对于凸体而言，外接球存在且唯一。

3. 内切球的定义和性质内切球是指一个球恰好与另一个物体相切，内切球在立体几何中也有着重要的应用。

内切球的性质1）内切球的圆心在被内切物体向内伸出的法线上。

2）对于凸体而言，内切球存在且唯一。

3）内切球在不同物体中的位置可能不同，但其存在性是唯一的。

4. 棱切球的定义和性质棱切球是指一个球与多个物体之间棱切的情况，在立体几何中也有着重要的应用。

棱切球的性质1）棱切球的圆心在被棱切物体所在的平面上。

2）对于凸体而言，棱切球存在且唯一。

3）棱切球在不同物体中的位置可能不同，但其存在性是唯一的。

5. 实际应用举例外接、内切和棱切球在实际应用中有着广泛的应用。

比如在建筑工程中，常常需要计算建筑物的外接球、内切球和棱切球，以确定其结构和稳定性。

在数学建模中，外接、内切和棱切球也常常出现，用于解决各种数学问题。

6. 结论外接球、内切球和棱切球是立体几何中重要的概念，它们的性质和应用涉及到广泛的领域。

对这些几何问题的深入研究和应用可以帮助我们更好地理解立体几何的性质，并且为实际问题的解决提供理论支持。

希望本文能够帮助读者更好地理解外接球、内切球和棱切球的相关问题，并且激发更多人对立体几何的兴趣和研究。

外接球、内切球和棱切球作为立体几何中的重要概念，其性质和应用不仅仅局限于几何学。

它们的相关问题还涉及到数学建模、工程设计、建筑结构等领域，对于实际问题的解决提供了理论支持和指导。

A. 4 3
27
D
B. 6
2
C
C. 6 8
D. 6 24
P
A
E
B
D
C
E
图3
2、构造长方体 已知A点B A、6,BA、C=C2、1D3在,A同D一=8个，球则面B上、，CA两B点间平的面A 球BC面D距离B是C 34DC.
O
B C
D 图 5
三、确定球心位置法
在矩形ABCD中，AB=4，BC=3，AC沿将矩形
正四面体的体积
S表
4
3 a2 4
3a 2
1 3
S表
r
VABCD
V A BCD
1 3
3 a 2 AE 3 a 2
4
12
r 3VABCD
3 2 a3 12
6a
S表
3a 2 12
AB 2 BE 2
图1
3 a2 12
a2 Βιβλιοθήκη 3 3a22 a3 12
RtBEO
在得 中得， 即 ， R 6 a
② S球面 4 R2
图3
图4
定义1：若一个多面体的各顶点都在一个球的球图面5 上，
则称这个多面体是这个球的内接多面体，
这个球是这个 多面体的外接球 。
定义2：若一个多面体的各面都与一个球的球面相切，
则称这个多面体是这个球的外切多面体，
这个球是这个 多面体的内切球 。
棱切： 一个几何体各个面分别与另一个几 何体各条棱相切。
D
C
解
设正四棱锥的底面中心为 O1 ，外接球的球
O1 A 图3 B
心为O，如图3所示.∴由球的截面的性质， 2
可得 OO1 平面ABCD

立体几何中的外接球与内切球问题在我们的数学学习中，立体几何是非常重要的一部分。

在立体几何学习中，我们不仅需要掌握各种图形的形状和性质，也需要深入了解这些图形中的各种关系。

其中外接球和内切球是两个非常重要的概念，在立体几何中被广泛使用。

一、外接球外接球是指和一个多面体的所有顶点都相切的球。

在三维空间中，一个正四面体的外接球，就是四面体的四个顶点构成的球。

同理，其他多面体都有一组外接球。

外接球的性质可以帮助我们计算多面体的各种数据。

对于正四面体而言，我们可以得知，外接球的半径和棱长之间的关系为：外接球的半径等于正四面体棱长的一半。

这个特点可以应用于其他多面体中，为我们计算多面体提供更多帮助。

二、内切球内切球是指可以被一个多面体的所有面都切到的球。

在三维空间中，一个正四面体的内切球，就是以正四面体的每个面为切面所构成的球。

同理，其他多面体都有一组内切球。

内切球的性质可以帮助我们更好地了解多面体的各种性质。

对于正四面体而言，我们可以得知，内切球的半径和棱长之间的关系为：内切球的半径等于正四面体棱长的三分之一。

通过内切球的特点，我们可以更好地了解多面体的横截面形状，深入了解多面体的性质。

三、外接球与内切球的应用外接球和内切球在数学学科中非常重要。

在生活中，我们可以看到不少与这两个概念有关的例子。

例如，在搭建玩具拼图时，我们可以注意到玩具拼图中各个构件的外接球和内切球的关系。

同样的，建筑设计和工程规划中也常常涉及到多面体的外接球和内切球问题。

此外，街头艺术品和雕塑等艺术作品中也常常出现多面体和其相应的外接球或内切球。

总之，立体几何中的外接球和内切球是我们不能忽视的重要概念。

它们不仅仅是数学学科中的知识点，也与我们日常生活中的许多方面有着密不可分的关系。

因此，我们应该更加深入了解这两个概念，并将其应用在我们的学习和生活中，从而更好地了解和利用立体几何的基础知识。

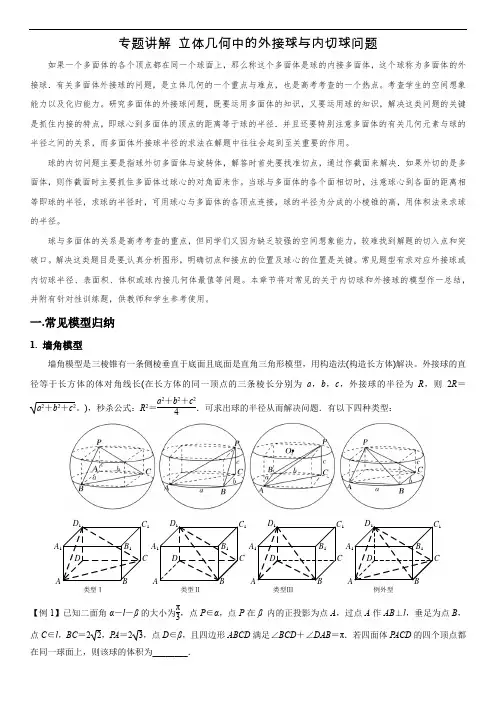
专题讲解立体几何中的外接球与内切球问题如果一个多面体的各个顶点都在同一个球面上，那么称这个多面体是球的内接多面体，这个球称为多面体的外接球．有关多面体外接球的问题，是立体几何的一个重点与难点，也是高考考查的一个热点。

考查学生的空间想象能力以及化归能力。

研究多面体的外接球问题，既要运用多面体的知识，又要运用球的知识，解决这类问题的关键是抓住内接的特点，即球心到多面体的顶点的距离等于球的半径．并且还要特别注意多面体的有关几何元素与球的半径之间的关系，而多面体外接球半径的求法在解题中往往会起到至关重要的作用。

球的内切问题主要是指球外切多面体与旋转体，解答时首先要找准切点，通过作截面来解决．如果外切的是多面体，则作截面时主要抓住多面体过球心的对角面来作。

当球与多面体的各个面相切时，注意球心到各面的距离相等即球的半径，求球的半径时，可用球心与多面体的各顶点连接，球的半径为分成的小棱锥的高，用体积法来求球的半径。

球与多面体的关系是高考考查的重点，但同学们又因为缺乏较强的空间想象能力，较难找到解题的切入点和突破口。

解决这类题目是要认真分析图形，明确切点和接点的位置及球心的位置是关键。

常见题型有求对应外接球或内切球半径、表面积、体积或球内接几何体最值等问题。

本章节将对常见的关于内切球和外接球的模型作一总结，并附有针对性训练题，供教师和学生参考使用。

一.常见模型归纳1. 墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型，用构造法(构造长方体)解决。

外接球的直径等于长方体的体对角线长(在长方体的同一顶点的三条棱长分别为a，b，c，外接球的半径为R，则2R＝a 2＋b2＋c2。

)，秒杀公式：R2＝a2＋b2＋c24．可求出球的半径从而解决问题．有以下四种类型：【例1】已知二面角α－l－β的大小为π3，点P∈α，点P在β内的正投影为点A，过点A作AB⊥l，垂足为点B，点C∈l，BC＝22，P A＝23，点D∈β，且四边形ABCD满足∠BCD＋∠DAB＝π．若四面体P ACD的四个顶点都在同一球面上，则该球的体积为________．A BCDA1B1C1D1类型ⅠA BCDA1B1C1D1类型ⅡA BCDA1B1C1D1类型ⅢA BCDA1B1C1D1例外型【例2】已知三棱锥P －ABC 的四个顶点在球O 的球面上，P A ＝PB ＝PC ，△ABC 是边长为2的正三角形，E ，F 分别是P A ，AB 的中点，∠CEF =90°，则球O 的体积为( )．A ．68πB ．64πC ．62πD ．6π【变式练习1】在空间直角坐标系Oxyz 中，四面体ABCD 各顶点的坐标分别为A (2，2，1)，B (2，2，－1)，C (0，2， 1)，D (0，0，1)，则该四面体外接球的表面积是( )A ．16πB ．12πC ．43πD ．6π【变式练习2】在长方体ABCD －A 1B 1C 1D 1中，底面ABCD 是边长为32的正方形，AA 1＝3，E 是线段A 1B 1上一点， 若二面角A －BD －E 的正切值为3，则三棱锥A －A 1D 1E 外接球的表面积为________．2. 对棱相等模型对棱相等模型是三棱锥的三组对棱长分别相等模型，用构造法(构造长方体)解决。

几何体的外接球与内切球的有关问题一、外接球的问题简单多面体外接球问题是立体几何中的难点和重要的考点，此类问题实质是计算球的半径或确定球心O 的位置问题，其中球心的确定是关键． （一） 由球的定义确定球心球的定义：在空间中，如果一个定点与一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体的外接球的球心．由上述性质，可以得到确定简单多面体外接球的球心的如下结论． 结论1：正方体或长方体的外接球的球心其体对角线的中点．结论2：正棱柱的外接球的球心是上下底面中心的连线的中点．结论3：直三棱柱的外接球的球心是上下底面三角形外心的连线的中点，由球心、底面中心及底面一顶点构成的直角三角形便可得球半径.（在1BOO Rt ∆中，21212OO BO BO +=，即222)2(h r R +=.）结论4：正棱锥的外接球的球心在其高上，具体位置可通过构造直角三角形利用勾股定理求得． （以正三棱锥为例：设正三棱锥的底面△ABC 的边长为a ，高为h ，外接球球心为O ，半径为R .在1AOO Rt ∆中，21212OO AO AO +=，即222)(33R h a R -+⎪⎪⎭⎫⎝⎛=.）结论5：若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心，则公共斜32R a=2222a b c R ++=BC边的一半就是其外接球的半径．（二）构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处． 1.可构造正方体的类型：①正四面体：棱长对应正方体的面对角线.① ② ③②三条侧棱两两垂直的正三棱锥：底面棱长对应正方体的面对角线，侧棱对应正方体的棱长. ③四个面都是是直角三角形的三棱锥：最长的棱长对应正方体的体对角线. 2.可构造长方体和正方体的类型①同一个顶点上的三条棱两两垂直的四面体；②三个侧面两两垂直的三棱锥；③有三个面是直角三角形的三棱锥；①与②与③ ④④相对的棱相等的三棱锥：设对应长方体的长、宽、高分别为a 、b 、c ，则BC 2=a 2+b 2，AC 2=a 2+c 2，AB 2=b 2+c 2. 所以对应长方体的体对角线为2222222AB AC BC c b a ++=++.⑤含有其它线面垂直关系的棱锥. （三） 由性质确定球心利用球心O 与截面圆圆心O’的连线垂直于截面圆，确定球心． 记球的半径为R ，截面圆的半径为r ，球心O 与截面圆圆心O’A BCDABCPABCP的距离为d，则有R2=r2+d 2.（四） 圆柱外接球模型计算球的半径一个底面半径为r ，高为h 的圆柱，求它的外接球半径. 222)2(h r R +=（1） （2） （3）变形一：如果我们对圆柱上下底面对应位置处，取相同数量的点，比如都取三个点，如图（1）所示.我们可以得到（直）三棱柱，它的外接球其实就是这个圆柱的外接球，所以说直棱柱的外接球求半径符合这个模型. 在这里棱柱的高就是公式中的h ，而棱柱底面△ABC 外接圆的半径则是公式中的r .变形二：如果把三棱柱上面的C 1去掉，如图（2）所示，我们得到有一个侧面⊥矩形底面的四棱锥，其中r 为垂直底面的侧面△ABC 的外接圆半径，h 为垂直于那个侧面的底面边长AA 1.变形三：如果把上面的那个三棱柱上面的B 1,C 1两点去掉，如图（3）所示，我们得到一根侧棱⊥底面的三棱锥，其中r 为底面△ABC 外接圆半径，h 为垂直于底面的那条侧棱AA 1.二、内切球问题若一个多面体的各面都与一个球的球面相切， 则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球.结论1：内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等. 结论2：正多面体的内切球和外接球的球心重合.结论3：正棱锥的内切球和外接球球心都在高线上，但不重合. 结论4：基本方法：构造三角形利用相似比和勾股定理. 结论5：体积分割是求内切球半径的通用做法. （一）正方体的的内切球设正方体的棱长为a ，求（1）内切球半径；（2）与棱相切的球半径.Rr2h A BC1A 1B 1C A BC1A 1B A BC1A（1）内切球：截面图为正方形的内切圆，得2a R =. （2）棱切球：切点为正方体各棱的中点，截面图为为正方形的外接圆，得22a R =. （二）棱锥的内切球(分割法)将内切球的球心与棱锥的各个顶点连线，将棱锥分割成以原棱锥的面为底面，内切球的半径为高的小棱锥，根据分割前后的体积相等，列出关于半径的方程.设三棱锥的棱长为a ，内切球半径为r.V V V V VPAB O PBC O PAC O ABC O ABCP -----+++=r S r S r S r S PAB PBC PAC ABC 31313131+++= r S S S S PAB PBC PAC ABC )(31+++= 内切球r S ABC P -=31所以ABCP ABCP S V r --=3内切球一般地，记棱锥的体积为V ，表面积为S ，则内切球的半径为SV r 3=. （三）圆柱、圆锥的内切球(截面法)（1）圆柱的内切球：圆柱的轴截面为正方形，记圆柱的底面圆的半径r ，内切球的半径R ，则R =r . （2）圆锥的内切球：圆锥的轴截面为三角形的内切圆，记圆锥的底面圆的半径r ，内切球的半径R ，由于在△ABC 中，所以CS R 2=.备注：1.三角形内切圆的半径S S S S AOBAOC BOC ABC ∆∆∆∆++=r c b a cr br ar )(21212121++=++= 内切圆r C ABC ∆=21所以三角形内切圆的半径为CSr 2=，其中S 为△ABC 的面积，C 为△ABC 的周长. 2. 三角形外接圆的半径利用正弦定理R C c B b A a 2sin sin sin ===，C cB b A a R sin 2sin 2sin 2===. ①正三角形：a a R 3360sin 2=︒=，其中a 为正三角形的边长.②直角三角形：290sin 2cc R =︒=，其中c 为直角三角形的斜边.3. 正三角形的内切圆与外接圆的半径之比正三角形的内切圆与外接圆的两个圆心“二心合一”. 设正三角形的边长为a ，内切圆半径为r ，外接圆半径为R.由于a a R 3360sin 2=︒=，a a a a a a C S r 6360sin 2122=++︒⋅⋅⋅⨯==， 所以1:2:=r R ，即圆心O 为正三角形高h 的三等分点.4. 正四面体的内切球与外接球的半径之比正四面体的内切球与外接球的两个球心“二心合一”. 设正四面体A-BCD 的棱长为a ，内切球半径为r ，外接球 半径为R ，则OA=OB=R ，OE=r.∵底面△BCD 为正三角形，∴BE=a 33 在BEO Rt ∆中，222OE BE BO +=，即22233r a R +⎪⎪⎭⎫ ⎝⎛=，得a R 46= ∴1:3:=r R ，即球心O 为正四面体高h 的四等分点. 5.正三棱柱的内切球与外接球的半径之比正三棱柱的内切球与外接球的球心是重合的，过侧棱1AA 和它们的球心O 作截面如下图所示：设正三棱柱底面边长为a . 由于内切球投影到底面的圆是底面正三角形的内切圆，所以a R 632=，从而正三棱柱的高为a R h 3322==. 在O D A Rt 11∆中，得22222211211256333a a a R D A R =⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=，a R 1251=∴因此1:5:21=R R .。

求它的外接球的半径.
设计意图：球心是决定球的位置关键点，利用球心到正三棱锥 四个顶点的距离相等且为球半径，找到球心在高线上 ，以球心 的位置特点来抓球的基本量，这是解决球有关问题常用的方 法．
变式1：正四棱锥S-ABC的底面边长2,侧棱长都 为 ，点S、A、B、C都在同一球面上，求此球 的体积.
设计意图：选择最佳角度找出含有正棱锥特征元素的外接球的 球心，本题提供的这种思路是探求正棱锥外接球半径的通解通 法，该方法的实质就是通过寻找外接球的一个轴截面圆，把空 间问题转化成平面问题，这种等价转化的数学思想方法值得我 们学习.
第四环节: 深入探究，加强理解
变式2:三棱柱 的底面是边长为2的等边三角形， 侧棱垂直底面，侧棱长为3，求该三棱柱的外 接球半径. 变式3:若是正五棱柱、正六棱柱如何确定外接 球球心的位置？
设计意图: 设计意图：让学生学会直棱柱的外接球可 利用棱柱的上下底面平行，借助球的对称性，球心为 上下底面外接圆的圆心连线的中点，再根据勾股定理 求球的半径.变式练习由易到难,循序渐进, 考察对方法 的灵活应用，找到通法.
第七环节 布置作业
1.已知三棱锥D﹣ABC中，AB=BC=1，AD=2，BD= ， AC= ，BC⊥AD，求三棱锥的外接球的表面积.
2.在三棱椎A﹣BCD中，侧棱AB，AC，AD两两垂直， △ABC，△ACD，△ADB的面积分别为 ， ， ， 求该三棱椎外接球的表面积.
3.四面体PABC中PA=BC=2,AB=PC=4,,AC=PB= ，求其 外接球的体积.
由于学生没有完整的学习完空间点、线、面的位 置关系，只是对一些空间几何体有了初步的认识，这 对这节课学生的探索发现有所影响.
三. 教学目标分析
1.知识与技能目标 熟练球的性质，掌握求空间几何体外接球半径的

第二讲 几何体的外接球和内切球问题※基础知识：1．常见平面图形：正方形，长方形，正三角形的外接圆和内切圆长方形（正方形）的外接圆半径为对角线长的一半，正方形的内切圆半径为边长的一半；正三角形的内切圆半径：6a外接圆半径：3a 三角形面积：24正三角形三心合一，三线合一，心把高分为2:1两部分。

2．球的概念：概念1：与定点距离等于或小于定长的点的集合，叫做球体，简称球.，定长叫球的半径；与定点距离等于定长的点的集合叫做球面.一个球或球面用表示它的球心的字母表示，例如球O 或O ．概念2：半圆以它的直径为旋转轴，旋转所成的曲面叫做球面，球面所围成的几何体叫做球体，简称球。

3．球的截面：用一平面α去截一个球O ，设OO '是平面α的垂线段，O'为垂足，且OO d '=，所得的截面是以球心在截面内的射影为圆心，以r .球面被经过球心的平面截得的圆叫做大圆，被不经过球心的平面截得的圆叫做小圆.4．空间几何体外接球、内切球的概念： 定义1：若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球。

定义2：若一个多面体的各面都与一个球的球面相切， 则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球。

长方体的外接球 正方体的内切球5．外接球和内切球性质：（1）内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等。

（2）正多面体的内切球和外接球的球心重合。

（3）正棱锥的内切球和外接球球心都在高线上，但不重合。

（4）基本方法：构造三角形利用相似比和勾股定理。

（5）体积分割是求内切球半径的通用做法。

长方体的外接球半径公式：2222c b a R ++=，其中,,a b c 分别为长方体共顶点的3条棱长正棱锥的外接球半径公式：2,2a R h= 2侧棱=2R h ⋅外正棱锥，其中a 为侧棱长，h 为正棱锥的高正棱柱的外接球球心在两底面中心连线的中点处。

内切与外接1 球与柱体1.1 球与正方体例 1 棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E F ，分别是棱1AA ，1DD 的中点，则直线EF 被球O 截得的线段长为（ ）A ．22B ．1C ．212+D 21.2 球与长方体长方体各顶点可在一个球面上，故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,,a b c 其体对角线为l .当球为长方体的外接球时，截面图为长方体的对角面和其外接圆，和正方体的外接球的道理是一样的，故球的半径2222l a b c R ++== 例 2 在长、宽、高分别为2，2，4的长方体内有一个半径为1的球，任意摆动此长方体，则球经过的空间部分的体积为( )A.10π3B.4πC.8π3D.7π31.3 球与正棱柱例3 正四棱柱1111ABCD A B C D -的各顶点都在半径为R 的球面上，则正四棱柱的侧面积有最 值，为 .2 球与锥体 规则的锥体，如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱锥的棱和高产生联系，然后考查几何体的体积或者表面积等相关问题.2.1 球与正四面体2222233a R r a R r CE +=-=，=，解得：66,.R r ==例4 将半径都为１的四个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最 小值为 ( ) A.3263+ B. 2+263 C. 4+263 D. 43263+2.2 球与三条侧棱互相垂直的三棱锥例5 在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且AM MN ⊥,若侧棱 23SA =,则正三棱锥S-ABC 外接球的表面积是______2.3 球与正棱锥球与正棱锥的组合，常见的有两类，一是球为三棱锥的外接球，此时三棱锥的各个顶点在球面上，根据截面图的特点，可以构造直角三角形进行求解.二是球为正棱锥的内切球，例如正三棱锥的内切球，球与正三棱锥四个面相切，球心到四个面的距离相等，都为球半径R ．这样求球的半径可转化为球球心到三棱锥面的距离，故可采用等体积法解决，即四个小三棱锥的体积和为正三棱锥的体积.例6 在三棱锥P －ABC 中，PA ＝3侧棱PA 与底面ABC 所成的角为60°，则该三棱锥外接球的体积为（ ）A ．π B.3π C. 4π D.43π 接球的球心,则2SC R =. 例7 矩形ABCD 中，4,3,AB BC ==沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积是( )A.π12125B.π9125C.π6125D.π3125 3 球与球对多个小球结合在一起，组合成复杂的几何体问题，要求有丰富的空间想象能力，解决本类问题需掌握恰当的处理手段，如准确确定各个小球的球心的位置关系，或者巧借截面图等方法，将空间问题转化平面问题求解.例7 在半径为R 的球内放入大小相等的4个小球，则小球半径r 的最大值为（ ）4 球与几何体的各条棱相切球与几何体的各条棱相切问题，关键要抓住棱与球相切的几何性质，达到明确球心的位 置为目的，然后通过构造直角三角形进行转换和求解.例：与正四面体各棱都相切的球的半径为棱的一半：.例8 把一个皮球放入如图10所示的由8根长均为20 cm 的铁丝接成的四篇一：程序员实习总结范文以前在校很少自己做程序,对软件工程更是一无所知.来到公司,开始接触大规模(其实现在看来实习的项目其实还是很小的)软件开发,一时真的有些迷茫.比起VSS,MVC,QA,CMMI,我对JAVA,JSP,XML的一窍不通根本不值一提.大家都不想输在起点,所以都默契地在加班,这样一直持续了实习的两个月.刚来的时候始业教育显得慢吞吞,我们还经常盘算去哪哪玩之类的.我和FLYSKY(20个新生里唯一一个南区的兄弟,软件学院的)还经常出去吃各种小吃,每到一处都尝尝本地的风味,这是他的习惯.之后开始的培训还不是很难过,JAVA,C++,ORACLE,老师们讲的很好,可以说是非常好,好得我们没有几个人能听懂.大家开始发愁,我也是每天晚上都基本看书到10点.我心说得亏哥们我还练过,来之前的2月份我就自己买了一本THINKING IN JAVA,看懂看不懂怎么说也算是准备了一下JAVA.C++虽说没去上过课,但凭我的直觉我就一下看中这东西很有用,自己也看过一阵.至于ORACLE,虽然不了解,但毕竟因为佩服云飞扬的性格和敬业精神,咱SQL选修也不是白混的.专业倒还有点基础,再加上咱这自学能力也不是吹的,基本维持.可等到后来的日语课就全迷糊了:本就没有语言天赋,再加上记忆严重欠缺,总是特别害怕去上日语课.不过特别喜欢那个老师说话的感觉,加上她一直对我都很好,所以还是很用心的学着.随着培训的收尾,我们开始正式进入项目.从需求分析,概要设计到详细设计,我们一步一步的开始接触软件开发的每个细节.最受不了的就是每天都要记周报,填写自己的劳动成果.因为这个我还被QA通报了好几次呢,真的很郁闷.其实现在我很感谢这种制度化的东西,某些情况下好习惯的养成是要靠强制来确保的.详细设计之后就是企盼已久的编码,我心想终于可以做点正事了.现在回头一看才知道,其实编码只占软件开发的整个过程劳动量的1/4左右,而且其他的环节也不是想象中的那么无足轻重.编码我其实做的很不好,主要是因为需求分析阶段就没有认真仔细的理解需求和规格说明,加上编码时一个关键时段我回校和老同学叙旧.那阵项目经理(PM)就经常和我们说,有问题自己想办法,不要经常问我.PM其实是在叫我们自己酝酿,遇到难题只有憋一憋才能有真的收获.而我不在的那三天正好是大家技术/思路上的一个跃迁,很多难题的解决方法都基本成熟,大家的编码也接近50%了,所以回来时我感觉已经掉队很多.再一个就是编码中期时机器出问题,环境搭不上了,这使我更加紧张和急躁,大大影响了我的士气.后来利用五一其间的加班我终于赶完了自己的模块,达到了第一个里程碑.其实从发现落后到加班赶完这段经历,对我来说也具有里程碑的意义.不仅考验了我自己的能力和心理素质,也证明了我对集体的责任感和合作意识.我可以叫别人来帮我做赶上进度,但那样我会错过自己学习的机会,以后再遇到难题我还是不行;我也可以硬着头皮导致项目延期,那样我以后的日子保证不好过,而且这么做也不符合我的性格.事实证明我顶住压力独立完成任务不管是对集体还是对我个人都是一件大好事.紧张的编码之后是单体测试,很多人都在继续编码,原来大家的编码都是没有完全做完.本是自己给自己挑毛病的过程,我们却都用来完成之前没有完成的任务,说来不禁可笑.。