金尚年马永利理论力学第一章~全部习题答案
- 格式:pdf
- 大小:201.21 KB
- 文档页数:18
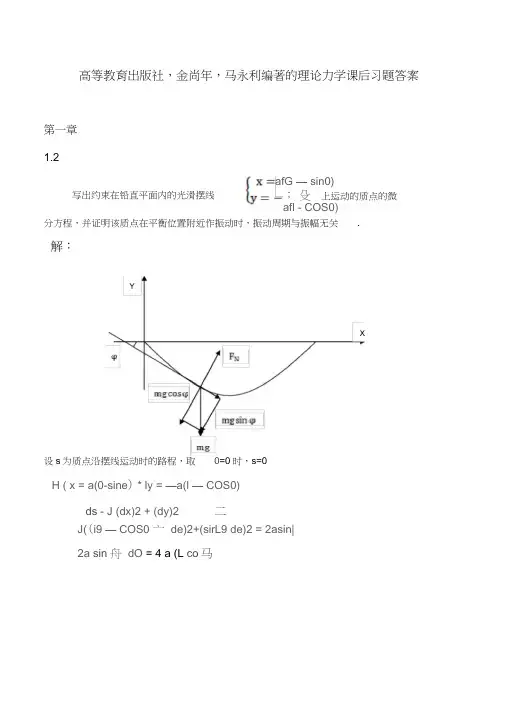
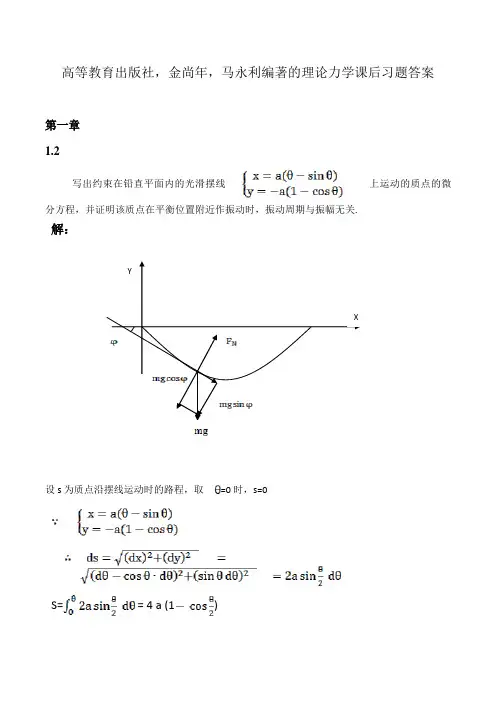
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案第一章1.2afG — sin0);殳上运动的质点的微写出约束在铅直平面内的光滑摆线afl - COS0)分方程,并证明该质点在平衡位置附近作振动时,振动周期与振幅无关.解:设s为质点沿摆线运动时的路程,取0=0时,s=0H ( x = a(0-sine) * ly = —a(l — COS0)ds - J (dx)2 + (dy)2 二J((i9 — COS0 亠de)2+(sirL9 de)2 = 2asin|2a sin舟dO = 4 a (L co 马ee As=2acos^59 + 2asin?9 = acos| 9^ + 2a sin? 9x轴的夹角,取逆时针为正,tan (p即切线斜率设(P为质点所在摆线位置处切线方向与dy cos 0 -1 tan <p =—=———〒dx sin 01聶siin<p = -cosI受力分析得:ms = —mg sin (p = mg cos-0 •・B・r a贝U2a sin二6 + a cos二6' = geos-,此即为质点的运动微分方程。
S = =(S = 4a)-(S 二4a) + —(s = 4a) =4a—周期性变化的函数,周期T=2TT产P e 该质点在平衡位置附近作振动时,振动周期与振幅无关,为2讥启.1.3证明:设一质量为m的小球做任一角度日0的单摆运动运动微分方程为m(2 + 2「日)=F gmrO = mg sin £给式两边同时乘以d9 r日d£=gsind8对上式两边关于6积分得护jgcog + c利用初始条件日=日0时日=0故c = -gcos£0由可解得0 =-{2& • J c 0 s-c 0 8o上式可化为-岸•J cos。
-cosgd日=dt两边同时积分可得 评J ; J co £o 页迅咼.1卑匸萼严进-步化简可得t 辟 J 站n r由于上面算的过程只占整个周期的1/4故由 s in 2/sin ¥=s z 两边分别对6 3微分可得cos % =s 碍C 。
第一章静力学公理和物体的受力分析一、选择题与填空题1.C2.ACD3.A, B两处约束力的方向如图所示60°第二章平面力系一、选择题与填空题■1. B; D。
2. B。
3. F;向上。
4. B。
5. 4^M;方向与水平线成60角,指向 23L右下。
6. 10kN; 10kN ; 5kN; 5kN。
7. 100kN;水平向右。
二•计算题1. F B - -70 KN F AX =70 KN ,F Ay =120 KN , M A二-30KN m2. F AX - -qa F BX二 F qa F Ay =qa F F By 二 qa - F3. F= -5kN F Dy = 4.33kN F E-4.33kN F C =24.41kND xF B^ -17.08kN F AX=F BX = -5kN l^y = -14.08kN M A=T4.66kN mF AX =10N FAy =20N M A =15N mF CD =14.1N6F Ax=2.5kN F Ay=—2.16kN M A=」kN ,m F c =20.33kN7 F B=40kNF AX = —10kNFA ^-20kN M -50kN m F cx = 40kNF ey = 0F HX =300N F Hy =100N第三章空间力系少2(-8. F A ^ = -100N F Ay 二-300N F Ex 二-300N F Ey =100N F °y 二 200N整=一一A > X Y m 一:J E £c X一、选择题与填空题f—- - Fa 6 Fa 1.B。
2.B。
3. M x(F)=O ; M y(F) —H2 44.F x=-40.2N; F y=30-2N; M z=240.2 N m。
5.F z= F sin :;F y= F cos :cos :;M x(F)二 F(ccos'cos : bsin )。

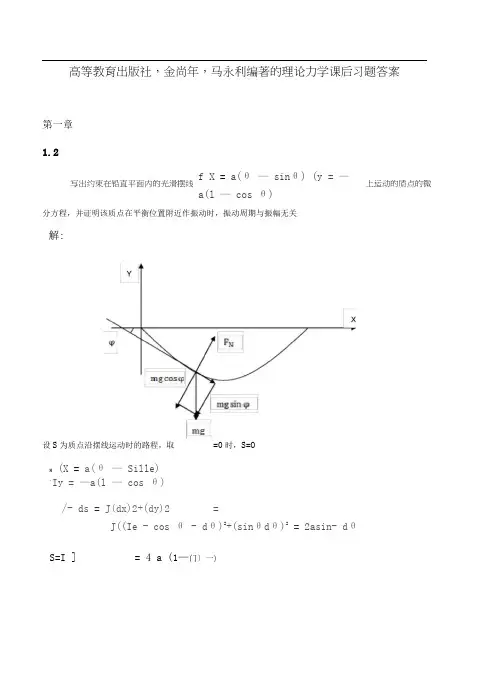
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案第一章1.2f X = a(θ — sinθ) (y = —a(l — cos θ)分方程,并证明该质点在平衡位置附近作振动时,振动周期与振幅无关解:设S 为质点沿摆线运动时的路程,取=0时,S=OH (X = a(θ — Sille) ,Iy = —a(l — cos θ) /- ds = J(dx)2+(dy)2=J((Ie - cos θ - dθ)2+(sinθdθ)2= 2asin- dθS=I ]= 4 a (1—门〕一)写出约束在铅直平面内的光滑摆线上运动的质点的微S = 2acosθ-θ + 2asiιι-θ = a cos - θ2+ 2a Sin-θ2 2 2 2 2设:为质点所在摆线位置处切线方向与 X 轴的夹角,取逆时针为正,L 二弔即切线斜率dy COS θ -1tan φ = — = ——dx sιnθ受力分析得:InS = —mg sin φ = mg cos yΩ .. Ω . - Ω 则1 ' : . 一,此即为质点的运动微分方程。
2 2 t52S =鲁(S — 4a)Λ (S - 4a) + ~(β — 4a) = 01.3证明:设一质量为m 的小球做任一角度Λ的单摆运动运动微分方程为m(L ∙2L )=F ,mr J - mg Sin给 式两边同时乘以LdV-gsind^ 对上式两边关于T 积分得1L 2=gcos*c2利用初始条件V - J 0时V - 0故c = -g COS 71由 可解得 日=-* JC o S - c o So上式可化为-\:丰∙Jcos 日-CoS 日0 日=Zdt・s - 4a —周期性变化的函数,周期T = 2π该质点在平衡位置附近作振动时,振动周期与振幅无关,为进一步化简可得sin 2? —sin 22°由于上面算的过程只占整个周期的1/4故由 Sin /sin - = Sin2 2两边分别对二「微分可得COSEdV - Sin -cos ::d ::2 2COSAJIYin 学sin^Sin -cos tP故dr -2 ------- 2 d ‘ I I-Si n 2 电 Si n2 CP \ 2 由于Or VvO 故对应的0 <2—CoSe ∕J 1 —s in 2电 S in 2 申2 2d 「Sin cos : 2故T =4l 2-- d其中 K 2=sin 2玉Y g J 1—K 2sin 2 半2通过进一步计算可得T 仔1 [1 (1* (jκ-(1 3 5 (2n」)*「•]Vg 22江42^4><6汇…Tne 二 Sin 2 2 两边同时积分可得701故T =2.2^0 ■Sin Si n —2 21.5M 为地球的质量;可知,地球表面的重力加速度 g , X 为取地心到无限远的广义坐标,【I :二 Ill- 「,②联立①,②可得:岂 仃;,M 为地球的质量;③解:如图,在半径是R 的时候,由万有引力公式, 对表面的一点的万有引力为PMm* 一 ,①R a当半径增加,R2=R+jl ,此时总质量不变,仍为M,此时表面的重力加速度1可求:由④得:对⑥式进行通分、整理后得:AGM ΔR 3+2ΔRR8 =R 7 CR+ΔR)2A2ΔR R 2AR⑧则当半径改变J N 时,表面的重力加速度的变化为:A2ΔRR2AR =S —。


第一章 思考题1.1平均速度与瞬时速度有何不同?1.2 在极坐标系中,r v r =,θθ r v =.为什么2θ r r a r-=而非r ?为什么θθ r r a 20+=而非θθ r r +?你能说出r a 中的2θ r -和θa 中另一个θ r 出现的原因和它们的物理意义吗?1.3 在内禀方程中,n a 是怎样产生的?为什么在空间曲线中它总沿着主法线方向?当质点沿空间运动时,副法线方向的加速度b a 等于零,而作用力在副法线方向的分量b F 一般不等于零,这是不是违背了牛顿运动定律呢?1.4 在怎样的运动中只有τa 而无n a ?在怎样的运动中又只有n a 而无τa ?在怎样的运动中既有n a 而无τa ?1.5dt r d 与dt dr 有无不同?dt v d与dtdv 有无不同?试就直线运动与曲线运动分别加以讨论. 1.6人以速度v 向篮球网前进,则当其投篮时应用什么角度投出?跟静止时投篮有何不同?1.7雨点以匀速度v 落下,在一有加速度a 的火车中看,它走什么路经?1.8某人以一定的功率划船,逆流而上.当船经过一桥时,船上的渔竿不慎落入河中.两分钟后,此人才发现,立即返棹追赶.追到渔竿之处是在桥的下游600米的地方,问河水的流速是多大?1.9物体运动的速度是否总是和所受的外力的方向一致?为什么?1.10在那些条件下,物体可以作直线运动?如果初速度的方向和力的方向一致,则物体是沿力的方向还是沿初速度的方向运动?试用一具体实例加以说明.1.11质点仅因重力作用而沿光滑静止曲线下滑,达到任一点时的速度只和什么有关?为什么是这样?假如不是光滑的将如何?1.12为什么被约束在一光滑静止的曲线上运动时,约束力不作功?我们利用动能定理或能量积分,能否求出约束力?如不能,应当怎样去求?1.13质点的质量是1千克,它运动时的速度是k j i v 323++=,式中i 、j 、k 是沿x 、y 、z 轴上的单位矢量。

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
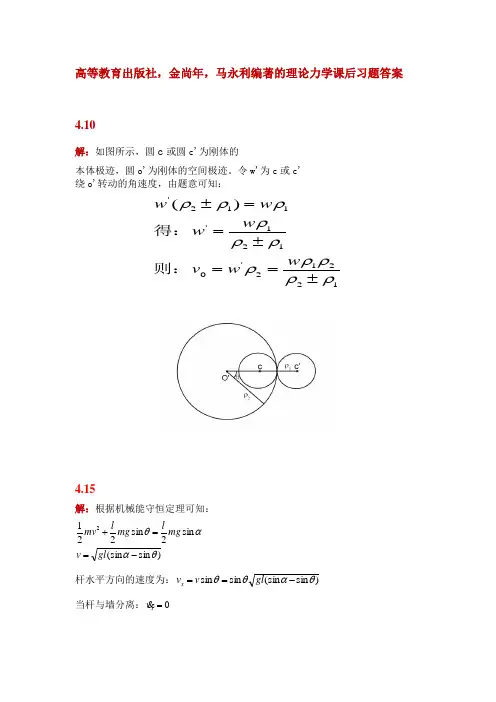
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案 4.10解:如图所示,圆c 或圆c'为刚体的本体极迹,圆o'为刚体的空间极迹。
令w'为c 或c' 绕o'转动的角速度,由题意可知:12212'0121'112')(ρρρρρρρρρρρ±==±==±w w v w w w w 则:得:4.15解:根据机械能守恒定理可知:)sin (sin sin 2sin 2212θααθ-==+gl v mg lmg l mv 杆水平方向的速度为:)sin (sin sin sin θαθθ-==gl v v x当杆与墙分离:0=x v即:0)sin (sin cos )sin (sin cos sin 21=-+--=θαθθαθθgl gl gl v dt d x得:θαsin 23sin = 即:)sin 32arcsin(αθ=4.19如图,该体系中只有一个自由度,取任意位置时棒中点与O 连线与竖直线的夹角θ为广义坐标。
其中设棒的质量为m ,圆周的半径为r ,则棒长为r 3。
另取O 点为重力势能零点。
则对棒θθcos 21212r mg I L o += ,()2221331⎪⎭⎫⎝⎛+=r m r m I o 为棒对O 点的转动惯量。
代入0=∂∂-∂∂θθL L dt d ,得0sin 214522=+θθmgr mr 用θθ=sin 代替,得方程为052=+θθrgrg52=ω,而对于单摆,lg =ω 所以对比得25r l =即等值单摆摆长为25r l =4.20解:如图:设球的半径为R ,设经过时间t 后,会达到如图所示状态,所有参量如图所示。
对其运用牛顿力学方法,有mgRI FR mgma a m F μαμ====''=252mR I =tatv t a v v αω=='=-110同时有对于纯滚动,有 ugtRgt v m m gtv v 25110=='-=ωμμ解上述方程,得代入会得所以有4.23求均匀圆锥体底面圆周上一点的惯量椭球方程。

理论力学(金尚年-XXX编著)课后习题答案详解高等教育出版社的《理论力学课后题答案》一书中,第一章包含了以下三个问题的解答:1.2 题目要求写出在铅直平面内的光滑摆线,并分方程。
解答中使用了微积分和力学原理,得出了运动微分方程。
最后证明了质点在平衡位置附近作振动时,振动周期与振幅无关。
1.3 题目要求证明单摆运动的振动周期与摆长无关。
解答中使用了微积分和力学原理,得出了运动微分方程。
最后通过进一步计算,得出了单摆运动的振动周期公式。
1.5 题目要求使用拉格朗日方程计算质点的运动。
解答中使用了拉格朗日方程,并通过进一步计算得出了质点的运动轨迹。
如图,在半径为R时,地球表面的重力加速度可以由万有引力公式求得:g=\frac{GM}{R^2}$$其中M为地球的质量。
根据广义相对论,地球表面的重力加速度还可以表示为:g=\frac{GM}{R^2}\left(1-\frac{2GM}{c^2R}\right)$$其中c为光速。
当半径增加到R+ΔR时,总质量仍为M,根据XXX展开,可以得到:frac{1}{(R+\Delta R)^2}=\frac{1}{R^2}-\frac{2\DeltaR}{R^3}+\mathcal{O}(\Delta R^2)$$代入上式可得:g'=\frac{GM}{R^2}\left(1-\frac{2GM}{c^2R}\right)\left(1+\frac{2\Delta R}{R}\right)$$ 化简后得:g'=g-\frac{2g\Delta R}{R}$$因此,当半径改变时,表面的重力加速度的变化为:Delta g=-\frac{2g\Delta R}{R}$$2.在平面极坐标系下,设质点的加速度的切向分量和法向分量都是常数,即$a_t=k_1$,$a_n=k_2$(其中$k_1$和$k_2$为常数)。
根据牛顿第二定律,可以得到质点的运动方程:r\ddot{\theta}+2\dot{r}\dot{\theta}=k_2$$ddot{r}-r\dot{\theta}^2=k_1$$其中$r$为极径,$\theta$为极角。
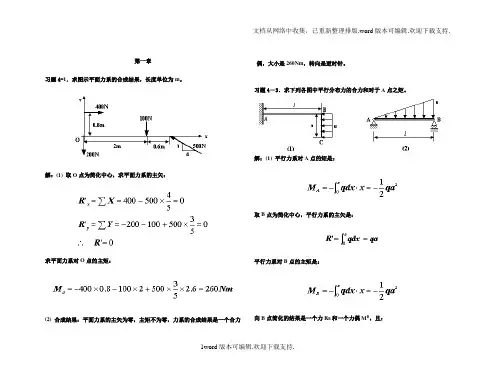
第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:1word版本可编辑.欢迎下载支持.如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
2word版本可编辑.欢迎下载支持.习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:3word版本可编辑.欢迎下载支持.列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:4word版本可编辑.欢迎下载支持.反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案第一章1.2写出约束在铅直平面内的光滑摆线上运动的质点的微分方程,并证明该质点在平衡位置附近作振动时,振动周期与振幅无关.解:设s为质点沿摆线运动时的路程,取=0时,s=0 S== 4 a (1) XY设为质点所在摆线位置处切线方向与x 轴的夹角,取逆时针为正,即切线斜率=受力分析得:则,此即为质点的运动微分方程。
该质点在平衡位置附近作振动时,振动周期与振幅无关,为.1.3证明:设一质量为m 的小球做任一角度0θ的单摆运动运动微分方程为θθθF r r m =+)2( θθsin mg mr = ①给①式两边同时乘以d θ θθθθd g d r sin = 对上式两边关于θ积分得 c g r +=θθcos 212 ② 利用初始条件0θθ=时0=θ 故0cos θg c -= ③ 由②③可解得 0cos cos 2-θθθ-•=lg 上式可化为dt d lg=⨯-•θθθ0cos cos 2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121 由于上面算的过程只占整个周期的1/4故⎰-==0222sin 2sin 124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin 2cos 0=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin022θ=K 通过进一步计算可得glπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K n n K K1.5zp点yx解:如图,在半径是R的时候,由万有引力公式,对表面的一点的万有引力为, ①M为地球的质量;可知,地球表面的重力加速度g , x为取地心到无限远的广义坐标,,②联立①,②可得:,M为地球的质量;③当半径增加,R2=R+,此时总质量不变,仍为M,此时表面的重力加速度可求:④Be ө e tөy由④得:⑤则,半径变化后的g 的变化为⑥对⑥式进行通分、整理后得:⑦对⑦式整理,略去二阶量,同时远小于R ,得⑧则当半径改变 时,表面的重力加速度的变化为:。
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案第一章1.2写出约束在铅直平面内的光滑摆线上运动的质点的微分方程,并证明该质点在平衡位置附近作振动时,振动周期与振幅无关. 解:设s为质点沿摆线运动时的路程,取=0时,s=0S== 4 a (1)设为质点所在摆线位置处切线方向与x 轴的夹角,取逆时针为正,即切线斜率=受力分析得:则,此即为质点的运动微分方程。
该质点在平衡位置附近作振动时,振动周期与振幅无关,为.1.3证明:设一质量为m 的小球做任一角度0θ的单摆运动运动微分方程为θθθF r r m =+)2( θθsin mg mr = ①给①式两边同时乘以d θ θθθθd g d r s i n = 对上式两边关于θ 积分得 c g r +=θθc o s 212 ②利用初始条件0θθ=时0=θ 故0cos θg c -= ③ 由②③可解得 0c o s c o s 2-θθθ-∙=lg 上式可化为dt d lg=⨯-∙θθθ0cos cos 2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121 由于上面算的过程只占整个周期的1/4故⎰-==0222sin 2sin 124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin 2cos 0=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin022θ=K 通过进一步计算可得glπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K n n K K1.5解:如图,在半径是R 的时候,由万有引力公式, 对表面的一点的万有引力为, ①M 为地球的质量;可知,地球表面的重力加速度 g , x 为取地心到无限远的广义坐标,,②联立①, ②可得:,M 为地球的质量;③当半径增加 ,R2=R+ ,此时总质量不变,仍为M,此时表面的重力加速度 可求:④由④得:⑤则,半径变化后的g 的变化为⑥对⑥式进行通分、整理后得:⑦对⑦式整理,略去二阶量,同时远小于R ,得⑧则当半径改变 时,表面的重力加速度的变化为:。
.第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)b(杆ABa(球A ))c(杆AB、CD、整体)d(杆AB、CD、整体)e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体.第一章 静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体.第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N,放在水平梁AC的中央,如图所示。
写出约束在铅直平面内的光滑摆线上运动的质点的微分方程,并证明该质点在平衡位置附近作振动时,振动周期与振幅无关.解:YX设s为质点沿摆线运动时的路程,取=0时,s=0S== 4 a (1)设为质点所在摆线位置处切线方向与x 轴的夹角,取逆时针为正,即切线斜率=受力分析得:则,此即为质点的运动微分方程。
该质点在平衡位置附近作振动时,振动周期与振幅无关,为.证明:设一质量为m 的小球做任一角度0θ的单摆运动运动微分方程为θθθF r r m =+)2( θθsin mg mr = ①给①式两边同时乘以d θ θθθθd g d r sin = 对上式两边关于θ积分得 c g r +=θθcos 212 ② 利用初始条件0θθ=时0=θ 故0cos θg c -= ③ 由②③可解得 0cos cos 2-θθθ-•=lg 上式可化为dt d lg=⨯-•θθθ0cos cos 2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121由于上面算的过程只占整个周期的1/4故⎰-==00222sin 2sin 124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin 2cos 0=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin022θ=K 通过进一步计算可得glπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K n n K Kzp点yx解:如图,在半径是R的时候,由万有引力公式,对表面的一点的万有引力为, ①M为地球的质量;可知,地球表面的重力加速度g , x为取地心到无限远的广义坐标,,②联立①,②可得:,M为地球的质量;③当半径增加,R2=R+,此时总质量不变,仍为M,此时表面的重力加速度可求:④由④得:⑤则,半径变化后的g的变化为⑥Bmge ө e tөy对⑥式进行通分、整理后得:⑦对⑦式整理,略去二阶量,同时远小于R ,得⑧则当半径改变时,表面的重力加速度的变化为:。