2016年苍南县“姜立夫杯”高二数学竞赛

2016年苍南县“姜立夫杯”数学竞赛高二试卷考生注意事项：1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、选择题（本大题共8小题，每小题4分，满分32分，每小题有且仅有一个正确的答案）1．已知集合2{|3100},{|121}A x x x B x m x m =--≤=+≤≤-．当A B =∅时，实数m 的取值范围是（ ）． A ．24m << B ．2m <或4m > C ．142m -<< D ．12m <-或4m > 2．函数()f x 对于任意实数x 满足：()()13f x f x +=-，若()02f =，则()2016f =（ ） A ．12-B ．12C ．2D ．2- 3．已知O 为ABC ∆内一点，若对任意k R ∈，有||||OA OB k BC AC --≥，则ABC ∆一定是（ ）A ．直角三角形B ．钝角三角形C ．锐角三角形D ．不能确定 4．等差数列{}n a 的前n 项和为n S ，已知25235S a =，453325S a =，则6543Sa 的值是（ ） A ．125 B ．85 C ．45 D ．35 5．已知1sin cos 63π⎛⎫α+-α= ⎪⎝⎭，则2sin cos 6π⎛⎫αα+= ⎪⎝⎭（ ） A ．518-B. 518C. 79-D. 796．已知三个不同的平面,,αβγ和两条不重合的直线,m n ，有下列4个命题： ①m n m n ααβ=，，则②m m n n ⊥α⊂βα⊥β，，，则 ③α⊥βγ⊥βαγ，，则 ④m m αβ=⊥γα⊥γ，，则其中正确命题的个数是（ ）A ．1B ．2C ．3D ．47．设,x y 满足约束条件311x y x y y +≤⎧⎪-≥-⎨⎪≥⎩，若02ax by ≤+≤恒成立，则22a b +的最大值是（ ）A ．1B ．89 C ．209D ．4 8．已知函数()22030x x f x x a a x ⎧->⎪=⎨-++<⎪⎩，，的图象上恰有三对点关于原点成中心对称，则a的取值范围为（ ） A ．17(,2)8-- B ．17,28⎛⎤-- ⎥⎝⎦ C ．171,6⎡⎫⎪⎢⎣⎭ D ．171,16⎛⎫⎪⎝⎭二、填空题（本大题共6个小题，每小题6分，满分36分.）9．若正实数,a b 满足284log log 5a b +=和284log log 7b a +=，则48log log a b +的值是▲10．已知点P 是直线:40l kx y ++=()0k >上一动点，PA PB 、是圆22:20C x y y +-=的两条切线，A B 、是切点，若四边形PACB 的最小面积是2，则实数k 的值为 ▲ ．11．在三棱锥D ABC -中，2AB BC ==，AB BC ⊥，BC CD ⊥，DA AB ⊥，DA 与平面ABC 所成的角为45，则二面角A DB C --的平面角的余弦值为▲ ．12.已知函数()2sin f x x =ω()0ω>其中常数，若存在12,03x ⎡⎫∈-⎪⎢⎣⎭π，204x ⎛⎤∈ ⎥⎝⎦，π，使得()()12f x f x =，则ω的取值范围为 ▲ ．13．已知()2()2x f x m n x nx =-⋅++，若{}{}()0(())0x f x x f f x ===≠∅，则m n +的取值范围为 ▲ ．14．已知点(11)A -，，(40)B ，，(22)C ，．平面区域D 由所有满足AP AB AC λμ=+ （1a λ<≤，1b μ<≤）的点()P x y ，组成的区域。

苍教研函[2014] 309号
关于公布2014年苍南县“姜立夫杯”
高中数学竞赛结果的通知
各高级中学：
2014年苍南县“姜立夫杯”高中数学竞赛于12月14日在苍南中学举行，全县共有1001名高一、高二学生参加竞赛，竞赛结果已经揭晓，吴姝瑶等258名学生分获不同组别的一、二、三等奖。

现将获奖名单予以公布。

附件：获奖学生和指导师名单
二○一四年十二月十六日
附件：获奖学生和指导师名单
1．一类高中组
1．1高一段：
一等奖（8名）
二等奖（10名）
三等奖（21名）
1．2高二段：
一等奖（7名）
二等奖（11名）
三等奖（23名）
2．二类高中组
2．1高一段：
一等奖（9名）
二等奖（18名）
三等奖（26名）
2．2高二段：
一等奖（8名）
二等奖（15名）
三等奖（30名）
3．三类高中组
3．1高一段：
一等奖（7名）
二等奖（11名）
三等奖（19名）
3．2高二段：
一等奖（6名）
二等奖（10名）
三等奖（19名）。

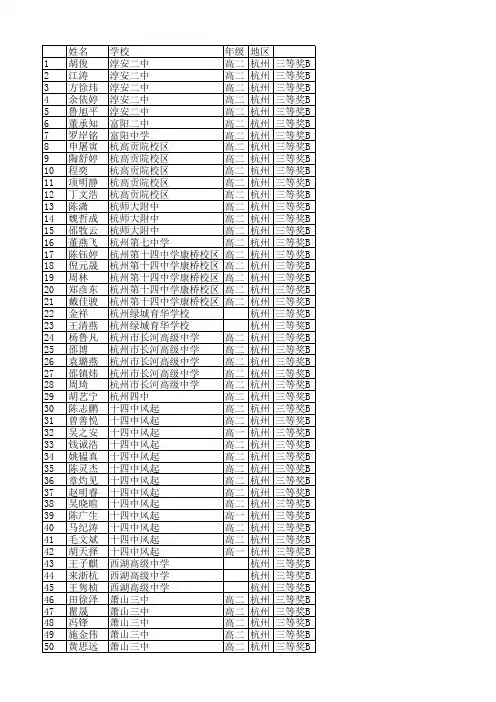
2007年苍南县“姜立夫杯”数学竞赛高一试卷(浙江省)D（A ）－5 （B ）－3 （C ）3（D ）随a,b,c 而变4、若函数f(x)＝a 2sin2x ＋(a －2)cos2x 的图象关于直线x ＝－π对称，则a 的值等于5 （D ）226、已知在数列{a n }满足，a 1＝2＋3，a n ＋2(1－a n )＝1＋a n ，则a 2005的值为 （ ）（A）2＋ 3 （B）2－ 3 （C）3－2 （D）－2－ 3二、填空题（每小题9分，共54分）＋和，则Sf(x)最小值是.12、已知正整数n不超过2005, 并且能表示成不少于60个连续正整数之和，那么，这样的正整数n有个.三、解答题（每小题20分，共60分）13、已知函数y＝sinx＋asin2xcosx..（1）当sinx＝1时，求y的值；（2分）（2）若函数的最大值为1，求实数a的取值范围. （18分）14、n2(n≥4)个正数排成n行n列a11a12a13 (1)a21a22a23 (2)a31a32a33 (3)a24＝nn.15、某公司离火车站40千米，有12名该公司的职员出差，须从公司出发赶到火车站，他们步行的速度为4千米／时，当时公司仅有一辆同时可送4人的轿车，其速度为52千米／时. 要求在3小时内将12名职员送到车站，还希望轿车第一批送的职员能尽早地到车站买票. 试问第一批职员最早能比3小时提前多少时间赶到车站.江苏省苏州实验中学2005年暑期竞赛数学情况调查测试卷（参考答案）1、 B 原函数即为y ＝2＋2(x －1)＋1x 3、C 容易判断f(x)＋f(－x)＝8，且lglog 310＝ lg lg10lg3 ＝ －lg lg3lg10＝ －lglg3，故有f(lglog 310)＋ f(lglg3)＝8，从而f(lglg3)＝3. 选C4、C 函数f(x)＝a 2sin2x ＋(a －2)cos2x 的图象关于直线x ＝ －π8对称，则f(－π8)应取得函数的最大值或最小值。

2012年苍南县“姜立夫杯”数学竞赛高二试卷考生注意事项：1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、 选择题（本大题共8小题，每小题4分，满分32分，每小题有且仅有一个正确的答案）1、已知+∈∈R y R x ,，集合}1,2,{},1,,1{2+--=---++=y yy B x x x x A ，若A=B ，则22y x +的值是（ ）A. 5B. 4C. 25D. 10 2、命题P ：6πα≠， 命题q ：1sin 2α≠，则p 是q 的（ ） A. 充分且必要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分又不必要条件3、如图，四边形ABCD 中，1AB AD CD ===，BD =BD CD ⊥.将四边形ABCD 沿对角线BD 折成四面体A BCD '-，使平面A BD '⊥平面BCD ，则下列结论正确的是（ ）A. A C BD '⊥B. 90BA C'∠=C. CA '与平面A BD '所成的角为30D. 四面体A BCD '-的体积为134、多面体ABCD A BC D -的直观图，正视图，俯视图，侧视图如下所示． ） A ．31112a B ．312a C ．334a D ．356aABCD正视图侧视图5、设()11xf x x +=-，又记()()()()()11,,1,2,,k k f x f x f x f f x k +=== 则()2012f x =（ ） A ．11x x +- B ．11x x -+ C ．x D ．1x-6、设点(1,0)A ，(2,1)B ，如果直线1ax by +=与线段AB 有一个公共点，那么22a b +有（ ）A. 最小值为15 B.最大值为15 D.7、已知函数21,0,()log ,0,x x f x x x +≤⎧=⎨>⎩则函数1)]([+=x f f y 的零点个数是（ ）A. 1B. 2C. 3D. 48、,,a b c 为互不相等的正数，222a c bc +=，则下列关系中可能成立的是（ ）A ．a b c >>B ．b c a >>C ．b a c >>D ．a c b >>二、填空题（本大题共6个小题，每小题6分，满分36分.）９、已知点(2,)P t 在不等式组40,30x y x y --≤⎧⎨+-≤⎩表示的平面区域内，则点(2,)P t 到直线34100x y ++=距离的最大值为____________．10、如图，在边长为1的正方形ABCD 中，E 为BC 的中点，若F 为正方形内（含边界）任意一点，则AE AF ⋅的最大值为 .11、已知长方体的三条面对角线的长分别为5，4，x ，则x 的取值范围为 .12、在平面直角坐标系中，定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”. 则圆221x y +=上一点与直线20x y +-上一点的“折线距离”的最小值是____________________. 13、对任意x ∈R ，函数()f x 满足1(1)2f x +=，设)()]([2n f n f a n -=， 数列}{n a 的前15项的和为3116-，则(15)f = ． 14、设()f x 是定义在Ｒ上的奇函数，且满足(2)()f x f x +=-；又当01x ≤≤时，1()2f x x =，则1()2x f x ⎧⎫=-⎨⎬⎩⎭＝ 。

2016年浙江省高中数学竞赛试卷参考答案一、选择题（每题6分，共48分）1. A .2. .3. .4. D .5. D.6. B.7. B.8. A .二、填空题（每题7分，12题9分，共51分）9. 36−2017201520162.b b +=− ==11. 2.a = = ==12. 245,,.999x y z =−=== 13. 14. [1,2]£® 15. 8.三、解答题（本大题共有3小题，16题15分，17、18每题18分，共51分）16.设函数22()(53)7f x x k ak x =−−++（,R a k ∈）.已知对于任意的[0,2]k ∈，若12,x x 满足1[,],x k k a ∈+2[2,4]x k a k a ∈++，则12()()f x f x ≥， 求正实数a 的最大值. ½â´ð£ºÓÉÓÚ¶þ´Îº¯Êý22()(53)7f x x k ak x =−−++2532k ak x −+=,¡-¡-¡-¡-¡-¡-¡-¡-¡-¡-¡-¡-¡-¡-¡-¡-¡-¡-¡-¡-£¨3·Ö£©¹ÊÌâÉèÌõ¼þµÈ¼ÛÓÚ¶ÔÈÎÒâµÄ[0,2]k ∈ 2535.22k ak k a −+≥+……………………① 6·Ö£© ¼´¶ÔÈÎÒâµÄ[0,2]k ∈ 22351k k a k −+≤+ £¬202235min 1k k k a k ≤≤ −+≤ +9·Ö£©又2236(1)44411k k k k k −+=++−≥−=++，……………（12分）当且仅当1k =−时取等号，故20223min 41k k k k ≤≤ −+=− +.……………………（15分）所以，正实数a17. 已知椭圆C ：22221x y a b +=（0a b >> ），经过点16(3,)5P ，离心率为35. 过椭圆C 的右焦点作斜率为k 的直线l ，交椭圆于,A B 两点，记,PA PB 的斜率为12,k k . （Ⅰ）求椭圆的标准方程；（Ⅱ）若120k k +=，求实数k .22222925691,925a b a b a −+== 2225,16a b == = 2212516x y += == 0k <<∞ l µÄ·½³ÌΪ(3)y k x =− (3),221,2516y k x x y =−+= 2222(1625)1502254000k x k x k +−+−== 1122(,),(,)A x y B x y £¬Ôò22121222150225400,.16251625k k x x x x k k −+==++= 121212161655,,33y y k k x x −−==−− 122112121616()(3)()(3)55(3)(3)y x y x k k x x −−+−−+=−−= 1122(3),(3)y k x y k x =−=− =12212153625600,5(1625)(3)(3)kk k k x x −+==+−− 35k = =0k = 1228,,55k k ==− 12605k k +=−≠ =k ²»´æÔÚʱ£¬´ËʱбÂÊ12,k k ¾ù²»´æÔÚ£¬²»ºÏÌâÒâ. ËùÒÔ£¬35k = =18. 给定数列{}n x ，证明: 存在唯一分解nn n x y z =−，其中数列{}n y 非负，{}n z 单调不减，并且1()0n n n y z z −−=，00z =.证明：我们只需证明对任意的正整数n ， 满足110()0000n n n n n n n n n x y z y z z y z z z −−=− −= ≥ −≥=, ………(*)………………（6分） 的(),n n y z 存在且唯一。

2018年苍南县“姜立夫杯”数学竞赛高二试题参考答案二、填空题9、(1,1)- 10、2004 11 12 13、0x =14、10a -<< 三、解答题15、解：设l 方程为1(1)y m x -=--，则1(1,0)P m +，(0,1)Q m +-----------------1分 从而可得直线PR 和QS 的方程分别为120m x y m+--=和22(1)0x y m -++=--------2分 又||PRQS，11|221|32||m m RS +++++∴== 又22|||PR QS +==-----------------------------------------------------------------------5分 所以四边形PRSQ 的面积为：2123212PRSQ m S +++==21191()5480m m ++--------------------------------8分 219118(2)54805≥+-=。

所以四边形PRSQ 面积的最小值为185--------------------------------------------------------------10分16、解：设椭圆的离心率为e ，则1||MF e d=，即1||MF de =，--------------------------1分 又12||||2MF MF a +=，所以2||2MF a de =-，---------------------------------------3分由题意可得212||||MF d MF =，所以22(2)d e d a de =-，故22a d e e=+，------5分 由d 不小于左顶点到左准线的距离且不大于右顶点到左准线的距离，即2222222112a a a a a e e ca d a e c c a a ae e c⎧≥-⎪⎪+-≤≤+⇒⇒≤<⎨⎪≤+⎪+⎩-----------------------------9分 11e ≤<时，符合条件的点M 存在， 当01e <<时，点M 不存在。

苍南县“姜立夫杯”2018年高二上学期数学竞赛试卷满分100分,时间120分钟.一、选择题（本大题共8小题，每小题4分，满分32分，每小题有且仅有一个正确的答案） 1.若集合{0}A x x =≥，且A B B ⋂=，则集合B 可能是（ ） A.{}1,2 B.{1}x x ≤ C.{1,0,1}- D.R2.若对任意实数x 都有x x x f x f sin cos 3)(2)(-=-+，则函数()y f x =的图象的对称轴方程为（ ） A ．Z k k x ∈+=,4ππ B ．Z k k x ∈-=,4ππ C ． Z k k x ∈+=,8ππ D ．Z k k x ∈-=,6ππ3.一个水平放置的一个的正三棱锥,其底面是边长为6的正三角形、侧棱长均为5， 其主视图，俯视图如图所示，则其侧视图（ ）A.形状是等腰三角形，面积为133B.形状是等腰三角形，面积为2393 C.不是等腰三角形，面积为 133 D.不是等腰三角形，面积为2393 4.已知在△ABC 中，∠ACB=，AB=2BC ，现将△ABC 绕BC 所在直线旋转到△PBC ，设二面角P ﹣BC ﹣A 大小为θ，PB 与平面ABC 所成角为α，PC 与平面PAB 所成角为β，若0＜θ＜π，则α、sin β的范围分别是（ ）)33,0(],3,0(.πA ]33,0(],3,0(.πB)21,0(],3,0(.πC 1.(0,],(0,)62D π 5.202,()342x f x x x x ≤≤=+-函数的最大值是（ ）A. 5B. 6C.7D.86.已知点()1,1A --．若曲线T 上存在两点,B C ，使ABC ∆为正三角形，则称T 为“正三角形”曲线．给定下列三条曲线：①222x y +=；②()3003x y x +-=≤≤；③1(0)y x x=->．其中，“正三角形”曲线的个数是（ ） A ． 0 B ． 1 C ． 2 D ． 37.如图，圆C 分别与x 轴、y 轴正半轴相切于A 、B ，过劣弧AB 上一点T 作圆C 的切线，分别交x 轴、y 轴正半轴于M 、N 两点，若点Q （2,1）是 切线上一点，则∆MON 周长的最小值为（ ） A ． 8 B ． 10 C ． 12 D ． 548.已知平面向量a ，b ，|a |=1,|b |=2， e 为平面单位向量且|a ·e |+|b ·e |的最大值为7，则下列结论成立的是（ ）A ．|a +b |=|a -b | B.b ·(a -b )=0 C. a ·(a -b )=0 D. min ,||3t R b ta ∈-= 二、填空题（本大题共6个小题，每小题6分，满分36分.） 9. 在ABC △中，2a =，3b =，4c =，则sin 2sin AC= ▲ ． 10. 设{}n a 的公比为q 的等比数列,其前n 项和为n S ,且32420192018,S S S =+ 则q = ▲11. 432(1)0[0,)x x x a x a x -+-++≥∈+∞对恒成立，则a= ▲12.2()3,|(())0}|()0},xf x x ax b x f f x x f x a b φ=++⋅===≠+函数若{{则取值范围是 ▲13.在三棱锥ABC P -中，BC AB ⊥,32,2,AB BC PA PB ===当三棱锥ABC P -体积取最大时，锐二面角P-AC-B 的大小=θθtan ,则 ▲ ．14. 22224560,24x y x y xy x y x y x y +--++=+-+、是实数，则的取值范围是 ▲三、解答题（本大题共3小题，第15、16题各10分,第17题12分,满分32分.要求写出必要的解答过程）15．已知圆22-(2)40)2x a y a a y kx +-=>=+C:（）（与直线交于M 、N 两点， 其中C 为圆心，=2a (1)若, 125CM CN ⋅=-, 求k 的值; =1,k (2)若当CMN ∆面积取最大时，求a 的值.16. 已知函数()2f x x ax b =++.(1) 0a ≠且1b =,求()y f x =在区间0,a ⎡⎤⎣⎦上的最大值； (2) 若,a b Z ∈，且()a b f x +是的零点，求所有可能b 的值.17. 已知{a n }满足，++∈+==N n a a a a n n n ,144,812211 （1)证明：;811≤<+n n a a （2）证明：1211121119n n a a a +++>-+++参考答案一、 选择题（本大题共8小题，每小题4分，满分32分.每小题有且仅有一个正确的答案）二、填空题（本大题共6个小题，每小题6分，满分36分. 请将正确的答案填在横线上）9.8710. 12018 11.214. ]3,313[-- 三、解答题（本大题共3小题，第15、16题各10分,第17题12分,满分32分.要求写出必要的解答过程）15．已知圆22-(2)40)2x a y a a ykx +-=>=+C:（）（与直线交于M 、N 两点 其中C 为圆心，=2a (1)若,125CM CN ⋅=-, 求k的值; =1,k (2)若当CMN ∆面积取最大时，求a 的值.解析：(1) 125CM CN ⋅=-得3cos ,5MCN ∠=- ……2分……2分 1=22k =或 ……1分（其他方法酌情给分）(2)设圆心到直线的距离为d ,S ==……2分当CMN ∆面积取最大时d ……2=4a = ……1分（其他方法酌情给分）16. 已知函数()2f x x ax b =++.(1) 0a ≠且1b =,求()y f x =在区间0,a ⎡⎤⎣⎦上的最大值； (2) 若,a b Z ∈，且()a b f x +是的零点，求所有可能b 的值.解析：（1）当a>0时，()222max 1[1,21],|()|21f x x ax a f x a =++∈+=+ ……2分当a<0时, ()222max 4-4-1[,1],|()|max ||,144a a f x x ax f x ⎧⎫=++∈=⎨⎬⎩⎭……2分=2441,0a a -≤-<⎧⎪⎨⎪⎩，a ……1分（2）()()()20f a b a b a a b b +=++++=得22230a ab b b +++= ……1分2=b -8b ∆必为完全平方数 ……1分2222=b -8b=,()16m N m ∆∈-=令m 得(b-4){{{{42444-44-848444-44-2b m b m b m b m b m b m b m b m --=--=--=--=-+=-+=-+=-+=或或或所有可能b 的值为9、8、-1、0 ……3分17. 已知{a n }满足，++∈+==N n a a a a n n n ,144,812211 （1)证明：;811≤<+n n a a （2）证明：9211111121->++++++n a a a n 解析：（1）0>n a 易得=-+n n a a 1014)12(141441442223222≤+--=+--=-+n n n n n n n n n a a a a a a a a a ……2分∴≤≤∴+,811n n a a 014)12(22<+--n n n a a a ;811≤<∴+n n a a ……2分 （用nnn n n n a a a a a a 14114421+=+=+同样给分）（2）284414422221+=+≤+=+n nn n n n n n a a a a a a a a ……2分 12211+=+≥+n n n n a a a a ,)11(2111+≥++nn a a 111292)11(11--⋅=⋅+≥+n n n a a ,1)21(911-⋅≤+n n n a a ……3分 =+11n a 1)21(91111-⋅-≥+-n n n a a ……2分 92])21()21(211[911111111221->+++-≥++++++-n n a a a n n …1分。

年苍南县“姜立夫杯”高中数学竞赛高一试卷一、选择题（每题5分，共40分）1、三元实数集A=},,{y x xy x +，B=},||,0{y x ，且A=B ，则20062006xy +=（ ）A 、0B 、1C 、2D 、－12、若某等差数列{a n }中，1662a a a ++是一个确定的常数，则其前n 项和S n 中也为确定的常数的是( ）A 、 15SB 、 14SC 、 8SD 、7S 3、设函数121(1)()lg (1)x x f x x x -⎧-<=⎨≥⎩，若1)(0>x f ，则x 0的取值范围是（ ） A 、（0，10） B 、（－1，+∞） C 、（－∞，－2） D 、（－∞，0）∪（10，+∞）4、等差数列}{n a 的前n 项和为S n ，且3184=S S ，则=168S S （ ） A 、81 B 、31 C 、91 D 、103 5、已知集合{|1284,,,}P u u m n l m n l Z ==++∈，集合{|201612,,,}Q u u p q r p q r Z ==++∈，则P 与Q 的关系为（ ）A 、P =QB 、P ∩Q =φC 、 P ∪Q =RD 、P ∪Q =Z6、数列1，2，2，3，3，3，4，4，4，4……，则这个数列的第个数是（ ）A 、62B 、63C 、64D 、657、已知函数f(x)是R 上的减函数，A （0，－2），B （－3，2）是其图象上的两点，则不等式|f(x+2)|>2的解集是（ ）A 、（－1，2）B 、（－∞，－1）∪（2，+∞）C 、（－∞，－5）∪（－2，+∞）D 、（－∞，－3）∪（0，+∞）8、某火车站在节日期间的某个时刻候车旅客达到高峰，此时旅客还在按一定的流量到达。

如果只打开3个检票口，需要30分钟才能使所有滞留旅客通过检票口。

如果打开6个检票口，只需要10分钟就能让所有滞留旅客通过。

2018年苍南县“姜立夫杯”数学竞赛高 二 试 题命题人：薛祖坚一、选择题（每小题5分，共40分）1、动点P 在抛物线26y x =-上运动,定点(0,1)A ，线段PA 中点的轨迹方程是( )．A 、2(21)12y x +=-B 、2(21)12y x +=C 、2(21)12y x -=-D 、2(21)12y x -=2、实数x 、y 满足不等式组010,1220y y x y x x y ω≥⎧-⎪-≥=⎨+⎪--≥⎩，则有( )A 、113ω-≤≤B 、1123ω-≤≤C 、12ω≥-D 、112ω-≤<3、直线y x m =+与抛物线22x y =交于A 、B 两点，O 为坐标原点，且0OA OB ⋅= ，则m 的值等于( )A 、1B 、－1C 、2D 、－24、在圆22(3)(5)2x y -+-=的切线中，在两坐标轴上截距绝对值相等的直线共有（ ）A 、4条B 、5条C 、6条D 、8条 5、方程(1)(1)1(0)x y x +-=≠表示的曲线关于（ ）对称.A 、y x =B 、2y x =+C 、y x =-D 、(1,1)-6、平面直角坐标系中,横、纵坐标都是整数的点称为整点。

那么满足不等式22(||1)(||1)2x y -+-<的整点(,)x y 的个数为( )个.A 、16B 、17C 、18D 、257、已知()(2005)(2006)f x x x =-+的图象与x 轴、y 轴有3个不同的交点，有一个圆恰好经过这三个点，则此圆与坐标轴的另一个交点的坐标是（ ） A 、(0,1) B 、(0,2) C、 D、 8、设,,x y z 都是正数，则2222xy yzx y z +++的最大值为（ ）A 、1B 、2 C、2 D、59、不论,a b 为何值，直线0ax by a b +-+=过定点______________________. 10、若函数()f x 满足()()(),f a b f a f b +=且(1)1f =,则(2)(3)(2005)(1)(2)(2004)f f f f f f +++的值等于__________________.11、若P 是双曲线2213x y -=的右支上的动点，F 是双曲线的右焦点，已知(3,1)A ，则||||PA PF +的最小值是_____________________________. 12、正项数列{}n a 的前n 项和为n S ，且11()2n n nS a a =+，则该数列的通项公式n a =__________ 13、方程221(1)cos2202x x x x--++--=的解为____________________. 14、如果关于x 的不等式|||||1|x a x x -<++的解集为一切实数，那么实数a 的取值范围是_____________________答题卷一、选择题（每小题5分，共40分）二、填空题（每小题5分，共30分）9、_________________ 10、__________________ 11、____________________12、________________ 13、__________________ 14、____________________15、已知过点(1,1)A 且斜率为(0)m m ->的直线l 与,x y 轴分别交于点,P Q ，过,P Q 作直线20x y +=的垂线，垂足为,R S . 求四边形PRSQ 面积的最小值。

2015年苍南县“姜立夫杯”数学竞赛高一试卷考生注意事项：1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、选择题（本大题共8小题，每小题4分，满分32分，每小题有且仅有一个正确的答案）1．已知a 为给定的实数，那么集合{}22320=-+-=M x x x a 的子集的个数为（ ） A ．1 B ．2 C ．4 D ．不确定 2．函数()212()log 23f x x x =--的单调递增区间是（ ）A ．)1,(--∞B ．)1,(-∞C ．),1(+∞D ．),3(+∞ 3．函数221)(xx x f x--=（ ） A 是偶函数但不是奇函数 B 是奇函数但不是偶函数C 既是偶函数又是奇函数D 既不是偶函数也不是奇函数 4．设3log 2=a ，ln 2=b ，125-=c ，则（ ）A ．c b a <<B ．a c b <<C ．<<c a bD ．<<c b a5．设函数()()2log 2x f x m =+,则满足函数f x 的定义域和值域都是实数集R 的实数m 构成的集合为（ ）A ．{}0m m =B ．{}0m m ≤C ．{}0m m ≥D ．{}1m m = 6．已知函数21,0,()log ,0,x x f x x x +≤⎧=⎨>⎩则函数[]()1=-y f f x 的零点个数是（ ）A. 1B. 2C. 3D. 47．如果不等式21x x a <-+的解集是区间()3,3-的子集，则实数a 的取值范围是（ ）A ．(,7)-∞B ．(],7-∞C ．(,5)-∞D ．(],5-∞ 8．已知(),(),()f x g x h x 为一次函数，若对实数x 满足1,1()()()32,1022,0x f x g x h x x x x x -<-⎧⎪-+=+-≤<⎨⎪-+≥⎩，则()h x 的表达式为（ ）A.1()2h x x =-B.1()2h x x =--C.1()2h x x =-+D.1()2h x x =+ 二、填空题（本大题共6个小题，每小题6分，满分36分.）9．已知点在幂函数()yf x 的图象上，则4f ▲ ．10．设,a b 为不相等的两个实数，若二次函数()2f x x ax b =++满足()()f a f b =，则()2f 的值为 ▲ ．11．已知函数315(1)()(1)xa x x f x ax 是实数集R 上的增函数，则实数a 的取值范围为 ▲ ．12．已知奇函数)(x f 在定义域[]3,3-上是减函数，且()2(2)20-+-<f x x f x ，则实数x 的取值范围是 ▲13.已知()f x 为R 上增函数，且对任意∈x R ，都有()34⎡⎤-=⎣⎦xf f x ，则(2)f 的值等于▲14．已知自然数a b c d e 、、、、满足1100a b c d e ≤<<<<≤，则当b da c e++取最小值时，a b c d e ++++=____▲ ___2015年苍南县“姜立夫杯”数学竞赛高一答题卷一、选择题（本大题共8小题，每小题4分，满分32分.每小题有且仅有一个正确的答案）二、填空题（本大题共6个小题，每小题6分，满分36分. 请将正确的答案填在横线上）9.________________________ 10._____________________________ 11._______________________ 12._____________________________ 13._______________________ 14._____________________________三、解答题（本大题共3小题，第15、16题各10分,第17题12分,满分32分.要求写出必要的解答过程）15．设集合}023|{2≤++=x x x A ，}0|{2≤++=b ax x x B ， (1) 若R B A C x x B A C R R =≤<-= )(},21|{)(，求b a ,的值； (2) 若1=b ，且A B A = ，求实数a 的取值范围．16．已知函数()(1)(01)xxf x a k a a a -=-->≠且是定义域为R 上的奇函数.（1）求k 的值；（2）若23)1(=f ，且)(2)(22x f m a a x g x x ⋅-+=-在),1[∞+上的最小值为2-， 求m 的值．17．设二次函数c bx ax x f ++=2)(（0,,,≠∈a R c b a ）满足条件： ①当R x ∈时，(1)(3)-=-f x f x ；②不等式241()21--≤≤+x f x x 对一切实数x 都成立。

2017年苍南县“姜立夫杯”数学竞赛高一试卷考生注意事项：1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、选择题（本大题共8小题，每小题4分，满分32分，每小题有且仅有一个正确的答案）1.已知集合{}R x x x x A ∈=+=,02，则满足{}1,1,0-=B A 的集合B 的个数是（ ） A ．2 B ．3 C ．4 D ．82.若对任意()1,x ∈+∞，不等式0)1)(1(≥+-ax x 恒成立，则a 的取值范围为（ ） A ．0a ≥ B ．0a > C. 1a ≥- D. 1a >-3.函数()f x 的定义域为(,1)(1,)-∞+∞，且(1)f x +为奇函数，当1x >时，2()21216f x x x =-+，则方程()f x m =有两个零点的实数m 的取值范围是（ ） A ．()6,6- B ．()6,2- C ．()()+∞⋃-∞-,66, D ． ()()6,22,6⋃--4.关于函数31)212()(x x f x x-=和实数m 、n 的下列结论中正确的是（ ）A ．若n m <<-3，则)()(n f m f <B ．若0<<n m ，则)()(n f m f <C ．若)()(n f m f <，则22n m < D ．若)()(n f m f <，则33n m < 5.形如)0,0(||>>-=b c cx by 的函数因其图象类似于汉字中的“囧”字，故称为“囧函数”．若函数12)(++=x xa x f )1,0(≠>a a 有最小值，则当1,1==bc 时的“囧函数”与函数||log x y a =的图像交点个数为（ ）个． A ．6 B ．4 C ．2D ．16.已知函数*()21,f x x x =+∈N ，若存在正整数0x ，n ，使000()(1)()63f x f x f x n +++++=成立，则称0(,)x n 为函数()f x 的一个“生成点”，函数()f x 的“生成点”共有（ ）个． A ．0 B ．1 C ．2 D ．37.定义在),0(+∞上的函数)(x f 满足：)(2)2(x f x f =，且当(1,2]x ∈时，x x f -=2)(，若21,x x 是方程=)(x f )10(≤<a a 的两个实数根，则21x x -不可能．．．是（ ） A ．24 B ．72 C ．96 D ．1208.设函数33,0()log 0x x f x x x ⎧≤=⎨>⎩，，若对任意给定的)1(∞+∈，t ，都存在唯一的∈x R ，满足at t a x f f +=222))((，则正实数a 的取值范围是（ ）A ．1[+)2∞， B ．1(+)2∞， C ．[2+)∞，D ．(2+)∞， 二、填空题（本大题共6个小题，每小题6分，满分36分.）9.已知函数()()222,1log 1,1x x f x x x ⎧-≤⎪=⎨-+>⎪⎩ ，且()3-=a f ，则()6f a -=___▲___．10.已知函数⎪⎪⎩⎪⎪⎨⎧>-+≤=0,220,)21()(x x x x x f x，则满足方程1))((=t f f 不同的t 的值有___▲___个.11.若方程)1ln(2ln +=x kx没有实数根，那么实数k 的取值范围是___▲___． 12.若函数)0(2)(2>+=x x x x f ，)()(1x f x f =，))(()(1x f f x f n n =+，*∈N n ,则2017()f x 在[1,2]上的值域为___▲___．13.定义函数I x x f y ∈=),(，若存在常数M ，对于任意I x ∈1，存在唯一的I x ∈2，使 得M x f x f =+2)()(21，则称函数)(x f 在I 上的“均值”为M ，已知2()log f x x =，2017[1,2]x ∈，则函数x x f 2log )(=在2017[1,2]上的“均值”为___▲___．14.已知函数()(()121log 21x a xm m f x x ++-=+-+，（0a >且1a ≠），且[],0x k k k ∈->的最大值与最小值之和为4，则m =___▲___．2017年苍南县“姜立夫杯”数学竞赛高一答题卷一、选择题（本大题共8小题，每小题4分，满分32分.每小题有且仅有一个正确的答案）二、填空题（本大题共6个小题，每小题6分，满分36分. 请将正确的答案填在横线上）9. ______________________________ 10._____________________________ 11. _____________________________ 12._____________________________ 13. _____________________________ 14._____________________________三、解答题（本大题共3小题，第15、16题各10分,第17题12分,满分32分.要求写出必要的解答过程）15．已知集合A 是函数][))(2(log )(a x a x x g a ---=)1,0(≠>a a 且的定义域，集合B 和集合C 分别是函数x x f 39)(-=的定义域和值域．(1)求集合A ，B ，C ；(2)若C C A = ，求实数a 的取值范围．16．已知2()(,,0)f x ax bx c a b R a =++∈≠．(1)当1a =，2b =时，若02)(=-x f 有且只有两个不同的实根，求实数c 的取值范围； (2)若0>a ，函数)(x f 在区间[]5,2--上不单调，且它的图像与x 轴相切，求ab f 2)2(-的取值范围．17.已知函数2()()21xxf x x R =∈+． (1)求函数()f x 的值域；(2)是否存在正整数m ，n 使114(1)2()14(1)2n n m f m m+--<--成立？若存在，求出所有符合条件的有 序数对(m ，n )；若不存在，请说明理由．2017年苍南县“姜立夫杯”数学竞赛高一参考答案一、选择题（本大题共8小题，每小题4分，满分32分）二、填空题（本大题共6个小题，每小题6分，满分36分）9. 32-10. 6 11. 04k << 12. 2017201722[21,31]-- 13.2017214. -2 三、解答题（本大题共3小题，满分32分.要求写出必要的解答过程）15．已知集合A 是函数][))(2(log )(a x a x x g a ---=)1,0(≠>a a 且的定义域，集合B 和集合C 分别是函数x x f 39)(-=的定义域和值域．(1)求集合C B A ,,；(2)若C C A = ，求实数a 的取值范围．【解析】(1)由0))(2(>---a x a x 得0))(2(<--a x a x ， 又因为1,0≠>a a 且，所以a x a 2<<，所以A {|2}x a x a =<<． 对于函数x x f 39)(-=，由039≥-x 得2≤x ，{|2}B x x =≤，所以9390<-≤x ，所以[)3,039)(∈-=x x f ，=C {|03}x x =≤<． …………6分(2)若C C A = ，则C A ⊆，则有⎪⎩⎪⎨⎧≤≠>3210a a a ⇒230≤<a 且1≠a ，所以实数a 的取值范围是230≤<a 且1≠a ． …………10分16．已知2()(,,0)f x ax bx c a b R a =++∈≠．(1)当1a =，2b =时，若02)(=-x f 有且只有两个不同的实根，求实数c 的取值范围； (2)若0>a ，函数)(x f 在区间[]5,2--上不单调，且它的图像与x 轴相切，求ab f 2)2(-的取值范围．【解析】1)1(2)()1(22-++=++=c x c x x x f 212<-<-∴c31<<-∴c …………4分4,0)()2(2=-=∆=∴ac b x f x x f 则）（轴相切，的图像与函数aca b 4)(2=∴ []上不单调，，在区间25)(--x f ()()5,2,4,102b bx a a ∴=-∈--∴∈对称轴又24242242242)2(22-++=-++=-++=-a b a b a b a b a c a b a b c b a a b f(),10,4,∈=t t ab设22(2)816(2)12(2)3629324(2)4(2)42f t t t t t b a t t t ++-+-+-===++---- ()4,10t ∈(2)68)2f b a ∴-的取值范围为[，…………10分17.已知函数2()()21xxf x x R =∈+． (1)求函数()f x 的值域；(2)是否存在正整数m ，n 使114(1)2()14(1)2n n m f m m+--<--成立？若存在，求出所有符合条件的有 序数对(m ，n )；若不存在，请说明理由．17．解：(1) 21()12121x x x f x ==-++ 因为20x>，所以211x+>，所以10121x<<+， 所以11021x -<-<+， 所以101121x <-<+， 所以()(0,1)f x ∈. …………4分(2)由114(1)2()14(1)2n n m f m m+--<-- 可得，即，即，因为，所以，所以m<4， 且因为， 所以m=1或2或3，当m=1时，由（*）得，，所以n=1； 当m=2时，由（*）得，，所以n=1或2； 当m=3时，由（*）得，，所以n=2或3或4，综上，存在符合条件的所有有序实数对为：． ……12分。

2010年苍南县“姜立夫杯”数学竞赛高二试卷考生注意事项：本卷共有17道题目，全卷满分100分，考试时间120分钟.答题前，务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 本卷所有试题都必须用蓝色或黑色笔在答题卷上书写，在试题卷上作答无效. 本卷解答一律不准使用计算器.一、选择题（本大题共8小题，每小题4分，满分32分，每小题有且仅有一个正确的答案） 1．已知：b a ,为实数，则“a ＞b ”是“a 1＜b1”的 （ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分又不必要条件2．)(x f 是定义在R 上的奇函数，对任意R x ∈总有)()27(x f x f -=+，则)27(-f 的值为（ ）A ．0B ．7C ．27 D ．-27 3．022120cos 41cos 79cos 241cos 79cos ⋅⋅⋅-+的值为 （ ） A ．41 B ．31 C ．21 D ．434．经过点P （-1，1）引直线l 交两坐标轴于A 、B ，且∆AOB 的面积为3（O 为原点），若这样的直线l 共有n 条，则n= （ ）A ．1B ．2C ．3D ．45．某几何体的一条棱长为7，在该几何体的正视图中，这条棱的投影是长为6的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为 a 和b 的线段，则b a +的最大值为（ ）A ．52B ．4C ．32D ．22 6．函数x x y 3247-+-=的值域为 （ ）A ．[1，2]B ．[0，2]C ．[1，3]D ． (]3,07．把一根长度为6的铁丝截成任意长度的3段，则能构成三角形的概率为 （ ） A ．41 B ．21 C ．43 D ．54∆ABC的外接圆圆心D ，且DA+DC=λDB （R ∈λ），则满足条件的函数)(x f 有（ ）A ．6个B ．10个C ．12个D ．14个二、填空题（本大题共6个小题，每小题6分，满分36分，请将正确的答案填在横线上）9．已知：∆ABC 三个顶点的坐标为A （-2，1），B （6，1），C （-2，16），则∆ABC 的内切圆方程为 . 10．已知：69222++m是一个平方数，则正整数m = .11、设45)c o s1)(sin 1(=++θθ，k nm-=--)cos 1)(sin 1(θθ，其中n m k ,,都是正整数，n m ,互质，则n m k ++= .12．在直角坐标系中，如果两点A （b a ,），B （b a --,）在函数)(x f y =的图象上，那么[A ，B]为函数)(x f 的一组关于原点的中心对称点，（[A ，B]与[B ，A]看作一组），函数⎪⎩⎪⎨⎧+=),1(log ,2cos )(2010x x x g π关于原点的中心对称点的组数为 .13．如果集合A 、B 、C （其中可以有相同）的并集C B A U U ={1，2，3，4}，那么有序的三元集合组（A ，B ，C ）的个数为 . 14．设正项数列{n a }满足11112121=++⋅++++n n n n n n a a a a a a （*N n ∈），631=+a a ，321,,a a a 单调递增且成等比数列，n S 为{n a }的前n 项和，记[x ]为不超过x 的最大整数，则[2008S ]= .2010年苍南县“姜立夫杯”数学竞赛高二答题卷二、填空题（本大题共6个小题，每小题6分，满分36分，请将正确的答案填在横线上） 9． 10． 11． 12． 13． 14．三、解答题（本大题共3小题，第15题、16题各10分，17题12分，满分32分，要求写出必要的解答过程） 15．已知：3)3(cos 32)3cos()3sin(2)(2--+--=πππx x x x f（1）求)(x f 的最大值及取得最大值时相应的x 的值.x ≤0 x ＞0（2）若函数a x f y -=)2(在区间[0，4π]上恰有两个零点1x ，2x ，求)tan(21x x +的值.16．在数列{n a }中，已知1a =2，n n n a a a 2)1(1=++ （1）求数列{n a }的通项公式.（2）记*))(1(N n a a b n n n ∈-⋅=，数列{n b }的前n 项和为n T ，求证n T ＜3.17．已知：集合A={811610|),(22+--+y x y x y x ＜0}，B={y y x |),(≥8||+-t x } （1）若A ∩B ≠φ，求实数t 的取值范围.（2）设点P （8,t ）∈A ，集合A 、B 所表示的两个平面区域的边界相交于点M ，N ，求PNPM 11+的最小值.2010年苍南县“姜立夫杯”数学竞赛高二卷答案一、选择题：DADD BAAC 二、填空题：9．9)4()1(22=-+-y x 10．10 11．27 12．1004 13．2401 14．5352 三、解答题：15解：（1）)32sin(2)(π-=x x f当2232πππ+=-k x ， 125ππ+=k x )(Z k ∈时 )(x f 的最大值为2…………………………………………………………5分（2）a x a x f y --=-=)34sin(2)2(π结合图像可知：πππ=-+-343421x xπ12521=+x x 32)tan(21+=+∴x x …………………………10分 16解：（1）由已知可得：n a ＞0 )11(21111-=-+nn a a11)21()11(11-⋅-=-n n a a 122-=∴n n n a …………………………6分（2）22121)12(2)1(2-+=-=-=n n nnn n n a a b ＜221-n ≤1121221--=-n n n （n ≥2） ++=∴21b b S n …n b +＜+++221212…121-+n 1213--=n ＜3…………12分17、解（1）集合A={22)8()5(|),(-+-y x y x ＜8}当射线8+-=t x y （x ≥t ）与圆8)8()5(22=-+-y x 相切时 可得1=t 或9，9=t （舍去）；当射线8+-=x t y （x ≤t ）与圆8)8()5(22=-+-y x 相切时t ∴的范围为1＜t ＜9……………………………………………………6分（2）如图：设集合A 所表示的圆与x 轴平行的直径为CD ，MP 的延长线与圆的另一个交点为N /则PN PM 11+≥PD PC PNPM PN PM ⋅=⋅=⋅222/ ≥2244==+CD PD PC 当5=t 时等号成立 PN PM 11+∴的最小值为22………………12分。

各地市、有关学校：
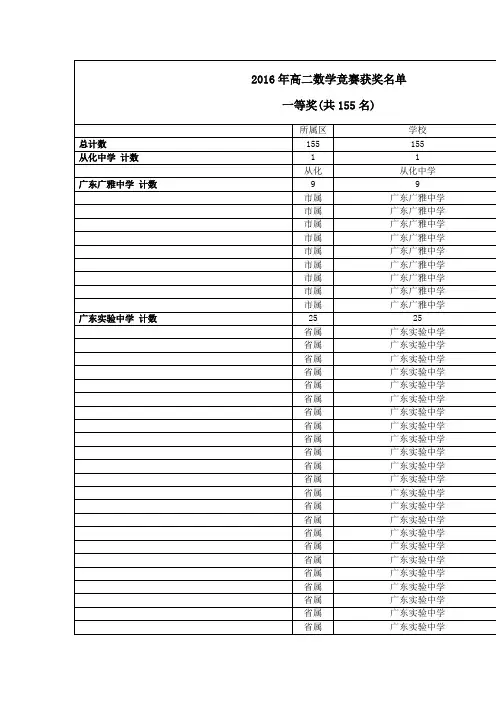
2016年全国高中数学联合竞赛浙江赛区的阅卷工作基本结束.现将成绩优异的学生名单向社会公布，名单见下页。

以下是几点说明：
1. 中国数学会分配给浙江赛区一等奖名额为48名，同时要求按照120%比例上报名单。

2. 公示时间为9月17日至9月22日。

若有异议者，请向各地市教研员反映，由各地市集中向浙江省数学会提出。

恕不接待个人申诉。

3. 一等奖的最终成绩由中国数学会确定。

浙江省数学会
2016.9.15
2016年全国高中数学联赛浙江赛区一等奖候选名单公示。

2016年浙江省高中数学竞赛
通知
各县（市）教育局教研室、有关学校：
2016年浙江省高中数学竞赛由浙江省数学会组织举办，嘉兴市参赛组织工作由嘉兴市中学数学教学分会负责。

现将有关事宜通知如下：
1、竞赛时间：2016年4月17日（星期日）上午9：00---11：00。

2、参赛对象：
（1）高二学生参加A组竞赛。

（适当控制人数）
（2）高三学生参加B组竞赛。

3、试卷形式：分A、B卷，“一卷两制”，即A卷在B卷基础上加2道“附加题”。

B卷共20题，其中选择题10题、填空题7题、解答题3题。

4、考试内容按《浙江省2016年数学高考考试说明》要求。

B卷难度与浙江省高考数学题难度相当，A卷附加题的难度略有提高。

5、参赛报名：学校以学生自愿参加为原则，组织学生报名，收费：每人20元。

统计名单制成电子表格并报县（市）教研室，格式：
学校于2016年3月5日之前将参赛名单报县（市）教研室，县（市）教研室于3月10日之前将参赛人数报中数分会，县（市）参赛名单汇总于阅卷当日上报。

6、组织管理：本项竞赛由浙江省数学会普及工作委员会组织、命题、
评奖（分A、B组）。

在省级评奖基础上由中数分会评定嘉兴市级奖。

嘉兴市各县（市）设考点。

各考点有关考场布置、监考人员的安排均参照全国“高中数学联赛”的有关规定和条例。

嘉兴市中学数学教学分会
2016年1月10日。