2014苍南县姜立夫杯数学竞赛

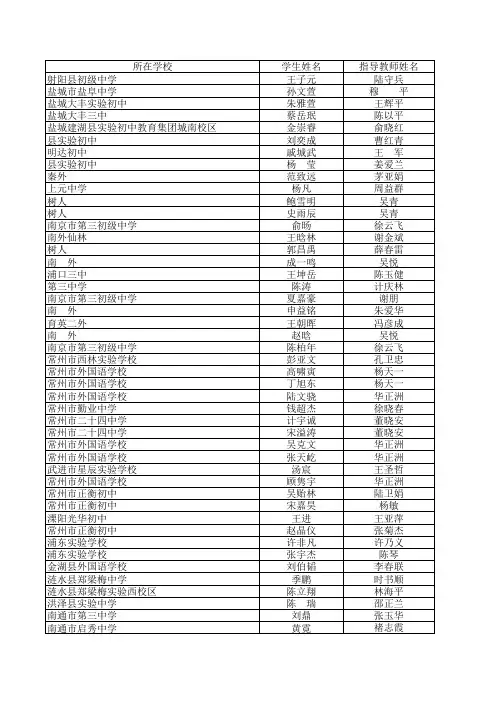
2015年苍南县“姜立夫杯”数学竞赛高一试卷考生注意事项：1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、选择题（本大题共8小题，每小题4分，满分32分，每小题有且仅有一个正确的答案）1．已知a 为给定的实数，那么集合{}22320=-+-=M x x x a 的子集的个数为（ ） A ．1 B ．2 C ．4 D ．不确定 2．函数()212()log 23f x x x =--的单调递增区间是（ ）A ．)1,(--∞B ．)1,(-∞C ．),1(+∞D ．),3(+∞ 3．函数221)(xx x f x --=（ ）A 是偶函数但不是奇函数B 是奇函数但不是偶函数C 既是偶函数又是奇函数D 既不是偶函数也不是奇函数 4．设3log 2=a ，ln 2=b ，125-=c ，则（ ）A ．c b a <<B ．a c b <<C ．<<c a bD ．<<c b a5．设函数()()2log 2xf x m =+,则满足函数()f x 的定义域和值域都是实数集R 的实数m构成的集合为（ ）A ．{}0m m =B ．{}0m m ≤C ．{}0m m ≥D ．{}1m m = 6．已知函数21,0,()log ,0,x x f x x x +≤⎧=⎨>⎩则函数[]()1=-y f f x 的零点个数是（ ）A. 1B. 2C. 3D. 47．如果不等式21x x a <-+的解集是区间()3,3-的子集，则实数a 的取值范围是（ ）A ．(,7)-∞B ．(],7-∞C ．(,5)-∞D ．(],5-∞ 8．已知(),(),()f x g x h x 为一次函数，若对实数x 满足1,1()()()32,1022,0x f x g x h x x x x x -<-⎧⎪-+=+-≤<⎨⎪-+≥⎩，则()h x 的表达式为（ ）A.1()2h x x =-B.1()2h x x =--C.1()2h x x =-+D.1()2h x x =+ 二、填空题（本大题共6个小题，每小题6分，满分36分.）9．已知点(在幂函数()y f x =的图象上，则()4f = ▲ ．10．设,a b 为不相等的两个实数，若二次函数()2f x x ax b =++满足()()f a f b =，则()2f 的值为 ▲ ．11．已知函数()315(1)()(1)x a x x f x ax ì--<ï=í³ïî是实数集R 上的增函数，则实数a 的取值范围为 ▲ ．12．已知奇函数)(x f 在定义域[]3,3-上是减函数，且()2(2)20-+-<f x x f x ，则实数x 的取值范围是 ▲13.已知()f x 为R 上增函数，且对任意∈x R ，都有()34⎡⎤-=⎣⎦xf f x ，则(2)f 的值等于▲14．已知自然数a b c d e 、、、、满足1100a b c d e ≤<<<<≤，则当b da c e++取最小值时，a b c d e ++++=____▲ ___2015年苍南县“姜立夫杯”数学竞赛高一答题卷一、选择题（本大题共8小题，每小题4分，满分32分.每小题有且仅有一个正确的答案）二、填空题（本大题共6个小题，每小题6分，满分36分. 请将正确的答案填在横线上）9.________________________ 10._____________________________ 11._______________________ 12._____________________________ 13._______________________ 14._____________________________三、解答题（本大题共3小题，第15、16题各10分,第17题12分,满分32分.要求写出必要的解答过程）15．设集合}023|{2≤++=x x x A ，}0|{2≤++=b ax x x B ， (1) 若R B A C x x B A C R R =≤<-= )(},21|{)(，求b a ,的值； (2) 若1=b ，且A B A = ，求实数a 的取值范围．16．已知函数()(1)(01)xxf x a k a a a -=-->≠且是定义域为R 上的奇函数.（1）求k 的值； （2）若23)1(=f ，且)(2)(22x f m a a x g x x ⋅-+=-在),1[∞+上的最小值为2-， 求m 的值．17．设二次函数c bx ax x f ++=2)(（0,,,≠∈a R c b a ）满足条件： ①当R x ∈时，(1)(3)-=-f x f x ；②不等式241()21--≤≤+x f x x 对一切实数x 都成立。

2012年苍南县“姜立夫杯”数学竞赛高二试卷考生注意事项：1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、 选择题（本大题共8小题，每小题4分，满分32分，每小题有且仅有一个正确的答案）1、已知+∈∈R y R x ,，集合}1,2,{},1,,1{2+--=---++=y yy B x x x x A ，若A=B ，则22y x +的值是（ ）A. 5B. 4C. 25D. 10 2、命题P ：6πα≠， 命题q ：1sin 2α≠，则p 是q 的（ ） A. 充分且必要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分又不必要条件3、如图，四边形ABCD 中，1AB AD CD ===，BD =BD CD ⊥.将四边形ABCD 沿对角线BD 折成四面体A BCD '-，使平面A BD '⊥平面BCD ，则下列结论正确的是（ ）A. A C BD '⊥B. 90BA C'∠=C. CA '与平面A BD '所成的角为30D. 四面体A BCD '-的体积为134、多面体ABCD A BC D -的直观图，正视图，俯视图，侧视图如下所示． ） A ．31112a B ．312a C ．334a D ．356aABCD正视图侧视图5、设()11xf x x +=-，又记()()()()()11,,1,2,,k k f x f x f x f f x k +=== 则()2012f x =（ ） A ．11x x +- B ．11x x -+ C ．x D ．1x-6、设点(1,0)A ，(2,1)B ，如果直线1ax by +=与线段AB 有一个公共点，那么22a b +有（ ）A. 最小值为15 B.最大值为15 D.7、已知函数21,0,()log ,0,x x f x x x +≤⎧=⎨>⎩则函数1)]([+=x f f y 的零点个数是（ ）A. 1B. 2C. 3D. 48、,,a b c 为互不相等的正数，222a c bc +=，则下列关系中可能成立的是（ ）A ．a b c >>B ．b c a >>C ．b a c >>D ．a c b >>二、填空题（本大题共6个小题，每小题6分，满分36分.）９、已知点(2,)P t 在不等式组40,30x y x y --≤⎧⎨+-≤⎩表示的平面区域内，则点(2,)P t 到直线34100x y ++=距离的最大值为____________．10、如图，在边长为1的正方形ABCD 中，E 为BC 的中点，若F 为正方形内（含边界）任意一点，则AE AF ⋅的最大值为 .11、已知长方体的三条面对角线的长分别为5，4，x ，则x 的取值范围为 .12、在平面直角坐标系中，定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”. 则圆221x y +=上一点与直线20x y +-上一点的“折线距离”的最小值是____________________. 13、对任意x ∈R ，函数()f x 满足1(1)2f x +=，设)()]([2n f n f a n -=， 数列}{n a 的前15项的和为3116-，则(15)f = ． 14、设()f x 是定义在Ｒ上的奇函数，且满足(2)()f x f x +=-；又当01x ≤≤时，1()2f x x =，则1()2x f x ⎧⎫=-⎨⎬⎩⎭＝ 。

一道2014年浙江高中数学竞赛附加题的探源与解答
冯涛
【期刊名称】《中学数学研究》
【年(卷),期】2015(000)007
【摘要】这道解方程组的题目是2014年浙江省高中数学竞赛试题的附加题22题，对竞赛数学有一定经验的研究者都知道这道题目是所谓的“陈题”，主要考查了构造法的应用，从参考解答中管窥命题者的意图是希望解题者透过代数的表象，看到问题的几何结构．事实上，这道题既可以构造几何意义处理，也可以用纯粹的代数方法求解，正所谓：戏法人人会变，各有巧妙不同；追踪溯源，与上述试题结构极其类似的一道竞赛试题来自前苏联第18届全苏数学奥林匹克10年级题，有兴趣
读者可以自行尝试．
【总页数】4页(P46-49)
【作者】冯涛
【作者单位】浙江省北仑中学,315800
【正文语种】中文
【相关文献】
1.一道值得商榷的高中生物奥赛题——对2008年浙江省一道高中生物竞赛试题的分析 [J], 周兴生
2.2014年广东高中数学竞赛第11题的深入探究 [J], 黄建锋;施剑锋
3.一道2009年浙江省数学竞赛附加题另解 [J], 潘俊
4.2014年浙江省高中数学竞赛 [J],
5.2020年浙江省高中数学竞赛解析几何题的探究及推广 [J], 吴江
因版权原因，仅展示原文概要，查看原文内容请购买。

试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛地点：苍南中学竞赛地点：苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛（高一）苍南县“姜立夫杯”高中数学竞赛（高一）准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛地点：苍南中学竞赛地点：苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛（高一）苍南县“姜立夫杯”高中数学竞赛（高一）准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛地点：苍南中学竞赛地点：苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛（高一）苍南县“姜立夫杯”高中数学竞赛（高一）准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛地点：苍南中学竞赛地点：苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛（高一）苍南县“姜立夫杯”高中数学竞赛（高一）准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛地点：苍南中学竞赛地点：苍南中学苍南县教师发展中心制苍南县教师发展中心制试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛地点：苍南中学竞赛地点：苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛（高二）苍南县“姜立夫杯”高中数学竞赛（高二）准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛地点：苍南中学竞赛地点：苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛（高二）苍南县“姜立夫杯”高中数学竞赛（高二）准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛地点：苍南中学竞赛地点：苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛（高二）苍南县“姜立夫杯”高中数学竞赛（高二）准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛地点：苍南中学竞赛地点：苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛（高二）苍南县“姜立夫杯”高中数学竞赛（高二）准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛时间：2020年12月13日（星期日）上午9：00~11：00 竞赛地点：苍南中学竞赛地点：苍南中学苍南县教师发展中心制苍南县教师发展中心制。

2018年苍南县“姜立夫杯”数学竞赛高二试题参考答案二、填空题9、(1,1)- 10、2004 11 12 13、0x =14、10a -<< 三、解答题15、解：设l 方程为1(1)y m x -=--，则1(1,0)P m +，(0,1)Q m +-----------------1分 从而可得直线PR 和QS 的方程分别为120m x y m+--=和22(1)0x y m -++=--------2分 又||PRQS，11|221|32||m m RS +++++∴== 又22|||PR QS +==-----------------------------------------------------------------------5分 所以四边形PRSQ 的面积为：2123212PRSQ m S +++==21191()5480m m ++--------------------------------8分 219118(2)54805≥+-=。

所以四边形PRSQ 面积的最小值为185--------------------------------------------------------------10分16、解：设椭圆的离心率为e ，则1||MF e d=，即1||MF de =，--------------------------1分 又12||||2MF MF a +=，所以2||2MF a de =-，---------------------------------------3分由题意可得212||||MF d MF =，所以22(2)d e d a de =-，故22a d e e=+，------5分 由d 不小于左顶点到左准线的距离且不大于右顶点到左准线的距离，即2222222112a a a a a e e ca d a e c c a a ae e c⎧≥-⎪⎪+-≤≤+⇒⇒≤<⎨⎪≤+⎪+⎩-----------------------------9分 11e ≤<时，符合条件的点M 存在， 当01e <<时，点M 不存在。

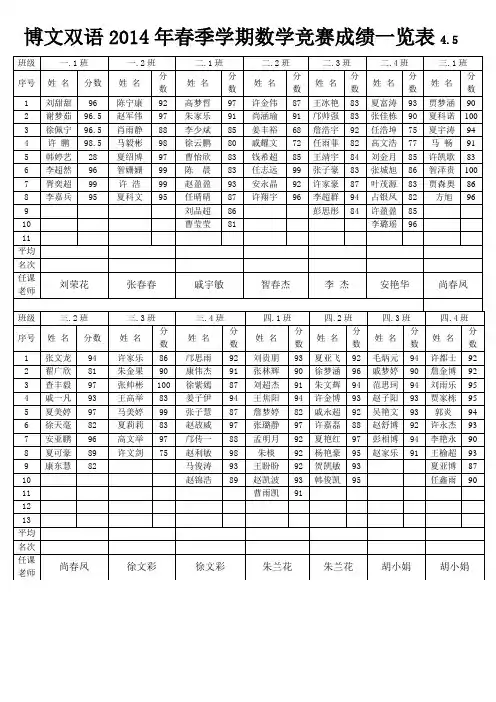
年苍南县“姜立夫杯”高中数学竞赛高一试卷一、选择题（每题5分，共40分）1、三元实数集A=},,{y x xy x +，B=},||,0{y x ，且A=B ，则20062006xy +=（ ）A 、0B 、1C 、2D 、－12、若某等差数列{a n }中，1662a a a ++是一个确定的常数，则其前n 项和S n 中也为确定的常数的是( ）A 、 15SB 、 14SC 、 8SD 、7S 3、设函数121(1)()lg (1)x x f x x x -⎧-<=⎨≥⎩，若1)(0>x f ，则x 0的取值范围是（ ） A 、（0，10） B 、（－1，+∞） C 、（－∞，－2） D 、（－∞，0）∪（10，+∞）4、等差数列}{n a 的前n 项和为S n ，且3184=S S ，则=168S S （ ） A 、81 B 、31 C 、91 D 、103 5、已知集合{|1284,,,}P u u m n l m n l Z ==++∈，集合{|201612,,,}Q u u p q r p q r Z ==++∈，则P 与Q 的关系为（ ）A 、P =QB 、P ∩Q =φC 、 P ∪Q =RD 、P ∪Q =Z6、数列1，2，2，3，3，3，4，4，4，4……，则这个数列的第个数是（ ）A 、62B 、63C 、64D 、657、已知函数f(x)是R 上的减函数，A （0，－2），B （－3，2）是其图象上的两点，则不等式|f(x+2)|>2的解集是（ ）A 、（－1，2）B 、（－∞，－1）∪（2，+∞）C 、（－∞，－5）∪（－2，+∞）D 、（－∞，－3）∪（0，+∞）8、某火车站在节日期间的某个时刻候车旅客达到高峰，此时旅客还在按一定的流量到达。

如果只打开3个检票口，需要30分钟才能使所有滞留旅客通过检票口。

如果打开6个检票口，只需要10分钟就能让所有滞留旅客通过。

2018年苍南县“姜立夫杯”数学竞赛高 二 试 题命题人：薛祖坚一、选择题（每小题5分，共40分）1、动点P 在抛物线26y x =-上运动,定点(0,1)A ，线段PA 中点的轨迹方程是( )．A 、2(21)12y x +=-B 、2(21)12y x +=C 、2(21)12y x -=-D 、2(21)12y x -=2、实数x 、y 满足不等式组010,1220y y x y x x y ω≥⎧-⎪-≥=⎨+⎪--≥⎩，则有( )A 、113ω-≤≤B 、1123ω-≤≤C 、12ω≥-D 、112ω-≤<3、直线y x m =+与抛物线22x y =交于A 、B 两点，O 为坐标原点，且0OA OB ⋅= ，则m 的值等于( )A 、1B 、－1C 、2D 、－24、在圆22(3)(5)2x y -+-=的切线中，在两坐标轴上截距绝对值相等的直线共有（ ）A 、4条B 、5条C 、6条D 、8条 5、方程(1)(1)1(0)x y x +-=≠表示的曲线关于（ ）对称.A 、y x =B 、2y x =+C 、y x =-D 、(1,1)-6、平面直角坐标系中,横、纵坐标都是整数的点称为整点。

那么满足不等式22(||1)(||1)2x y -+-<的整点(,)x y 的个数为( )个.A 、16B 、17C 、18D 、257、已知()(2005)(2006)f x x x =-+的图象与x 轴、y 轴有3个不同的交点，有一个圆恰好经过这三个点，则此圆与坐标轴的另一个交点的坐标是（ ） A 、(0,1) B 、(0,2) C、 D、 8、设,,x y z 都是正数，则2222xy yzx y z +++的最大值为（ ）A 、1B 、2 C、2 D、59、不论,a b 为何值，直线0ax by a b +-+=过定点______________________. 10、若函数()f x 满足()()(),f a b f a f b +=且(1)1f =,则(2)(3)(2005)(1)(2)(2004)f f f f f f +++的值等于__________________.11、若P 是双曲线2213x y -=的右支上的动点，F 是双曲线的右焦点，已知(3,1)A ，则||||PA PF +的最小值是_____________________________. 12、正项数列{}n a 的前n 项和为n S ，且11()2n n nS a a =+，则该数列的通项公式n a =__________ 13、方程221(1)cos2202x x x x--++--=的解为____________________. 14、如果关于x 的不等式|||||1|x a x x -<++的解集为一切实数，那么实数a 的取值范围是_____________________答题卷一、选择题（每小题5分，共40分）二、填空题（每小题5分，共30分）9、_________________ 10、__________________ 11、____________________12、________________ 13、__________________ 14、____________________15、已知过点(1,1)A 且斜率为(0)m m ->的直线l 与,x y 轴分别交于点,P Q ，过,P Q 作直线20x y +=的垂线，垂足为,R S . 求四边形PRSQ 面积的最小值。

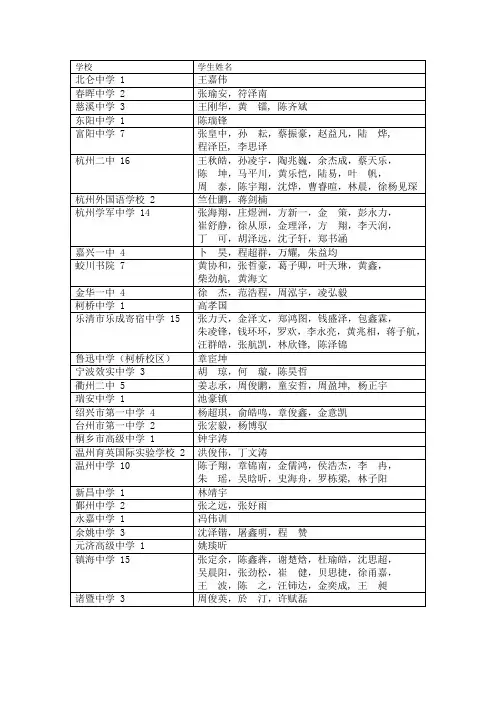
2010年苍南县“姜立夫杯”数学竞赛高二试卷考生注意事项：本卷共有17道题目，全卷满分100分，考试时间120分钟.答题前，务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 本卷所有试题都必须用蓝色或黑色笔在答题卷上书写，在试题卷上作答无效. 本卷解答一律不准使用计算器.一、选择题（本大题共8小题，每小题4分，满分32分，每小题有且仅有一个正确的答案） 1．已知：b a ,为实数，则“a ＞b ”是“a 1＜b1”的 （ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分又不必要条件2．)(x f 是定义在R 上的奇函数，对任意R x ∈总有)()27(x f x f -=+，则)27(-f 的值为（ ）A ．0B ．7C ．27 D ．-27 3．022120cos 41cos 79cos 241cos 79cos ⋅⋅⋅-+的值为 （ ） A ．41 B ．31 C ．21 D ．434．经过点P （-1，1）引直线l 交两坐标轴于A 、B ，且∆AOB 的面积为3（O 为原点），若这样的直线l 共有n 条，则n= （ ）A ．1B ．2C ．3D ．45．某几何体的一条棱长为7，在该几何体的正视图中，这条棱的投影是长为6的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为 a 和b 的线段，则b a +的最大值为（ ）A ．52B ．4C ．32D ．22 6．函数x x y 3247-+-=的值域为 （ ）A ．[1，2]B ．[0，2]C ．[1，3]D ． (]3,07．把一根长度为6的铁丝截成任意长度的3段，则能构成三角形的概率为 （ ） A ．41 B ．21 C ．43 D ．54∆ABC的外接圆圆心D ，且DA+DC=λDB （R ∈λ），则满足条件的函数)(x f 有（ ）A ．6个B ．10个C ．12个D ．14个二、填空题（本大题共6个小题，每小题6分，满分36分，请将正确的答案填在横线上）9．已知：∆ABC 三个顶点的坐标为A （-2，1），B （6，1），C （-2，16），则∆ABC 的内切圆方程为 . 10．已知：69222++m是一个平方数，则正整数m = .11、设45)c o s1)(sin 1(=++θθ，k nm-=--)cos 1)(sin 1(θθ，其中n m k ,,都是正整数，n m ,互质，则n m k ++= .12．在直角坐标系中，如果两点A （b a ,），B （b a --,）在函数)(x f y =的图象上，那么[A ，B]为函数)(x f 的一组关于原点的中心对称点，（[A ，B]与[B ，A]看作一组），函数⎪⎩⎪⎨⎧+=),1(log ,2cos )(2010x x x g π关于原点的中心对称点的组数为 .13．如果集合A 、B 、C （其中可以有相同）的并集C B A U U ={1，2，3，4}，那么有序的三元集合组（A ，B ，C ）的个数为 . 14．设正项数列{n a }满足11112121=++⋅++++n n n n n n a a a a a a （*N n ∈），631=+a a ，321,,a a a 单调递增且成等比数列，n S 为{n a }的前n 项和，记[x ]为不超过x 的最大整数，则[2008S ]= .2010年苍南县“姜立夫杯”数学竞赛高二答题卷二、填空题（本大题共6个小题，每小题6分，满分36分，请将正确的答案填在横线上） 9． 10． 11． 12． 13． 14．三、解答题（本大题共3小题，第15题、16题各10分，17题12分，满分32分，要求写出必要的解答过程） 15．已知：3)3(cos 32)3cos()3sin(2)(2--+--=πππx x x x f（1）求)(x f 的最大值及取得最大值时相应的x 的值.x ≤0 x ＞0（2）若函数a x f y -=)2(在区间[0，4π]上恰有两个零点1x ，2x ，求)tan(21x x +的值.16．在数列{n a }中，已知1a =2，n n n a a a 2)1(1=++ （1）求数列{n a }的通项公式.（2）记*))(1(N n a a b n n n ∈-⋅=，数列{n b }的前n 项和为n T ，求证n T ＜3.17．已知：集合A={811610|),(22+--+y x y x y x ＜0}，B={y y x |),(≥8||+-t x } （1）若A ∩B ≠φ，求实数t 的取值范围.（2）设点P （8,t ）∈A ，集合A 、B 所表示的两个平面区域的边界相交于点M ，N ，求PNPM 11+的最小值.2010年苍南县“姜立夫杯”数学竞赛高二卷答案一、选择题：DADD BAAC 二、填空题：9．9)4()1(22=-+-y x 10．10 11．27 12．1004 13．2401 14．5352 三、解答题：15解：（1）)32sin(2)(π-=x x f当2232πππ+=-k x ， 125ππ+=k x )(Z k ∈时 )(x f 的最大值为2…………………………………………………………5分（2）a x a x f y --=-=)34sin(2)2(π结合图像可知：πππ=-+-343421x xπ12521=+x x 32)tan(21+=+∴x x …………………………10分 16解：（1）由已知可得：n a ＞0 )11(21111-=-+nn a a11)21()11(11-⋅-=-n n a a 122-=∴n n n a …………………………6分（2）22121)12(2)1(2-+=-=-=n n nnn n n a a b ＜221-n ≤1121221--=-n n n （n ≥2） ++=∴21b b S n …n b +＜+++221212…121-+n 1213--=n ＜3…………12分17、解（1）集合A={22)8()5(|),(-+-y x y x ＜8}当射线8+-=t x y （x ≥t ）与圆8)8()5(22=-+-y x 相切时 可得1=t 或9，9=t （舍去）；当射线8+-=x t y （x ≤t ）与圆8)8()5(22=-+-y x 相切时t ∴的范围为1＜t ＜9……………………………………………………6分（2）如图：设集合A 所表示的圆与x 轴平行的直径为CD ，MP 的延长线与圆的另一个交点为N /则PN PM 11+≥PD PC PNPM PN PM ⋅=⋅=⋅222/ ≥2244==+CD PD PC 当5=t 时等号成立 PN PM 11+∴的最小值为22………………12分。

2011年苍南县“姜立夫杯”数学竞赛高一试卷考生注意事项：1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、选择题（本大题共8小题，每小题4分，满分32分，每小题有且仅有一个正确的答案）1．设集合{}{}R T S a x a x T x x S =+<<=>-= ,8|,32|，则a 的取值范围是(A) 13-<<-a (B) 13-≤≤-a(C) 3-≤a 或1-≥a (D) 3-<a 或1->a 2．设偶函数()f x 满足3()8(0)f x x x =-≥，则{|(2)0}x f x ->= (A) {|24}x x x <->或 (B) {|04}x x x <>或 (C) {|06}x x x <>或(D) {|22}x x x <->或3．某学校要召开学生代表大会，规定各班每8人推选一名代表，当各班人数除以8的余数大于5时再增选一名代表。

那么，各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y=[x ]（[x ]表示不大于x 的最大整数）可以表示为 (A) y=⎥⎦⎤⎢⎣⎡+81x (B) y=⎥⎦⎤⎢⎣⎡+82x (C) y=⎥⎦⎤⎢⎣⎡+83x (D) y=⎥⎦⎤⎢⎣⎡+84x 4．若0<abc ，则二次函数()2f x ax bx c =++的图象不．可能．．是5．已知函数|lg |,010,()16,10.2x x f x x x <≤⎧⎪=⎨-+>⎪⎩若,,a b c 互不相等，且()()(),f a f b f c ==则abc 的取值范围是 (A) (1,10)(B) (5,6)(C) (10,12)(D) (20,24)6．以下函数在区间（0，1）内有零点的是（A ）12)(--=x x f x （B ）122)(--=x x f x （C ）123)(--=x x f x （D ）124)(--=x x f x7．设函数00)ln(ln )(<>⎩⎨⎧--=x x x xx f ， 若)()(a f a f ->，则实数a 的取值范围是（A ）（-1，0）∪（0，1） （B ）（-∞，-1）∪（1,+∞） （C ）（-1，0）∪（1,+∞） （D ）（-∞，-1）∪（0,1） 8．已知函数f(x)是定义在实数集R 上的不恒为零的偶函数，且对任意实数x 都有(1)(1)()xf x x f x +=+，则5(())2f f 的值是（ ）（A ） 0 （B ） 12 （C ） 1 （D ） 52二、填空题（本大题共6个小题，每小题6分，满分36分.）9．已知a ，b 为大于1的实数，x x g x x f b a log )(,log )(==，若2)()(21==x g x f 时，21x x >，则a ，b 的大小关系为_____________.10．若m ，n 是方程01lg 22lg 2=+-x x 的两根（m >n ），则nm=_________ 11．已知函数)()(x g x f 和的图象关于原点对称，且12)(2-+=x x x f ，若1)()()(--=x f x g x F λ在区间]1,1[-上是增函数，则λ的取值范围是____________。

苍教研通…2014‟144号各学区、直属小学、市“数学家摇篮工程”苍南县小学基地：第七届苍南县小学生“我爱数学杯”数学知识竞赛成绩已揭晓，这次参赛人数为557人。

获满分奖及一、二、三等奖共217人。

其中满分奖3人，一等奖30人，二等奖69人，三等奖115人，现予以公布。

希望以上获奖同学戒骄戒躁，虚心学习，为全面提高自己的综合素质继续努力。

附件：第七届苍南县小学生“我爱数学杯”数学知识竞赛获奖名单二○一四年五月二十二日满分奖3人学校姓名指导师学校姓名指导师宜山小学陈奕黄开选县实验二小梁敬勋黄孔渊龙港三小潘家晟陈密冬一等奖30人学校姓名指导师学校姓名指导师钱库二小杨咏乐董敏龙港四小项铭铭陈小燕钱库小学蔡宏昕王恒生霞关小学林心怡柯庆云钱库小学金睿涵王恒生龙港五小金政庄再取宜山小学黄万泛黄开选龙港四小温丛函黄振多县实验二小戴世军黄孔渊县实验二小欧文余作为龙港二小尤广贺曹金梳潜龙学校陈子越陈瑞省龙港一小吴圣栋杨雪琎龙港一小黄益明郑爱珍龙港二小赵章毅彭海雁金乡二小林柯顾金燕曹明敏汤文敬县实验二小余联洁余作为龙港五小徐培宇温小芳龙港一小陈钦威姜慧龙港四小杨智赏陈小燕龙港一小陈坦鑫谢树样龙港五小庄铖庄再取龙港四小董桓硕陈小燕县实验二小宋瑞晗黄孔渊龙港一小陈小羽杨雪琎钱库二小王宸董敏龙港四小安孝彦陈小燕县实验三小郑珂谢小娟潜龙学校颜明李中昶龙港八小张星辰朱小暖二等奖69人学校姓名指导师学校姓名指导师金乡小学刘畅黄孝权灵溪二小章一扬杨雅金乡三小陈豪黄增辉龙港一小章圣楠姜慧龙港二小黄锦峰曹金梳潜龙学校上官文倩李中昶县实验一小杨天羽林振兴龙港一小薛芷芊姜慧宜山小学吴登祥朱其令钱库二小陈戈董敏宜山小学陈绍铭朱其令龙港二小林高明刘教训金乡二小杨梦蝶顾金燕曹明敏汤文敬钱库小学金柏宏李来达钱库小学吴昊李来达宜山小学吴狄朱坤畅宜山小学李凡朱其令县实验二小周光荣黄孔渊宜山小学池长江林春玲县实验三小叶德意谢小娟巴曹二小林孝栋林张华龙港四小上官培勋陈小燕龙港四小缪宇航陈小燕县实验一小李潇郑辉霞县实验二小黄声杰陈平龙港四小杜伊诺卢李武龙港五小黄河李静宜山小学陈祥烨黄开选龙港一小陈启轩谢树样龙港六小方舟付广响钱库小学章建国李来达龙港一小朱明泽郑爱珍马站小学金邦景林悦金乡小学黄笑笑汤呈琪巴曹二小林依佳谢尚奔龙港二小褚茂誉彭海雁龙港三小陈皓明陈密冬龙港二小姜增铤彭海雁灵溪二小郑何王园园龙港二小王景玺曹金梳龙港四小陈国栋卢李武灵溪二小澎盛乔蓝瑞力宜山小学杨成昌朱其令龙港四小黄钱生卢李武县实验二小蔡克东黄孔渊县实验二小薛兆波余作为钱库三小陆宏麟洪孝榜县实验二小陈明育余作为灵溪四小吴存康雷顺锐县实验二小朱守领陈平县实验二小周甲鹏黄孔渊龙港四小白如雪卢李武钱库小学项骋李来达龙港四小林颖陈小燕金乡三小刘迪黄增辉灵溪四小林子颂朱晓锦金乡小学林初浩黄孝权龙港六小陈尧付广响龙港五小方子艺李静龙港五小林佳栩温小芳龙港三小陈孝宸陈密冬县实验一小华雨萌郑辉霞龙港一小鲍晶晶郑爱珍金乡二小陈睿顾金燕曹明敏汤文敬县实验二小陈芽芽余作为龙港四小董卓伦陈小燕钱库小学陈政王恒生潜龙学校吴子贺李中昶钱库二小林晗陈仁源三等奖115人学校姓名指导师学校姓名指导师县实验一小陈卓扬吴春阳金乡二小陈立顾金燕曹明敏汤文敬龙港八小林心怡朱小暖龙港五小白福嘉庄再取龙港七小黄昌浦吴传奉县实验一小郑宇恒华婷婷钱库三小陈韦健黄晓吴钱库二小陈柏阳董敏龙港二小李子阳曹金梳潜龙学校蔡世雄陈瑞省龙港四小陈浩楠卢李武钱库小学王政翔洪辉祥龙港二小曹明睿曹金梳龙港一小林浩姜慧钱库三小苏陈俊洪孝榜县实验二小林盈盈余作为金乡二小温学顾金燕曹明敏钱库小学黄昊李来达汤文敬裕靠学校黄雨彤李加环龙港五小高梓萌温小芳县实验二小李培铄黄孔渊龙港四小陈兴市卢李武宜山小学郑德格朱坤畅金乡三小方舒阳温正司潜龙学校周翊轩陈瑞省钱库二小陈一格董敏巴曹二小黄思颖林张华宜山小学林乐婷朱其令龙港八小黄德轩陈乃双县实验二小曾仁泽黄孔渊金乡二小戴心怡顾金燕曹明敏汤文敬县实验二小余德江余作为龙港三小张雨涵吴伟龄灵溪二小陈明鹏郑杰钱库三小黄珊珊黄晓吴县实验三小陈骏林娟宜山小学吴炜炜林春玲灵溪二小陈月幸子曾金星金乡三小雷瑛资黄增辉钱库小学项征李来达钱库小学周瑞敏王恒生巴曹二小邵鑫鑫谢尚奔灵溪二小苏志淮董振宜山小学蔡雨欣朱坤畅龙港八小李雯朱小暖灵溪二小陈披润董振双灵完小姜荣环金仁星龙港八小陈庆乐陈乃双龙港二小郑国剑曹金梳龙港三小陈瑞俊余腊翰钱库小学陈卉李来达灵溪二小林良宇林书语金乡二小黄晨顾金燕曹明敏汤文敬宜山小学金铭朱坤畅宜山小学陈安琦朱坤畅龙港一小徐凡谢树样钱库小学陈希胤王恒生龙港四小潘言陈小燕金乡二小王骁顾金燕曹明敏汤文敬沿浦小学李晓筠金宇共金乡二小陈姿羽顾金燕曹明敏汤文敬龙港三小杨嘉祺陈小丽新安二小李国辉黄瑞听龙港五小李澍怡温小芳龙港五小董国伟李静县实验一小周洁若华婷婷县实验二小董益鸣余作为县实验三小池昊翔王燕燕江山小学徐节叶陈萍县实验二小陈银立余作为钱库二小陈旭侯百宽县实验一小李慧珏郑循进沿浦小学姚志杭陈蒲松新星学校魏玉洁沈素影马站小学蔡大为林悦灵溪二小黄哲蓝瑞力金乡小学陈翔汤呈琪霞关小学刘缘柯庆云潜龙学校杨乐乐李中昶龙港七小杨礼琛吴传奉金乡三小章思琪温正司钱库小学胡伟恒王恒生龙港四小金国豪卢李武江山小学董宗克郑如章巴曹二小黄维杰林张华芦浦小学杨少凯林福橹潜龙学校林元恒李中昶巴曹一小林慧林细守金乡三小刘峰黄增辉马站小学范磊兰加录龙港十小方升健方文泽灵溪四小华伟吴丽环钱库小学林心晨王恒生宜山小学黄文杰陈爱华龙港二小陈锐曹金梳龙港二小林忠献刘教训龙港一小孔舒奕姜慧金乡三小章盈盈温正司县实验二小马晔晔黄孔渊龙港四小李昊陈小燕金乡小学周冬黄孝权潜龙学校黄祖瑶李中昶龙港八小吴登健杨海哨县实验一小吴心怡吴春阳钱库小学陈灿王恒生县实验三小沈德练林娟宜山小学朱其豪林春玲灵溪二小庄乐遥蓝瑞力龙港四小方新宇陈小燕龙港六小陈作杰付广响仙居学校杨思楠杨成朋新星学校花伊静沈素影龙港七小蔡可颖杨碧蓉县实验一小张怡郑辉霞钱库小学张锐李来达。

2014年苍南县“姜立夫杯”数学竞赛高二试卷考生注意事项：1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、 选择题（本大题共8小题，每小题4分，满分32分，每小题有且仅有一个正确的答案）1.函数)2sin(3)(π+=x x f 是（ ）（A ）周期为π2的奇函数 （B ）周期为π2的偶函数 （C ）周期为π的奇函数 （D ）周期为π的偶函数2．若M={(x ，y )| |tan πy |+sin 2πx =0}，N={(x ，y )|x 2+y 2≤2}，则M ∩N 的元素个数是（ ）（A ）4 （B ）5 （C ）8 （D ）93． 如果甲的身高数或体重数至少有一项比乙大，则称甲不亚于乙，在100个小伙子中，如果某人不亚于其他99人，就称他为棒小伙子，那么，100个小伙子中的棒小伙子最多可能有( )（A ）1个 （B ）2个 （C ）50个 （D ）100个 4．有若干个棱长为1的小正方体搭成一个几何体，这个几何体的正视图和侧视图均如右图所示，那么符合这个平面图形的小正方体块数最多时该几何体的体积是 （ ）（A ）6 （B ） 14 （C ）16 （D ） 185．在平面直角坐标系中，方程|x +y |2a +|x －y |2b =1 (a ，b 是不相等的两个正数)所代表的曲线是 ( )（A ）三角形 （B ）正方形（C ）非正方形的菱形 （D ）非正方形的长方形6．已知x ，y 满足⎩⎪⎨⎪⎧y －2≤0，x ＋3≥0，x －y －1≤0，则46--+x y x 的取值范围是 ( )（A ）⎥⎦⎤⎢⎣⎡720,2 （B ）⎥⎦⎤⎢⎣⎡713,1 （C ）⎥⎦⎤⎢⎣⎡73,0 （D ）⎥⎦⎤⎢⎣⎡76,07．设四面体四个面的面积分别为S 1，S 2，S 3，S 4，它们的最大值为S ，记1234=S S S S Sλ+++，则λ一定满足( )（A ）2<λ≤4 （B ）3<λ<4 （C ）2.5<λ≤4.5 （D ）3.5<λ<5.5第4题8. 设函数22,0()log ,0x x f x x x ⎧≤⎪=⎨>⎪⎩，若对任意给定的(2,)y ∈+∞，都存在唯一的x R ∈，满足22(())2f f x a y ay =+，则正实数a 的最小值是（ ）（A ）14 （B ）12（C ）2 （D ）4 二、填空题（本大题共6个小题，每小题6分，满分36分.）9．从正方体的棱和各个面上的对角线中选出k 条，使得其中任意两条线段所在的直线都是异面直线，则k 的最大值是 ．10. 若直线b x y +=被圆122=+y x 所截得的弦长不小于1，则b 的取值范围是 ．11.已知ABC ∆中，AB AC ⊥u u u r u u u r ，||2AB AC -=u u u r u u u r，点M 是线段BC （含端点）上的一点，且()1AM AB AC ⋅+=u u u u r u u u r u u u r ，则||AM u u u u r的取值范围是 ．12．如图，在三棱锥S —ABC 中，若底面ABC 是正三角形，侧棱长SA=SB=SC=3， M 、N 分别为棱SC 、BC 的中点，并且AM ⊥MN ，则三棱锥S —ABC 的外 接球的体积为 .13. 定义在R 上的函数f （x ）满足),(21)3(,1)1()(,0)0(x f xf x f x f f ==-+=且当1021≤<≤x x 时，有)()(21x f x f ≤，则)20141(f 的值为__ __. 14．若三个非零且互不相等的实数a 、b 、c 满足112a b c+=，则称a 、b 、c 是调和的；若满足2a c b +=，则称a 、b 、c 是等差的。