全国中学生物理竞赛课件3：平衡问题探骊【精品】

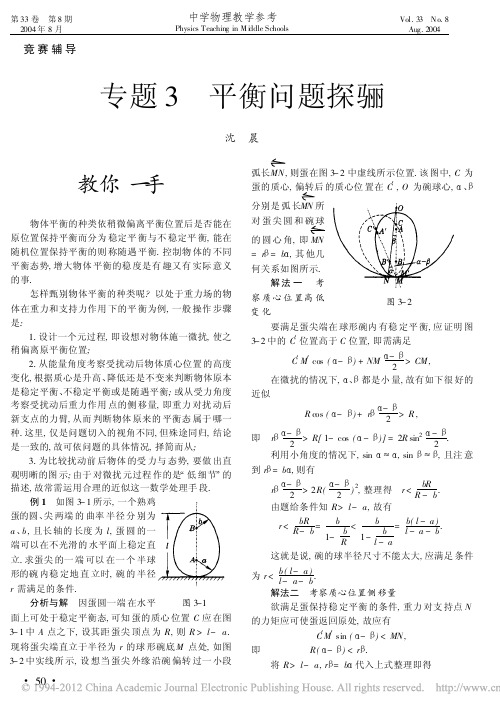
专题3平衡问题探骊教你一手物体平衡的种类依稍微偏离平衡位置后是否能在原位置保持平衡而分为稳定平衡与不稳定平衡，能在随机位置保持平衡的则称随遇平衡．控制物体的不同平衡态势，增大物体平衡的稳度是有趣又有实际意义的事．怎样甄别物体平衡的种类呢?以处于重力场的物体在重力和支持力作用下的平衡为例，一般操作步骤是：１．设计一个元过程，即设想对物体施一微扰，使之稍偏离原平衡位置；２．从能量角度考察受扰动后物体质心位置的高度变化，根据质心是升高、降低还是不变来判断物体原本是稳定平衡、不稳定平衡或是随遇平衡；或从受力角度考察受扰动后重力作用点的侧移量，即重力对扰动后新支点的力臂，从而判断物体原来的平衡态属于哪一种．这里，仅是问题切入的视角不同，但殊途同归，结论是一致的，故可依问题的具体情况，择简而从；３．为比较扰动前后物体的受力与态势，要做出直观明晰的图示；由于对微扰元过程作的是“低细节”的描述，故常需运用合理的近似这一数学处理手段．例1 如图3-１所示，一个熟鸡蛋的圆、尖两端的曲率半径分别为ａ、ｂ，且长轴的长度为ｌ，蛋圆的一端可以在不光滑的水平面上稳定直立．求蛋尖的一端可以在一个半球形的碗内稳定地直立时，碗的半径ｒ需满足的条件．图3-1分析与解 因蛋圆一端在水平面上可处于稳定平衡态，可知蛋的质心位置C应在图3-１中A点之下，设其距蛋尖顶点为R，则Ｒ＞ｌ－ａ．现将蛋尖端直立于半径为ｒ的球形碗底M点处，如图3-２中实线所示，设想当蛋尖外缘沿碗偏转过一小段弧长，则蛋在图3-２中虚线所示位置．该图中，C为蛋的质心，偏转后的质心位置在Ｃ′，Ｏ为碗球心，α、β分别是弧长所对蛋尖圆和碗球的圆心角，即＝ｒβ＝ｂα，其他几何关系如图所示．图3-2解法一 考察质心位置高低变化要满足蛋尖端在球形碗内有稳定平衡，应证明图3-2中的Ｃ′位置高于C位置，即需满足Ｃ′Ｍ′ｃｏｓ（α－β）＋ＮＭ(α－β/２)＞ＣＭ，在微扰的情况下，α、β都是小量，故有如下很好的近似Ｒｃｏｓ（α－β）＋ｒβ(α－β/２)＞Ｒ，即 ｒβ(α－β/２)＞Ｒ［１－ｃｏｓ（α－β）］＝２Ｒｓｉｎ2(α－β/２)．利用小角度的情况下，ｓｉｎα≈α，ｓｉｎβ≈β，且注意到ｒβ＝ｂα，则有ｒβ(α－β/２)＞２Ｒ（(α－β)/２）2，整理得 ｒ＜(ｂＲ/Ｒ－ｂ)．由题给条件知Ｒ＞ｌ－ａ，故有ｒ＜(ｂＲ/Ｒ－ｂ)＝(ｂ/１－(ｂ/Ｒ))＜(ｂ/１－(ｂ/ｌ－ａ))＝ｂ（ｌ－ａ）/(ｌ－ａ－ｂ)．这就是说，碗的球半径尺寸不能太大，应满足条件为ｒ＜ｂ（ｌ－ａ）/(ｌ－ａ－ｂ)． 解法二 考察质心位置侧移量欲满足蛋保持稳定平衡的条件，重力对支持点N的力矩应可使蛋返回原处，故应有Ｃ′Ｍ′ｓｉｎ（α－β）＜ＭＮ，即 R（α－β）＜ｒβ．将Ｒ＞ｌ－ａ，ｒβ＝ｂα代入上式整理即得ｒ＜(ｂ（ｌ－ａ）/ｌ－ａ－ｂ)．例2 如图3-３所示，杆长ｌ＝ａ＋ｂ，质心在Ｃ点，杆的Ａ、Ｂ两端分别支于互相垂直的两个光滑斜面上而处于平衡．试问在图示位置时，此杆的平衡是稳定平衡、随遇平衡还是不稳定平衡?并证明之．图3-3分析与解 杆AB受两斜面支持力及重力这三个不共点的力作用，我们常称之为“三力杆”．非平行力作用下的“三力杆”要处于平衡，三力作用线必汇交，在图3-３中，三力交汇点O与杆AB的质心C连线是竖直的．我们来研究一下杆平衡时的几何位置有什么特点：设右斜面与水平成α角，杆与右斜面成φ0角，在图3-３的△ＢＯＣ中，根据正弦定理有(ｂ/sinα)＝(（ａ＋ｂ）sinφ0/sin（φ0＋９０°－α）)，由此式求得杆平衡时与右斜面夹角满足ｔａｎφ0＝(ｂｃｏｓα/ａsinα)．下面来证明这根“偏心杆”在此位置的平衡是不稳定平衡．证法一 考察质心位置高低．如图3-４所示，当杆与斜面夹角为φ时，质心C的高度以ｙ表示，则ｙ＝（ａ＋ｂ）ｃｏｓφｓｉｎα－ｂｓｉｎ（α－φ）＝ａｓｉｎαｃｏｓα＋ｂｃｏｓαｓｉｎφ＝cos[φ－arctan(ｂcosα/ａsinα)]．即 ｙ＝ｃｏｓ（φ－φ0），显见，当φ＝φ0时，杆质心C的高度有最大值ｙ＝，杆的位置稍有偏离，质心高度就降低，故属于不稳定平衡．图3-4证法二 考察质心对杆的瞬时转动中心的侧移量．如图3-5所示，当杆的两端沿斜面移动时，整根杆的转动中心也在变化．φ＝φ0时，O为杆的瞬时转动中心，重力作用线过O点，力矩为零；当杆转过一小角度，φ＝φ1时，转动中心变成O′，质心位置为C′，比较O′和C′在x轴上投影坐标ｘ与ｘ′之大小，从而确定重力对O′的力矩对杆的作用效果．图3-5由图3-５所示关系得ｘ＝（ａ＋ｂ）ｃｏｓ（φ1＋α）；ｘ′＝αｃｏｓφ1ｃｏｓα－ｂｓｉｎφ1ｓｉｎα，则 ｘ－ｘ′＝ｂｃｏｓφ1ｃｏｓα－ａｓｉｎφ1ｓｉｎα＝ｓｉｎ（φ0－φ1）．因φ1＞φ0，故有ｘ小于ｘ′，即重力将对瞬时转动中心O′构成一负力矩，使杆继续顺时针转动而远离原平衡位置，可见，杆在两光滑斜面间如图3-３所示位置的平衡是不稳定平衡．各种处于稳定平衡状态的物体，其稳定程度不同；处于不稳定平衡状态的物体，也可以通过改变平衡条件使之达到稳定平衡状态，如问题1中的那个熟鸡蛋，以蛋尖端直立于水平面时是不稳定平衡，但置于尺寸合适的球形碗内就可以达到稳定平衡．在生产、生活中有许多实际问题，需要控制物体的平衡条件，提高物体的稳度，我们来例析一二．例3 如图3-６所示，课桌面与水平面夹角成α，在桌面上放一支正六棱柱形铅笔，欲使铅笔既不向下滚动、又不向下滑动．试求：(1)在此情况下铅笔与桌面的静摩擦因数μ．(2)铅笔的轴与斜面母线(斜面与水平面的交线)应成多大的角度φ放置？图3-6分析与解 根据日常我们学习生活的经验，我们在倾斜桌面上放一枝六棱柱形铅笔，当笔杆垂直于斜面母线时，最不易滚下来而会先发生滑动．事实上，当放置在斜面上的铅笔恰能处于平衡时，必有ｍｇｓｉｎα＝ｆ＝μｍｇｃｏｓα，式中f为最大静摩擦力，ｍ为铅笔质量．则μ＝ｔａｎα，即静摩擦因数恰等于斜面倾角的正切值．若μ＞ｔａｎα，放置在斜面上的笔无论以怎样的φ角放置，总不会因发生滑动而破坏平衡．但是，还有一个向下滚动的问题存在．就“稳度”而言，当φ角为某一临界值φ0时，重力作用线超出斜面对铅笔的支持面，则铅笔会在重力矩作用下离开原平衡位置而滚下来．现在来求这个φ0角．如图3-７所示，阴影部分表示笔与桌接触面，正六边形表示笔的横截面，C为铅笔的质心，它在斜面上的投影为O，重力作用线从接触面A“擦边而过”．由图示几何关系可知：ＯＣ＝ａｓｉｎ６０°，ａ为正六边形边长，ＯＢ＝(ａ/２)，∠ＡＣＯ＝α，∠ＢＯＡ＝φ0（注意：ＯＡ垂直于母线，OB垂直于棱线)，在临界状态下(ＯＢ/ｃｏｓφ0)＝ＯＣｔａｎα，故φ0＝ａｒｃｃｏｓ[(１/)ｃｏｔα]．图3－7只要重力作用线落在阴影区内，即有(ａ/２ｃｏｓφ)≥ａｓｉｎ６０°ｔａｎα，ｃｏｓφ≤(１/)ｃｏｔα笔就不会滚动，故放置笔时，应使铅笔的轴与斜面母线所成的角φ＞ａｒｃｃｏｓ[(１/)ｃｏｔα]．例4 如图3-８所示，建造屋顶边缘时，用长度为Ｌ的长方形砖块，一块压着下面一块并伸出砖长的(1/8)，如果不用水泥粘紧，则最多可以堆几层同样的砖刚好不翻倒?这样的几层砖最多可使屋檐“飞”出多长?图3-８分析与解 一块砖的重心就在(Ｌ/２)处，叠放一块砖后，由于伸出(Ｌ/８)，两砖总长(９/８)Ｌ，共同重心在总长的一半处．设有ｎ块相同砖叠放，每块均伸出(Ｌ/８)，则总长为Ｌ＋（ｎ－１）(Ｌ/８)，而总重心在总长度的中间．要使飞檐平衡，ｎ块砖所受总重力作用线不能超出墙壁的支面，即(Ｌ/２)［Ｌ＋（ｎ－１）(Ｌ/８)］≤(7/８)Ｌ，故ｎ≤７．图3-９如图3-９所示，最上面第1块砖要处于平衡而不翻倒，它的重力作用线不能超出其下第2块砖的边线，所以第1块砖能伸出的最大长度为(Ｌ/２)；第1块砖和第2块砖合在一起总长度为(３Ｌ/２)，重心在中间，即距第2块砖边线(Ｌ/４)，第2块砖放在第3块砖上时最多伸出(Ｌ/４)．现在来看三块砖的重心位置：设三块砖重心C3距第3块砖边缘ｘ，由力矩平衡关系知2Ｇｘ＝Ｇ（(Ｌ/２)－ｘ），解得ｘ＝(Ｌ/６)，所以第3块砖只能比下一块砖边线伸出(Ｌ/６)，不难递推，第ｎ块砖伸出量的通式是ｘn＝Ｌ/(２ｎ)，那么七块砖均以最大量伸出，“七级飞檐”最多能飞出的长度为s＝(１＋(１/２)＋(１/３)＋…＋(１/７)）(Ｌ/２)．小试身手１．如图3-１０所示，一矩形导电线圈可绕其中心轴O转动，它处于与轴垂直的匀强磁场中，在磁场的作用下，线框开始转动，最后静止的平面位置是图中的（ ）图3-10２．图3-１１中每一系统的两个球都用一跨过滑轮的线连接起来，问每一种情况各属哪种平衡?图3-11３．如图3-１２所示装置，它是由一个长L的木钉、从木钉上端向左右斜伸出两个下垂的、长为ｌ的细木杆，以及在木杆的末端装有质量同为ｍ的小球而组成．木钉及木杆的质量可忽略，木杆与木钉间夹角为α，此装置放在硬质木柱上，则ｌ、Ｌ、α间应当满足______________关系才能使木钉由垂直位置稍微偏斜后，此装置能以O点为支点摆动而不致倾倒．图3-12 图3-13４．如图3-13所示，长度为2Ｌ、粗细均匀的杆，一端靠在铅直的墙上，而另一端靠在不动的光滑面上．为了使杆即使没有摩擦仍能在任意位置处于平衡，试写出这个表面的横截线的函数表达式y（ｘ）(杆总是位于垂直于墙面的竖直平面内)．５．如图3-１４所示，两个质量分别为ｍ1和ｍ2的小环能沿着一光滑的轻绳滑动．绳的两端固定于直杆的两端，杆与水平线成角度θ．在此杆上又套一轻小环，绳穿过轻环并使ｍ1、ｍ2在其两边．设环与直杆的接触是光滑的，当系统平衡时，直杆与轻环两边的绳夹角为φ．试证：ｔａｎθ/ｔａｎφ＝(ｍ2－ｍ1)/(ｍ1＋ｍ2)．图3-１４图3-１５６．一根质量为ｍ的均匀杆，长为L，处于竖直的位置，一端可绕固定的水平轴转动，如图3-１５所示．有两根水平弹簧，劲度系数相同，把杆的上端拴住，如图所示，问弹簧的劲度系数ｋ为何值时才能使杆处于稳定平衡?７．如图3-１６所示，一块厚ｄ的木板位于半径为R的圆柱上，板的重心刚好在圆柱的轴上方．板与圆柱的摩擦因数为μ．试求板可以处于稳定平衡状态的条件．图3-１6 图3-１7８．用均匀材料制成的浮子，具有两个半径均为R的球冠围成的外形，像一粒豆子，如图3-１７所示．浮子的厚度ｈ＜２Ｒ，质量为ｍ1．沿浮子对称轴向浮子插入一细辐条，穿过整个厚度．辐条长ｌ＞ｈ，质量为ｍ2．当将浮子辐条向上地浸于水中时，浮子只有少部分没于水中．浮子的状态是稳定的吗?９．如图3-１８所示，儿童玩具不倒翁高ｈ＝21cm，质量ｍ＝300ｇ，相对轴ＫＤ对称分布．不倒翁的下部是半径Ｒ＝６ｃｍ的半球面，如果不倒翁放在与水平面成角度α＝３０°的粗糙面上，当它的轴KD与竖直方向倾角β＝４５°，则处于稳定平衡状态．为了使它在水平面上失去稳定平衡，试问最少需在头顶K处加多少塑泥?图3-１８１０．有一长为0.2ｍ、截面积为2ｃｍ2的均匀细棒，密度为5×102ｋｇ／ｍ3．(1)在细棒下端钉上一小铁片(不计体积)，让细棒竖立在水面，若细棒露出水面部分的长为０．０２ｍ，则小铁片质量为多少?(2)不拿去浸在水中的小铁片，在上端要截去多少长度，恰好使上端与水面齐平?(3)要使细棒竖在水面是稳定平衡，下端小铁片至少要多重?１１．两个相同长方体处于如图3-１９所示位置．问当α角为多少时它们才可能平衡?长方体与水平面间摩擦因数为μ，长方体长ｂ宽ａ．长方体间无摩擦．图3-１９图3-２０１２．如图3-２０所示，在互相垂直的斜面上放置一匀质杆AB，设各接触面的摩擦角均为φ（μ＝ｔａｎφ），求平衡时杆ＡＢ与斜面ＡＯ交角θ的范围．已知斜面BO与水平面交角为α．１３．4个半径均为R的光滑球静止于一个水平放置的半球形碗内．该4球球心恰在同一个水平面上，现将相同的第5个球放在前述4球之上，而此系统仍能维持平衡，求碗的半径为多少?参考解答１．Ｂ ２．随遇平衡 稳定平衡 不稳定平衡３．ｌｃｏｓα≥Ｌ４．因为杆是随遇平衡，重心始终在ｘ轴上，上端点坐标为ｘ＝０，下端点坐标满足ｘ2＋（２ｙ）2＝（２Ｌ）2.５．同一绳上张力处处相同设为ＦT，ｍ1、ｍ2受力且平衡如图答3-１所示，则 ＦT ＝(ｍ1ｇ)/[２ｓｉｎ（φ－θ）]＝(ｍ2ｇ)/[２ｓｉｎ（φ＋θ）]，整理可得证．图答3-１６．要成稳定平衡，应令杆偏离平衡位置一小角度Δθ时，弹力矩大于重力矩，即 2ｋ（Ｌ·Δθ）·Ｌ≥ｍｇ(Ｌ/２)·Δθ，故 ｋ＞(ｍｇ)/(４Ｌ)．图答3-２7.如图答３-２所示，板从原位置(ａ为板下沿)偏转一小角度α到毗邻位置(ａ′为板下沿)，与圆柱面切点从M移至M′，＝Ｒα，均匀板重心从Ｃ移至Ｃ′，稳定平衡条件是Ｃ′位置高于C，则有Ｒｃｏｓα＋αRｓｉｎα＋(ｄ/２)ｃｏｓα＞Ｒ＋(ｄ/２)，α很小时，有ｓｉｎα≈α， 得 ｄ＜２Ｒ，且α＜ａｒｃｔａｎμ．８．整体重心位置设为C，如图答3-３所示，ｌC＝(ｈ/２)＋ｍ2/(ｍ1＋ｍ2)（(1/２)－(ｈ/２)），偏转小角度Δθ，浮心位置不变，呈何种稳定视重心侧移后与浮心的位置关系：图3-３若ｌC＝Ｒ，ｍ1/ｍ2＝(ｌ－２Ｒ)/(２Ｒ－ｈ)时为稳定平衡；若ｌC＞Ｒ，ｍ1/ｍ2＜(ｌ－２Ｒ)/(２Ｒ－ｈ)时为不稳定平衡；若ｌC＜Ｒ，ｍ1/ｍ2＞(ｌ－２Ｒ)/(２Ｒ－ｈ)时为稳定平衡．９．整体重心设为Ｏ′，在斜面上时重力作用线过D′，如图答3-4所示，ＯＤ′与竖直方向成α角，在△ＯＤ′Ｏ′中，有Ｒ/ｓｉｎβ＝ＯＯ′/ｓｉｎα，得 ＯＯ′＝３ｃｍ；在水平面时要成稳定平衡，至少要ＯＯ′·ｍ＝Δｍ·（ｈ－Ｒ），解得 Δｍ＝84ｇ．图答3-4 图答3-５１０．(1)小铁片质量ｍ＝16ｇ （２）截去Δｘ＝4ｃｍ （３）应使浮心与质心重合或在质心之上，则[Ｍ//(Ｍ＋ｍ)]·(1/2)≤(Ｍ＋ｍ)/(2ρ水S)，解得ｍmin＝8ｇ．１１．受力情况如图答3-５所示，当α＞ａｒｃｔａｎ(ａ/ｂ)＝θ时，系统可能平衡，否则右块会右翻；当α足够大，ｆ＝μＧ时，右块满足μＧ·ｂｃｏｓα＝Ｇ·(/２)ｓｉｎ（α－θ），故 α＝ｔａｎ-1（２μ＋(ａ/ｂ)）；左块应满足 μＧ·ｂｃｏｓα＝Ｇ·(ａ/２)＝Ｇ·(/２)ｓｉｎ（α－θ），可得 ｓｉｎ（α－θ）＝(ａ/)＝ｓｉｎθ，ｔａｎ(α/２)＝(ａ/ｂ)，α＝２arctan(ａ/ｂ)；综上可得，ａｒｃｔａｎ(ａ/ｂ)＜α＜ｍｉｎ｛ａｒｃｔａｎ（２μ＋(ａ/ｂ)），２ａｒｃｔａｎ(ａ/ｂ)｝图答3-６１２．如图答3-６甲、乙、丙图分别表示杆与ＡＯ边所成角度θ＝α、θ＜α、θ＞α的情况，由甲图可知杆处于不稳定平衡，此时Ａ、Ｂ两处静摩擦力可均为零；受一微扰，若杆向ＡＯ边移动，θ角递减，如图乙所示，Ａ、Ｂ两处约束力同时达摩擦角φ0（μ＝ｔａｎφ0）时，有∠ＡＯ′Ｂ＝９０°，∵ Ｏ′Ｇ＜ＡＧ，∴ ９０°－φ0－θ＝９０°＋φ0－α，得 θ＝α－２φ0．若φ＞φ0，考虑A处约束力达摩擦角时，有∠Ｏ″ＡＧ＝９０°－φ－θ，∠ＡＯ″Ｇ＝９０°＋φ－α，∵ Ｏ″Ｇ＜ＡＧ，∴ ９０°－φ－θ＜９０°＋φ－α，得 θ＞α－２φ．同样考虑Ｂ处约束力达摩擦角时，有∠ＢＧ＝θ＋φ，∠ＢＧ＝θ＋α－（θ＋φ）＝α－φ，∵ Ｇ＞ＢＧ，∴ θ＋φ＞α－φ，亦得θ＞α－２φ．若向BO边移动，θ角递增，如图丙，A、B两处约束力同时达摩擦角φ0时，有∠ＡＯ′Ｂ＝９０°，θ＝α＋２φ0，若φ＞φ0，考虑A处约束力达摩擦角时，则有∠Ｏ″ＡＧ＝９０°＋φ－θ，∠ＡＯ″Ｇ＝９０°－φ－α，∵ Ｏ″Ｇ＞ＡＧ，∴ ９０°＋φ－θ＞９０°－φ－α，得 θ＜α＋２φ．同样考虑Ｂ处约束力达摩擦角时，有∠ＢＧ＝θ－φ，∠ＢＧ＝θ＋α－（θ－φ）＝α＋φ，∵Ｇ＜ＢＧ，∴θ－φ＜α＋φ，亦得 θ＜α＋２φ．综上得结论为α－２φ≤θ≤α＋２φ．图答3-７１３．设碗半径为ｒ，五球球心在棱长为2R的正四棱锥顶点，下四球与碗切于P，下四球接触而无挤压，球在碗中方位如图答3-7，上球对每个下球压力设为N，N＝(Ｇ/４)·，碗对下球支持力设为T，方向与竖直方向成α角，则有(Ｎ/ｓｉｎα)＝(Ｇ/ｓｉｎ（４５°－α）)，得ｔａｎα＝(１/５)，由丙图所示几何关系有(ｒ－Ｒ/ｓｉｎ４５°)＝(２Ｒ/ｓｉｎα)，得ｒmax＝（１＋２）Ｒ，ｒ增大，平衡被破坏，ｒ减小，五球方位不变，但下四球间有挤压，及至ｒ最小时，下四球恰切于碗边，如丙图所示，此时ｒmin＝ｒmaxｓｉｎα＝(２＋１/)Ｒ，综上可得，碗半径应为（１＋２)Ｒ≥ｒ≥(２+1/)Ｒ．（待续)。