艺体生复习资料--数列基础

考点三十数列的通项知识突围合抱之木,生于毫末1．数列{a n}的前n项和S nS n=a1+a2+a3+…+a n2．数列的通项a n与前n项和S n的关系a n=　S1 (n=1)S n-S n－1(n≥2)3．根据a n与a n+1(或a n与a n-1)的递推关系求通项公式(1)若已知数列的首项a1(或某一项)，且从第2项(或某一项)开始的任一项a n。

与它的前一项a n-1(或前几项)间的关系可以用一个公式来表示，那么该公式就叫作这个数列的递推公式．递推公式也是给出数列的一种方(2)数列的第n项a n与项数n之间的函数关系可以用一个公式a n=f(n)来表示，那么a n就是数列的通项公式注：①并非所有的数列都有通项公式。

②有的数列可能有不同形式的通项公式。

③数列的通项是一种特殊的函数关系式。

④注意区别数列的通项公式和递推公式几种常见的数列的通项公式的求法。

题型突围纸上得来终觉浅,绝知此事要躬行.一．公式法例1.等差数列a n是递减数列，且a2⋅a3⋅a4=48，a2+a3+a4=12，则数列的通项公式是（）A.a n=2n-12B.a n=2n+4C.a n=-2n+12D.a n=-2n+10方法总结当已知数列为等差或等比数列时，可直接利用等差或等比数列的通项公式，只需求得首项及公差公比。

【题型练1-1】(2015福建)等差数列a n中，a2=4，a4+a7=15．(Ⅰ)求数列a n的通项公式；(Ⅱ)设b n=2a n-2+n，求b1+b2+b3+⋅⋅⋅+b10的值．【题型练1-2】(2015北京)已知等差数列{a n}满足a1+a2=10，a4-a3=2．(Ⅰ)求{a n}的通项公式；(Ⅱ)设等比数列{b n}满足b2=a3，b3=a7．问：b6与数列{a n}的第几项相等？【题型练1-3】(2018全国卷Ⅲ)等比数列{a n}中，a1=1，a5=4a3．(1)求{a n}的通项公式；(2)记S n为{a n}的前n项和．若S m=63，求m．【题型练1-4】(2017新课标Ⅰ)记S n为等比数列{a n}的前n项和，已知S2=2，S3=-6．(1)求{a n}的通项公式；(2)求S n，并判断S n+1，S n，S n+2是否成等差数列。

A . 55B . 11 C. 50 D .604 . （5分）设｛a n ｝是首项为 ③，S 成等比数列，贝U a 1 = a 1,公差为-2的等差数列，S h 为前n 项和，若Si , A . 2B . - 2 C. 1 D .5. （5 分）设数列｛a n ｝前n 项和为S n ，已知“畧，己血1 5S2O 18等于(50445048 56.( 5 分)在数列｛a n ｝中,a 2=8, a 5=2,且 2a n +1 — a n +2=3n( n € N )，则 1 a 1| + | a 2|+ …+| a 1o |的值是( )A . 210B . 10 C. 50 D . 907. (5 分)已知数列｛a n ｝的前 n 项和为 S n , a 1=1, a 2=2，且 a n +2- 2a n +什a n =O(n €* 、_ ________N ),记 T n =4034 20124036 20198. （5分）在等比数列｛a n ｝中，a 3=2, a 6=16,则数列｛a n ｝的公比是（ ）A . - 2B .: C. 2 D . 49. （5分）若正项递增等比数列｛a n ｝满足1+ （a 2-却+（出-氐）=0 （众R ）,)27 D .—艺体生提分必刷题基础练习专题：数列一、选择填空：1. （5分）已知数列｛a n ｝满足 a n +i =2a n （n € N ）, a 什a 3=2,贝U a 5+a 7=（ ）A . 8 B. 16 C. 32 D . 642. （5分）已知数列｛a n ｝满足：a i =1, a n >0, a n +i 2- a n 2=1 （n € N *）,那么使 a n <5成立的n 的最大值为（）A . 4 B. 5 C. 24 D . 253. （5 分）在等差数列｛a n ｝中，若S n 为前n 项和，2为=&+5,则Sn 的值是（）C.B .)D .8E 『），则 T 2018=（C.B .则a 8+入a 的最小值为（10. （5分）已知递减等差数列｛a n ｝中，a 3=- 1, a 4为a i ,-氏等比中项，若S n为数列｛a n ｝的前n 项和，贝U S 7的值为 ________ .11. （5分）已知｛a n ｝是等比数列，若：=（a 2, 2）, b = （a 3, 3）,且7//E ，则上兰竺a 3+a 512. （5分）我国古代数学名著《张邱建算经》有 分钱问题”今有与人钱，初一 人与三钱，次一人与四钱，次一人与五钱，以次与之，转多一钱，与讫，还敛聚 与均分之，人得一百钱，问人几何？意思是：将钱分给若干人，第一人给3钱,第二人给4钱，第三人给5钱，以此类推，每人比前一人多给1钱，分完后，再 把钱收回平均分给各人，结果每人分得 100钱，问有多少人？则题中的人数是 .13. （5分）已知各项为正的等比数列｛a n ｝中，a 2a 3=16,则数列｛log 2a n ｝的前四项 和等于 . 14. （ 5 分）数列｛a n ｝满足：若 lOg 2a n +1=1+lOg 2a n , a 3=10,则 a 8= ____________ .15・（5 分）已知数列｛a n ｝满足 _ , !- _■ . : ■■: \ '，且 a 1+a 2+a 3+^+a 10=1 ,贝U log 2 （a 101+a 102+…+an 0）=_________ 16 . （5分）已知s n 是等差数列｛a n ｝的前n 项和，a 1=1,先=3&,贝U17 . （5 分）在数列｛a n ｝中，a 1=1, a 2=2, a n +1=3a n - 2a n -1 （n 》2）,则 a n__________________________________________________________________________________________________________________________________22+5 罕2 S 2S 3+、简答题1. (12分)已知正项等比数列｛a n｝满足&3&9=4氏2, a?=1.(I)求｛a n｝的通项公式；(n)记b n=2na n，求数列｛b n｝的前n项和S n.2. (12分)已知数列｛a n｝的前n项和为S n, S n=2a n - 2.(1)求数列｛a n｝的通项公式；(2)令b n=a n log2a n,求｛b n｝的前n 项和T n.3. (12分)在各项均不相等的等差数列｛a n｝中，已知a4=5,且a3,氐，a&成等比数列(1)求a n；(2)设数列｛a n｝的前n项和为记b n=门+彳，求数列｛b n｝的前n项和T n.2a n'S n4. (12分)设公差大于0的等差数列｛a n｝的前n项和为S,已知S3=15,且a1, a4, a13成等比数列，记数列 - 的前n项和为T n.a n a rri-l(I)求T n；(n)若对于任意的n € N*, tT n V a n+11恒成立，求实数t的取值范围.5. (12分)设s n是数列｛&｝的前n项和•已知a i=1, S n=2- 2a n+i.(I)求数列｛an｝的通项公式；(U)设b n= (- 1)%,求数列｛b n｝的前n项和.6. (12 分)设数列｛a n｝a n=2n- 1.(1)求数列｛a n｝的前n项和；(2)设数列｛b n｝满足b n=2入中1，求数列｛a n b n｝的n项和.7. (12 分)已知｛a n｝为等差数列，且a1+a3=8, a2+a4=12.(1)求数列｛a n｝的通项公式；(2)记的｛a n｝前n项和为S,若a1, a k, S+2成等比数列，求正整数k的值.8. (12分)已知函数f (x) =ax2+bx的图象经过(-1, 0)点，且在x=- 1处的切线斜率为-1,设数列｛比｝的前n项和S n=f (n) (n € N*).(1)求数列｛a n｝的通项公式；(2)求数列｛一——｝前n项的和T n.9. (12分)已知｛a n｝是等差数列，且a1=3, 84=12，数列｛b n｝满足3=4, b4=20, 且｛b n -a n｝为等比数列.(1)求数列｛a n｝和｛b n｝的通项公式；(2)求数列｛b n｝的前n项和S n.10- (11 12分)设数列｛an｝满足aj=l j a n|_|=：a Il+n+l (n£ N*)(1)求数列｛an｝的通项公式；(2)若数列的前n项和为Tn,求Tn.11 (12分)已知数列｛a n｝的前n项和S n=k (3n- 1),且出=27.(1)求数列｛a n｝的通项公式；(2)若b n=log3a n,求数列｛—-—｝的前n项和T n.卅Ml参考答案与解析选择填空：1.(5分)已知数列®｝满足a n+i=2a n (n€ N*), a i+a s=2,则a5+a?=( )A. 8B. 16C. 32D. 64【解答】解：•••数列｛a n｝满足a n+i=2c h (n€ N*),•••此数列是等比数列，公比为2. 则a5+a7=24 (a i+a3)=24x 2=32.故选：C.2.(5 分)已知数列｛a n｝满足：a i=1, a n > 0, a n+/ - a n2=1 (n € N，那么使a n v 5成立的n的最大值为( )A. 4B. 5C. 24D. 25【解答】解：由题意a n+12- a n2=1,二a n2为首项为1,公差为1的等差数列，••• a n2=1+ (n- 1)x 1=n，又a n>0，则a n=.丨,由a n v 5 得.| V 5,• nv 25.那么使a n V 5成立的n的最大值为24.故选C.3.(5 分)在等差数列｛a n｝中，若S n为前n项和，2为=&+5,则Sn的值是( )A. 55B. 11C. 50 D . 60【解答】解：设等差数列｛a n｝的公差为d,v 2a7=a s+5,A 2a什12d=ai+7d+5,--a1 +5d=5=a s,. ll(€i +n则01= . =11a s=55.故选：A .4 . (5分)设｛a n｝是首项为a1,公差为-2的等差数列，S n为前n项和，若S, £, St成等比数列，贝U a1=( )A . 2B . - 2 C. 1 D . - 1【解答】解: a n=d - 2 (n - 1),Si=a1, S2=2a1 - 2, S=4a1 - 12, ••• S,S4成等比数列，-I.-. J =a 1 (4a 1 -⑵,解得a i = - 1. 故选：D .•••数列｛a n ｝是以4为周期的周期数列,二 S 2oi8=504X( a i +a 2+a 3+a 4) +a i +a 2=1008+= ,55故选：B.6.( 5 分)在数列｛a n ｝中,a 2=8, a 5=2,且 2a n +i — a n +2=a n( n € N )，则 I a i | + | a 2|+ …+1 a io l的值是（ ）A . 2i0 B. i0 C. 50 D . 90【解答】 解：T 2a n +i — a n +2=a (n € N *),即 2a n +i =ai +2+a n (n € N *), •••数列｛a n ｝是等差数列，设公差为 d ,则 a i +d=8, a i +4d=2, 联立解得a i =10, d= — 2,••• a n =10 — 2 (n - 1) =12— 2n .1 255 245 5a 4=2X35=2 X4 -L 3 J- 1 -L2 =2,55553i+32+33+345. （5分）设数列｛a n ｝前n 项和为S n ,已知q二一'a n+l =二 a 2=2xS 2oi8 等于（【解答】解：；吨 C 5048.-3a 3=2 X 字令a n>0,解得nW6.S n 二 ------------- =11 n - n 2.2I a i |+| a 2|+ —+l a io | =a i +a 2+・・+a - a 7- — a io =2S 6 - Si o=2 (11X 6- 62)-( 11 X 10- 102) =50.故选：C.7. （5分）已知数列｛a n ｝的前n 项和为0,印=1, a 2=2,且心+2 N ）,记 T n =则：数列为等差数列. 设公差为 d ,则:d=c 2- a 1=2 - 1=1, 亠■i+l_2^20L8 _4036 ^OlS'^OlS-hl _20L9故选:8. （5分）在等比数列｛a n ｝中，a 3=2, a 6=16,则数列｛a n ｝的公比是（ A .- 2 B.血 C. 2 D . 4【解答】解：根据题意，等比数列｛&｝中，a 3=2, a 6=16,122! B .2018 2018【解答】解：数列｛a n ｝的前n 项和为S n , C 1 = 1, C 2=2,且C n +2*N ),A . 2017C.40362019D .2a n +1+a n =0 (n €2a n +1+a n =0 (n €CnElT),则 T 2018=()a n =1 + n — 1=n . S n =l+2+-+ii=n ^y^^■=2■〔丄S nn+1所以：0#；+盒+…宜则: 故: 则:),=2,(1今洽寺…七击), =27盏),所以:贝U q3=—=8,a3解可得q=2;故选：C.9. (5分)若正项递增等比数列｛a n｝满足1+ (a2 - d) +X( a3-a5)=0 ( X€ R), 则a8+ X a的最小值为(274A. B. c. D.)27【解答】解：设等比数列的公比为q (q> 1),1 + (a2 — a4) + X (a3 - a5) =0,可得X = -L--q(t+1 ) 3Q5-!t则设f (t)f'(t)当t > 一时，f (t)递增;当0vtv —时，f (t)递减.可得t=则a8+ X a的最小值为，此时q=」,f (t)取得最小值，且为27_:.274故选c.10.（5分）已知递减等差数列｛a n｝中，a3=- 1, a4为a i,-宪等比中项，若S为数列｛a n｝的前n项和，贝U S7的值为 -14 .【解答】解：设递减等差数列｛a n｝的公差d v0, a3=- 1, a4为a i, - a s等比中项，••• a〔+2d=- 1, 谕-a e X 印，即（哲+3d）' = -（a〔+5d）x 印，联立解得：a1=1, d=- 1.贝U #7-耳戈=-14.2故答案为：-14.11.（5分）已知｛a n｝是等比数列，若3= （a2, 2）, b = （a3, 3）,且盲//E，则竺巴|a3+a5 =2—I一色一.12.（5分）我国古代数学名著《张邱建算经》有分钱问题”今有与人钱，初一人与三钱，次一人与四钱，次一人与五钱，以次与之，转多一钱，与讫，还敛聚与均分之，人得一百钱，问人几何？意思是：将钱分给若干人，第一人给3钱, 第二人给4钱，第三人给5钱，以此类推，每人比前一人多给1钱，分完后，再把钱收回平均分给各人，结果每人分得100钱，问有多少人？则题中的人数是195 .【解答】解：设共有n人，根据题意得；3n+ ' =100n,C—■解得n=195;•••一共有195人.故答案为：195.13.（5分）已知各项为正的等比数列｛a n｝中，a283 = 16,则数列｛ log2a n｝的前四项和等于8 .【解答】解：各项为正的等比数列｛a n｝中，a2a3=16,可得a1a4=a2a3=16,即有 log 2a 什Iog 2a 2+log 2a 3+log 2a 4=log 2 （&但2&394）=Iog 2256=8.故答案为：8.14. （5 分）数列｛a n ｝满足：若 Iog 2a n +i =1+log 2a n , a 3=10,则 a 8= 320 .【解答】解:••Tog 2an +i =1+log 2a n--a n +1=2a n•••数列｛a n ｝是2为公比的等比数列a 8=a 325=320故答案为：32015・（5分）已知数列｛a n ｝满足 a^pl+lo a n Cn€ H*） ,且 a 计&2+出+…+ae=1,则 log 2 （a 101+a 102+・・+an o ） = 100 .【解答】解：t l □却迁出二1+1口岂片（口€『），•- log 2a n +1 - log 2a n =1，即:J . _'，_1 -,2 a n•数列｛a n ｝是公比q=2的等比数列.则 a 101+a 102+°・+a 110= （a 1+a 2+a 3+・・+a 1。

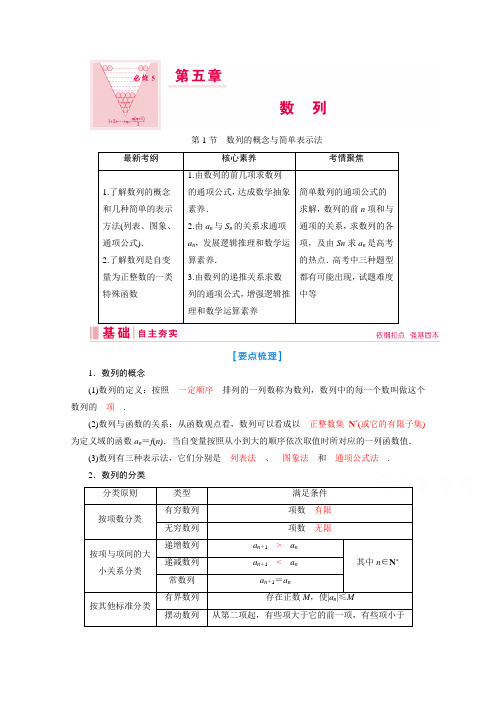
第1节 数列的概念与简单表示法最新考纲核心素养考情聚焦1.了解数列的概念和几种简单的表示方法(列表、图象、通项公式)．2.了解数列是自变量为正整数的一类特殊函数1.由数列的前几项求数列的通项公式，达成数学抽象素养．2.由a n 与S n 的关系求通项a n ，发展逻辑推理和数学运算素养．3.由数列的递推关系求数列的通项公式，增强逻辑推理和数学运算素养简单数列的通项公式的求解，数列的前n 项和与通项的关系，求数列的各项，及由Sn 求a n 是高考的热点．高考中三种题型都有可能出现，试题难度中等1．数列的概念(1)数列的定义：按照 一定顺序 排列的一列数称为数列，数列中的每一个数叫做这个数列的 项 .(2)数列与函数的关系：从函数观点看，数列可以看成以 正整数集N *(或它的有限子集) 为定义域的函数a n ＝f (n )．当自变量按照从小到大的顺序依次取值时所对应的一列函数值．(3)数列有三种表示法，它们分别是 列表法 、 图象法 和 通项公式法 . 2．数列的分类分类原则类型满足条件 按项数分类有穷数列 项数 有限 无穷数列 项数 无限按项与项间的大小关系分类递增数列a n ＋1 > a n 其中n ∈N *递减数列 a n ＋1 < a n 常数列 a n ＋1＝a n按其他标准分类有界数列存在正数M ，使|a n |≤M摆动数列从第二项起，有些项大于它的前一项，有些项小于(1)通项公式：如果数列{a n }的第n 项a n 与 序号n 之间的关系可以用一个式子 a n ＝f (n ) 来表示，那么这个公式叫做这个数列的通项公式．(2)递推公式：如果已知数列{a n }的第1项(或前几项)，且从第二项(或某一项)开始的任一项a n 与它的前一项a n －1(或前几项)间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的递推公式．4．已知数列{a n }的前n 项和S n ，则a n ＝⎩⎪⎨⎪⎧S 1 (n ＝1)， S n －S n －1 (n ≥2).1.一些常见数列的通项公式(1)数列1,2,3,4，…的通项公式为a n ＝n ； (2)数列2,4,6,8，…的通项公式为a n ＝2n ； (3)数列1,3,5,7，…的通项公式为a n ＝2n －1； (4)数列1,2,4,8，…的通项公式为a n ＝2n －1； (5)数列1,4,9,16，…的通项公式为a n ＝n 2； (6)数列1，12，13，14，…的通项公式为a n ＝1n .(7)数列1，－1,1，－1，…的通项公式为a n ＝(－1)n －1或(－1)n ＋1；(8)数列－1,1，－1,1，…的通项公式为a n ＝(－1)n . 2．典型的递推数列及处理方法其中(1)n ＋1n n ＋1n n ＋1＝pa n ＋pλ－λ，与a n ＋1＝pa n ＋q 比较即可知只要λ＝qp －1.(2)a n ＋1＝pa n ＋q ·p n ＋1(p ≠0,1，q ≠0)的求解方法是两端同时除以p n ＋1，即得a n ＋1p n ＋1－a np n＝q ，数列⎩⎨⎧⎭⎬⎫a n p n 为等差数列．[思考辨析]判断下列说法是否正确，正确的在它后面的括号里打“√”，错误的打“×”． (1)1,1,1,1，…不能构成一个数列．( )(2)任何一个数列不是递增数列，就是递减数列．( ) (3)所有数列的第n 项都能使用公式表达．( )(4)根据数列的前几项归纳出的数列的通项公式可能不止一个．( )(5)已知a n ＋2＝f (a n ＋1，a n )时，如果要确定这个数列，则必须知道初始值a 1，a 2.( ) (6)如果数列{a n }的前n 项和为S n ，则对∀n ∈N *，都有a n ＋1＝S n ＋1－S n .( ) 答案：(1)× (2)× (3)× (4)√ (5)√ (6)√ [小题查验]1．(·长沙市模拟)已知数列的前4项为2,0,2,0，则依此归纳该数列的通项不可能是( ) A ．a n ＝(－1)n －1＋1B ．a n ＝⎩⎪⎨⎪⎧2，n 为奇数，0，n 为偶数C ．a n ＝2sin n π2D ．a n ＝cos(n －1)π＋1解析：C [对n ＝1,2,3,4进行验证，a n ＝2sin n π2不合题意，故选C.]2．已知数列的通项公式为a n ＝n 2－8n ＋15，则3( ) A ．不是数列{a n }中的项 B ．只是数列{a n }中的第2项 C ．只是数列{a n }中的第6项 D ．是数列{a n }中的第2项和第6项 解析：D [令a n ＝n 2－8n ＋15＝3， 整理可得n 2－8n ＋12＝0， 解得n ＝2或n ＝6.故3是数列{a n }中的第2项或第6项，故选D.] 3．设数列{a n }的前n 项和S n ＝n 2，则a 8的值为( ) A ．15 B ．16 C ．49D ．64解析：A [∵S n ＝n 2，∴a 1＝S 1＝1.当n ≥2时，a n ＝S n －S n －1＝n 2－(n －1)2＝2n －1. ∴a n ＝2n －1，∴a 8＝2×8－1＝15.]4．(人教B 版教材例题改编)已知函数f (x )＝x －1x ，设a n ＝f (n )(n ∈N *)，则{a n }是________数列(填“递增”或“递减”)．答案：递增5．在数列{a n }中，a 1＝1，a n ＋2＝a n ＋1－a n (n ∈N *)，则a 100等于________． 解析：因为a n ＋2＝a n ＋1－a n ，所以a n ＋3＝a n ＋2－a n ＋1. 两式相加得a n ＋3＝－a n ，则a n ＋6＝－a n ＋3＝a n ，即数列{a n }的周期为6，所以a 100＝a 16×6＋4＝a 4＝a 3－a 2＝(a 2－a 1)－a 2＝－a 1＝－1. 答案：－1考点一 由数列的前几项求数列的通项公式(自主练透)[题组集训]1．已知n ∈N *，给出4个表达式：①a n ＝⎩⎪⎨⎪⎧0，n 为奇数，1，n 为偶数，②a n ＝1＋(－1)n 2，③a n ＝1＋cos n π2，④a n ＝⎪⎪⎪⎪sin n π2.其中能作为数列：0,1,0,1,0,1,0,1，…的通项公式的是( )A ．①②③B ．①②④C ．②③④D ．①③④解析：A [检验知①②③都是所给数列的通项公式．] 2．根据数列的前几项，写出各数列的一个通项公式： (1)4,6,8,10，…； (2)－11×2，12×3，－13×4，14×5，…； (3)1,0,1,0，…； (4)9,99,999,9 999，….解：(1)各数都是偶数，且最小为4，所以通项公式 a n ＝2(n ＋1)，n ∈N *.(2)这个数列的前4项的绝对值都等于序号与序号加1的积的倒数，且奇数项为负，偶数项为正，所以它的一个通项公式a n ＝(－1)n ×1n (n ＋1)，n ∈N *.(3)这是一个摆动数列，奇数项是1，偶数项是0，所以此数列的一个通项公式a n ＝⎩⎪⎨⎪⎧1，n 为奇数，0，n 为偶数.或 a n ＝(－1)n ＋112＋12，n ∈N *.(4)这个数列的前4项可以写成10－1,100－1,1 000－1,10 000－1，所以它的一个通项公式a n ＝10n －1，n ∈N *.用观察法求数列的通项公式的技巧(1)根据数列的前几项求它的一个通项公式，要注意观察每一项的特点，观察出项与n 之间的关系、规律，可使用添项、通分、分割等办法，转化为一些常见数列的通项公式来求．对于正负符号变化，可用(－1)n 或(－1)n ＋1来调整．(2)根据数列的前几项写出数列的一个通项公式是不完全归纳法，它蕴含着“从特殊到一般”的思想．[提醒] 不是所有的数列都有通项公式，若有，也不一定唯一．考点二 由a n 与S n 的关系求通项a n (师生共研)[典例] (1)(·全国Ⅰ卷) 记S n 为数列{a n }的前n 项和．若S n ＝2a n ＋1，则S 6＝_____________. (2) 若数列{a n }的前n 项和S n ＝3n ＋2n ＋1，则{a n }的通项公式是a n ＝________. [解析] (1) 根据S n ＝2a n ＋1，可得S n ＋1＝2a n ＋1＋1， 两式相减得a n ＋1＝2a n ＋1－2a n ，即a n ＋1＝2a n ， 当n ＝1时，S 1＝a 1＝2a 1＋1，解得a 1＝－1，所以数列{a n }是以－1为首项，以2为公比的等比数列， 所以S 6＝－(1－26)1－2＝－63.(2) 因为当n ＝1时，a 1＝S 1＝6；当n ≥2时，a n ＝S n －S n －1＝(3n ＋2n ＋1)－[3n －1＋2(n －1)＋1]＝2·3n －1＋2， 由于a 1不适合此式，所以a n ＝⎩⎪⎨⎪⎧6，n ＝1，2·3n －1＋2，n ≥2.[答案] (1)－63 (2) ⎩⎪⎨⎪⎧6，n ＝1，2·3n －1＋2，n ≥2.已知S n 求a n 时应注意的问题(1)应重视分类讨论思想的应用，分n ＝1和n ≥2两种情况讨论；特别注意a n ＝S n －S n －1中需n ≥2.(2)由S n －S n －1＝a n 推得a n ，当n ＝1时，a 1也适合“a n 式”，则需统一“合写”． (3)由S n －S n －1＝a n ，推得a n ，当n ＝1时，a 1不适合“a n 式”，则数列的通项公式应分段表示(“分写”)，即a n ＝⎩⎪⎨⎪⎧S 1(n ＝1)S n －S n －1(n ≥2).提醒：在利用数列的前n 项和求通项时，往往容易忽略先求出a 1，而是直接把数列的通项公式写成a n ＝S n －S n －1的形式，但它只适用于n ≥2的情形．[跟踪训练]1．已知数列{a n }的前n 项和S n ＝2n 2－3n ，则{a n }的通项公式为________． 解析：a 1＝S 1＝2－3＝－1，当n ≥2时，a n ＝S n －S n －1＝(2n 2－3n )－[2(n －1)2－3(n －1)]＝4n －5，由于a 1也适合此等式，∴a n ＝4n －5.答案：a n ＝4n －52．已知数列{a n }的前n 项和S n 满足S n ＝3n ＋b ，则a n ＝________. 解析：a 1＝S 1＝3＋b ，当n ≥2时，a n ＝S n －S n －1＝(3n ＋b )－(3n －1＋b ) ＝2·3n －1.当b ＝－1时，a 1适合此等式．当b ≠－1时，a 1不适合此等式． ∴当b ＝－1时，a n ＝2·3n －1；当b ≠－1时，a n ＝⎩⎪⎨⎪⎧3＋b ，n ＝1，2·3n －1，n ≥2.答案：⎩⎪⎨⎪⎧3＋b ，n ＝1，2·3n －1，n ≥2.考点三 由数列的递推关系求数列的通项公式(多维探究)[命题角度1] 形如a n ＋1＝a n ＋f (n )，求a n1．(1)在数列{a n }中，a 1＝2，a n ＋1＝a n ＋1n (n ＋1)，求数列{a n }的通项公式．(2)若数列{a n }满足：a 1＝1，a n ＋1＝a n ＋2n ，求数列{a n }的通项公式． 解：(1)由题意，得a n ＋1－a n ＝1n (n ＋1)＝1n －1n ＋1， a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1＝⎝ ⎛⎭⎪⎫1n －1－1n ＋⎝ ⎛⎭⎪⎫1n －2－1n －1＋…＋⎝⎛⎭⎫12－13＋⎝⎛⎭⎫1－12＋2＝3－1n . (2)由题意知a n ＋1－a n ＝2n ，a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1 ＝2n －1＋2n －2＋…＋2＋1＝1－2n1－2＝2n －1. [命题角度2] 形如a n ＋1＝a n f (n )，求a n2．在数列{a n }中，a 1＝1，前n 项和S n ＝n ＋23a n .求数列{a n }的通项公式．解：由题设知，a 1＝1.当n ≥2时，a n ＝S n －S n －1＝n ＋23a n －n ＋13a n －1.∴a n a n －1＝n ＋1n －1. ∴a na n －1＝n ＋1n －1，…，a 4a 3＝53，a 3a 2＝42，a 2a 1＝3.将以上n －1个式子的等号两端分别相乘，得到a n a 1＝n (n ＋1)2.又∵a 1＝1，∴a n ＝n (n ＋1)2.[命题角度3] 形如a n ＋1＝Aa n ＋B (A ≠0且A ≠1)，求a n3．已知数列{a n }满足a 1＝1，a n ＋1＝3a n ＋2，求数列{a n }的通项公式． 解：∵a n ＋1＝3a n ＋2，∴a n ＋1＋1＝3(a n ＋1)，∴a n ＋1＋1a n ＋1＝3，∴数列{a n ＋1}为等比数列，公比q ＝3， 又a 1＋1＝2，∴a n ＋1＝2·3n －1，∴a n ＝2·3n －1－1.[命题角度4] 形如a n ＋1＝Aa nBa n ＋C(A ，B ，C 为常数)，求a n4．已知数列{a n }中，a 1＝1，a n ＋1＝2a na n ＋2，求数列{a n }的通项公式．解：∵a n ＋1＝2a na n ＋2，a 1＝1，∴a n ≠0，∴1a n ＋1＝1a n ＋12，即1a n ＋1－1a n ＝12，又a 1＝1，则1a 1＝1，∴⎩⎨⎧⎭⎬⎫1a n 是以1为首项，12为公差的等差数列．∴1a n ＝1a 1＋(n －1)×12＝n 2＋12，∴a n ＝2n ＋1(n ∈N *)．由数列的递推公式求通项公式时，若递推关系为a n ＋1＝a n ＋f (n )或a n ＋1＝f (n )·a n ，则可以分别通过累加、累乘法求得通项公式，另外，通过迭代法也可以求得上面两类数列的通项公式，(如角度1)．注意：有的问题也可利用构造法，即通过对递推式的等价变形，(如角度3、4)转化为特殊数列求通项.1．已知数列1，3，5，7，…，2n －1，则35是它的( ) A ．第22项 B ．第23项 C ．第24项D ．第28项 解析：B [观察知已知数列的通项公式是a n ＝2n －1，令a n ＝2n －1＝35＝45，得n ＝23.]2．数列{a n }的前n 项和为S n ，若a 1＝1，a n ＋1＝3S n (n ≥1)，则a 6等于( ) A ．3×44 B ．3×44＋1 C ．45D ．45＋1解析：A [当n ≥1时，a n ＋1＝3S n ，则a n ＋2＝3S n ＋1， ∴a n ＋2－a n ＋1＝3S n ＋1－3S n ＝3a n ＋1，即a n ＋2＝4a n ＋1， ∴该数列从第二项开始是以4为公比的等比数列．又a 2＝3S 1＝3a 1＝3，∴a n ＝⎩⎪⎨⎪⎧1 (n ＝1)，3×4n －2(n ≥2).∴当n ＝6时，a 6＝3×46－2＝3×44.]3．(·聊城市模拟)大衍数列，来源于《乾坤谱》中对易传“大衍之数五十”的推论．主要用于解释中国传统文化中的太极衍生原理．数列中的每一项，都代表太极衍生过程中，曾经经历过的两仪数量总和．是中华传统文化中隐藏着的世界数学史上第一道数列题．其前10项依次是0、2、4、8、12、18、24、32、40、50…，则此数列第20项为( )A ．180B ．200C ．128D ．162解析：B [由0、2、4、8、12、18、24、32、40、50…， 可得偶数项的通项公式：a 2n ＝2n 2. 则此数列第20项＝2×102＝200.]4．(·咸阳市二模)已知正项数列{a n } 中，a 1＋a 2＋…＋a n ＝n (n ＋1)2(n ∈N *)，则数列{a n }的通项公式a n ＝( )A ．nB ．n 2C.n2D.n 22解析：B [∵a 1＋a 2＋…＋a n ＝n (n ＋1)2，∴a 1＋a 2＋…＋a n －1＝n (n －1)2(n ≥2)，两式相减得a n ＝n (n ＋1)2－n (n －1)2＝n ，∴a n ＝n 2，(n ≥2)．又当n ＝1时，a 1＝1×22＝1，∴a n ＝n 2.n ∈N *.故选B.]5．已知数列{a n }的通项公式为a n ＝⎝⎛⎭⎫49n －1－⎝⎛⎭⎫23n －1，则数列{a n }( ) A ．有最大项，没有最小项 B ．有最小项，没有最大项 C ．既有最大项又有最小项 D ．既没有最大项也没有最小项解析：C [∵数列{a n }的通项公式为a n ＝⎝⎛⎭⎫49n －1－⎝⎛⎭⎫23n －1，令t ＝⎝⎛⎭⎫23n －1，t ∈(0,1]，t 是减函数，则a n ＝t 2－t ＝⎝⎛⎭⎫t －122－14， 由复合函数单调性知a n 先递减后递增． 故有最大项和最小项，选C.]6．(·唐山市一模)设数列{a n }的前n 项和为S n ，且S n ＝a 1(4n －1)3，若a 4＝32，则a 1＝________.解析：∵S n ＝a 1(4n －1)3，a 4＝32，∴a 4＝S 4－S 3＝255a 13－63a 13＝32，∴a 1＝12.答案：127．已知数列{a n }的前n 项和S n ＝n 2－9n ，第k 项满足5＜a k ＜8，则k 的值为________． 解析：∵S n ＝n 2－9n ，∴n ≥2时，a n ＝S n －S n －1＝2n －10，a 1＝S 1＝－8适合上式，∴a n ＝2n －10(n ∈N *)， ∴5＜2k －10＜8，得7.5＜k ＜9.∴k ＝8. 答案：88．数列 {a n }满足 a n ＋1＝11－a n ，a 8＝2，则a 1 ＝________.解析：将a 8＝2代入a n ＋1＝11－a n ，可求得a 7＝12；再将a 7＝12代入a n ＋1＝11－a n ，可求得a 6＝－1；再将a 6＝－1代入a n ＋1＝11－a n ，可求得a 5＝2；由此可以推出数列{a n }是一个周期数列，且周期为3，所以a 1＝a 7＝12.答案：129．数列{a n }的通项公式是a n ＝n 2－7n ＋6. (1)这个数列的第4项是多少？(2)150是不是这个数列的项？若是这个数列的项，它是第几项？ (3)该数列从第几项开始各项都是正数？ 解：(1)当n ＝4时，a 4＝42－4×7＋6＝－6. (2)令a n ＝150，即n 2－7n ＋6＝150，解得n ＝16或n ＝－9(舍)， 即150是这个数列的第16项．(3)令a n ＝n 2－7n ＋6＞0，解得n ＞6或n ＜1(舍)． ∴从第7项起各项都是正数．10．已知数列{a n }的前n 项和为S n ，且S n ＝32a n －1(n ∈N *)． (1)求数列{a n }的通项公式；(2)在数列{b n }中，b 1＝5，b n ＋1＝b n ＋a n ，求数列{b n }的通项公式．解：(1)当n ＝1时，S 1＝a 1＝32a 1－1，所以a 1＝2. 由S n ＝32a n －1，① 可知当n ≥2时，S n －1＝32a n －1－1，② ①－②，得a n ＝⎝⎛⎭⎫32a n －1－⎝⎛⎭⎫32a n －1－1， 所以a n ＝3a n －1，又a 1≠0，故a n －1≠0，所以a n a n －1＝3， 故数列{a n }是首项为2，公比为3的等比数列， 所以a n ＝2·3n －1.(2)由(1)知b n ＋1＝b n ＋2·3n －1. 当n ≥2时，b n ＝b n －1＋2·3n －2， …，b 3＝b 2＋2·31，b 2＝b 1＋2·30，将以上n －1个式子相加并整理， 得b n ＝b 1＋2×(3n －2＋…＋31＋30)＝5＋2×1－3n －11－3＝3n －1＋4.当n＝1时，31－1＋4＝5＝b1，所以b n＝3n－1＋4(n∈N*)．。

第12讲 数列【基础知识】1、等差数列与等比数列：11()(1)22n n a a n n na d ⎪⎪⎨-=1(1a ()ma n m da m a a a a q p n +=++=+时，pq 时，2、n a 与n S 的关系：1121(1)(2)n n n nn S n S a a a a S S n -=⎧=++⋯⇔=⎨-≥⎩【基础训练】1、（2013·重庆高考文科）若2、a 、b 、c 、9成等差数列，则c a -= ．2、（2013·北京高考文科）若等比数列{a n }满足a 2＋a 4=20，a 3＋a 5=40，则公比q = ；前n 项和S n = .3（2013·广东高考文科）设数列{}n a 是首项为1，公比为2-的等比数列，则1234||||a a a a +++= 4、（2013·四川高考文科）在等比数列{}n a 中，212a a -=，且22a 为13a 和3a 的等差中项，求数列{}n a 的首项、公比及前n 项和。

【典例分析】1．（2013·安徽高考文科）设S n 为等差数列｛a n ｝的前n 项和，837=4,2S a a ，则a 9=（ ）A.-6B.-4C.-2D.2 2．（2013·新课标Ⅰ高考文科）设首项为1，公比为23的等比数列｛a n ｝的前n 项和为S n ，则（ ）A.12-=n n a SB. 23-=n n a SC. n n a S 34-=D. n n a S 23-=3．（2013·全国卷高考文科）已知数列{}n a 满足{}12430,,103n n n a a a a ++==-则的前项和等于（ ）A.()-10-61-3B.()-1011-39C.()-1031-3D.()-1031+34．（2013·湖南高考文科·Ｔ19）设n S 为数列{n a }的前项和，已知01≠a ，2n n S S a a ⋅=-11，∈n N *(Ⅰ)求1a ，2a ，并求数列｛n a ｝的通项公式；(Ⅱ) 求数列｛n na ｝的前n 项和。

考点6 数列求通项[玩前必备]1．等差等比数列求a n的方法列关于首项和公差或公比的方程組.2．数列的前n项和S n，求a n的方法(1)第一步，令n=1,求出a1＝S1；(2)第二步，当n≥2时，求a n＝S n－S n－1；(3)第三步，检验a1是否满足n≥2时得出的a n，如果适合，那么将a n用一个式子表示；假设不适合，将a n 用分段形式写出。

3．a n与S n的关系式，求a n的方法(1)第一步，令n=1,求出a1＝S1；(2)第二步，当n≥2时，根据已有a n与S n的关系式，令n＝n＋1(或n＝n－1)，再写出一个a n+1与S n+1(或a n与S n－1)的关系式，然后两式相减，利用公式a n＝S n－S n－1消去S n，得出a n与a n+1(或a n与a n－1)的关系式，－1从而确定数列{a n}是等差数列、等比数列或其他数列，然后求出通项公式。

4．累加法求通项5. 累乘法求通项[玩转典例]题型一由数列的前n项和S n求数列的通项例1下面数列{a n}的前n项和S n，求{a n}的通项公式：(1)S n＝2n2－3n；(2)S n＝3n＋b.(3)数列{a n}满足a1＋2a2＋3a3＋…＋na n＝2n，那么a n＝.例2 (2018全国卷Ⅰ)记n S 为数列{}n a 的前n 项和，假设21n n S a =+，那么6S =_____．例3 (2015·新课标全国卷Ⅰ)S n 为数列{a n }的前n 项和．a n >0，a 2n ＋2a n ＝4S n ＋3. (1)求{a n }的通项公式；(2)设b n ＝1a n a n ＋1，求数列{b n }的前n 项和．[玩转跟踪]1．数列{a n }的前n 项和S n ＝3n 2－2n ＋1，那么其通项公式为________________．2.〔2020·福建省泉州市高三质检〔理〕〕记n S 为数列{}n a 的前n 0n a >，2634n n n S a a =+-.〔1〕求{}n a 的通项公式；〔2〕设2211n n n n n a a b a a +++=，求数列{}n b 的前n 项和n T .3.(2019衡水2调〕数列{}n a 满足：211231333()3n n n a a a a n N -*+++++=∈. 〔1〕求数列{}n a 的通项公式；题型二 利用累加法例4 (2015·江苏)设数列{a n }满足a 1＝1，且a n ＋1－a n ＝n ＋1(n ∈N *)，那么数列⎩⎨⎧⎭⎬⎫1a n 前10项的和为________.[玩转跟踪]1．数列{a n }中，a 1＝3，a 2＝5，其前n 项和S n 满足S n ＋S n －2＝2S n －1＋2n -1 (n ≥3)，试求数列{a n }的通项公式.题型三 利用累乘法例5 数列{a n }满足：a 1＝1,2n －1a n ＝a n －1(n ∈N 且n ≥2)，那么数列{a n }的通项公式是____________.[玩转跟踪]1.〔2020•眉山模拟〕数列{}n a 的前n 项和为n S ，且14121n n S a n +-=-，11a =，*n N ∈，那么{}n a 的通项公式(n a = )A ．nB ．1n +C ．21n -D ．21n +题型四 证明等差等比求通项例6 〔2020·江西省名高三第二次大联考〔理〕〕首项为4的数列{}n a 满足11221n n n na a n +++=+. 〔1〕证明：数列2n n na ⎧⎫⎨⎬⎩⎭是等差数列.〔2〕令2log n n b a =，求数列{}n b 的前n 项和n S .[玩转跟踪]1.〔2020届山东省济宁市第一中学高三二轮检测〕数列{}n a 中，11a =，121n n a a n +=+-，n n b a n =+. 〔1〕求证：数列{}n b 是等比数列; 〔2〕求数列{}n a 的前n 项和n S .[玩转练习]1．(2020·三明质检)假设S n 为数列{a n }的前n 项和，且S n ＝2a n －2，那么S 8等于( ) A ．255 B ．256 C ．510 D ．511 2．(2020·长春五校模拟)数列{a n }的前n 项和S n ＝n 2＋2n ，那么数列⎩⎨⎧⎭⎬⎫1a n ·a n ＋1的前6项和为( )A.215B.415C.511D.10113. 如果数列{a n }的前n 项和S n ＝32a n －3，那么这个数列的通项公式是( )A ．a n ＝2(n 2＋n ＋1)B ．a n ＝3·2nC ．a n ＝3n ＋1D ．a n ＝2·3n 4．数列{a n }的前n 项和为S n ，a 1＝1，S n ＝2a n ＋1，那么S n ＝( ) A ．2n －1 B ．(32)n －1 C ．(23)n －1 D ．12n －15．设数列{a n }的前n 项和S n ＝n 2，那么a 8的值为( ) A ．15 B ．16 C ．49 D ．64 6.〔2020•涪城区校级模拟〕数列{}n a 中，12a =，21a =，且满足11112(2)111n n n n a a a -++=+++，那么(n a = )A ．51nn -+ B ．22n -C ．3n -D ．62n + 7．假设数列{a n }满足a 1＝1，a n ＋1＝2n a n ，那么数列{a n }的通项公式a n ＝________. 8．在数列{a n }中，a 1＝1，a n ＋1－a n ＝2n ＋1，那么数列的通项a n ＝________. 9．S n 为正项数列{a n }的前n 项和，且满足S n ＝12a 2n ＋12a n (n ∈N *)．(1)求a 1，a 2，a 3，a 4的值； (2)求数列{a n }的通项公式．10．数列{a n }满足a 1＝1，a n ＋1＝2a n ＋1(n ∈N *)．(1)求证：数列{a n ＋1}是等比数列，并写出数列{a n }的通项公式；(2)假设数列{b n }满足114b -·214b -·314b - (1)4n b -＝(a n ＋1)n ，求数列{b n }的前n 项和S n .11.〔2020•福清市一模〕数列{}n a 的前n 项和为n S ，满足22n n a S -=．〔Ⅰ〕求n a〔Ⅱ〕假设数列{}n b 满足*14()nn n n a b n N S S +=∈，{}n b 的前n 项和n T ．12．〔2020•邵阳一模〕正项数列{}n a 中，11a =，2211230n n n n a a a a ++--=．〔1〕求数列{}n a 的通项公式；〔2〕假设数列{}n n b a -是等差数列，且12b =，314b =，求数列{}n b 的前n 项和n S ．。

高三文科数学专题复习——数列专题高中数列知识点总结1. 等差数列的定义与性质定义：1n n a a d +-=（d 为常数）， 通项：()11n a a n d =+-等差中项：x A y ，，成等差数列2A x y ⇔=+ 前n 项和()()11122n n a a n n n S nad +-==+性质：{}n a 是等差数列（1）若m n p q +=+，则m n p q a a a a +=+；（2）232n n n n n S S S S S --，，……仍为等差数列，公差为d n 2； ( 3)项数为偶数n 2的等差数列{}n a ，有nd S S =-奇偶，. .2. 等比数列的定义与性质定义：1n na q a +=（q 为常数，0q ≠）， 通项：11n n a a q -=.等比中项：x G y 、、成等比数列2G xy ⇒=，前n 项和：()11(1)1(1)1n n na q S a q q q =⎧⎪=-⎨≠⎪-⎩（要注意！）性质：{}n a 是等比数列（1）若m n p q +=+，则m n p q a a a a =··（2）232n n n n n S S S S S --，，……仍为等比数列,公比为n q .注意：由n S 求n a 的方法1n =时，11a S =； 2n ≥时，1n n n a S S -=-.1、若数列{}n a 的递推公式是251+=+n n a a ，11=a ，则它的通项公式为_____ ________，求和公式为_______________。

2、若数列{}n a 的递推公式是n n a a 311=+，311=a ，则它的通项公式为________________，求和公式为_______________。

3、若数列{}n a 的求和公式是n n S n 482-=，则它的通项公式为________ ________。

高三文科数学专题复习——数列专题高中数列知识点总结1. 等差数列的定义与性质定义：1n n a a d +-=（d 为常数）， 通项：()11n a a n d =+-等差中项：x A y ，，成等差数列2A x y ⇔=+ 前n 项和()()11122n n a a n n n S nad +-==+性质：{}n a 是等差数列（1）若m n p q +=+，则m n p q a a a a +=+；（2）232n n n n n S S S S S --，，……仍为等差数列，公差为d n 2； ( 3)项数为偶数n 2的等差数列{}n a ，有nd S S =-奇偶，..2. 等比数列的定义与性质定义：1n na q a +=（q 为常数，0q ≠）， 通项：11n n a a q -=.等比中项：x G y 、、成等比数列2G xy ⇒=，前n 项和：()11(1)1(1)1n n na q S a q q q=⎧⎪=-⎨≠⎪-⎩（要注意！）性质：{}n a 是等比数列（1）若m n p q +=+，则mn p q a a a a =··（2）232n n n n n S S S S S --，，……仍为等比数列,公比为n q .注意：由n S 求n a 的方法1n =时，11a S =； 2n ≥时，1n n n a S S -=-.1、若数列{}n a 的递推公式是251+=+n n a a ，11=a ，则它的通项公式为_____ ________， 求和公式为_______________。

2、若数列{}n a 的递推公式是n n a a 311=+，311=a ，则它的通项公式为________________， 求和公式为_______________。

3、若数列{}n a 的求和公式是n n S n 482-=，则它的通项公式为________ ________。

数列基础知识一、等差数列与等比数列二、数列的项n a 与前n 项和n S 的关系：11(1)(2)n n n s n a s s n -=⎧=⎨-≥⎩课本题1．等差数列{}n a 前n 项之和为n S ，若31710a a -=，则19S 的值为 。

952．已知数列{}n a 中，3,6011+=-=+n n a a a ，那么||||||3021a a a +++ 的值为 。

765 3．等差数列{}n a 中，01>a ，且13853a a =，则}{n S 中最大项为 。

204．已知一个等差数列前五项的和是120，后五项的和是180，又各项之和是360，则此数列共有 项。

12 5．设等比数列{}n a 中，每项均是正数，且8165=a a ，则 =+++1032313log log log a a a 20 6．设331)(+=x x f ，利用课本中推导等差数列前n 项和的公式的方法，可求得：)13()12()11()0()10()11()12(f f f f f f f ++++++-+-+- 的值为 137．已知数列{}n a 的通项12)12(-⋅+=n n n a ，前n 项和为n S ，则n S = ( 2n-1)2n+13 。

8．数列{}n a 中，)2(112,1,21121≥+===-+n a a a a a n n n ，则其通项公式为=n a n2 。

P32习题5（2）; P37练习5; P39习题7，12; P41练习4; P45习题2（1），7，12，13; P48练习2（2）; P51例4，练习2；P5习题10；P55练习4；P58习题4，6，7；P62复习题4，7，8 高考题1.已知等差数列{}n a 满足244a a +=，3510a a +=，则它的前10项的和10S = 952.已知数列{}n a 对任意的*p q ∈N ，满足p q p q a a a +=+，且26a =-，那么10a 等于 -303.已知等比数列()n a 中21a =，则其前3项的和3S 的取值范围是 (][),13,-∞-+∞4.若等差数列{}n a 的前5项和525S =，且23a =，则7a = 135.在数列{}n a 中，12a =， 11ln(1)n n a a n+=++，则n a = 2ln n +6.已知{}n a 是等差数列，124a a +=，7828a a +=，则该数列前10项和10S 等于 1007.记等差数列{}n a 的前n 项和为n S ，若112a =，420S =，则6S = 48 8.已知{}n a 是等比数列，41252==a a ，，则13221++++n n a a a a a a = 332（n --41）9.设等比数列{}n a 的公比2q =，前n 项和为n S ，则42S a = 15210.将全体正整数排成一个三角形数阵：1 2 3 4 5 6 7 8 9 10． ． ． ． ． ． ．按照以上排列的规律，第n 行（n ≥3）从左向右的第3 个数为 ．262n n -+11.已知函数()2x f x =,等差数列{}x a 的公差为2.若246810()4f a a a a a ++++=,则212310log [()()()()]f a f a f a f a ⋅⋅⋅= . －612.设S n =是等差数列{a n }的前n 项和，a 12=-8,S 9=-9,则S 16= .-7213.设数列{}n a 的前n 项和为n S ．已知1a a =，13n n n a S +=+，*n ∈N ． （Ⅰ）设3nn n b S =-，求数列{}n b 的通项公式；（Ⅱ）若1n n a a +≥，*n ∈N ，求a 的取值范围．（Ⅰ）依题意，113n n n n n S S a S ++-==+，即123n n n S S +=+，由此得1132(3)n nn n S S ++-=-． 因此，所求通项公式为13(3)2n n n n b S a -=-=-，*n ∈N ．（Ⅱ）由①知13(3)2n n n S a -=+-，*n ∈N ，于是，当2n ≥时，1n n n a S S -=-1123(3)23(3)2n n n n a a ---=+-⨯---⨯1223(3)2n n a --=⨯+-，12143(3)2n n n n a a a --+-=⨯+-22321232n n a --⎡⎤⎛⎫=+-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦， 当2n ≥时，21312302n n n a a a -+⎛⎫⇔+- ⎪⎝⎭≥≥9a ⇔-≥．又2113a a a =+>．综上，所求的a 的取值范围是[)9-+∞，．。