当前位置：文档之家 › 机械设计中的约束问题

机械设计中的约束问题

  • 格式：ppt
  • 大小：610.50 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

机械系统优化设计中的约束与优化问题

机械系统优化设计中的约束与优化问题

机械系统优化设计中的约束与优化问题在机械工程领域，优化设计是一项关键任务。

通过对机械系统进行优化，可以提高效率、减小能耗、延长使用寿命等。

然而，在进行机械系统的优化设计时，我们必须面对各种约束和优化问题。

首先，机械系统的约束可以分为两类：设计约束和工程约束。

设计约束包括机械系统的形状、尺寸、重量等方面的限制，以及与其他系统或部件的接口要求。

这些约束是设计者必须遵守的，因为它们直接关系到机械系统的可用性和实际应用。

另一方面，工程约束包括材料强度、制造成本、可维护性等因素。

这些约束是实际工程实施时需要考虑的，因为它们关系到机械系统的可靠性和经济效益。

在优化设计中，我们通常会面临多个冲突的目标。

例如，在减小机械系统的重量的同时，要确保其强度不下降；在提高机械系统的效率的同时，要保持其成本可控。

这就引入了多目标优化问题。

多目标优化问题需要寻找一个最佳的折中方案，将各个目标在不同约束条件下进行优化，以求达到最大化总体效益的目标。

为了解决这些优化问题，我们通常使用数学建模和优化方法。

对于约束问题，我们可以使用约束优化方法，如拉格朗日乘子法和KKT条件等。

这些方法通过引入拉格朗日乘子来将约束条件融入优化问题中，从而将原问题转化为一个无约束问题。

然后，我们可以使用一般的优化算法，如梯度下降、遗传算法等，来解决这个无约束问题。

此外，在实际的机械系统优化设计中，我们还会面临一些实际的限制。

例如，制造设备和制造工艺的限制，材料的可获得性等。

这些实际限制需要考虑在内，以确保设计方案的可行性和可实施性。

另一个重要问题是机械系统的不确定性。

在机械系统的设计过程中，我们通常会面临各种形式的不确定性，如设计参数的不确定性、负载的不确定性等。

这些不确定性会对设计结果产生影响，因此需要在优化设计中进行考虑。

一种常见的方法是使用鲁棒优化方法，通过考虑不确定性的范围和分布，寻找一个鲁棒的设计方案，以确保在不同的不确定条件下系统仍然能够正常工作。

机械优化设计约束优化方法

机械优化设计约束优化方法
根据求解方式的不同，约束优化设计问题可分为:直接 解法、间接解法。
（1）直接法
直接法包括：网格法、复合形法、随机试验法、 随机方向法、可变容差法和可行方向法。
（2）间接法
间接法包括：罚函数法（内点罚函数法、外点罚 函数法、混合罚函数法）、广义乘子法、广义简约梯 度法和约束变尺度法等。
直接解法通常适用于仅含不等式约束的问题，思路是
如前所述，在求解无约束问题的单纯形法中，不 需计算目标函数的梯度，而是靠选取单纯形的顶点并 比较各顶点处目标函数值的大小，来寻找下一步的探 索方向的。在用于求解约束问题的复合形法中，复合 形各顶点的选择和替换，不仅要满足目标函数值的下 降，还应当满足所有的约束条件。
基本思想：在可行域中选取K个设计点 （ n+1≤K≤2n）作为初始复合形的顶点。比较各顶点目标 函数值的大小，去掉目标函数值最大的顶点(称最坏点) ，以坏点以外其余各点的中心为映射中心，用坏点的 映射点替换该点，构成新的复合形顶点。
取次好点和好点连线的中点为X(0)。
令：X(4)= X(0)+α(X(0)-X(H))
称X(4)为映射点，记为X(R)，α为映射系数，通常取 α=1.3，可根据实际情况进行缩减。
一般情况下，映射点的函数值比坏点的函数值要 小，即F(X(R))< F(X(H))。若满足可行域，则用X(R)代替 X(H)构成新的复合形。如此反复迭代直到找到最优解。
（3）计算坏点外的其余各顶点的中心点X(0)。
X0
1 K K1j1
X(j),
j
H
（4）计算映射点X(R)
X (R )X (0 )(X (0 )X (H ))
检查X(R)是否在可行域内。若X(R)为非可行点，将映 射系数减半后再按上式改变映射点，直到X(R)进入可行 域内为止。

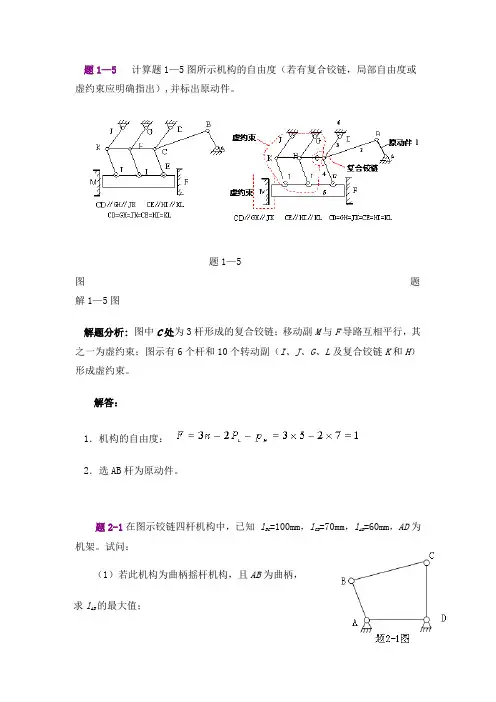
机械设计基础部分例题答案讲解

机械设计基础部分例题答案讲解

题1—5 计算题1—5图所示机构的自由度（若有复合铰链，局部自由度或虚约束应明确指出）,并标出原动件。

题1—5图题解1—5图解题分析: 图中C处为3杆形成的复合铰链；移动副M与F导路互相平行，其之一为虚约束；图示有6个杆和10个转动副（I、J、G、L及复合铰链K和H）形成虚约束。

解答：1．机构的自由度：2．选AB杆为原动件。

题2-1在图示铰链四杆机构中，已知l BC=100mm，l CD=70mm，l AD=60mm，AD为机架。

试问：（1）若此机构为曲柄摇杆机构，且AB为曲柄，求l AB的最大值；（2）若此机构为双曲柄机构，求l AB 最小值； （3）若此机构为双摇杆机构，求l AB 的取值范围。

解题分析：根据铰链四杆机构曲柄存在条件进行计算分析。

在铰链四杆机构中，若满足杆长条件，以最短杆或最短杆相邻的杆为机架，机构则有曲柄，否则无曲柄；若不满足杆长条件，无论取哪个构件为机架，机构均为无曲柄，即为双摇杆机构。

解答：1．因为AD 为机架，AB 为曲柄，故AB 为最短杆，有AD CD BC AB l l l l +≤+，则m m30)1006070(=-+=-+≤BC AD CD AB l l l l故 mm30max =AB l2．因为AD 为机架，AB 及CD 均为曲柄，故AD 杆必为最短杆，有下列两种情况：若BC 为最长杆，则 m m100=<BC AB l l ，且AB CD BC AD l l l l +≤+，则m m90m m )7010060(=-+=-+≥CD BC AD AB l l l l得 m m 100m m 90≤≤AB l若AB 为最长杆，则m m100=>BC AB l l ，且BC CD AB AD l l l l +≤+，故m m110m m )6070100(=-+=-+≤AD CD BC AB l l l l得m m 110m m 100≤≤AB l故m m 90min =AB l3．如果机构尺寸不满足杆长条件，则机构必为双摇杆机构。

机械优化设计数学模型

机械优化设计数学模型

机械优化设计数学模型机械优化设计数学模型是一种用于解决机械设计问题的数学工具。

通过建立数学模型，可以对机械系统的设计进行分析、优化和预测。

在机械设计中，通过数学模型可以量化设计指标，如机械性能、成本、可靠性等，从而帮助设计师作出更好的决策。

最优化方法是机械优化设计中最常用的方法之一、最优化是寻找一个使得目标函数取得最小值或最大值的变量值的过程。

在机械设计中，目标函数通常是与设计指标相关的性能指标，如机械结构的强度、刚度、重量等。

通过最优化方法，可以找到满足设计要求的最佳设计。

约束优化方法是在设计中考虑约束条件的一种方法。

约束条件通常是与设计指标相关的限制条件，如材料的强度、尺寸的限制等。

在机械设计中，约束条件往往是不可或缺的，设计师需要在满足约束条件的前提下，尽量优化设计。

数值模拟方法是通过建立数学模型，应用数值方法进行求解的一种方法。

数值模拟方法不仅可以对机械系统的性能进行估计，还可以通过改变参数进行优化设计。

数值模拟方法在机械设计中的应用非常广泛，如有限元分析、多体动力学分析等。

除了最优化方法、约束优化方法和数值模拟方法，还有其他一些数学方法可以用于机械优化设计。

如统计学方法、灵敏度分析、优化算法等。

这些方法在机械设计中的应用可以根据具体问题进行选择和组合使用。

总之，机械优化设计数学模型是一种重要的工具，可以帮助设计师分析、优化和预测机械设计。

通过建立数学模型，并应用适当的数学方法，可以使机械系统达到更好的性能、成本和可靠性。

机械优化设计数学模型的建立和应用需要设计师具备一定的数学基础和工程经验，同时也需要合理的设计目标和约束条件，才能得到满意的设计结果。

【精选】机械设计基础问答题

【精选】机械设计基础问答题

机械设计基础问答题1.试述机械与机构、零件与构件、运动副与约束的涵义。

①零件是制造的基本单元；②某些零件固联成没有相对运动的刚性组合称为构件，构件是运动的基本单元；③构件与构件之间通过一定的相互接触与制约，构成保持相对运动的可动联接，称为运动副；④当构件用运动副联接以后，它们之间的某些相对运动将不能实现，这种对相对运动的限制称为运动副的约束；⑤能完成有用的机械功或转换机械能的机构组合系统称为机器；⑥机器与机构总称为机械。

2.何谓复合铰链、局部自由度和虚约束？①三个或三个以上的构件在同一轴线上用回转副相联接构成复合铰链；②局部自由度是指不影响机构中输入与输出关系的个别构件的独立运动（凸轮机构中的滚子——提高效率，减少磨损）；③运动副引入的约束中，对机构自由度的影响与其他机构重复，这些重复的约束称为虚约束（机械中常设计带有虚约束，对运动情况虽无影响，但往往能使受力情况得到改善）。

3.机构具有确定运动的条件是什么？若不满足条件，将会出现什么情况？①运动链成为具有确定相对运动的机构的必要条件为：运动链的自由度必须大于零，主动构件数必须等于运功链的自由度；②不满足条件时，当自由度为零时，运动链将成为各构件间没有相对运动的刚性构架，当主动构件数大于自由度时，可能会折断构件，当主动构件数小于自由度时，从动件的运动不确定。

4.试述机件损伤和失效的主要形式以及机件工作准则的涵义。

①机件的主要的损伤及失效形式有：机件产生整体的或工作表面的破裂或塑性变形，弹性变形超过允许的限度，工作表面磨损、胶合和其他破环，靠摩擦力工作的机构产生打滑和松动，超过允许强度的强烈震动，等等；②主要准则：强度——机件抵抗断裂、过大的塑性变形或表面疲劳破坏的能力，刚度——机件受载时抵抗弹性变形的能力，常用产生单位变形所需的外力或外力矩来表示（提高刚度的办法：改进机件结构，增加辅助支撑或肋板以及减小支点的距离，适当增加断面尺寸）耐磨性——磨损过程中抵抗材料脱落的能力，振动稳定性——机器在工作时不能发生超过容许的振动，耐热性。

机械优化设计 第5章 约束优化方法

机械优化设计 第5章 约束优化方法

2. 将(0,1)中的随机数 i 变换到(-1,1)中去;
yi 2i 1
3. 构成随机方向
y1
e
1

y2

n
i 1
yi2
...

yn

i 1,2,...,n
例: 对于三维问题: 1 0.2,2 0.6,3 0.8 变换得: y1 0.6, y2 0.2, y3 0.6
一. 基本思路
搜索方向----采用随机产生的方向 ① 若该方向不适用、可行，则 产生另一方向；
②若该方向适用、可行，则以加 速步长前进；
③若在某处产生的方向足够多， 仍无一适用、可行，则采用收缩 步长；
④若步长小于预先给定的误差限 则终止迭代。
2019/12/12
5
二.随机方向的构成
1.用RND(X)产生n个随机数 i , i 1,2,..., n(0 i 1)
j =1
给定内点 X 0 ,0 , m,
α =α 0, F0=F(X0)
K=0, j=0
0 初始步长； m 在一迭代点处允许产生的方向数； 终止误差限(步长)
产生随机方向
X X 0 S
否
X∈D
是
F=F（X）
否 F<F0 是
X0=X, F0=F
否 j =0
是
K=K+1
2019/12/12
2
二.迭代步骤
X (0) X (3) X (4)
X (1) X (2)
2019/12/12
3
三.存在问题
有时会出现死点, 导致输出“伪最优 点”.
* 为辨别真伪, 要用K-T条件进行检查.

约束优化方法的讲解

根据它们在惩罚函数中的作用，分别称障碍项和惩罚 项。 障碍项的作用是当迭代点在可行域内时，在迭代过程 中将阻止迭代点越出可形域。 惩罚项的作用是当迭代点在非可行域或不满足等式约 束条件时，在迭代过程中将迫使迭代点逼近约束边界或 等式约束曲面。 按照惩罚函数在优化过程中迭代点是否可行，分为： 内点法、外点法及混合法。
2）按经验公式
r0 f x0 1 0 g x j 1 j
m
计算r0 值。这样选取的r0 ，可以是惩罚函数中的障 碍项和原目标函数的值大致相等，不会因障碍项的值 太大则其支配作用，也不会因障碍项的值太小而被忽 略掉。 3.惩罚因子的缩减系数c的选取 在构造序列惩罚函数时，惩罚因子r是一个逐次递 减到0的数列，相邻两次迭代的惩罚因子的关系为：
(k=0,1,2,…)
逐步趋向最优解，直到满足终止准则才停止迭代。
直接解法的原理简单，方法实用，其特点是：
1）由于整个过程在可行域内进行，因此，迭代计算不论 何时终止，都可以获得比初始点好的设计点。 2）若目标函数为凸函数，可行域为凸集，则可获得全域 最优解，否则，可能存在多个局部最优解，当选择的初始 点不同，而搜索到不同的局部最优解。 3）要求可行域有界的非空集。
a) 可行域是凸集；b)可行域是非凸集
间接解法的求解思路：
将约束函数进行特殊的加权处理后，和目标函数结合起来， 构成一个新的目标函数，即将原约束优化问题转化为一个 或一系列的无约束优化问题。
x, 1 , 2 f x 1G hk x g j x 2 H
当迭代点离约束边界越远时，惩罚项愈大，这可看 成是对迭代点不满足约束条件的一种惩罚。
例6-6 用外点法求问题
hk x 0

机械设计中的刚性约束问题探讨

机械设计中的刚性约束问题探讨在机械设计中，刚性约束是一项重要且必不可少的考虑因素。

它不仅影响到机械结构的稳定性和耐用性，还直接关系到产品的使用寿命及其工作效果。

因此，深入研究刚性约束问题对于机械设计的优化和改进具有极其重要的意义。

刚性约束指的是在机械结构设计中，通过各种方式对部件进行约束，使其具有一定的稳定性和刚度。

这样可以减少由于工作载荷、振动等因素引起的变形和松动，确保机械系统的运行稳定性和精度。

然而，在实际设计中，刚性约束问题往往并不容易解决，需要综合考虑各种因素并进行合理的设计。

首先，刚性约束问题在机械系统中通常表现为固定部件的选择和位置布置。

正确选择和布置固定部件对于减少结构变形和振动有着重要的作用。

例如，在汽车发动机的设计中，发动机座的位置和固定方式直接关系到发动机的稳定性和工作效率。

合理的固定方式可以减少发动机运行时的振动和噪音，并延长发动机的使用寿命。

其次，材料的选择和优化也是解决刚性约束问题的关键之一。

材料的强度和刚度与机械结构的稳定性密切相关。

在设计中，需要根据不同部位的受力情况进行合理的材料选择和配比，以确保结构的刚性约束满足设计要求。

例如，在飞机机翼的设计中，航空铝合金材料的使用和优化可以减少机翼变形，提高飞机的操纵稳定性。

此外，合理的约束方式也是解决刚性约束问题的关键。

在机械设计中，各种约束方式如焊接、螺栓连接、键连接等都有其适用的场景和优劣之处。

正确选择和使用适当的约束方式，可以实现刚性约束的效果，并且能够便于拆卸和维护。

例如，在建筑钢结构中，通过焊接和螺栓连接的混合方式进行约束，可以确保结构的稳定性和刚度，并且容易进行拆卸和更换。

另外，刚性约束问题还需要考虑运动部件的设计。

在机械系统中，运动部件的刚性约束对于保持系统的精度和稳定性至关重要。

例如，在机械手臂的设计中，关节的摆动及其约束控制是一个复杂的问题。

合理的关节设计和约束方式，可以减小机械手臂的运动误差，并且提高其工作的精度和稳定性。

机械设计中的约束分析


机械设计
五、机械零件的设计步骤
1）拟订零件的设计简图； 2）确定载荷的大小及位置；
L1 F L2
第二章 约束分析－一般问题
受力分析
3）选择材料； 4）根据失效形式选用承载能力判定条件，
设计或校核零件的主要参数；
强度条件（或刚度） 设计计算 尺寸 设计式
尺寸 校核计算 强度条件（或刚度） 校核式
5）结构设计，绘制零件工作图。
对称循环变应力
稳定循环变应力 脉动循环变应力
非对称循环变应力
机械设计
T
第二章 约束分析－强度问题
对称循环变应力
脉动循环变应力
非对称循环变应力
静应力
机械设计
第二章 约束分析－强度问题
3、变应力的五个特性参数
● 最大应力σmax m a
● 最小应力σmin m a
● 应力幅σa max min （总为正）
循环特征
r min 300 0.652 max 460
应力幅
a
max
min
2
460 300 80MPa 2
属于哪一种类型？
机械设计
问 题： 变应力是否一定由变载荷引起？
变载荷 → 变应力 静载荷 → 静应力 ？或 变应力
第二章 约束分析－强度问题
静载荷 F
n
●
为什么要将应力分成许多类？
2
● 平均应力σm max min
2
已知任意两个参数， 可确定其余参数
● 循环特征 r
min max
m a m a
1 r 1 即：| r | 1
定义规则：
σmax 总为正，且其值不小于σmin 的绝对值； σmax、σmin 在横轴同侧时，r 取“＋”号; 否则，r 取“－”号

02机械设计中的约束分析

第二章 机械设计中的约束分析
§2-1 概述 §2-2 机械设计中的强度问题 机械设计中的摩擦、 §2-3 机械设计中的摩擦、磨损和润滑问题
§1-1 概述
机械设计的基本特征之一是约束性。 机械设计的基本特征之一是约束性。 约束性 经济性约束：降低产品成本， 经济性约束：降低产品成本，将其控制在规定成本目标的 范围之内。 范围之内。 社会性约束：必须能对社会带来效益，而不会对社会造成 社会性约束：必须能对社会带来效益， 不良影响。 不良影响。 技术性约束：能否满足技术性能要求为目标，包括技术 技术性约束：能否满足技术性能要求为目标，包括技术 性能约束、标准化约束、可靠性约束、安全性约束、 性能约束、标准化约束、可靠性约束、安全性约束、维修性 约束等 约束等。
静应力下，对于塑性材料，可取其屈服极限（ 静应力下，对于塑性材料，可取其屈服极限（ σ s ）作为极 限应力， 限应力，即 σ lim = σ s 。 对于脆性材料，可取其强度极限（ 作为极限应力， 对于脆性材料，可取其强度极限（ σ b ）作为极限应力， 即 σ lim = σ b 。
三、变应力作用下的强度问题
注：静应力只在静载荷作用下产生，循环应力可由变载 静应力只在静载荷作用下产生， 荷产生，也可由静载荷产生。 荷产生，也可由静载荷产生。
2. 稳定循环变应力时的强度约束条件
强度：指机械零件工作时抵抗破坏的能力。 强度：指机械零件工作时抵抗破坏的能力。 强度条件有两种表示方法： 强度条件有两种表示方法： 用应力表示： 1） 用应力表示：
三、可靠性约束 可靠性：指产品、部件或零件在规定的使用条件下， 可靠性：指产品、部件或零件在规定的使用条件下， 在预期的使用寿命内能完成规定功能的概率。 在预期的使用寿命内能完成规定功能的概率。 四、安全性约束 （1）零件安全性。 ）零件安全性。 （2）整机安全性。 ）整机安全性。 （3）工作安全性。 ）工作安全性。 （4）环境安全性。 ）环境安全性。 安全性约束：所设计的机器应能满足上述各方面的限制。 安全性约束：所设计的机器应能满足上述各方面的限制。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

min m - a
a
2
max - min
m
max min
非对称循环变应力
2 r min / max
例2-1：设有一零件受变应力作用，已知变应力的平均应力 应力幅为 ＝129Mpa，试求该变应力的循环特征r。
＝189Mpa，
（3）几种稳定循环变应力
（1）不同循环次数N时的疲劳极限：
当应力循环特征r一定时，应力增大，零件失效前 所经历的循环次数N减少；反之，应力减少，循环次数 N增加。当应力减小到某一数值时，零件可经"无数"次 循环而不发生疲劳破坏。图中来自劳曲线可以表示为：＝常数
为材料的疲劳极限，即经"无数"次循环(无限寿命)而不发生疲劳破坏时的极限应力； 为材料条件疲劳极限，即应力循环次数为N(有限寿命)时的极限应力。
）作为
三、变应力作用下的强度问题
1、变应力的种类和特点
（1）静载荷和变载荷均可能产生变应力。在 静载荷F作用下，转动心轴上的a点所受的应 力就是一个对称循环的变应力。
（2）变应力参数（以正应力δ为例，可将τ替 换 δ）
最大应力 最小应力 应力幅 平均应力 循环特征
max a m
2、危险剖面处的计算安全系数[ ；或 式中： 为极限正应力； ]、[ ]不应小于许用安全系数[S]，即： (2-2)
为极限剪切应力； 、 ）作为极
•对于塑性材料：主要失效形式是塑性变形，取其屈服极限（ 限应力，即 ， ； •对于脆性材料：主要失效形式是脆性破坏，取其强度极限（ 极限应力，即 ， 。
、
§2-1 概述
机械设计的主要任务，就是要在由各种约束条件下，寻找设计方案。机械 设计中的约束主要有：经济方面的约束、社会方面的约束和技术方面的约束。
一、技术性能约束 技术性能：包括产品的功能、制造和运行状况在内的一切性能，既指静态 性能，也指动态性能。例如，产品所能传递的功率、效率、使用寿命、强度、 刚度、抗摩擦、磨损性能、振动稳定性、热特性等。 技术性能约束：是指相关的技术性能必须达到规定的要求。 振动会产生额外的动载荷和变应力，尤其是当其频率接近机械系统或零件 的固有频率时，将发生共振现象，这时，振幅将急剧增大，有可能导致零件甚 至整个系统的迅速损坏。 振动性稳定约束：限制机械系统或零件的相关振动参数，如固有频率、振 幅、噪声等在规定的允许范围之内。 热特性：机器工作时的发热性能。可能会导致热应力、热应变，甚至会造 成热损坏。 热特性约束：限制各种相关的热参数(如热应力、热应变、温升等)在规定 范围之内。
三、可靠性约束
可靠性：产品或零部件在规定的使用条件下，在预期的寿命内能完成规定功能的 概率。
四、安全性约束
机器的安全性包括： 零件安全性：指在规定外载荷和规定时间内零件不发生如断裂、过度变形、过度 磨损和不丧失稳定性等等。 整机安全性：指机器保证在规定条件下不出故障，能正常实现总功能的要求。 工作安全性：指对操作人员的保护，保证人身安全和身心健康等等。 环境安全性：指对机器的周围环境和人不造成危害和污染。
T a m 不随时间变
变应力： 随时间而变的应力
不稳定循环： T a m 之一随时间变 随机： 变化无规律
二、静应力作用下的强度问题
强度是指零件在载荷作用下，抵抗断裂、塑性变形及表面失效的能力。强 度约束条件有两种方式： 1、危险剖面处的计算应力（σca、τca）不超过许用应力（[]、[]）， 即： ；或 (2-1)
二、标准化约束
概念的标准化：设计过程中所涉及的名词术语、符号、计量单位等。 实物形态的标准化：对产品、零部件、原材料、设备及能源等的结构形式、尺寸、 性能等，都应按统一的规定选用。 方法的标准化：与生产技术有关的操作方法、测量方法、试验方法等都应按相应 规定实施。 技术文件的标准化：在产品设计过程中，需要形成的各种技术文件等，都应按相 应的规定执行。
则条件疲劳极限
与应力循环次数
的关系为：
式中： 称为寿命系数。因N≥N0时，疲劳极限为 ，此时KN =1；N<N0时 ，此时KN>1；m为与材料性能、应力状态等有关的指数,可由有关手册查取。
（2）不同应力循环特征r时的疲劳极限：
材料相同但应力循环特征r不同时，其极限应力 不同。 最小， 次之，静应 力下的极限应力 或 最大。 、 、 或 均可通过实验取得。非对称循变应 力（-1<r<+1，r ≠1）下的极限应力，可利用简化的极限应力图直接求得。
§2-2 机械设计中的强度问题 一、载荷和应力
1. 载荷
工作载荷： 机器正常工作时所受的实际载荷 (一般难以确定) 名义载荷： 计算载荷： 按原动机功率求得 T 9.55
TC KT
FC KF
P i n ( N m)
(理想状态)
载荷系数 (考虑各种附加载荷)
2. 应力
静应力：不随时间而变的应力 稳定循环：
a 0
r 1
m
max min
2
r0
2 r min / max
0 ( 0 )
-1 ( -1 )
1 ( 1 )
2、稳定循环变应力时的强度条件 在变应力作用下，机械零件的损坏主要是疲劳断裂。疲劳断裂和静应力作 用下的断裂机理不一样：
疲劳断裂是零件表面最大应力处的应力若超过了某一极限值，就会出现疲 劳裂纹，在变应力的反复作用下，裂纹不断扩展，扩展到一定程度后，突然发 生断裂。 这种区别在强度约束条件中，主要表现为极限应力的不同。 静应力作用下：极限应力主要与材料的性能有关。 变应力作用下：其极限应力除了与材料的性能有关外，还与应力的循环特 征r、应力循环次数N、应力集中、零件的表面情况和零件的尺寸大小等有关。 变应力时的极限应力：也称材料的疲劳极限（或持久极限），是当循环特 征为r时，试件受“无数”次应力循环而不发生疲劳断裂的最大应力值。循环次 数不同，疲劳极限不同；循环特征不同，疲劳极限也不同。
非对称循环变应力
脉动循环变应力
对称循环变应力
静应力
max a m
min 0
m a max
2
max - min
m 0 a max - min
r -1
min m - a
a max - min
max min m