用叠加法求挠度与转角

3. 应用叠加原理的若干情况 1 ) 荷载的分解或重组
q m
q
L/2 L/2
L
F
q
q
m L/2 L/2
F
例
q0
EI
A 求图示自由端的挠度。
L2
L2
q0
L
w1
q0
w3
B
w2
L2
L2
w1
q0 L4 8EI
w2
q0 L 24
8EI
q0 L4 128EI
w3
B
L 2
q0 L 23
6EI
L 2
q0 L4 96EI
wA
w1
w2
w3
41q0 L4 384EI
2) 逐段刚化法
依据： 若结构可分为若干部分，且各部分在荷载作用下的 变形不是相互独立的，那么，结构中 A 点的位移是各个部 分在这一荷载作用下的变形在 A 点所引起的位移的叠加。
A EI a
变形刚体
F
F
Fa 2
B
C
a/2
wwww1122
B (F1, F2,, Fn ) B1(F1) B2 (F2 ) Bn(Fn )
yB (F1, F2,, Fn ) yB1(F1) yB2 (F2 ) yBn(Fn )
叠加法的特征： 1、梁在简单载荷作用下挠度、转角应为已知或有变形表可查； 2、叠加法适用于求梁个别截面的挠度或转角值。
分析和讨论
q
在下列不同的支承方 式中，哪一种刚度最高？
q
q
分析和讨论
q
梁由混凝土材料制成，如果横截面从左图改为右图，能 够改善强度吗？能够改善刚度吗？
梁的材料由普通钢改为优质钢，能够改善强度吗？ 梁的材料由普通钢改为优质钢，能够改善刚度吗？

5 / 41
圣才电子书

ql3/6，D＝－ql4/24。
十万种考研考证电子书、题库视频学习平台
故挠曲线方程和转角方程分别为：
w（x）＝qx2（x2＋6l2－4lx）/（24EI），θ（x）＝q（x3－3lx2＋3l2x）/（6EI）
则最大挠度 wmax＝w（x）|x＝l＝ql4/（8EI）；梁端转角 θB＝θ（x）| x＝l＝ql3/（6EI）。
表 5-1-4 叠加原理计算梁的挠度和转角
四、梁的刚度校核·提高梁的刚度的措施（见表 5-1-5）
表 5-1-5 梁的刚度校核及提高措施
3 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台

五、梁内的弯曲应变能 定义：由于梁弯曲变形而存储的能量称为梁内的弯曲应变能。梁在弹性变形过程中，其 弯曲应变能与作用在梁上的外力所作的功相等，常见梁内的弯曲应变能见表 5-1-6。
则最大挠度 wmax＝w（x）|x＝l＝Fl3/3EI；梁端转角 θB＝θ（x）| x＝l＝Fl2/2EI。
图 5-2-1（a）（b） （2）建立如图 5-2-1（b）所示坐标系。 首先列弯矩方程：M（x）＝－q（l－x）2/2，由此可得挠曲线近似方程： EIw″＝－M（x）＝q（l－x）2/2 积分得： EIw′＝－q（l－x）3/6＋C① EIw＝q（l－x）4/24＋Cx＋D② 该梁的边界条件：x＝0，w＝0，x＝0，w'＝0。代入式①、②可确定积分常数：C＝
圣才电子书

十万种考研考证电子书、题库视频学习平台
第 5 章 梁弯曲时的位移
5.1 复习笔记
梁在承受荷载时发生相应的变形，变形后轴线相对原位置将会发生位移、梁的截面将出 现转角，梁内会因变形存储能量。本章首先介绍梁的位移概念，并基于坐标系统建立挠曲线 方程；接着介绍求解梁的位移的方法，根据挠曲线近似微分方程积分和按叠加原理计算；再 介绍梁刚度校核以及提高梁刚度的方法；最后介绍梁弯曲应变能的概念及计算方法。

得： D 0
Pl 2 得： C 16
AC段梁的转角方程和挠曲线方程分别为：
P 2 2 (4 x l ) 16 EI Px y (4 x 2 3 l 2 ) 48 EI
y
P
B
A
x
l 2
C
l 2
x
最大转角和最大挠度分别为：
max A B
ymax y
q 7qa 8k 384 EI
3
q/2
B C
q/2
A B C
顺时针
q/2
例16：图示梁Ｂ处为弹性支座，弹簧刚 度
EI k 求C端挠度fC。 2a 3
q
A
EI k
B
C
2a
a
解：(1)梁不变形，仅弹簧变形引起的C点挠度为 4 3 qa 3qa B处反力=qa fC 1 2 k EI
q
B
x
l
由边界条件： x 0时，y 0
x l时，y 0
得：
ql 3 C , D0 24
梁的转角方程和挠曲线方程分别为：
y
q 2 3 3 (6lx 4 x l ) 24 EI
q
x
A qx y (2lx 2 x 3 l 3 ) 24 EI
ql 3 24 EI
A a a
q
B C
a
qa 12 EI
顺时针
3 3
P=qa
A B
P=qa
m=qɑ²/2
qa qa C B 6 EI 4 EI
4
顺时针
B
q
C
qa 5qa fC B a 8EI 24 EI

平面弯曲内力 134 第8章 由于y ″的正负号与弯矩的正负号相同，如图8-23所示，所以上式右端应取正号，即
()
M x y E I ′′= （8.31）
上式称为挠曲线近似微分方程。

对于静定梁，弯矩可由截面法求得。

于是，求等截面直梁
的变形问题归结为求解一个二阶常微分方程。

图8-23 曲率与弯矩正负号的关系
8.6.3 积分法求梁的挠度和转角
对与等截面直梁，EI 为常量，式（8.31）可改写成
()EIy M x ′′= （8.32） 积分一次可得转角方程
()d EI EIy M x x C θ′==+∫ （8.33） 再积分一次可得挠度方程
()d d EIy M x x x Cx D =++∫∫ （8.34）
上式中的C 、D 为积分常数，可利用梁的边界条件和连续性条件确定。

8.6.4 叠加法求梁的挠度和转角
在弯曲变形很小，且材料服从胡克定律的情况下，挠曲线微分方程是线性的。

又因在很小变形前提下，计算弯矩时，用梁变形前的位置，结果弯矩与载荷的关系也是线性的。

这样梁在几个力共同作用下产生的变形（或支座反力、弯矩）将等于各个力单独作用时产生的变形（或支座反力、弯矩）的代数和。

8.7 梁的刚度计算
在工程实际中，对弯曲构件的刚度要求，就是要求其最大挠度或转角不得超过某一规定的限度，即。

求：（1）横截面上半径为ρA=d/4点处的剪应力和剪应变；（2）单位长度扭转角 。
解：（1） （2）
5.已知薄壁圆轴的外径D=76mm，壁厚 =2.5mm，所承受的转矩M=1.98kN·m，材料的许用应力[τ]=100MPa，剪切弹性模量G=80GPa，许用单位长度扭转角[ ] = 2°/m。试校核此轴的强度和刚度。
13.在板状试件的表面上，沿纵向和横向粘贴两个应变片 和 ，在力F作用下，若测得 ， ，则该试件材料的泊松比为C。A. 3 B.－3 C. 1/3 D.－1/3
14.脆性材料的抗拉能力比抗压能力差，塑性材料的抗拉能力比抗压能力强。
15.静载下塑性材料的强度指标是屈服极限，脆性材料的强度指标是强度极限。
(1)列出弯矩方程。定出如图所示坐标，弯矩方程为M(x)=F(l-x)(2)列挠曲线微分方程并积分EIy’’=F(l-x)
(3)确定积分常数。积分常数可利用边界条件来确定。在悬臂梁中，边界条件是固定端处的转角为零，挠度也为零
(4)列转角方程和挠度方程。可求出梁任一截面的转角和挠度。在自由端B截面处出现最大转角与最大挠度
3.试求图示应力状态的主应力及最大剪应力（应力单位为MPa）。
解： ， 是主应力
MPa
1.一倾斜矩形截面梁AB如图，在其中点C处作用有铅垂力F=25kN，试求梁AB中的最大拉应力和最大压应力。
解：（1）受力分析
力F可分解为F1=Fcos30°和F2=sin30°，梁发生弯曲和压缩的组合变形。最大弯矩发生在C截面 AC段轴力为FN=--sin30°
（3）叠加求C端的挠度yC=y1+y2
1.求图示单元体的主应力。
解：由公式 得 1=8.284 MPa 3= -48.284 MPa 2=0

挠曲轴线 近似微分方程
y M (x) EI
• 叠加原理：当梁为小变形时，梁的挠度和转角均是 载荷的线性函数，可以使用叠加法计算梁的转角和 挠度，即梁在几个载荷同时作用下产生的挠度和转 角等于各个载荷单独作用下梁的挠度和转角的叠加 和，这就是计算梁弯曲变形的叠加原理。
• 叠加原理的步骤： ①分解载荷；②分别计算各载荷 单独作用时梁的变形；③叠加得最后结果。
a
x


5ql 4 384 EI
例6-5 悬臂梁AB上作用有均布载荷q，自由端作 用有集中力F = ql，梁的跨度为l，抗弯刚度为EI，如 图所示。试求截面B的挠度和转角。
解：（1）分解载荷
梁上载荷可分解成均布载 荷 q 与集中力 F 的叠加。
（2）查表得这两钟情况下
截面 B 的挠度和转角
yBq


ql3 2EI


2ql
3
（顺时针）
3EI
例6-6 如图所示，外伸梁在外伸段作用有均布 载荷q，梁的抗弯刚度为EI。求C截面的挠度。
解： 1）简化、分解载荷
2）分别计算 B 截面挠度：
悬臂梁因 B 截面产生转角引
起的挠度 yC1和悬臂梁在均布 载荷作用下产生的挠度 yC2
0.5qa2
qa
+
B


yA3

ql4 8EI

7ql 4 384EI

5Fl3 48EI
41ql4 5Fl3 384EI 48EI
代入数值得：
yA 3.89 103 m 3.89mm（）

ql 4 8EI
+
Bq


ql3 6EI

yC
3 i 1
yCi
5ql4 384EI
ql 4 48EI
ql4 16EI
11ql4 ( ) 384EI
B
3
Bi
i 1
ql3 24EI
ql3 16EI
ql3 3EI
11ql3 ( ) 48EI
目录
材料力学 材料力学
用叠加法求弯曲变形
例4 已知：悬臂梁受力如图示，q、l、
yC
EI均为已知。求C截面的挠度yC和转角C
材料力学
材料力学
用叠加法求弯曲变形
设梁上有n 个载荷同时作用，任意截面上的弯矩 为M(x)，转角为 ，挠度为y，则有：
EI
d2y dx2
EIy''
M(x)
若梁上只有第i个载荷单独作用，截面上弯矩
为 M i ( x) ，转角为 i ，挠度为 yi ，则有：
EIy''i Mi ( x)
材料力学
7-4
解 1）首先，将梁上的载荷变成有表可查 的情形
为了利用梁全长承受均布载荷 的已知结果，先将均布载荷延长至梁 的全长，为了不改变原来载荷作用的 效果，在AB 段还需再加上集度相同、 方向相反的均布载荷。
目录
材料力学 材料力学
用叠加法求弯曲变形
2）再将处理后的梁分解为简单载荷作用
yC
的情形，计算各自C截面的挠度和转角。
等于在各个载荷单独作用时的挠度或转角的代数 和。这就是计算弯曲变形的叠加原理。
材料力学
目录
材料力学 材料力学
用叠加法求弯曲变形
例3 已知简支梁受力如图示，q、l、EI 均为已知。求C 截面的挠度yC ；B截面的 转角B

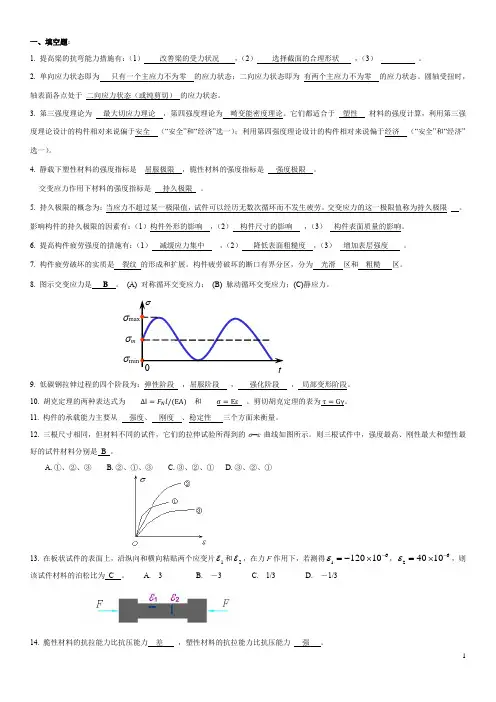
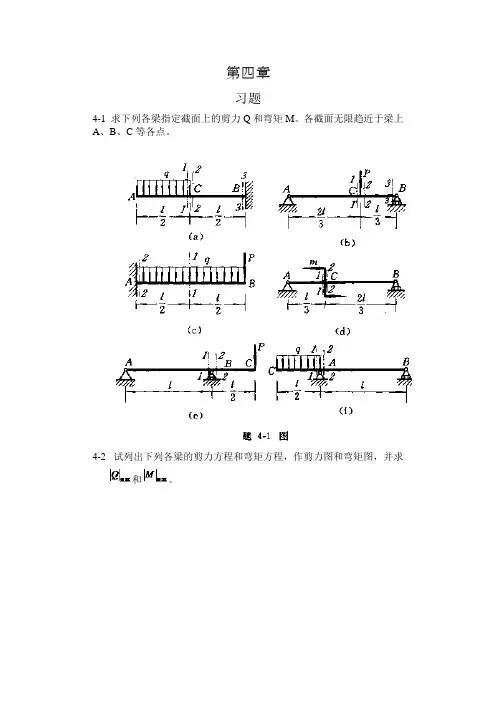
第四章习题4-1 求下列各梁指定截面上的剪力Q和弯矩M。

各截面无限趋近于梁上A、B、C等各点。

4-2 试列出下列各梁的剪力方程和弯矩方程，作剪力图和弯矩图，并求和。

4-3 用叠加法作以下各梁的弯矩图。

并求出。

4-4 用剪力、弯矩和分布载荷集度之间的微分关系校核前面已画的剪力图和弯矩图是否正确。

4-5 不列剪力方程和弯矩方程，作以下各梁的剪力图和弯矩图，并求出和。

4-6 用合适的方法作下列各梁的剪力图和弯矩图。

4-7 试根据载荷、剪力图和弯矩图之间的关系，检查下列各梁的剪力图和弯矩图是否正确，并对错误之处加以改正。

4-8 作下列构件的内力图。

4-9 在梁上行走的小车二轮的轮压均为P ，如图所示。

问小车行至何位置时梁内的弯矩最大？最大弯矩值是多少？设小车的轮距为c，大梁的跨度为。

参考答案4-1 解：题（b）（1）求支反力（见图）由，l-P l=0 =由，（2）剪力按计算剪力的规则（3）弯矩按计算弯矩的规则其它各题的答案：（a）（c）（d）（e）（f）4-2 解：题c(1)剪力和弯矩方程以左端A为原点，任一截面距左端的距离为x（图）\剪力方程:弯矩方程:(2 )剪力图与弯矩图按上述剪力方程和弯矩方程绘剪力图和弯矩图（3）与值由及得=200N =950题（f）（1）求支反力（见图）由，600-1004040=0=由，q4020-60=0=校核：+=2667+1333=4000N=q40=10040 所以支反力计算正确（2）剪力和弯矩方程以左端为原点，任一截面距左端的距离为x，则得剪力方程：弯矩方程（2）剪力图和弯矩图按上述剪力及弯矩方程绘出图及所示的剪力图和弯矩图所示剪力图和弯矩图.图中最大弯矩的截面位置可由，即剪力的条件求得Q（x）=3333-100x=0x=33.3cm（4）及由及得=2667N ，=355其他各题的答案：（a）=ql =（b）（d）（e）（g）（h）（i）（j）4-3 解：题c分别作、q单独作用时的弯矩图（图、），然后将此二图叠加得总的弯矩图。

习 题7-1 用积分法求图示各悬臂梁自由端的挠度和转角，梁的抗弯刚度EI 为常量。

7－1（a ） 0M()M x = ''0EJ M y ∴='0EJ M y x C =+ 201EJ M 2y x Cx D =++ 边界条件: 0x =时 0y = ；'0y = 代入上面方程可求得：C=D=0201M 2EJ y x ∴='01=M EJ y x θ= 01=M EJ B l θ 201=M 2EJ B y l（b ）222()1M()222q l x qx x ql qlx -==-+- 2''21EJ 22qx y ql qlx ∴=-+-3'2211EJ 226qx y ql x qlx C =-+-+422311EJ 4624qx y ql x qlx Cx D =-+-++边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=04223111()EJ 4624qx y ql x qlx ∴=-+-'2231111=(-)EJ 226y ql x qlx qx θ=+-3-1=6EJ B ql θ 4-1=8EJB y ql（c ）()()()()()0303''04'050()1()()286EJ 6EJ 24EJ 120l xq x q lq l x M x q x l x l x l q y l x l q y l x Cl q y l x Cx Dl-=-⎛⎫=--=-- ⎪⎝⎭∴=-=--+=-++ 边界条件：0x = 时 0y = ；'0y = 代入上面方程可求得：4024q l C l -= 50120q l D l =()455000232230120EJ 24EJ 120EJ(10105)120EJq q l q l y l x x l l l q x l l lx x l ∴=---+-=-+- 3024EJ B q l θ=- 4030EJB q l y =-(d)'''223()EJ 1EJ 211EJ 26M x Pa Pxy Pa Pxy Pax Px C y Pax Px Cx D=-=-=-+=-++ 边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=023'232321112611253262B C C B y Pax Px EJy Pax Px EJ Pa Pa Pay y a a EJ EJ EJPa EJθθθ⎛⎫∴=-⎪⎝⎭⎛⎫==-⎪⎝⎭=+=+==(e)()()()21222''1'211231113()02()2223EJ 231EJ ()2231EJ ()46a M x q qax x a q M x a x a x a a y q qaxa y qa x x C a y qa x x C x D =-+≤≤=--≤≤=-+=-++=--+++ 边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=0()()()22118492024EJ 12EJ qax qax y a x a x x a ∴=--=--≤≤''2223'222242232221EJ ((2)4)21EJ (42)2312EJ (2)2312y q a ax x x y q a x ax C x y q a x ax C x D =--+=--++=---+++边界条件：x a = 时 12y y = ；12θθ=代入上面方程可求得：2296a C = 4224qa D =-()()43223421612838464162384q y x ax a x a a a x a EJ-=-+-+≤≤ 43412476B B qa y EJqa EJθ=-=-(f)()()221222''212'231122341115()20225()2225251EJ 22251EJ 26511EJ 4324qa qx M x qax x a qa qa a M x qax x a x a a y q ax x a y q x ax x C a y q x ax x C x D =-+-≤≤⎛⎫=-+--≤≤ ⎪⎝⎭⎛⎫=--+ ⎪⎝⎭⎛⎫=--++ ⎪⎝⎭⎛⎫=--+++ ⎪⎝⎭边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C 1=D 1=0''22'2222223222EJ (2)1EJ (2)21EJ ()6y q a ax y q a x ax C y q a x ax C x D =--=--+=---++ 边界条件：x a = 时 12y y = ； ''''12y y =3296a C =- 4224a D =-437124136B B qa y EJqa EJθ=-=-7-2 用积分法求图示各梁的挠曲线方程，端截面转角θA 和θB ，跨度中点的挠度和最大挠度，梁的抗弯刚度EI 为常量。

EI z1
EI z 2
F
C1
FL32 3EI z2
A
L1
B
L2
C
BF
FL13 3EI z1
BF
FL12 2EI z1
F
B
C
BM
FL2 L12 2EIz1
BM
FL2 L1
EIz1
F
C2 B FB M
A
MFL2
B
C 3B FBM L 2
C
C3C 1C2C3
FL
2 2
3 EI z 2EI zCB源自l2q2DA
l2
q
EI z
C
l2
l2
F 1 qL 4
MB
1 qL2 16
B
q2
A
C
l2
l2
q2
C
A
q2
l2
l2
MB
1 qL2 16
B
5 q L4
C
2 384 EI z
qL 2 16
L 2
16 EI z
qL 4 384 EI z
B
例题 5.9
变截面梁如图示，试用叠加法求自由端的挠度ωc.
F AF BF C2q L0
B
MC FAL12qL2 0
FB 根据对称关系
FB
FA
1qL 2
FC qL
叠加法求挠度
C
FC k
CCqCk
5q 2 L
384 EI z
4
FCy 2L3
48 EI Z
qL 4 24 EI Z
k FC C
24 EI Z L3
例题 5.12 悬臂梁受力如图示.关于梁的挠曲线,由四种答案,请分析判断,哪一个

①
②③ 基础④教学
D
P2
P1 P3 6
11.已知单元体AB、BC面上只作用有剪应力τ，则AC面上的应力
为
C
A、 AC / 2, AC 0
B、 AC / 2, AC 3 / 2
C、AC / 2,
AC 3 / 2
B
D、 AC / 2, AC 0
30
A
C
12.正方形截面杆，横截面边a和杆长l成比例增加，则它的长细 比为 B
C
q
l2 3m
A
B
l1 2m
基础教学
16
05. 已知某危险点的应力状态如图， [σ]=160MPa。试校核强度 （用第三强度理论）
60
50 60
50
（Mpa)
06、房屋建筑中的某一等截面梁简化成均布载荷作用下的双跨梁 （如图所示）。试作梁的剪力图和弯矩图。（12分）
q
A
C
B B 0
l
l
基础教学
d 70mm
e 20mm
P 10.图示受力杆件中，已知P=20kN，M=0.8kNm，直径d=40mm。 试求外表面上A点的主应力。
A P
m P
m
基础教学
19
11、受扭圆轴表面上任一点处与轴线成 方向的线应变 ，材料的E=200Gpa， =0.3， =160Mpa，用第
三强度理论校核其强度。（12分）
T
T
T
(a)圆截面
(b)空心截面
(c)薄壁圆截面
10.偏心压缩实际上就是 压缩 和 弯曲 的组合变形问题。
基础教学
11
11、在压杆稳定性计算中，若将中柔度杆误用了欧拉公式进行计 算，则所得的临界力比实际的临界力值 大 ；而稳定性校核的结 果是偏于危险。

科学技术创新2018.06梁的挠度和转角问题分析王爽焦之森（齐齐哈尔大学建筑与土木工程学院，黑龙江齐齐哈尔161000）对简支梁、外伸梁的变形问题的解析计算方法有很多种，常见的有积分法[1-5]、能量法[1-5]、叠加法[1-5]、奇异函数法[1-5]和共轭梁法[1-5]等，在用积分法求解简支梁、外伸梁的变形问题时须求解多个积分常数，计算繁琐；奇异函数法仍属于积分法，求解过程也须解积分常数；如果仅计算某一截面的位移，能量法较为简单，不过仍须进行积分计算[6]。

本文通过间接叠加法，来介绍简支梁、外伸梁等结构在受载荷作用时挠度及转角问题的简单求解方法，即将简支梁、外伸梁等结构在受载荷作用时挠度及转角问题，转化为有初始转角的悬臂梁受载荷时的变形问题，使简支梁、外伸梁等结构在受载荷作用时挠度及转角问题的求解过程的思维难度得到很大程度的降低，从而问题变得更容易理解。

1原理介绍与例题分析悬臂梁具有一个固定端，当悬臂梁受已经与水平线外荷载作用时，靠近固定端的载面不发生转动，转角为零。

如果有一个悬臂梁，在未荷载时，形成一个小的角度θB ，如图1所示。

图1有初始转角的悬臂梁x 轴为水平方向，梁轴线与x 轴成角θB ，即θB 为初始转角，此梁称为有初始转角的悬臂梁。

在未受荷载时，相对于x 轴，自由端已经有一挠度为θB l 。

根据叠加法，当加一静荷载F 时，自由端的挠度ω=θB l+Fl 33EI 转角为θB +Fl22EI。

应用初始转角悬臂梁概念，只要知道悬臂梁在集中力偶、集中力和均布载荷作用下自由端的挠度和转角公式，就可以通过叠加法，求解简支梁、外伸梁、的变形问题。

跨长l ，刚度EI 的悬臂梁在集中力偶Me ，集中力F ，均布荷载q 作用下，自由端的挠度和转角公式列出如下Mel 22EI ，Mel EI ，Fl 33EI，Fl 23EI ，ql 48EI ，ql 36EI。

下面举几个例子。

例1.如图例2-1所示简支梁端受集中力偶Me 作用，求端截面转角。

弯曲变形基本概念题一、选择题1.梁的受力情况如图所示，该梁变形后的挠曲线如图（）所示(图中挠曲线的虚线部分表示直线，实线部分表示曲线)。

2. 如图所示悬臂梁，若分别采用两种坐标系，则由积分法求得的挠度和转角的正负号为（）。

题2图题1图A．两组结果的正负号完全一致B．两组结果的正负号完全相反C．挠度的正负号相反，转角正负号一致D．挠度正负号一致，转角的正负号相反3.已知挠曲线方程y = q0x(l3 - 3lx2 +2 x3)∕(48EI)，如图所示，则两端点的约束可能为下列约束中的（）。

题3图4. 等截面梁如图所示，若用积分法求解梁的转角、挠度，则以下结论中（）是错误的。

A．该梁应分为AB、BC两段进行积分B．挠度积分表达式中，会出现4个积分常数-26-题4图 题5图 C ．积分常数由边界条件和连续条件来确定D ．边界条件和连续条件表达式为x = 0，y = 0；x = l ，0==右左y y ，0='y 5. 用积分法计算图所示梁的位移，边界条件和连续条件为( )A ．x = 0，y = 0；x = a + l ，y = 0；x = a ，右左y y =，右左y y '=' B ．x = 0，y = 0；x = a + l ，0='y ；x = a ，右左y y =，右左y y '=' C ．x = 0，y = 0；x = a + l ，y = 0，0='y ；x = a ，右左y y =D ．x = 0，y = 0；x = a + l ，y = 0，0='y ；x = a ，右左y y '=' 6. 材料相同的悬臂梁I 、Ⅱ，所受荷载及截面尺寸如图所示。

关于它们的最大挠度有如下结论，正确的是（ ）。

A ． I 梁最大挠度是Ⅱ梁的41倍 B ．I 梁最大挠度是Ⅱ梁的21倍 C ． I 梁最大挠度与Ⅱ梁的相等 D ．I 梁最大挠度是Ⅱ梁的2倍题6图 题7图 7. 如图所示等截面梁，用叠加法求得外伸端C 截面的挠度为（ ）。

（对于土木工程，强度常处于主要地位，刚度常处于从属 地位）
§4.5 梁的刚度计算
三、提高梁的刚度的措施 由梁在简单荷载作用下的变形表和前面的变形计算可看： 由梁在简单荷载作用下的变形表和前面的变形计算可看： 梁的挠度和转角除了与梁的支座和荷载 梁的支座和荷载有关外还取决于 梁的挠度和转角除了与梁的支座和荷载有关外还取决于 下面三个因素： 下面三个因素 材料——梁的位移与材料的弹性模量 E 成反比 成反比； 材料 截面——梁的位移与截面的惯性矩 I z成反比 成反比； 截面—— 跨长——梁的位移与跨长 L 的 n 次幂成正比 次幂成正比。 跨长 次幂， （转角为 L 的 2 次幂，挠度为 L的 3 次幂） 的 次幂） 1、增大梁的抗弯刚度（EIz） 、增大梁的抗弯刚度（ 2、减小跨长或增加支座 、 方法——同提高梁的强度的措施相同 方法 同提高梁的强度的措施相同 3、预加反弯度（预变形与受力时梁的变形方向相反，目的起到 、预加反弯度（预变形与受力时梁的变形方向相反， 一定的抵消作用） 一定的抵消作用）
θ B ( F1 , F2 ,⋅ ⋅ ⋅ ⋅ ⋅⋅, Fn ) = θ B1 ( F1 ) + θ B 2 ( F2 ) + ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ +θ Bn ( Fn )
y B ( F1 , F2 ,⋅ ⋅ ⋅, Fn ) = y B1 ( F1 ) + y B 2 ( F2 ) + ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ + y Bn ( Fn )
D
= 0
θC左 = θC右
§4.4 叠加法计算梁弯曲变形
Me
q
梁上有分布载荷， 梁上有分布载荷，集中力与 集中力偶。 集中力偶。
qx 2 B 弯矩： M = M − Fx − 弯矩： e 2

EI
将其相继积分两次，得
q q d 2 w 3qa x x2 x a 4 2 2 dx 2
2
dw 3qa 2 q 3 q 3 x x xa C dx 8 6 6 qa 3 q 4 q 4 EIw x x x a Cx D 8 24 24 EI
3．确定积分常数
(4)
D1 0 ， C1
由条件（4） 、式（a）与（c） ，得
qa 3 12 EI
C2
由条件（3） 、式（b）与（d） ，得
qa 3 3EI
D2
7qa 4 24 EI
3. 计算截面 C 的挠度与转角 将所得积分常数值代入式（c）与（d） ，得 CB 段的转角与挠度方程分别为
q 3 qa 3 x2 6 EI 3EI 3 q qa 7 qa 4 4 w2 x2 x2 24 EI 3EI 24 EI 将 x2=0 代入上述二式，即得截面 C 的转角与挠度分别为
0
EI
将其相继积分两次，得
d2w M e x Me x a dx 2 2 a
0
dw M e 2 x Me x a C dx 4 a M M 2 EIw e x 3 e x a Cx D 12a 2 EI
3．确定积分常数 梁的位移边界条件为：
(a) (b)
(a) (b)
6
梁的位移边界条件为：
在x 0处， w0 在x 2a处， w0 将条件(c)与(d)分别代入式(b)，得
D 0，C 3qa 3 16
(c) (d)
4．建立挠曲轴方程 将所得 C 与 D 值代入式(b),得挠曲轴的通用方程为
1 qa 3 q 4 q [ x x xa EI 8 24 24 由此得 AC 段与 CB 段的挠曲轴方程分别为 w

叠加法求挠度和转角公式表叠加法是一种用于求解复杂结构挠度和转角的常用方法。

它基于结构受力的叠加原理，将结构的不同组成部分的受力和变形效应分解为简单结构的受力和变形效应，然后通过叠加各部分的受力和变形效应来获得整体结构的受力和变形效应。

以下是常见的几种叠加法求解挠度和转角的公式表。

1.梁的叠加法公式：梁是最简单的结构之一，其挠度和转角的计算比较容易。

常用的梁的叠加法公式有两种：a.常用叠加法公式：若梁由m段相同的子梁组成，每段子梁的长度为l，弹性模量为E，截面惯性矩为I，承受的集中力为P，则整体梁的挠度可以通过以下公式计算：δ=(P*L^3)/(3*E*I)b.斜杆叠加法公式：若梁由m段相同的斜杆组成，每段斜杆的长度为l，弹性模量为E，截面面积为A，承受的集中力为P，则整体梁的挠度可以通过以下公式计算：δ=(P*L)/(E*A)2.杆件叠加法公式：杆件是一种受拉或受压的结构，常见于桥梁和塔等工程中。

常用的杆件叠加法公式有两种：a.拉杆叠加法公式：若拉杆由m段相同的子拉杆组成，每段子拉杆的长度为l，弹性模量为E，横截面积为A，承受的集中力为P，则整体拉杆的伸长量可以通过以下公式计算：Δ=(P*L)/(A*E)b.压杆叠加法公式：若压杆由m段相同的子压杆组成，每段子压杆的长度为l，弹性模量为E，横截面积为A，承受的集中力为P，则整体压杆的压缩量可以通过以下公式计算：Δ=-(P*L)/(A*E)3.板的叠加法公式：板是一种在两个方向上都受力的结构，常见于屋顶和地板等建筑中。

常用的板的叠加法公式有两种：a.弯曲叠加法公式：若板由m段相同的子板组成，每段子板的长度为l，弹性模量为E，截面惯性矩为I，承受的集中载荷为q，则整体板的挠度可以通过以下公式计算：δ=(q*L^4)/(185*E*I)b.剪切叠加法公式：若板由m段相同的子板组成，每段子板的长度为l，弹性模量为E，截面形状系数为k，承受的集中剪力为V，则整体板的转角可以通过以下公式计算：θ=(V*L^3)/(3*E*I*k)需要注意的是，上述公式都是基于一些理想化假设得出的近似解，实际工程中可能还需要考虑其他因素，如材料的非线性特性、结构的非均匀性等。

习惯上将二者统称为叠加法。
12
机电李禄昌
例题5： 用叠加法求图示梁Ｃ端的转角和挠度。
解：⑴、假想将外伸梁分成两部
分，AB段为简支梁；BC段为悬臂 梁。截面B处有剪力P2和弯矩m 。 ⑵、分析AB段的变形： 截面B处有剪力P2和弯矩m ： P2= q a ，m = qa2/2 。 在m作用下，B处的转角：
y
y
n

x

E
( , )
2
A( x , x )
x
B( y , y )
x
c
22

机电李禄昌
三、应力圆的应用： 1、利用应力圆，可以方便求出任意斜截面上的σ
α
、τ
α：
y
y
y
n

x

x
( , )
2
A( x , x )
x
c
B( y , y )
18
机电李禄昌
极值正应力σmax、σmin
（主应力）
2
max x y x y 2 xy min 2 2
极值正应力所在平面的方位角α0
（主平面方向）
tg 20
2 xy
x y
可以求出两个角度值：α0、 α0+π/2，其中一个是最大正应力 σmax 所在平面，另一个是最小正应力σmin 所在平面。
2.叠加原理的限制 ：载荷与它所引起的变形成线性关系。 因此要求（1）材料是线弹性材料，服从胡克定律；
（2）弯曲变形很小。
11
机电李禄昌
叠加法求弯曲变形
载荷叠加法:分解载荷,适用于求解简支梁或者悬 臂梁同时受到几种载荷共同作用下的变形