第七章-梁的位移-转角、挠度
- 格式:ppt
- 大小:1.88 MB
- 文档页数:42
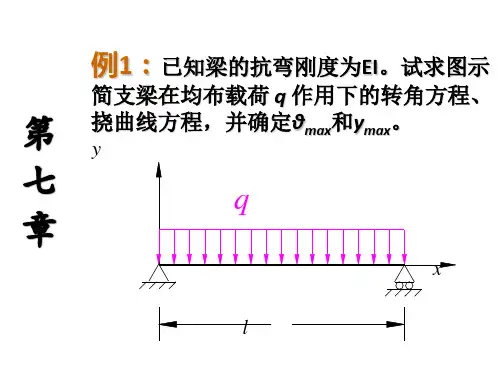
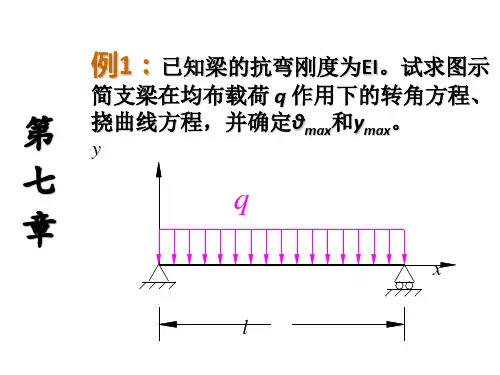

习 题7-1 用积分法求图示各悬臂梁自由端的挠度和转角,梁的抗弯刚度EI 为常量。
7-1(a ) 0M()M x = ''0EJ M y ∴='0EJ M y x C =+ 201EJ M 2y x Cx D =++ 边界条件: 0x =时 0y = ;'0y = 代入上面方程可求得:C=D=0201M 2EJ y x ∴='01=M EJ y x θ= 01=M EJ B l θ 201=M 2EJ B y l(b )222()1M()222q l x qx x ql qlx -==-+- 2''21EJ 22qx y ql qlx ∴=-+-3'2211EJ 226qx y ql x qlx C =-+-+422311EJ 4624qx y ql x qlx Cx D =-+-++边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=04223111()EJ 4624qx y ql x qlx ∴=-+-'2231111=(-)EJ 226y ql x qlx qx θ=+-3-1=6EJ B ql θ 4-1=8EJB y ql(c )()()()()()0303''04'050()1()()286EJ 6EJ 24EJ 120l xq x q lq l x M x q x l x l x l q y l x l q y l x Cl q y l x Cx Dl-=-⎛⎫=--=-- ⎪⎝⎭∴=-=--+=-++边界条件:0x = 时 0y = ;'0y = 代入上面方程可求得:4024q l C l -= 50120q l D l=()455000232230120EJ 24EJ 120EJ(10105)120EJq q l q l y l x x l l l q x l l lx x l ∴=---+-=-+- 3024EJ B q l θ=- 4030EJB q l y =-(d)'''223()EJ 1EJ 211EJ 26M x Pa Pxy Pa Pxy Pax Px C y Pax Px Cx D=-=-=-+=-++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=023'232321112611253262B C C B y Pax Px EJy Pax Px EJ Pa Pa Pay y a a EJ EJ EJPa EJθθθ⎛⎫∴=- ⎪⎝⎭⎛⎫==-⎪⎝⎭=+=+==(e)()()()21222''1'211231113()02()2223EJ 231EJ ()2231EJ ()46a M x q qax x a q M x a x a x a a y q qaxa y qa x x C a y qa x x C x D =-+≤≤=--≤≤=-+=-++=--+++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=0()()()22118492024EJ 12EJ qax qax y a x a x x a ∴=--=--≤≤''2223'222242232221EJ ((2)4)21EJ (42)2312EJ (2)2312y q a ax x x y q a x ax C x y q a x ax C x D =--+=--++=---+++边界条件:x a = 时 12y y = ;12θθ=代入上面方程可求得:2296a C = 4224qa D =-()()43223421612838464162384q y x ax a x a a a x a EJ-=-+-+≤≤43412476B B qa y EJqa EJθ=-=-(f)()()221222''212'231122341115()20225()2225251EJ 22251EJ 26511EJ 4324qa qx M x qax x a qa qa a M x qax x a x a a y q ax x a y q x ax x C a y q x ax x C x D =-+-≤≤⎛⎫=-+--≤≤ ⎪⎝⎭⎛⎫=--+ ⎪⎝⎭⎛⎫=--++ ⎪⎝⎭⎛⎫=--+++ ⎪⎝⎭边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C 1=D 1=0''22'2222223222EJ (2)1EJ (2)21EJ ()6y q a ax y q a x ax C y q a x ax C x D =--=--+=---++ 边界条件:x a = 时 12y y = ; ''''12y y =3296a C =- 4224a D =-437124136B B qa y EJqa EJθ=-=-7-2 用积分法求图示各梁的挠曲线方程,端截面转角θA 和θB ,跨度中点的挠度和最大挠度,梁的抗弯刚度EI 为常量。


梁的挠度和转角问题分析梁的挠度和转角问题分析【引言】梁是工程中常见的结构构件之一,广泛应用于桥梁、楼板、悬挑等结构中。
在梁的工作过程中,挠度和转角是重要的力学参数,在设计和分析中起着重要作用。
本文将从理论和实际应用两个方面,对梁的挠度和转角问题进行分析。
【理论分析】1. 梁的基本原理梁是一种受力的构件,根据受力原理,梁可以被看作是许多个点质量组成的杆件。
在梁受到外力作用时,会产生内力和应变,从而引起梁的变形。
梁的挠度和转角是反映梁变形程度的重要参数。
2. 梁的挠度计算方法梁的挠度通常通过数学方程的求解来计算。
根据不同的边界条件和受力情况,可以采用不同的方法进行计算,如弯曲理论、拉伸理论、弯剪耦合理论等。
其中,弯曲理论是工程设计中常用的方法,利用欧拉-伯努力学说和简化假设,将梁的弯曲变形转化为微分方程求解问题。
3. 梁的转角计算方法梁的转角是指梁在受到外力或自重荷载作用时所产生的旋转变形。
在计算转角时,通常使用梁的弯矩与切线刚度的关系,通过积分计算得到。
转角的计算对于解决梁的位移和变形问题具有重要意义。
【实际应用】1. 桥梁工程中的挠度问题在桥梁工程中,挠度是重要的考虑因素之一。
过大的挠度会影响桥梁的使用寿命和安全性。
因此,在桥梁设计中需要进行挠度计算和控制。
通过实际工程实例,我们可以分析不同型式桥梁的挠度问题,如悬索桥、拱桥和梁桥等。
2. 楼板设计中的转角问题楼板作为建筑结构中的重要组成部分,其转角问题也需要得到充分考虑。
在楼板设计中,不同荷载条件下的转角计算是确保结构安全和满足使用要求的关键。
本文将分析楼板转角对结构整体性能和使用功能的影响,并提供相应的设计建议。
【结论】梁的挠度和转角问题是工程设计和分析中不可忽视的重要内容。
通过理论分析和实际应用,我们可以更好地理解梁的变形行为,并对梁的设计和优化提供参考,以确保结构的安全性和可靠性。
工程实践中的案例表明,挠度和转角分析在工程中起到了重要的引导作用,对于提高结构的设计水平和工程质量具有重要意义综上所述,梁的转角计算对于解决梁的位移和变形问题具有重要意义。


梁的弯曲第七章答案思考题1、什么是梁的纯弯曲?什么是梁的横力弯曲?当梁的横截面上仅有弯矩而无剪力,即仅有正应力而无切应力的情况,称为纯弯曲。
横截面上同时存在弯矩和剪力,即既有正应力又有切应力的情况,称为横力弯曲或剪切弯曲。
2、什么是纵向对称截面?什么是中性层和中性轴?中性轴的位置如何确定?梁的横截面一般至少有一个对称轴,因而由各横截面的对称轴组成了梁的一个纵向对称面。
梁弯曲时部分纤维伸长,部分纤维缩短,由伸长区到缩短区,其间必存在一长度不变的过渡层,称为中性层,中性层与横截面的交线称为中性轴。
3、画剪力图和弯矩图的一般步骤是什么?弯曲变形时,如何确定梁的危险截面?a.利用平衡方程求出梁上的全部约束反力;b.判断梁上各段Q、M图的形状;c.确定关键点的剪力和弯矩值,并作图。
d.在图中找到最大剪力和最大弯矩的值,从而确定危险截面。
等截面梁弯曲时,最大弯矩所在的截面为危险截面。
4、弯曲变形时,梁的正应力在横截面上如何分布?如何确定梁横截面的危险点?梁弯曲时,横截面上任一点处的正应力与该截面上的弯矩成正比,与惯性矩成反比,与该点到中心轴的距离y 成正比。
y 值相同的点,正应力相等;中性轴上各点的正应力为零。
在中性轴的上、下两侧,一侧受拉,一侧受压。
距中性轴越远,正应力越大。
梁横截面的危险点是到中心轴的距离最远的点。
5、什么是挠曲线?什么挠度?什么是转角?它们之间有何关系?直梁发生弯曲变形时,除个别受约束处以外,梁内各点都要移动,即都有线位移。
由于各个横截面形心的线位移不同,以致原为直线的形心轴变为平滑曲线,这个曲线称为挠曲线。
受弯曲变形的简支梁,在C 截面,梁横截面的形心变形后移到C ’截面,则梁横截面的形心沿y 轴方向的线位移称为该截面的挠度。
梁的横截面对其原有位置的角位移,称为该截面的转角。
关系:)('tan x f dxdy ==≈θθ。
习题7-1最大剪力值为7qa/4 。
最大弯矩值为7-2 (1)图略(2)MPa 9200max =σ。



《梁的挠度和转角问题分析》篇一一、引言在工程结构中,梁作为基本的结构构件,其承载能力和稳定性对于整个结构的性能至关重要。
梁在受到外部载荷作用时,会产生挠度和转角,这些变形对结构的整体性能和安全性有着重要影响。
因此,对梁的挠度和转角问题进行分析,对于保障工程结构的安全性和稳定性具有重要意义。
本文将针对梁的挠度和转角问题进行分析,探讨其产生原因、影响因素及解决方法。
二、梁的挠度和转角产生原因梁的挠度和转角是由于外部载荷作用在梁上,导致梁发生变形。
其中,挠度是指梁在受到外部载荷作用时,其垂直于轴线的位移;转角则是指梁在受到外部载荷作用时,其轴线方向的转动角度。
这些变形会影响梁的承载能力和稳定性,严重时可能导致结构失效。
三、影响梁的挠度和转角的因素1. 载荷大小:外部载荷越大,梁的挠度和转角越大。
2. 梁的跨度:梁的跨度越大,其抵抗变形的能力越弱,挠度和转角越大。
3. 梁的材料性质:梁的材料弹性模量、截面惯性矩等材料性质对梁的抗变形能力有重要影响。
4. 支座条件:支座的刚度和位置对梁的挠度和转角也有影响。
四、梁的挠度和转角问题分析针对梁的挠度和转角问题,需要进行以下分析:1. 理论分析:通过理论计算,分析梁在受到外部载荷作用时的挠度和转角,了解其变形规律和影响因素。
2. 实验研究:通过实验测试,验证理论分析的准确性,并了解实际工程中梁的挠度和转角情况。
3. 数值模拟:利用有限元等方法,对梁进行数值模拟分析,了解其在不同载荷和支座条件下的变形情况。
4. 问题诊断:针对实际工程中出现的梁的挠度和转角问题,进行诊断和分析,找出问题的原因和影响因素。
五、解决方法针对梁的挠度和转角问题,可以采取以下解决方法:1. 优化设计:通过优化梁的截面形状、跨度、支座条件等设计参数,减小其挠度和转角。
2. 选择合适的材料:选择具有较高弹性模量和较好力学性能的材料,提高梁的抗变形能力。
3. 加强支撑:在需要的地方增加支撑,提高梁的稳定性,减小其挠度和转角。
