各种梁的受力及挠度、转角计算

悬臂梁弯曲刚度公式
挠度计算公式：Ymax=5ql^4/(384EI)(长l的简支梁在均布荷载q作用下，EI是梁的弯曲刚度）
挠度：弯曲变形时横截面形心沿与轴线垂直方向的线位移称为挠度，用γ表示。

转角：弯曲变形时横截面相对其原来的位置转过的角度称为转角，用θ表示。

挠度与荷载大小、构件截面尺寸以及构件的材料物理性能有关。

挠曲线方程：挠度和转角的值都是随截面位置而变的。

在讨论弯曲变形问题时，通常选取坐标轴x向右为正，坐标轴y向下为正。

选定坐标轴之后，梁各横截面处的挠度γ将是横截面位置坐标x的函数，其表达式称为梁的挠曲线方程，即γ=f(x)。

梁的抗弯刚度计算公式：ymax=(8Pl^3)/(Ebh^2)。

抗弯刚度是指物体抵抗其弯曲变形的能力。

早期用于纺织。

抗弯刚度大的织物，悬垂性较差；纱支粗，重量大的织物，悬垂性亦较差，影响因素很多，有纤维的弯曲性能、纱线的结构、还有织物的组织特性及后整理等。

悬臂梁挠度计算公式为：Ymax=8pl^3/(384ED)=1pl^3/(48ED)，在这个公式式中每个部分都有所指，所以要弄清楚之后才可使用，首先Ymax梁跨中的最大挠度(mm)，而p要为各个集中荷载标准值之和(kn)，之后E主要是指钢的弹性模昰不同情况有不一样的标准，比如对于工程用结构钢，E就
2100000N/mm^2，最后是钢的截面惯矩可在型钢表中查出(mm^4)，这就是整体的公式，可以完整采用。

A
x y

cB
F
x
挠曲方程
W =y= f(x)
yw

（a）
c′
dy
dx B′
tg = dy/dx = y ′
∵挠曲线是一条极其平坦的弹性曲线
∴ 很小 ≈ tg=dy/dx= f ′(x)
转角方程 =y ′ = f ′(x)
(b)
4.符号规定
挠度w 向下为正 转角 由横截面到斜截面顺时针为正
EXAMPLE 5-3 图示一弯曲刚度为EI的简支梁，
在D点处确定其最大挠度和最
大转角。
a
Fb
A
c
B
L
最大挠度和最大转角
A
1
x0

Fab(l b) 6lEI
B
2
xl

Fab(l a) 6lEI
梁上无拐点 wmax w1/ 2
2）一次积分获转角方程
（5-2b）
EIzy′= - ∫M(x) dx+c 3）二次积分获挠度方程
（5-3a） （5-3b）
EIzy= - ∫[∫M(x) dx] dx +Cx+D
C、D为方程的积分常数
4 由边界条件(boundary condition) 确定 积分常数。
4、由边界条件确定积分常数
x3

l2
b2
x]
§5-3 按叠加原理计算 梁的挠度及转角
§5-3 Approximately Differential Equation for Deflection Curve of Beam and It’s Integration
1. 叠加原理的适用范围 2.叠加原理

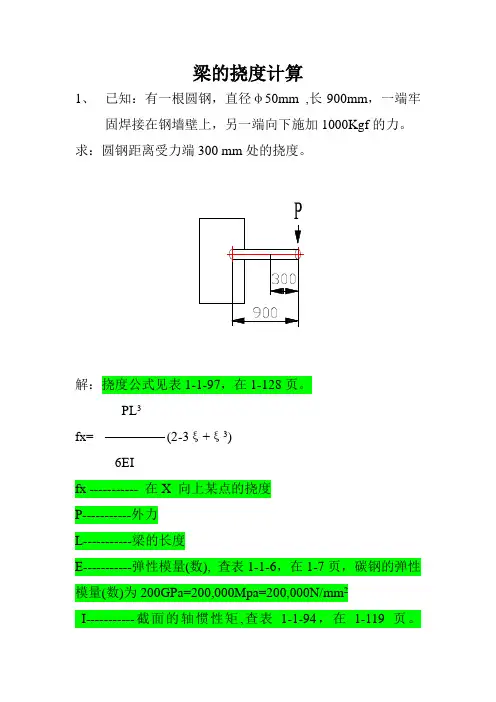
梁的挠度计算1、已知：有一根圆钢，直径φ50mm ,长900mm，一端牢固焊接在钢墙壁上，另一端向下施加1000Kgf的力。

求：圆钢距离受力端300 mm处的挠度。

解：挠度公式见表1-1-97，在1-128页。

PL3fx= (2-3ξ+ξ3)6EIfx ----------- 在X 向上某点的挠度P-----------外力L-----------梁的长度E-----------弹性模量(数), 查表1-1-6，在1-7页，碳钢的弹性模量(数)为200GPa=200,000Mpa=200,000N/mm2I-----------截面的轴惯性矩,查表1-1-94，在1-119页。

I=0.0491d4=0.0491×504=306875ξ----------要求挠度的点到受力端的距离/梁的长度,ξ=300/900=0.3339.8×1000×9003fx= (2-3×0.333+0.3333) 6×200000×306875fx=20.14mm答：圆钢距离受力端300 mm处的挠度为20.14mm。

2、已知：有一根圆钢，直径φ50mm ,长1200mm，两端放在在两个三角形钢轨上，两个三角形钢轨距离1000 mm，在钢轨中间向下对圆钢施加1000Kgf的力。

求：圆钢加力处的挠度。

解：挠度公式见表1-1-97，在1-130页。

PL3fc=48EIfc ----------- 在中间点的挠度P-----------外力L-----------梁两端支撑点的距离E-----------弹性模量(数),查表1-1-6，在1-7页，碳钢的弹性模量(数)为200GPa=200,000Mpa=200,000N/mm2I-----------截面的轴惯性矩,查表1-1-94，在1-119页。

I=0.0491d4=0.0491×504=3068759.8×1000×10003fx=48×200000×306875fx=3.33mm答：圆钢加力处的挠度为3.33mm。

qa 4 f 2C 8EI z qa3 2C 6EI z
f2B qa 4 qa3 ( L a) 8EI z 6 EI z
c L (1) L a
f2c
B
B
2c
B B
A
q
c
(2)
由叠加原理

f B f1B f 2 B
qL4 qa 4 qa3 ( L a) 8EI z 8EI z 6EI z
材料——梁的位移与材料的弹性模量 E 成反比； 截面——梁的位移与截面的惯性矩 I 成反比； 跨长——梁的位移与跨长 L 的 n 次幂成正比。 （转角为 L 的 2 次幂，挠度为 L的 3 次幂） 1、增大梁的抗弯刚度（EI） 2、调整跨长和改变结构 方法——同提高梁的强度的措施相同
3、预加反弯度（预变形与受力时梁的变形方向相反，目的起到 一定的抵消作用）
w max L w L

max

、设计截面尺寸： (对于土建工程，强度常处于主要地位，刚度
、设计载荷：
常处于从属地位。特殊构件例外）
三、提高梁的刚度的措施 由梁在简单荷载作用下的变形表和前面的变形计算可看：
梁的挠度和转角除了与梁的支座和荷载有关外还取决于
下面三个因素：
式中 ，x 为梁变形前轴线上任一点的横坐标 ，y为该点的挠度。
B
A
C
x
挠曲线
C'

B
转角
y挠度
y
4、挠度和转角的符号约定
挠度：向下为正，向上为负。
转角：自x 转至切线方向，顺时针转为正，逆时针转为负。
A
C
B
x
挠曲线
C'

Fy RA RB F 0 RA 0.5F mA RB l F 1.5l 0 RB 1.5F
2．内力分析：分区段列出梁的弯矩方程：
1 M Fx1 1 2 3 M 2 F ( l x2 ) 2
、设计载荷：
常处于从属地位。特殊构件例外）
[例8] 图示木梁的右端由钢拉杆支承。已知梁的横截面为边长 a=200mm的正方形，均布载荷集度 q 40 kN/m ，弹性模量 E1=10GPa ， 钢 拉 杆 的 横 截 面 面 积 A=250mm2 ， 弹 性 模 量 E2=210GPa，试求拉杆的伸长量及梁跨中点D处沿铅垂方向的位 移。
P( x a ) M ( x) 0 (0 x a) (a x L)
a L f
P x
写出微分方程并积分
P( a x) EIf 0
(0 x a) ( a x L)
1 3 P(a x) C1 x C2 EIf 6 D1 x D2
梁的刚度校核

max

1 1 f (对土建工程 : ( ~ )) 250 1000 L
其中[]称为许用转角；[f/L]称为许用挠跨比。通常依此条 件进行如下三种刚度计算： 、校核刚度：
f
max
L
f L

max

、设计截面尺寸： (对于土建工程，强度常处于主要地位，刚度
(顺时针)
转角为： C C1 C 2
Fl 2 Fl 2 9 Fl 2 8EI EI 8EI
说明：对于图(a)：BC段无内力，因而BC段不变形，BC段为
直线 。
[例6] 按叠加原理求C点挠度。 解：载荷无限分解如图

悬臂梁挠度计算公式
根据应变-位移公式，我们可以得到悬臂梁在受力下的挠度计算公式。

公式为：
δ=(P*L^3)/(3*E*I)
其中，δ代表悬臂梁的挠度，P代表悬臂梁上的受力，L代表悬臂梁
的长度，E代表悬臂梁的弹性模量，I代表悬臂梁的截面转动惯量。

这个公式是基于悬臂梁的假设条件以及材料的线性弹性特性。

假设悬
臂梁所受的力是集中作用于梁的一端，且力的作用方向与梁的轴线一致。

此外，该公式还假设悬臂梁的材料是线性弹性材料，即满足胡克定律。

在工程实际中，悬臂梁的材料通常是钢、混凝土、木材等，这些材料
的弹性模量和截面转动惯量可以通过实验或材料手册得到。

根据这些参数，可以进行悬臂梁挠度的计算。

需要注意的是，悬臂梁的挠度公式是在假设条件下得出的近似解，并
且只适用于线性弹性材料、小挠度和小变形的情况。

对于非线性弹性材料、大变形或大挠度的情况，需要采用更加复杂的方法来进行挠度的计算。

总之，悬臂梁的挠度计算公式是用来计算悬臂梁在受力作用下的挠度
的公式。

该公式是基于应变-位移公式和力学平衡条件推导得到的，适用
于线性弹性材料、小挠度和小变形的情况。

在实际工程中，需要根据具体
的材料参数和假设条件来进行准确的挠度计算。

一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
C'
y
1'
1
Байду номын сангаас
y f ( x)
——挠曲线方程
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x

y
1'
y
C'
1
在小变形下： 即：
dy y tan dx
——转角方程
任一横截面的转角 = 挠曲线在该截面形心处切线的斜率
2
9 ql 2 128
M max
1 2 M A ql 8
例 14 试作图示超静定梁的剪力图和弯矩图。
q
5.讨论 设MA为多余约束力 列变形几何方程
A Aq AM 0
A
A l
B 原结构
q MA A B 静定基
查表
Aq
ql M Al ， AM A 24 EI 3 EI
5Fl 3 Fl 2 Fl 3 l 6 EI 3 EI 2 EI
F A l C l
Me B
yBM
A F A C B
e
BM
B
e
Me
BF
yBF
3. Me和F共同作用时
2 M e l Fl 2 B BM e BF EI 2 EI 2 M e l 2 5Fl 3 y B y BM e y BF EI 6 EI
2.确定积分常数
FBy=
l
Me l
由 y x 0 0, D 0

C
q
B
（ d）
C
wc1 (q)
c1 (q)
2 AB变形，BC不变形（刚化）。
ml c 2 (q ) B (q ) 3EI 2 1 3 qa 2 a qa 2 3 EI 3 EI 4 qa wc 2 (q) B (q) a 3 EI
A
qa2/2
B
（e）
AD : Fb( l 2 b 2 ) Fbx2 1 w1 6 EI 2 EIl
Fb( l 2 b 2 ) Fb 3 w1 x x 6 EIl 6 EIl
y
l
HOHAI UNIVERSITY
DB :
Fb( l 2 b 2 ) Fb 2 F 2 w x ( x a ) 2 2 6 EIl 2 EIl 2 EI
M x w EI z
—— 挠曲线近似微分方程
HOHAI UNIVERSITY
§4-9 用积分法计算梁的挠度与转角
对于等截面梁，EI = 常数。
E I w "= - M (x)
EIw EI M ( x )dx C

EIw [ M ( x)dx ]dx Cx D
θ p
A
y
C w C p θ
B x
1、挠度: 梁的截面形心在垂直于轴线方向的线位 移w。 w= w(x)——挠曲线方程(挠度方程)。向下为正.
2、转角：梁的截面绕中性轴转过的角度θ。
小变形时，θ≈tanθ=dw (x)/dx=w'(x)——转角方
程。顺时针为正。
HOHAI UNIVERSITY
§4-8 梁的挠曲线近似微分方程
B
x

&
$# ,
即得 +’()
!’
"
#$ + ,-%
（ ) $ $）*
#
*’() "
#$ %
} $ ,-$（ ( & )）,
[ ( ) %# &
)$
$ #
#
( ) $ #
$&
*
[ )$
$ #%
) $ $! (!+ " +&,#-$（% ) $ $）（ % & (）*
] &
$# ,
(
$ #
$ &) ]
[ ( ) %# &
’" ! ’& ! &
# +
!$
’! !
# +
!$
（) (）!
& !$% (+ *+
[ %(
) ( (
$
" &(
-" $"
’! ! ’)’"0+ -" $"
在 (’ ! ’)((1 $
（) (）!
[ ( ) & -" $(
#"’ *+
( $
&"
("
$
$
(
( $
)*]
在 ( ! ’)((1 $ 处：
)-./
!
& -" $( (#0 *+
!"
!
-" $% #"’ *+
!" ! !& !

悬臂梁的挠度计算公式均布荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 5ql^4/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).q 为均布线荷载标准值(kn/m).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨中一个集中荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 8pl^3/(384EI)=1pl^3/(48EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨间等间距布置两个相等的集中荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 6.81pl^3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨间等间距布置三个相等的集中荷载下的最大挠度,其计算公式: Ymax = 6.33pl^3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).悬臂梁受均布荷载或自由端受集中荷载作用时，自由端最大挠度分别为的,其计算公式:Ymax =1ql^4/(8EI). ;Ymax =1pl^3/(3EI).q 为均布线荷载标准值(kn/m). ;p 为各个集中荷载标准值之和(kn).挠度计算公式：Ymax=5ql^4/(384EI)(长l的简支梁在均布荷载q作用下，EI是梁的弯曲刚度）挠度与荷载大小、构件截面尺寸以及构件的材料物理性能有关。

悬臂梁的挠度计算公式悬臂梁的挠度计算公式均布荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 5ql^4/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).q 为均布线荷载标准值(kn/m).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨中一个集中荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 8pl^3/(384EI)=1pl^3/(48EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨间等间距布置两个相等的集中荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 6.81pl^3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨间等间距布置三个相等的集中荷载下的最大挠度,其计算公式: Ymax = 6.33pl^3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).悬臂梁受均布荷载或自由端受集中荷载作用时，自由端最大挠度分别为的,其计算公式:Ymax =1ql^4/(8EI). ;Ymax =1pl^3/(3EI).q 为均布线荷载标准值(kn/m). ;p 为各个集中荷载标准值之和(kn).挠度计算公式：Ymax=5ql^4/(384EI)(长l的简支梁在均布荷载q 作用下，EI是梁的弯曲刚度）挠度与荷载大小、构件截面尺寸以及构件的材料物理性能有关。

C2 0
C1
ql
24
梁的转角方程和挠曲线方程分别为
'
qx 24 EI q 24 EI (l 2lx x )
3 2 3
(l 6lx 4 x )
3 2 3
RA
A
x
q
A
l 2
RB
B
在 x0 和 xl 处 转角的绝对值相等， 且都是最大值
x
CθB
y
3
l
θ
max
qc
5qL
4
C
z
l 2
384 EI z
转角（） ：横截面对其原来位置的角位移 , 称为该截面的
转角。
转角
A C B x
ω 挠度
C' y B'
挠曲线 ：梁变形后的轴线称为挠曲线 。
挠曲线方程为
f ( x)
式中 ，x 为梁变形前轴线上任一点的横坐标 ，ω为该点的挠度。
挠度与转角的关系： tg ' f '( x)
C
y
连续条件
x
L 2
B1 B 2
B1 B 2
例题 5.6
用积分法求图示梁挠曲线方程时,试问下列梁的挠曲线
近似微分方程应分几段;将分别出现几个积分常数,并写出其确 定积分常数的边界条件。 挠曲线方程应分两段AB,BC.
F
EI
z1
共有四个积分常数
x
EI
z2
边界条件
A
L 2
B
RA RB ql 2
A
x
q
B
l
x
y 例题 5 .2图
此梁的弯矩方程及挠曲线微分方程分别为

混凝土梁挠度的计算方法一、介绍混凝土梁是一种常用的结构构件，它广泛应用于建筑、桥梁、隧道等工程领域。

在使用过程中，混凝土梁的挠度是一项非常重要的性能指标，它直接关系到梁的承载能力和使用寿命。

因此，正确计算混凝土梁的挠度是非常必要的。

本文将介绍混凝土梁挠度的计算方法，包括混凝土梁的基本知识、挠度计算的基本原理、计算方法以及实例分析等。

二、混凝土梁的基本知识1. 混凝土梁的构造混凝土梁是由混凝土和钢筋组成的复合材料，通常由上下两层钢筋和中间的混凝土组成。

其中，上下两层钢筋被称为受拉钢筋，它们的主要作用是抵抗梁的受拉应力。

中间的混凝土则承受梁的压力和剪力。

2. 混凝土梁的受力混凝土梁在使用过程中，会受到多种力的作用，包括自重、荷载、温度变化、湿度变化等。

其中，荷载是混凝土梁最主要的受力来源，它包括静载荷和动载荷两种。

3. 混凝土梁的挠度混凝土梁在受到荷载作用时，会发生变形，其中最主要的是挠度。

挠度是指在梁的跨度方向上，梁在荷载作用下产生的弯曲变形。

三、挠度计算的基本原理混凝土梁的挠度计算，是基于弹性理论的。

根据弹性理论，混凝土梁的挠度可以分为两个部分，即由受拉钢筋引起的挠度和由混凝土引起的挠度。

其中，由受拉钢筋引起的挠度是根据受拉钢筋的应力计算得到的。

而由混凝土引起的挠度，则需要根据混凝土的应力分布和混凝土的本构关系来计算。

四、挠度计算的方法1. 受拉钢筋的挠度计算受拉钢筋的挠度计算，可以通过下面的公式来计算：δs = (5/384) x (qL^4)/(EI)其中，δs表示受拉钢筋的挠度，q表示荷载，L表示梁的跨度长度，E 表示受拉钢筋的弹性模量，I表示受拉钢筋的截面惯性矩。

2. 混凝土的挠度计算混凝土的挠度计算，可以通过下面的公式来计算：δc = (5/384) x (qL^4)/(EI) x β其中，δc表示混凝土的挠度，β表示混凝土的弯曲系数，它的取值范围是0.2~0.5。

3. 总挠度的计算混凝土梁的总挠度，即由受拉钢筋和混凝土共同引起的挠度，可以通过下面的公式计算：δ = δs + δc其中，δ表示混凝土梁的总挠度。

常数D表示起始截面的挠度×刚度(EI)
第八章 弯曲变形 /三、计算弯曲变形的两种方法
例题 一简支梁受力如图所示。试求 ( x), ( x) 和 , 。 A max F y 解： 1、求支座反力 x x C B A Fb Fa x FAy , FBy a b
L
L
L
2、分段列出梁的弯矩方程 AC段 (0 x a)
Fb( L2 b 2 ) A 0, 6 LEI
则由 解得：
C 1 x a
Fab(a b) 0( a b) 3LEI
0在AC段。
Fb 1 ( x ) [3x 2 ( L2 b 2 )] 0 6 LEI
x L2 b 2 3
D左 D右 连续条件： D左 D右 B左 B右
第八章 弯曲变形 /三、计算弯曲变形的两种方法
④积分常数的物理意义和几何意义
物理意义：将x=0代入转角方程和挠曲线方程，得 C 即坐标原点处梁的转角，它的 EI o EI倍就是积分常数C； 即坐标原点处梁的挠度的 EI倍就是积分常数D。 D EI o 几何意义：C——转角 D——挠度
第八章 弯曲变形 /三、计算弯曲变形的两种方法
例题：列出图示结构的边界条件和连续条件。
A 0 边界条件： A 0
连续条件：
B左 B右 B左 B右
第八章 弯曲变形 /三、计算弯曲变形的两种方法
例题：列出图示结构的边界条件和连续条件。
A 0 解：边界条件： A 0 C 0
答案 D
2、挠曲线的特征：光滑连续曲线(2)
FA＝0 FB＝0 MCD＝const
A C D B
答案 D

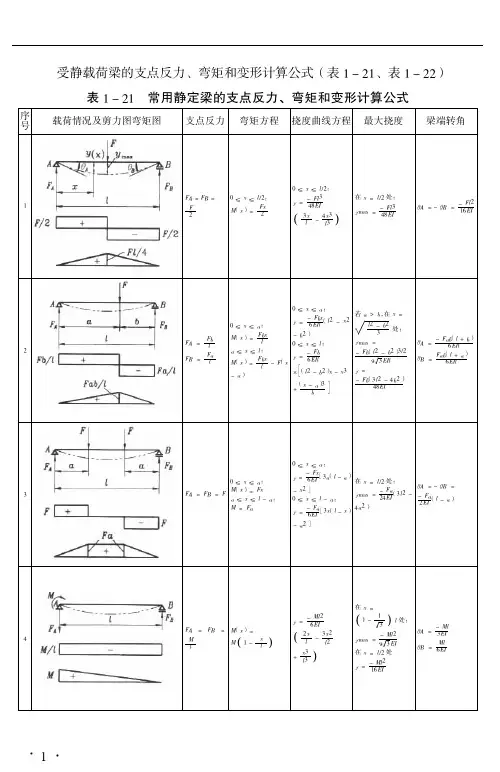
表1 简单载荷下基本梁的剪力图与弯矩图注：外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁2．单跨梁的力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EI w 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

[例1] 已知二跨等跨梁l ＝5m ，均布荷载q ＝11.76kN/m ，每跨各有一集中荷载F ＝29.4kN ，求中间支座的最大弯矩和剪力。

[解] M B 支＝（－0.125×11.76×52）＋（－0.188×29.4×5）＝（－36.75）＋（-27.64）＝－64.39kN ·mV B 左＝（－0.625×11.76×5）＋（－0.688×29.4）＝（－36.75）＋（－20.23）＝－56.98kN[例2] 已知三跨等跨梁l ＝6m ，均布荷载q ＝11.76kN/m ，求边跨最大跨中弯矩。

[解] M1＝0.080×11.76×62＝33.87kN ·m 。

2）三跨等跨梁的力和挠度系数 表2-12注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

x
x
0,
l 2
x
l 2
,
3l 2
EIw1
1 24
qx4
C1x
D1
EIw2
1 48
ql
3l 2
3
x
C2 x
D2
x
0,
l 2
x
l 2
,
3l 2
EIw1
1 6
qx3
C1
EIw2
1 16
ql
3l 2
2
x
C2
x
0,
l 2
x
l 2
,
3l 2
4 边界条件、连续条件 5 梁的转角方程和挠曲线方程
2
2 EIw(l) 0
EIw
1 6
qx3
ql 4
x2
C1
1 24
ql 4
ql 12
l3
C1l
D1
0
EIw
1 24
qx 4
ql 12
x3
C1x
D1
C1
ql 2 24
5 梁的转角方程和挠曲线方程
EIq 1 qx3 ql x2 ql3
6
4 24
EIw 1 qx4 ql x3 ql3 x 24 12 24
[f] L ~ L 500 600
普通机车主轴
[q ] 0.30
3，影响变形的因素
L 10时, Q的影响只有M的3% h
由小变形条件， x不计
4，计算变形的方法
积分法、 叠加法、 能量法、
………
9.2 挠曲线近似微分方程
1、挠曲线近似微分方程
1 M z (x)
EI z

ｄ ｘ Ｅ１ ２）
由 弯 曲 应 力 知 识， 可 知 Ｖ ＝
一
／
和
ｗ （ ｘ 、 ＝ｄ Ｖ／
对 （ ２）式 求导 可得
求梁位移和转角的积分法
在计 算梁 或轴任意截 面处 的位移和 转角前 ，若 能够
根 据 梁 的 受 力特 点 ，定 性 画 出 梁挠 曲线 的 大 致 形状 ， 可直
位移均为零 ，而固定和活动铰支座处的位移 为零 。 建立 Ｘ ， ｖ坐标轴 。ｘ轴必须平行于梁 变形前的轴线 ， 原点为梁上任意一点，正 向即可 向右也可向左。
当梁 上 作 用 多 个 不 连 续 载 荷 时 ，可 在 各 间 断 点 之 间
Ｖ＝ （ ） 梁 挠曲 线的数学表 达式为［ １ １ ， 由高 等数学
ｄ Ｖ
— —
ｆ
—— ————
＝
ｄ ｘ ＥＩ 对 （ ３） 式 求 导 可得
（ ３）
观 的展 示弯曲变形的计 算结果 ，并 有助于 判断计 算结 果是 否正确 。梁 弯曲后的轴 线 ，即梁截面形 心的连线 ，成 为梁 的挠曲线。一般 地 ，施加 约束力的约束 （ 如 铰 ）会限制梁 在 该处的线位移 。而产生约束力偶 的约束 （ 如固定端 ）会
中图分类号 ：Ｔ Ｂ １ ２ ５文献标识码 ：Ａ文章编号 ：１ ０ ０ ３ — ８ ９ ６ ５（ ２ ０ １ ３ ） ０ ４ — ０ ０ ７ ０ — ０ ２
在 实 际 工程 中 ，常 常 对 梁 和 轴 等 受 弯 构 件 的 变 形 有
一
定的限制要求 ，准确的计算梁或轴的转角及挠度 ，不仅
过程略 ）
：
弯矩 一曲率关系 （ 推导过略 ）
１ ｐ Ｅ