当前位置：文档之家 › 《材料力学》第5章-梁弯曲时的位移-习题解讲课教案

《材料力学》第5章-梁弯曲时的位移-习题解讲课教案

  • 格式：doc
  • 大小：2.23 MB
  • 文档页数：54

下载文档原格式

  / 54

合集下载

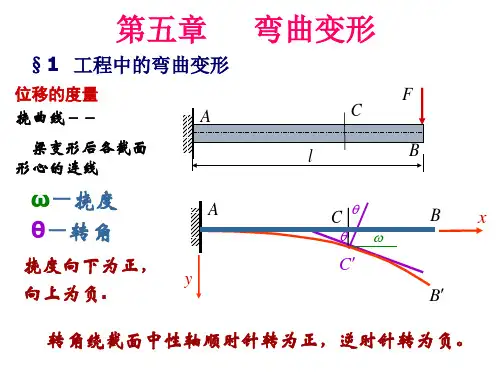
材料力学第5章弯曲变形ppt课件

材料力学第5章弯曲变形ppt课件

qL
4.22kNm
4.22kNm
M
max
32 M
max
76.4MPa
WZ
d 3
例题
20kN m
A
4m
FA
20kN m
A
MA
4m
试求图示梁的支反力
40kN
B
D
2m
2m
B
B1 FB
FB 40kN
B
D
B2
2m
2m
在小变形条件下,B点轴向力较小可忽略不
计,所以为一次超静定.
C
B1 B2
FBBBMF12AA2383qFEqELBqqLI84LI2LLZZ32F35BFF4FEFB83PBPLIEL7Z3L12IZ.218352.k75N5kFkN2PNmEL2IZ2
x
边界条件
A
L2
B
L2
C
y
连续条件
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
全梁仅一个挠曲线方程
C
q
EA
共有两个积分常数 边界条件
L1
A
x
B
EI Z
L
y
例题 5.5
用积分法求图示各梁挠曲线方程时,试问在列各梁 的挠曲线近似微分方程时应分几段;将分别出现几个 积分常数,并写出其确定积分常数的边界条件
q
a
B C LBC
B
2a
FN
B
q2a4
8EIZ
FN 2a3
3EIZ
C
FN
a
D

孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-梁弯曲时的位移(圣才出品)

孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-梁弯曲时的位移(圣才出品)
5 / 41
圣才电子书

ql3/6，D＝－ql4/24。
十万种考研考证电子书、题库视频学习平台
故挠曲线方程和转角方程分别为：
w（x）＝qx2（x2＋6l2－4lx）/（24EI），θ（x）＝q（x3－3lx2＋3l2x）/（6EI）
则最大挠度 wmax＝w（x）|x＝l＝ql4/（8EI）；梁端转角 θB＝θ（x）| x＝l＝ql3/（6EI）。
表 5-1-4 叠加原理计算梁的挠度和转角
四、梁的刚度校核·提高梁的刚度的措施（见表 5-1-5）
表 5-1-5 梁的刚度校核及提高措施
3 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台

五、梁内的弯曲应变能 定义：由于梁弯曲变形而存储的能量称为梁内的弯曲应变能。梁在弹性变形过程中，其 弯曲应变能与作用在梁上的外力所作的功相等，常见梁内的弯曲应变能见表 5-1-6。
则最大挠度 wmax＝w（x）|x＝l＝Fl3/3EI；梁端转角 θB＝θ（x）| x＝l＝Fl2/2EI。
图 5-2-1（a）（b） （2）建立如图 5-2-1（b）所示坐标系。 首先列弯矩方程：M（x）＝－q（l－x）2/2，由此可得挠曲线近似方程： EIw″＝－M（x）＝q（l－x）2/2 积分得： EIw′＝－q（l－x）3/6＋C① EIw＝q（l－x）4/24＋Cx＋D② 该梁的边界条件：x＝0，w＝0，x＝0，w'＝0。代入式①、②可确定积分常数：C＝
圣才电子书

十万种考研考证电子书、题库视频学习平台
第 5 章 梁弯曲时的位移
5.1 复习笔记
梁在承受荷载时发生相应的变形，变形后轴线相对原位置将会发生位移、梁的截面将出 现转角，梁内会因变形存储能量。本章首先介绍梁的位移概念，并基于坐标系统建立挠曲线 方程；接着介绍求解梁的位移的方法，根据挠曲线近似微分方程积分和按叠加原理计算；再 介绍梁刚度校核以及提高梁刚度的方法；最后介绍梁弯曲应变能的概念及计算方法。

材料力学第五章梁弯曲时的位移讲课文档

材料力学第五章梁弯曲时的位移讲课文档

()
请课后完成A处挠度的计算
wA
q0l 4 30EI
第五十五页，共98页。
例2图示平面折杆AB与BC垂直，在自由端C受集中力 P作用。已知各段弯曲刚度均为EI,拉伸刚度为EA 。试 用卡氏第二定理求截面C的水平位移和铅垂位移。
a
P
B
C
a
A
第五十六页，共98页。
解：1.计算C处铅垂位移
任意截面弯矩方程,轴力方程为
当梁上同时作用几个载荷时，各个载荷所引起的变 形是各自独立的，互不影响。
若计算几个载荷共同作用下在某截面上引起 的变形，则可分别计算各载荷单独作用下的 变形，然后叠加。
第三十二页，共98页。
如图示，要计算三种载荷作用下在某截面如C截面 挠度，则可直接查表：各载荷单独作用下的挠度 ，然后叠加（代数和）。
第十二页，共98页。
考虑小变形条件：
(1x)(1w w 2)3/2w
1 M(x)
(x) EIz
Ezw IM (x)
问题的关键：考虑上式中的取正还是取负？
第十三页，共98页。
问题的关键：考虑上式中的取正还是取负？
y M0 Mw0 M
y M0 M w0M
x
x
Ew IM
第十四页，共98页。
思考:与小挠度微分方程 （）
M(x1)P1x FN(x1)0
x2 B
P
x1
C
M(x2)Pa FN(x2)P
A
C ya 0M E (x 1 )I M P (x 1 )d1 x a 0F N E (x 1 )A F N P (x 1 )d1 x a 0M E (x2)IM (P x2)d2x a 0F N E (x2)A F N P (x2)d2x

《材料力学》第5章-梁弯曲时的位移-习题解

《材料力学》第5章-梁弯曲时的位移-习题解

第五章 梁弯曲时的位移 习题解[习题5-1] 试用积分法验算附录IV 中第1至第8项各梁的挠曲线方程及最大挠度、梁端转角的表达式。

解：序号1（1）写弯矩方程（2）写挠曲线近似微分方程，并积分 把边界条件：当0=x 时，0'=w，0=w 代入以上方程得：01=C，02=C。

故：转角方程为：x M EI EIw e ==θ'，EIxM e =θ 挠曲线方程：221x M EIw e =， EI x M w e 22=（3）求梁端的转角和挠度 解：序号2（1）写弯矩方程（2）写挠曲线近似微分方程，并积分 把边界条件：当0=x 时，0'=w，0=w 代入以上方程得：01=C，02=C。

故：转角方程为：2'21Fx Flx EI EIw -==θ，)2(22x lx EIF-=θ 挠曲线方程：326121Fx Flx EIw -=，)3(62x l EIFx w -=（3）求梁端的转角和挠度解：序号3（1）写弯矩方程当a x ≤≤0时， Fx Fa x a F x M +-=--=)()( 当l x a ≤≤时， 0)(=x M（2）写挠曲线近似微分方程，并积分当a x ≤≤0时，把边界条件：当0=x 时，0'=w，0=w 代入以上方程得：01=C，02=C。

故：转角方程为：2'21Fx Fax EI EIw -==θ，)2(22x ax EIF-=θ 挠曲线方程：326121Fx Fax EIw -=，)3(62x a EIFx w -=（3）求梁端的转角和挠度设集中力的作用点为C ，则：EI Fa a a a EI F a C 2)2(2)(22=-⋅==θθ EIFa a a EI Fa a w w C 3)3(6)(32=-== 由于CB 段没有外力作用，故该段没有变形，所以：EIFa B 22=θ)233(62)(3tan )(223a a x EIFa EI Fa a x EI Fa a x w w C C B +-=-+≈-+=θ )3(62a x EIFa w B -= 解：序号4（1）写弯矩方程 2)(21)(x l q x M --= （2）写挠曲线近似微分方程，并积分)("x M EIw -= 2")(21x l q EIw -=1322'6)()()(2)(2C x l q x l d x l q dx x l q EIw +--=---=-=⎰⎰ 当0=x 时，0'=w ，即：136)0(0C l q +--=，631ql C =66)(33'ql x l q EIw +--= 23433624)(6)()(6C x ql x l q x ql x l d x l q EIw ++-=+--=⎰ 当0=x 时，0=w 代入以上方程得：24240C ql +=，2442ql C -=24624)(434ql x ql x l q EIw -+-=故：转角方程为：66)(33'ql x l q EIw +--= 挠曲线方程：24624)(434ql x ql x l q EIw -+-=]4)[(24434l x l x l qEIw -+-=)4464(2443432234l x l x lx x l x l l q -++-+-= )46(244322x lx x l q +-= )46(24222x lx l qx +-= （3）求梁端的转角和挠度66)()(33'ql l l q EI l EIw B +--=θEIql B 63=θEIql l l l l ql EIw l EIw B 8)46(24)(4222=+⋅-==解：序号5（1）写弯矩方程l xl q x q -=0)(，lx l q x q )()(0-= lx l q x l l x l q x l x M 6)(3])()(21[)(300--=-⋅-⋅-⋅-=（2）写挠曲线近似微分方程，并积分)("x M EIw -= 30")(6x l lq EIw -=1403030'24)()()(6)(6C lx l q x l d x l l q dx x l l q EIw +--=---=-=⎰⎰ 当0=x 时，0'=w ，即：14024)0(0C l l q +--=，24301l q C =2424)(3040'l q l x l q EIw +--=23050304024120)(24)()(24C x l q l x l q x l q x l d x l l q EIw ++-=+--=⎰ 当0=x 时，0=w 代入以上方程得：250120)0(0C l l q +-=，120402l q C -=12024120)(403050l q x l q l x l q EIw -+-=故：转角方程为：2424)(3040'l q l x l q EIw +--=挠曲线方程：12024120)(403050l q x l q l x l q EIw -+-=)51010(120322320x lx x l l lx q EIw -+-=（3）求梁端的转角和挠度24)(30'l q EI l EIw B ==θ，EIl q B 2430=θ12024120)()(403050l q l l q l l l q EIw l EIw B -⋅+--==， EIl q w B 3040=解：序号6（1）写弯矩方程 l M R A B =（↑），lM R AA = （↓） x lM M x R M x M AA A A -=-=)( （2）写挠曲线近似微分方程，并积分)("x M EIw -= A AM x lM EIw -=" 12'2C x M x lM EIw A A +-=2123216C x C x M x l M EIw A A ++-=把边界条件：当0=x 时，0=w 代入以上方程得：02=C 。

材料力学第五章梁弯曲时的位移

材料力学第五章梁弯曲时的位移
第五章 梁弯曲时的位移
工程实例
7-1
工程实例
工程实例
5-1 梁的位移——挠度及转角
建立坐标系，oxy为梁对称面，外力作用在对 称面内。所以，挠曲线为o xy面内的平面曲线。
挠度
y 向下为正。
y
x
y
转角
x
挠曲线
挠曲线方程：
7-2
w= f (x)
挠度
略去剪力的影响，则平面假设成立，发
y
5.2 积分法求梁的挠度和转角
例1 求梁的转角方程和挠度方程，并求最大转角和最大挠度， 梁的EI已知。
解 1）由梁的整体平衡分析可得：
2）写出x截面的弯矩方程
FAx 0, FAy F (), M A Fl (
)
A
x
l
yB
F B
B
x
M ( x ) F (l x ) F ( x l )
A
FAx 0, FAy
Fb Fa , FBy l l
2）弯矩方程
FAy x1
ymax
x2
FBy
AC 段：
M x1 FAy x1 Fb x1 ,0 x1 a l
y
a
b
CB 段：
Fb M x2 FAy x2 F ( x2 a ) x2 F ( x2 a ), l
目录
a x2 l
5.2 积分法求梁的挠度和转角
A d 2 w1 Fb EI M ( x1 ) x1 2 dx1 l FAy x1 dw1 Fb 2 EI EI ( x1 ) x1 C1 x2 dx1 2l Fb 3 a EIw1 x C1 x1 D1 6l a x2 l CB 段： y d 2 w2 Fb EI M ( x2 ) x2 F ( x2 a) 2 dx2 l dw Fb 2 F EI 2 EI ( x2 ) x 2 ( x2 a ) 2 C 2 dx2 2l 2 Fb 3 F EIw2 x 2 ( x2 a)3 C2 x2 D2 6l 6

第五章 梁弯曲时的位移

第五章 梁弯曲时的位移
利用边界条件确定上面二式中的积分常数C 利用边界条件确定上面二式中的积分常数 1,C2,即可得 梁的挠度方程和转角方程
李田军材料力学课件 10 第五章 梁弯曲时的位移
积分法求解梁位移的思路: 积分法求解梁位移的思路: 建立合适的坐标系; ① 建立合适的坐标系; 求弯矩方程M(x) ; ② 求弯矩方程 ③ 建立近似微分方程: EIw′′ = M ( x ) 建立近似微分方程: 根据本书的规定坐标系,取负号进行分析. 根据本书的规定坐标系,取负号进行分析. ④ 积分求
李田军材料力学课件 9 第五章 梁弯曲时的位移
积分法求梁的变形 对于等刚度梁, 对于等刚度梁,梁挠曲线的二阶微分方程可写为
Ely'' = M(x)
对此方程连续积分两次,可得 对此方程连续积分两次,
Ely' (x) = ∫ M(x)dx + c1 Ely(x) = ∫ M(x)dxdx + c1x + c2
最大转角,显然在支座处
Pab θA =θ (0) = (L + b) 6EIz Pab θB =θ (L) = (L + a) 6EI 6EIz
P a L y
C
b B x
a >b a <b
θmax =θB θmax =θA
A
从A→B, θ + → 中间必经过0
李田军材料力学课件
19
第五章
梁弯曲时的位移
第五章 梁弯曲时的位移
梁的位移——挠度及转角 §5.1 梁的位移 挠度及转角 §5.2 梁的挠曲线近似微分方程及其积分 §5.3 按叠加原理计算梁的挠度和转角 *§5.4 梁挠曲线的初参数方程 § §5.5 梁的刚度校核.提高梁的刚度的措施 §5.6 梁内的弯曲应变能

材料力学上册第五章梁弯曲时的位移

材料力学上册第五章梁弯曲时的位移
6EIl
Mechanics of Materials
wmax 在AC段
wmax
=
Fb( l 2 − b2 )3 2 9 3EIl
Mechanics of Materials
例题：已知梁的刚度EI，用奇异函数法求梁的位移
θA、θD、wB、wD。
qa
q
A
B
C Dx
FA a
y
aa
FC
解：建立图示坐标系
1、求约束反力
( ) M(x) = − EI
w′′ 1+ w′2
32
Mechanics of Materials
若挠曲线是较平坦的光滑连续曲线， w′ << 1，
可忽略不计。
则
M (x) = −w′′
EI
即
EIw′′ = − M (x)
——挠曲线近似微分方程
适用条件： 线弹性小变形； 对称弯曲的细长梁。
2、积分法确定梁的位移
一、挠曲线近似微分方程
材力 数学
1 = M(x)
ρ EI
( ) 1 = w′′
ρ 1 + w′2 3 2
x y M > 0 w′′ < 0
( ) M(x) = ± EI
w′′ 1+ w′2
32
x
( ) M(x) = − EI
w′′ 1+ w′2
32
y M < 0 w′′ > 0
☻挠曲线微分方程的正负号与选取的坐标系有关
2
Mechanics of Materials
弯矩的通用方程
∑ ∑ ∑ ∑ ( ) M x =
i
Mi < x −ai >0 +

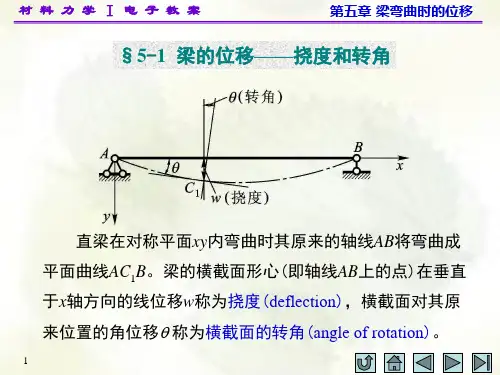
材料力学梁弯曲时的位移

材料力学梁弯曲时的位移

w
1 w2
3/ 2
M x
EI
由于梁的挠曲线为一平坦的曲线，上式中的w2与1相比可略
去，于是得挠曲线近似微分方程 w M x
EI
8
材料力学Ⅰ电子教案
第五章 梁弯曲时的位移
Ⅱ. 挠曲线近似微分方程的积分及边界条件
w M x
EI 求等直梁的挠曲线方程时可将上式改写为
EIw M x
后进行积分，再利用边界条件(boundary condition)确定积分 常数。
左段梁 (0 x a)
右段梁 (a x l)
q1
w1
Fb 2lEI
1 3
l2 b2
x
2
q2
w2
Fb 2lEI
l b
x
a
2
x2
1 3
l2
b2
w1
Fbx 6lEI
l2
b2
x2
w2
Fb 6lEI
l b
x
a
3
x3
l2
b2
x
30
材料力学Ⅰ电子教案
第五章 梁弯曲时的位移
于是有
C2 0
及
EIw|xl
q 2
l4 6
l4 12
C1l
0
即
C1
ql3 24
，C2
0
从而有
转角方程 q w q l3 6lx2 4x3 24EI
挠曲线方程 w qx l3 2lx2 x3 24EI
22
材料力学Ⅰ电子教案
第五章 梁弯曲时的位移
根据对称性可知，两支座处的转角qA及qB的绝对值相
F lx
x2 2
C1
EIw

材料力学课件5第五章梁弯曲时的位移5-1

材料力学课件5第五章梁弯曲时的位移5-1

F A
x
θmax
l
wmax
y
B o
F A
o
B
l
y
x
请大家将坐标原点取在固定端，练习完 整解题过程。
例题5-2 试求图示等直梁的挠曲线方程和转角方 程，并确定其最大挠度wmax和最大转角max。
解：该梁的弯矩方程为
ql 1 2 q M x x qx lx x 2 2 2 2
Fb x2 =EI w1 +C1 (1) l 2 Fb x3 EI w1 = +C1 x D1 (2) l 6
Fb x2 F(x-a) 2 EI w + +C 2 (3) 2 = l 2 2 Fb x3 F(x-a) 3 EI w 2 = + +C 2 x D2 (4) l 6 6
截面x的位移—挠度、转角 转角 θ C 1 θ w C
1
挠度
A
x y
B
x
挠曲线
梁变形前后横截面形心位置的变化称 为位移，位移包括线位移和角位移。在小 变形和忽略剪力影响（l >> h）的条件下， 略去x 方向的线位移，y 方向的线位移是截 面形心沿垂直于梁轴线方向的位移，称为 挠度，用 w 表示，单位m、mm；角位移 是横截面变形前后的夹角，称为转角，用 θ 表示，单位弧度。而变形后的轴线是一 条光滑连续平坦的曲线称为挠曲线（弹性 曲线） 。
w'(l )=0 代入（1）: Fl 2 / 2+C1 = 0 得：C1=－ Fl 2 / 2
w(l ) =0 代入（2）： Fl 3/ 6+C1l+C2 = 0
C2= -Fl 3/ 6 -C1l = -Fl 3/ 6 + Fl 3 / 2 = Fl 3/ 3

材料力学第五章梁弯曲时的位移课件

材料力学第五章梁弯曲时的位移课件
qw q0 (l39lx 28x3)
4E 8I
w(0)0 q (0) q0l3
48EI
固定铰支座 活动铰支座
w(l)0 q(l) 0
固定端 活动铰支座
材料力学第五章梁弯曲时的位移
22
M (x)Ew Iq0(3lx 4x2) 抛物线 8
FS(x)ddM xq 80(3l8x)
直线
q(x)dFS dx
材料力学第五章梁弯曲时的位移
12
x
FA
x
FA
Fb l
FB
FB
Fa l
AD段（ 0≤ x ≤ a ）：
M1(x)
Fbx l
DB段（ a ≤ x ≤ l ）：
M2(x)F l b xF(xa)
材料力学第五章梁弯曲时的位移
13
x a AD段（ 0≤ ≤ ）：
M1(x)
Fbx l
EIw1
Fbx l
Ew I1 EqI1F l bx22C1
q0
M(0)0
FS(0)
3 8
q0l
M(l) 81q0l2
FS(l) 85q0l
材料力学第五章梁弯曲时的位移
23
q0
1 8
q0l
材料力学第五章梁弯曲时的位移
7
挠曲线上某些点的已知位移（挠度和 转角）条件 —— 边界条件
wA ＝ 0 wB ＝ 0
wA ＝ 0 qA ＝ 0
边界条件 —— 支座处的约束条件
材料力学第五章梁弯曲时的位移
8
挠曲线的任意点上，有唯一确定的挠 度和转角 —— 连续条件
错！
错！
当弯矩方程需要分段建立时，在相邻梁 段的交接处，应具有相同的挠度和转角。

材料力学I-第5章%20梁弯曲时的位移[1]

材料力学I-第5章%20梁弯曲时的位移[1]


T$
T%
$
Z'
Z&
'
D
)$ )%
TD[ T[ d [ d D TD [ D T[ 0 [ TD[ D d [ d D , Z c (,Zc 0 [ TD[ T[ d [ d D c (,Z TD[ T[ & (,Z TD[ T[ & [ ' Z c (,Zc 0 [ TD[ TD [ D T[ D d [ d D c (,Z TD[ TD [ D T[ & (,Z TD[ TD [ D T[ & [ ' 0 [


0H
O
0H
G Z )O )[ G[ (, GZ )O[ )[ & G[ (, Z )O[ )[ &[ ' (, T & Z '


0
)O )[
T$ T%
T O

ZPD[
)$
[ TO 0 [ )$ [ T [ [ T O[ [ O [ T O[ O
(,Zcc (,Zc (,Z
& '
O T O O
)$
$ O
%
T O
Z

[
(,Z
&
[ D

&
TD ' T Z

材料力学(土木类)第五章 梁弯曲时的位移(2)专用课件_570

材料力学(土木类)第五章 梁弯曲时的位移(2)专用课件_570

F
·
F2l3
(b)
wD1
直线
D1
wD1 D1 BD
wD2
wB2
3EI
B2
D2

P 2l 2 2EI
同理可得此时B截面的挠度和转角为：
w B 2w D 2D 2B D 8 3 F E 3 lI4 2 F E 2llI 1 3 E F 4 3（lI向下）
B2
wB1 B1
Fl 3 wC1 3EI
C1

Fl 2 2 EI
由位移关系可得此时B截面的挠度和转角为：
w B 1w C 1C 1B C 3 F E 3 lI2 F E 2 lI 2 l4 3 F E 3（lI向下）
B1
C1

Fl2 2EI
（顺时针）
对图b，可得D截面的挠度和转角为：

qa2a3
48EI
B1
qa2a2
16EI
图d中D截面的挠度和B截面的转角为：
wD2

2qa4 16EI
B2

qa 3 3 EI
将相应的位移进行叠加，即得：
w Dw D 1w D 26 qE 4a I8 qE4a I2qE 4 4aI （向下）
BB 1 B 2q 12 E a a 6 2 I3 q E 3a I1 qE 3 2 a （I顺时针）
面的挠度和转角以及D截面的挠度。
F=qa
A
EI D
B
C
a
a
a
解：可将外伸梁看成是图a和b所示的简支梁和悬臂 梁的叠加。
A
F=qa EI
qa qa2/2
D
B
B
C
(a)

第五章梁弯曲时的位移

第五章梁弯曲时的位移
挠曲线方程为 w w(x)
式中 ，x 为梁变形前轴线上任一点的横坐标 ，w 为该点的挠度。
A
挠曲线
y
CB
x
w挠度
C'
转角
5
三、挠度与转角的关系：
A
挠曲线
y
CB
x
w挠度
C'
转角
tg w' w'(x)
6
四、挠度和转角符号的规定 挠度：向下为正，向上为负。 转角：自 x 转至 切线方向，顺时针转为正，逆时针转为负。
b
l
FB
两段梁的弯矩方程分别为
b M1 FA x F l x
(0 x a)
b M2 F l x F(x a) (a x l)
36
两段梁的挠曲线方程分别为
挠曲线方程
1 ( 0 x a)
EIw1"
M1
F
b l
x
转角方程 挠度方程
EIw1'
F
b l
x2 2
C1
EIw1
F
b l
x3 6
l
EIw Fl
46
l
F x
b(x)
b1
bmax h
EIw Fl
EIw Flx C
EIw Fl x2 Cx D 2
47
l
F x
b(x)
b1
bmax h
EIw Flx C
EIw Fl x2 Cx D 2
边界条件： x l , w 0
xl , w0
48
l
F x
b(x)
b1
w2 与 1 相比十分微小而可以忽略不计, 故上式可近似为

材料力学第五章 梁的变形

材料力学第五章 梁的变形

连续条件
xa
wB1 wB2
例题 画出挠曲线大致形状。图中C为中间铰。
解： 边界条件
A
C
F
B
wA 0 qA 0
wB 0
两根梁由中间铰连接，挠
曲线在中间铰处，挠度连
续，但转角不连续。
wC左 wC右
qC左 qC右
A
挠曲线的凸向由弯矩的正
负号决定，正弯矩向下凸，
负弯矩向上凸。
例 图示等截面梁，弯曲刚度EI。设梁下有一曲面 y Ax3 ，欲
)
6l
bF l
F
b
C
Bx
x l
aF FRB l
AC段 (0 x a)
EIw1
bF l
x
EIw1
bF 2l
x2
C1
EIw1
bF 6l
x3
C1 x
D1
CB段 (a x l)
EIw2
bF l
x
F(x a)
EIw2
bF 2l
x2
F ( x a)2 2
C2
EIw2
bF 6l
x3
F ( x a)3 6
转角方程，挠度方程
EIw M ( x)
q w m 6lx 3x2 2l 2 6EIl A
m
l
C
w mx 3lx x2 2l 2 6EIl
2 m
y FRA l
l
x B
m FRB l
求 wmax w q 0
3 x0 1 3 l 0.423l
wmax
w
x0
F2 60kN
C
A
F1 200kN
F2
D

材料力学I第五章 ppt课件

材料力学I第五章 ppt课件

材料力学(Ⅰ)电子教案
梁弯曲时的位移
14
例题 5-1
试求图示悬臂梁的挠曲线方程和转角方程，
并确定其最大挠度wmax和最大转角qmax。梁的EI
为常量。
材料力学(Ⅰ)电子教案
梁弯曲时的位移
15
例题 5-1
解: 1. 列挠曲线近似微分方程，并积分。该梁的弯矩方 程为
M x F l x ( 1 )
挠曲线近似微分方程为
(b)
E w M I x F l x ( 2 )
通过两次积分得 Ew IFlx x 22C 1 (3) EI F w l2 x 2x 6 3 C 1xC 2 (4)
材料力学(Ⅰ)电子教案
梁弯曲时的位移
16
例题 5-1
2. 确定积分常数，并求转角方程和挠曲线方程
相比可略去，于是得挠曲线近似微分方程
w Mx
EI
材料力学(Ⅰ)电子教案
梁弯曲时的位移
10
II. 挠曲线近似微分方程的积分及边界条件
w Mx
EI 求等直梁的挠曲线方程时可将上式改写为
E w I M x
后进行积分，再利用边界条件(boundary condition) 确定积分常数。
材料力学(Ⅰ)电子教案
该梁的边界条件为：在 x =0 处 w'=0 ，w =0
由(3)、(4)两式得 C 10 ， C 20
将C1和C2代入(3)、(4)两式，得
转角方程
qwFxF l 2x(5)
EI2EI
挠曲线方程
F2lx F3x w
(6)
2EI6EI
材料力学(Ⅰ)电子教案
梁弯曲时的位移
17
例题 5-1
转角方程

材料力学课件第5章 弯曲位移

材料力学课件第5章 弯曲位移
此式称为 梁的挠曲线近似微分方程（differential equation of the deflection curve） 近似原因 : （1） 略去了剪力的影响; （2） 略去了 w2项; （3） tan w w( x )
§5-3 用积分法求弯曲变形 （Beam deflection by integration )
一、微分方程的积分 （Integrating the differential equation )
d 2ω M(x) 2 dx EI Z
若为等截面直梁, 其抗弯刚度EI为一常量上式可改写成
EIw M(x)
1.积分一次得转角方程 （The first integration gives the equation for the slope）
A C B x
C'
挠曲线
w挠度（

B
转角
4.挠度与转角的关系 （Relationship between deflection and slope）：
tan w ' w '( x )
A
C C'
挠曲线
B
x
w挠度
转角

B
5.弯曲位移计算的小变形假定
a.梁轴线在变形前后不产生伸缩，即长度不变
Fab( l b ) A 1 | x 0 6lEI Fab( l a ) B 2 | x l 6lEI
转角方程
b x F ( x a) C2 EIw 2 F l 2 2
2
2
挠度方程
b x3 F ( x a) C 2x D 2 EIw 2 F l 6 6

材料力学第五章 梁弯曲时的位移 PPT

材料力学第五章 梁弯曲时的位移 PPT

M(x) E Iz
高等数学：
1
r (x)
=±（1＋ww2）3/2
± w w （1＋ 2）3/2
=
M(x) E Iz
M ＜ 0，w ＞ 0
M ＞ 0，w ＜ 0
取负号!
－ w w （1＋ 2）3/2
=
M(x) E Iz
w w （1＋ 2）3/2
=－
M(x) E Iz
挠曲线微分方程
小 变 形
w
=－
DB段（a≤x≤l）： M2(x)F l b xF(xa) Ew I2 Fl b xF(xa)
q E w 2 IE2I F l b x 2 2 F (x 2 a )2 C 2
E2 I w F l b x 6 3F(x 6 a )3 C 2xD 2
确定积分常数 连续条件
x = a 时：
w1 w2 w1 w2
边界条件
x = 0 时： w1 0 x = l 时： w2 0
D1D20 C1C2F 6lb(l2b2)
AD段（ 0≤ x ≤ a ）：
w 1 q1F(6 b lE 2b I2)l2F Eb Ix2l
w1F(6 b lE 2b I2l)x6F EbIx3 l
DB段（ a ≤ x ≤ l ）：
q w 2 2 F ( 6 lE 2 b b 2 I ) l2 F Ex b 2 I l 2 F E (x I a )2
对于受任意荷载的简支梁，若挠曲线上无拐点， 则可用梁中点的挠度代替最大挠度。
例3：悬臂梁如图，已知F、a，M＝0.5 Fa，
梁的弯曲刚度 EI 为常数，试画出挠曲线的大致形 状。
FM
A
B
C
D
a
a

材料力学第五章梁弯曲时的位移分析

材料力学第五章梁弯曲时的位移分析

a)2
C2 x2 D2
C2
B B x
FBy
目录
5.2 积分法求梁的挠度和转角
4）由边界条件确定积分常数
位移边界条件
x1 0, w1(0) 0 x2 l, w2 (l) 0
光滑连续条件
x1 x2 a, 1(a) 2 (a)
x1 x2 a, w1(a) y2 (a) 代入求解，得
x1 ,0
x1
a
y
CB 段：
M x2
FAy
x2
F ( x2
a)
Fb l
x2
F ( x2
a),
a x2 l
目录
5.2 积分法求梁的挠度和转角
3）列挠曲线近似微分方程并积分
F
AC 段： 0 x1 a
EI
d 2w1 dx12
M (x1)
Fb l
x1
EI
dw1 dx1
EI (x1)
Fb 2l
x2 1
EI dw EI 1 F (l x)2 C
dx
2
EIw 1 F (l x)3 Cx D 6
代入求解
C 1 Fl2, D 1 Fl3
2
6
5）确定转角方程和挠度方程
EI 1 F (l x)2 1 Fl2
2
2
Ax
y
yB
l
F Bx
B
EIw 1 F (l x)3 1 Fl2x 1 Fl3
目录
5.2 积分法求梁的挠度和转角
例2 求梁的转角方程和挠度方程，并求最大转角和最大挠度，
梁的EI已知，l=a+b，a>b。
F
解 1）由梁整体平衡分析得：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《材料力学》第5章-梁弯曲时的位移-习题解第五章 梁弯曲时的位移 习题解[习题5-1] 试用积分法验算附录IV 中第1至第8项各梁的挠曲线方程及最大挠度、梁端转角的表达式。

解：序号1 （1）写弯矩方程 e M x M -=)(（2）写挠曲线近似微分方程，并积分 )("x M EIw -= e M EIw =" 1'C x M EIw e += 21221C x C x M EIw e ++=把边界条件：当0=x 时，0'=w ，0=w 代入以上方程得：01=C ，02=C 。

故：转角方程为： x M EI EIw e ==θ'，EIxM e =θ 挠曲线方程：221x M EIw e =， EI x M w e 22=（3）求梁端的转角和挠度EIlM l e B ==)(θθ EIl M l w w e B 2)(2==解：序号2 （1）写弯矩方程Fx Fl x l F x M +-=--=)()(（2）写挠曲线近似微分方程，并积分 )("x M EIw -= Fx Fl EIw -="12'21C Fx Flx EIw +-= 21326121C x C Fx Flx EIw ++-=把边界条件：当0=x 时，0'=w ，0=w 代入以上方程得：01=C ，02=C 。

故：转角方程为：2'21Fx Flx EI EIw -==θ，)2(22x lx EIF-=θ 挠曲线方程：326121Fx Flx EIw -=， )3(62x l EI Fx w -= （3）求梁端的转角和挠度EI Fl l l l EI F l B 2)2(2)(22=-⋅==θθ EIFl l l EI Fl l w w B 3)3(6)(32=-==解：序号3 （1）写弯矩方程当a x ≤≤0时， Fx Fa x a F x M +-=--=)()( 当l x a ≤≤时， 0)(=x M（2）写挠曲线近似微分方程，并积分当a x ≤≤0时， )("x M EIw -= Fx Fa EIw -="12'21C Fx Fax EIw +-= 21326121C x C Fx Fax EIw ++-=把边界条件：当0=x 时，0'=w ，0=w 代入以上方程得：01=C ，02=C 。

故：转角方程为：2'21Fx Fax EI EIw -==θ，)2(22x ax EIF-=θ 挠曲线方程：326121Fx Fax EIw -=， )3(62x a EI Fx w -=（3）求梁端的转角和挠度 设集中力的作用点为C ，则：EI Fa a a a EI F a C 2)2(2)(22=-⋅==θθ EIFa a a EI Fa a w w C 3)3(6)(32=-== 由于CB 段没有外力作用，故该段没有变形，所以：EIFa B 22=θ)233(62)(3tan )(223a a x EIFa EI Fa a x EI Fa a x w w C C B +-=-+≈-+=θ )3(62a x EIFa w B -= 解：序号4（1）写弯矩方程2)(21)(x l q x M --=（2）写挠曲线近似微分方程，并积分)("x M EIw -= 2")(21x l q EIw -=1322'6)()()(2)(2C x l q x l d x l q dx x l q EIw +--=---=-=⎰⎰ 当0=x 时，0'=w ，即：136)0(0C l q +--=，631ql C =66)(33'ql x l q EIw +--= 23433624)(6)()(6C x ql x l q x ql x l d x l q EIw ++-=+--=⎰ 当0=x 时，0=w 代入以上方程得：24240C ql +=，2442ql C -=24624)(434ql x ql x l q EIw -+-=故：转角方程为：66)(33'ql x l q EIw +--= 挠曲线方程：24624)(434ql x ql x l q EIw -+-= ]4)[(24434l x l x l qEIw -+-=)4464(2443432234l x l x lx x l x l l q -++-+-= )46(244322x lx x l q +-= )46(24222x lx l qx +-= （3）求梁端的转角和挠度66)()(33'ql l l q EI l EIw B +--=θEIqlB63=θEIqlllllqlEIwlEIwB8)46(24)(4222=+⋅-==解：序号5（1）写弯矩方程lxlqxq-=)(，lxlqxq)()(0-=lxlqxllxlqxlxM6)(3])()(21[)(3--=-⋅-⋅-⋅-=（2）写挠曲线近似微分方程，并积分)("xMEIw-=3")(6xllqEIw-=1433'24)()()(6)(6ClxlqxldxllqdxxllqEIw+--=---=-=⎰⎰当0=x时，0'=w，即：1424)0(0Cllq+--=，2431lqC=2424)(34'lqlxlqEIw+--=23050304024120)(24)()(24C x l q l x l q x l q x l d x l l q EIw ++-=+--=⎰ 当0=x 时，0=w 代入以上方程得：250120)0(0C l l q +-=，120402l q C -=12024120)(403050l q x l q l x l q EIw -+-=故：转角方程为：2424)(3040'l q l x l q EIw +--= 挠曲线方程：12024120)(403050l q x l q l x l q EIw -+-=)51010(120322320x lx x l l lx q EIw -+-=（3）求梁端的转角和挠度24)(30'l q EI l EIw B ==θ，EIl q B 2430=θ12024120)()(403050l q l l q l l l q EIw l EIw B -⋅+--==， EIl q w B 3040=解：序号6（1）写弯矩方程l M R A B =（↑），lMR A A = （↓） x lM M x R M x M AA A A -=-=)( （2）写挠曲线近似微分方程，并积分)("x M EIw -= A AM x lM EIw -=" 12'2C x M x lM EIw A A +-=2123216C x C x M x l M EIw A A ++-=把边界条件：当0=x 时，0=w 代入以上方程得：02=C 。

当l x =时，0=w 代入以上方程得： l C l M l l M A A 1232160+-⋅=，31lM C A = 故：转角方程为：322'lM x M x l M EIw A A A +-=挠曲线方程：x l M x M x l M EIw A A A 321623+-=)23(622l lx x lx M EIw A +-=)2)((6x l x l lxM EIw A --=（3）求梁端的转角和挠度 3)0('l M EI EIw A A ==θ， EIlM A A 3=θ632)(2'l M l M l M l l M EI l EIw A A A A B -=+-==θ， EIlM A B 6-=θ 16)22)(2(62)2(2l M l l l l l lM EIw lEIw A AC =--==， EI l M w A C162=解：序号7（1）写弯矩方程 l M R B A =（↑）， lMR B B = （↓） x lM x R x M BA ==)( （2）写挠曲线近似微分方程，并积分)("x M EIw -= x lM EIw B-=" 12'2C x lM EIw B +-= 2136C x C x lM EIw B ++-= 把边界条件：当0=x 时，0=w 代入以上方程得：02=C 。

当l x =时，0=w 代入以上方程得：l C l l M B 1360+-=，61lM C B = 故：转角方程为：622'lM x l M EIw B B +-= 挠曲线方程：)(666223x l lx M x l M x l M EIw B B B -=+-=（3）求梁端的转角和挠度 6)0('l M EI EIw B A ==θ， EIl M B A 6=θ 362)(2'l M l M l l M EI l EIw B B B B -=+-==θ， EIlM B B 3-=θ 16)4(62)2(222l M l l l lM EIw lEIw B AC =-==， EI l M w B C162=解：序号8（1）写弯矩方程2qlR R B A == （↑） 2221221)(qx x ql qx x R x M A -=-=（2）写挠曲线近似微分方程，并积分)("x M EIw -= 2"212qx x ql EIw +-=132'64C x q x ql EIw ++-=21432412C x C x q x ql EIw +++-=把边界条件：当0=x 时，0=w 代入以上方程得：02=C 。

当l x =时，0=w 代入以上方程得：l C l q l ql 14324120++-=，2431ql C =故：转角方程为：2464332'ql x q x ql EIw ++-=挠曲线方程：)2(24242412323343x lx l qx x ql x q x ql EIw +-=++-=（3）求梁端的转角和挠度24)0(3'ql EI EIw A ==θ， EIql A 243=θ242464)(3332'ql ql l q l ql EI l EIw B -=++-==θ， EIql B 243-=θ3845)842(242)2(4323ql l l l l lq EIw l EIw C =+⋅-⋅==， EI ql w C 38454=[习题5-2] 简支梁承受荷载如图所示，试用积分法求A θ，B θ，并求max w 所在截面的位置及该截面挠度的算式。