材料力学 梁弯曲时的位移谜底
- 格式:pdf
- 大小:282.35 KB
- 文档页数:7
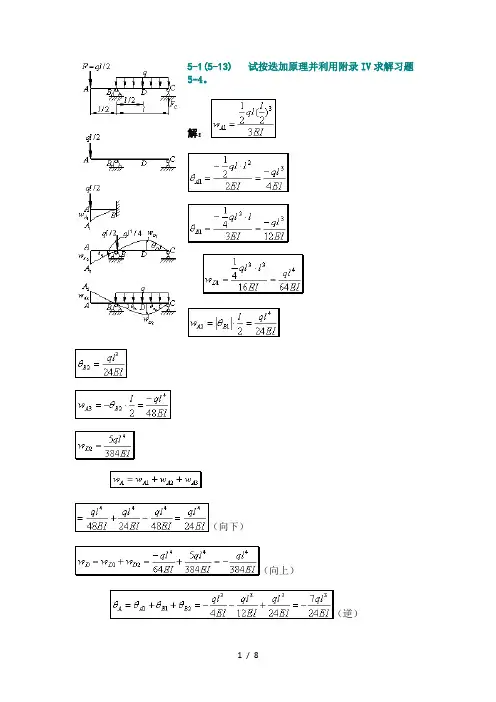
5-1(5-13)试按迭加原理并利用附录IV求解习题5-4。
解:返回5-2(5-14) 试按迭加原理并利用附录IV求解习题5-5。
解:分析梁的结构形式,而引起BD段变形的外力则如图(a)所示,即弯矩与弯矩由附录(Ⅳ)知,跨长l的简支梁的梁一端受一集中力偶M作用时,跨中点挠度为C的挠度返回5-3(5-15) 试按迭加原理并利用附录IV求解习题5-10。
解:返回5-4(5-16) 试按迭加原理并利用附录IV求解习题5-7。
解:原梁可分解成图5-16a和图5-16d迭加,而图5-16a又可分解成图5-16b和5-16c。
由附录Ⅳ得返回5-5(5-18)试按迭加原理求图示梁中间铰C处的挠度并描出梁挠曲线的大致形状。
已知EI为常量。
解:(a)由图5-18a-1(b)由图5-18b-1=返回5-6(5-19)试按迭加原理求图示平面折杆自由端截面C的铅垂位移和水平位移。
已知杆各段的横截面面积均为A,弯曲刚度均为EI。
解:返回5-7(5-25)松木桁条的横截面为圆形,跨长为4m,两端可视为简支,全跨上作用有集度为木的许用应力可相对挠度为条可视为等直圆木梁计算,直径以跨中为准。
)解:均布荷载简支梁,其危险截面位于跨中点,最大弯矩为强度条件有从满足强度条件,得梁的直径为对圆木直径的均布荷载,简支梁的最大挠度而相对挠度为由梁的刚度条件有为满足梁的刚度条件,梁的直径有由上可见,为保证满足梁的强度条件和刚度条件,圆木直径需大于返回5-8(5-26) 图示木梁的右端由钢拉杆支承。
已知梁的横截面为边长等于0.20m的正方形,解:从木梁的静力平衡,易知钢拉杆受轴向拉力于是拉杆的伸长木梁由于均布荷载产生的跨中挠度梁中点的铅垂位移的和,即。

孙训⽅材料⼒学第五版课后习题答案详解Microsoft Corporation孙训⽅材料⼒学课后答案[键⼊⽂档副标题]lenovo[选取⽇期]第⼆章轴向拉伸和压缩2-1? 2-2? 2-3? 2-4? 2-5? 2-6? 2-7? 2-8? 2-9 下页2-1? 试求图⽰各杆1-1和2-2横截⾯上的轴⼒,并作轴⼒图。
(a)解:;;(b)解:;;(c)解:;。
(d)解:。
返回2-2 ?试求图⽰等直杆横截⾯1-1,2-2和3-3上的轴⼒,并作轴⼒图。
若横截⾯⾯积,试求各横截⾯上的应⼒。
解:返回2-3?试求图⽰阶梯状直杆横截⾯1-1,2-2和3-3上的轴⼒,并作轴⼒图。
若横截⾯⾯积,,,并求各横截⾯上的应⼒。
解:返回2-4? 图⽰⼀混合屋架结构的计算简图。
屋架的上弦⽤钢筋混凝⼟制成。
下⾯的拉杆和中间竖向撑杆⽤⾓钢构成,其截⾯均为两个75mm×8mm的等边⾓钢。
已知屋⾯承受集度为的竖直均布荷载。
试求拉杆AE和EG横截⾯上的应⼒。
解:=1)? 求内⼒取I-I分离体?得? (拉)取节点E为分离体,故(拉)2)求应⼒75×8等边⾓钢的⾯积A=11.5 cm2(拉)(拉)2-5(2-6)? 图⽰拉杆承受轴向拉⼒,杆的横截⾯⾯积。
如以表⽰斜截⾯与横截⾯的夹⾓,试求当,30,45,60,90时各斜截⾯上的正应⼒和切应⼒,并⽤图表⽰其⽅向。
解:2-6(2-8) ?⼀⽊桩柱受⼒如图所⽰。
柱的横截⾯为边长200mm的正⽅形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的⾃重,试求:(1)作轴⼒图;(2)各段柱横截⾯上的应⼒;(3)各段柱的纵向线应变;(4)柱的总变形。
解:? (压)(压)返回2-7(2-9) ?⼀根直径、长的圆截⾯杆,承受轴向拉⼒,其伸长为。
试求杆横截⾯上的应⼒与材料的弹性模量E。
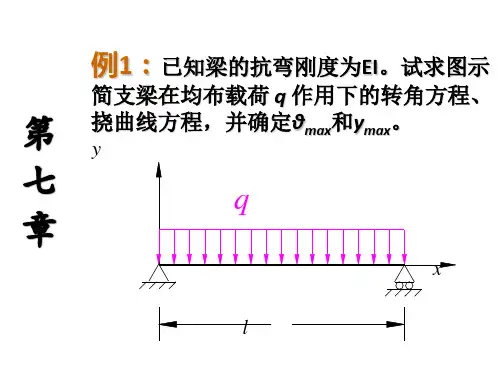
解:2-8(2-11) ?受轴向拉⼒F作⽤的箱形薄壁杆如图所⽰。
已知该杆材料的弹性常数为E,,试求C与D两点间的距离改变量。
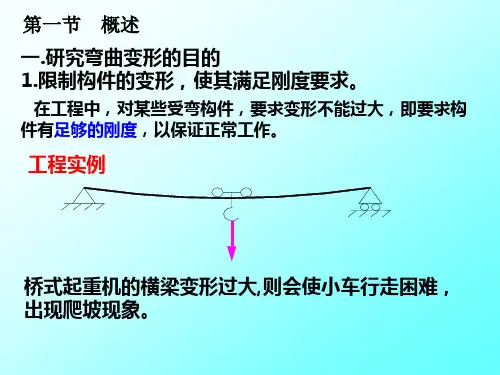



第六章梁弯曲时的位移§6.1 概述§概述研究变形的目的1. 限制弯曲变形,建立刚度条件;限制弯曲变形建立刚度条件2利用弯曲变形以便能够缓冲减振;2. 利用弯曲变形,以便能够缓冲、减振;3. 解静不定问题。
钢板轧机:轧辊压轧钢板汽车轮轴上的叠板弹簧§6.2梁的挠曲线近似微分方程§6.2 梁的挠曲线近似微分方程θCB ′′ABw CC F xC通常用横截面的两个基本位移量来反映梁的变形情况一、挠度和转角通常用横截面的两个基本位移量,来反映梁的变形情况11. 挠度w 2. 转角θ转y挠曲线′θCθCB C ′ABxw CC Fx——1. w 横截面形心在垂直于x 轴方向的线位移挠度小变形,挠度远小于跨长,形心沿x 轴方向的线位移与挠度相比属于高阶微量,可略去不计挠曲线方程w = f (x )挠曲线是一条光滑连续的曲线——横截面对其原来位置的角位移2. 转角θ(弹性曲线)(绕中性轴转过的角度)横截面的转角= 由x 轴转到曲线对应点处切线方向的夹角横截(锐角)x = 0,x = l,,)(当a > b()时最大挠度当a > b 时,最大挠度1==dw 应在AC 段内,令01θdx 得因此,工程计算中,不论受什么荷载作用,只要简支梁的挠曲即使荷载非常靠近右支座这种极端情况下,最大挠度所在位置仍与跨中位置非常靠近,w max 与w 跨中相差≤3%线上没有拐点(即挠曲线向一边弯),都可以用w max ←w 跨中积分法求梁的变形积分常数的确定:边界条件,连续条件优点:可全面表达挠度和转角缺点:方程与坐标选择有关;计算量大。
通常只关心某些特殊截面的挠度和转角:1. 简单荷载作用下,基本形式的静定梁某些特殊截面的挠度和转角的结果列出来用时直接查表2.某些特殊截面的挠度和转角的结果列出来,用时直接查表。
2.复杂情况(例,多个荷载作用或组合梁)可以采用叠加法。
叠加法求梁的位移1. 叠加原理:当所求参数(内力、应力或位移)与梁上荷载为线性关系时,由几项荷载共同作用时所引起的某一参数,就等于每项荷载单独作用时所引起的该参数值的代数和叠加适用条件:所求物理量必须与荷载成线性正比关系前提:线弹性、小变形各荷载的作用互不相干,互不影响2. 方法(1)分解每种情况都是简单模型;——(2)分别计算——查表;(3)叠加。


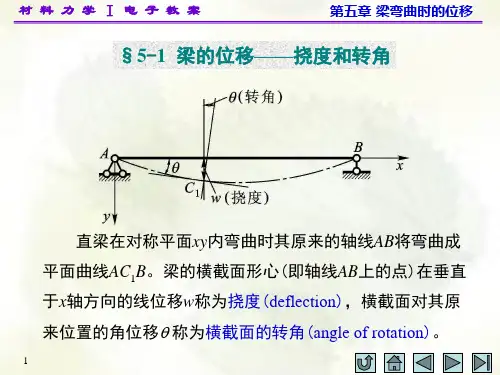

材料力学(土)笔记第五章 梁弯曲时的位移1.梁的位移——挠度及转角为研究等直梁在对称弯曲时的位移取梁在变形前的轴线为x 轴,梁横截面的铅垂对称轴为y 轴而xy 平面即为梁上荷载作用的纵向对称平面梁发生对称弯曲变形后,其轴线将变成在xy 平面内的曲线1AC B度量梁变形后横截面位移的两个基本量是挠度:横截面形心(即轴线上的点)在垂直于x 轴方向的线位移ω转角:横截面对其原来位置的角位移θ 梁变形后的轴线是一条光滑的连续曲线,且横截面仍与该曲线保持垂直因此横截面的转角θ也就是曲线在该点处的切线与x 轴之间的夹角度量等直梁弯曲变形程度的是曲线的曲率梁的变形还受到支座约束的影响通常就用这两个位移量来反映梁的变形情况梁轴线弯曲成曲线后,在x 轴方向也将发生线位移 但在小变形情况下,梁的挠度远小于跨长,梁变形后的轴线是一条平坦的曲线横截面形心沿x 轴方向的线位移与挠度相比属于高阶微量,可略去不记因此在选定坐标后,梁变形后的轴线可表达为()f x ω=式中,x 为梁在变形前轴线上任一点的横坐标;ω为该点的挠度梁变形后的轴线称为挠曲线,在线弹性范围内,也称为弹性曲线上述表达式则称为挠曲线(或弹性曲线)方程由于挠曲线为一平坦曲线,故转角θ可表达为''tan ()f x θθω≈== 称为转角方程即挠曲线上任一点处的切线斜率'ω可足够精确地代表该点处横截面的转角θ 由此可见,求得挠曲线方程后,就能确定梁任一横截面挠度的大小,指向及转角的数值 正值的挠度向下,负值的挠度向上正值的转角为逆时针转向,负值的转角为顺时针方向2.梁的挠曲线近似微分方程及其积分为求得梁的挠曲线方程,利用曲率κ与弯矩M 间的物理关系,即 1M EIκρ== 式中曲率κ为度量挠曲线弯曲程度的量,是非负的这是梁在线弹性范围内纯弯曲情况下的曲率表达式在横力弯曲时,梁横截面上除弯矩M 外尚有剪力S F 但工程用梁,其跨长l 一般均大于横截面高度的10倍剪力S F 对于梁位移的影响很小,可略去不计,故该式子依然适用式中的M 和ρ均为x 的函数,即1()()()M x x x EIκρ== 在数学中,平面曲线的曲率与曲线方程导数间的关系有'''23/21()(1)x ωρω=±+ 取x 轴向右为正,y 轴向下为正时曲线凸向上时''ω为正,凸向下时为负而按弯矩的正、负号规定,梁弯曲后凸向下时为正,凸向上为负,符号相反于是得到 '''23/2()(1)M x EIωω=-+ 由于梁的挠曲线为一平坦曲线,因此,'2ω与1相比十分微小可以略去不计故上式可近似的写为 ''()M x EIω=-上式略去了剪力S F 的影响,并略去了'2ω项 故称为梁的挠曲线近似微分方程若为等截面直梁,其弯曲刚度EI 为一常量,上式可改写为''()EI M x ω=-对于等直梁,上式进行积分,并通过由梁的变形相容条件给出的边界条件确定积分常数 即可求得梁的挠曲线方程当全梁各横截面上的弯矩可用单一的弯矩方程表示时,梁的挠曲线近似微分方程仅有一个 将上式的两端各乘以dx ,经积分一次,得'1()EI M x dx C ω=-+⎰再积分一次,即得12[()]EI M x dx dx C x C ω=-++⎰两式子中积分常数1C 、2C 可通过挠曲线的边界条件确定例如在简支梁中,左右铰支座处的挠度均等于零在悬臂梁中,固定端处的挠度和转角均等于零确定积分常数1C 、2C 后,就分别得到梁的转角方程和挠曲线方程从而可以确定任一横截面的转角和挠度1C 和2C 的几何意义 由于以x 为自变量,在坐标原点即0x =处的定积分恒等于零因此,积分常数'100x C EI EI ωθ===,20C EI ω=式中,0θ和0ω分别表示坐标原点处截面的转角和挠度若梁上的荷载不连续即分布荷载在跨度中间的某点处开始或结束,以及集中荷载或集中力偶作用处梁的弯矩需分段写出,各段梁的挠曲线近似微分方程也随之不同在对各段梁的近似微分方程积分时,均将出现两个积分常数为确定这些积分常数,除需利用支座处的约束条件外还需利用相邻两段梁在交界处位移的连续条件例如左、右两段梁在交界处的截面应具有相等的挠度和转角不论是约束条件和连续条件,均发生在各段挠曲线的边界处故均成为边界条件,即弯曲位移中的变形相容条件遵循两个原则①对各段梁,都是从同一坐标原点到截面之间的梁段上的外力列出弯矩方程所以后一段梁的弯矩方程包括前一段的弯矩方程的新增的()x a -项②对()x a -项的积分,以()x a -作为自变量于是由x a =处的连续条件,就能得到两段梁上相应的积分常数分别相等的结果 对于弯矩方程需分为任意几段的情况,只要遵循上述规则同样可以得到各梁段上相应的积分常数分别相等的结果从而简化确定积分常数的运算3.按叠加原理计算梁的挠度和转角梁在微小变形条件下,其弯矩与荷载成线性关系 在线弹性范围内,挠曲线的曲率与弯矩成正比当挠度很小时,曲率与挠度间呈线性关系梁的挠度和转角均与作用在梁上的荷载成线性关系在这种情况下梁在几项荷载(如集中力、集中力偶或分布力)同时作用下某一横截面的挠度或转角 就分别等于每项荷载单独作用下该截面的挠度或转角的叠加,即为叠加原理 已知梁在每项荷载单独作用下的挠度和转角表则按叠加原理来计算梁的最大挠度和最大转角将较为方便4.奇异函数·梁挠曲线的初参数方程5.梁的刚度校核·提高梁的刚度的措施5.1 梁的刚度校核对于梁的挠度,其许可值通常用许可挠度与跨长之比值[]l ω作为标准 梁的刚度条件可表达为 max[]ll ωω≤ max []θθ≤ 一般土建工程中的构件,强度要求是主要的刚度要求一般处于从属地位但当对构件的位移限制很严,或按强度条件所选用的构件截面过于单薄时刚度条件也可能起控制作用5.2 提高梁的刚度的措施由梁的位移表可见梁的位移(挠度和转角)除了与梁的支承和荷载情况有关还与其弯曲刚度EI 成反比,与跨长l 的n 次幂成正比减小梁的位移,可采取下列措施①增大梁的弯曲刚度EI②调整跨长和改变结构5.梁内的弯曲应变能当梁弯曲时,梁内将积蓄应变能梁在线弹性变形过程中弯曲应变能V ε在数值上等于作用在梁上的外力所作的功W梁在纯弯曲时各横截面上的弯矩M 为常数,并等于外力偶矩e M当梁处于线弹性范围内e EI EI θρ=== θ与e M 呈线性关系直线下的三角形面积就代表外力偶所作的功W ,即12e W M θ=从而得纯弯曲时梁的弯曲应变能 12e V M εθ=即得2222e M l M l V EI EIε== 横力弯曲时,梁内应变能包含两个部分:与弯曲变形相应的弯曲应变能和与切应变形相应的剪切应变能对于弯曲应变能,取长为dx 的梁段,其相邻两横截面的弯矩应分别为()M x 和()()M x dM x +在计算微段的应变能时,弯矩的增量为一阶无穷小,可略去不计 计算器弯曲应变能为2()2M x dV dx EIε= 全梁的弯曲应变能则可通过积分求得为2()2l M x V dx EIε=⎰ 式中,()M x 为梁任一横截面上的弯矩表达式 当各段梁的弯矩表达式不同时,积分需分段进行梁的剪切应变能远小于弯曲应变能,可略去不计。