5-3 角动量相加
- 格式:pdf
- 大小:1.03 MB
- 文档页数:18


角动量公式大全
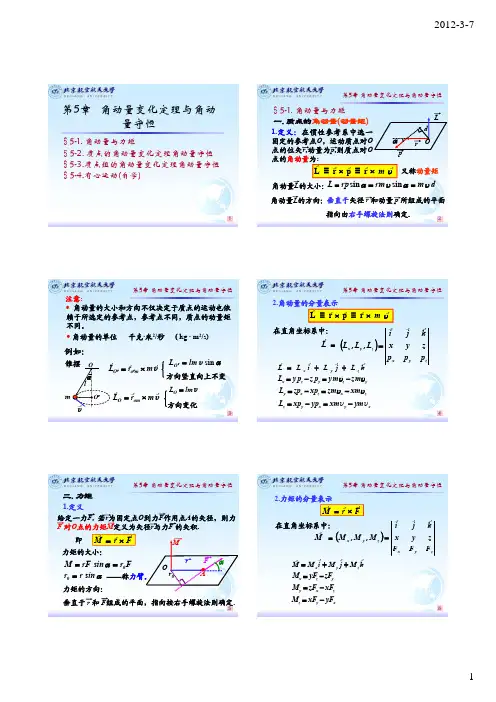
1. 质点的角动量。
- 对于质点,角动量→L=→r×→p,其中→r是质点相对于参考点的位置矢量,→p = m→v是质点的动量(m为质点质量,→v为质点的速度)。
- 在直角坐标系下,如果→r=(x,y,z),→p=(p_x,p_y,p_z),则L_x = yp_z -
zp_y,L_y=zp_x - xp_z,L_z = xp_y - yp_x。
2. 刚体定轴转动的角动量。
- 对于刚体绕定轴转动,角动量L = Iω,其中I是刚体对该轴的转动惯量,ω是刚体绕轴转动的角速度。
- 对于由多个质点组成的刚体,I=∑_im_ir_i^2(离散质点情况),对于质量连续分布的刚体,I=∫ r^2dm,这里r是质点到转动轴的垂直距离。
3. 角动量定理相关公式。
- 角动量定理→M=(d→L)/(dt),其中→M是合外力矩。
- 在刚体定轴转动中,M = Iα(α为角加速度),这是由M=(dL)/(dt)(L =
Iω)推导而来,因为(dL)/(dt)=I(dω)/(dt)=Iα。
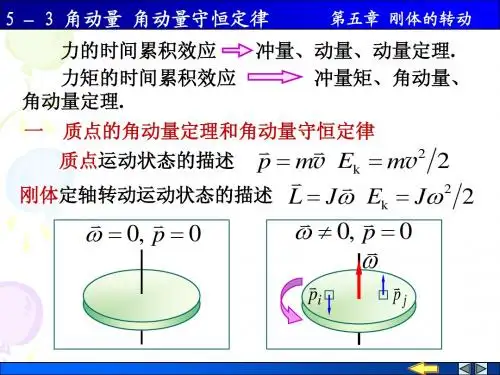
4. 角动量守恒定律。
- 当→M=0时,→L=常量。
- 在刚体定轴转动中,如果合外力矩为零,则Iω=常量,例如在花样滑冰运动员旋转时,收缩手臂(I减小),则ω增大以保持角动量守恒。

第五章角动量角动量守恒定理本章结构框图学习指导本章概念和内容是中学没有接触过的,是大学物理教学的重点和难点。
许多同学容易将平动问题与转动问题中的概念和规律混淆,例如两种冲击摆问题。
建议采用类比方法,对质量与转动惯量、动量与角动量、力与力矩、冲量与角冲量、平动动能和转动动能、运动学的线量和角量、动量定理和角动量定理、动量守恒和角动量守恒……一一加以比较。
本章的重点是刚体定轴转动问题,注意定轴条件下,各种规律都应该用标量式表示。
还请注意动量守恒在天体问题、粒子问题中的应用。
基本要求1.理解质点、质点系、定轴刚体的角动量概念。
2.理解定轴刚体的转动惯量概念,会进行简单计算。
3.理解力矩的物理意义, 会进行简单计算。
4.掌握刚体定轴转动定律,熟练进行有关计算。
5.理解角冲量(冲量矩)概念,掌握质点、质点系、定轴刚体的角动量定理,熟练进行有关计算。
6.掌握角动量守恒的条件,熟练应用角动量守恒定律求解有关问题。
内容提要1.基本概念刚体对定轴的转动惯量:是描述刚体绕定轴转动时,其转动惯性大小的物理量。
定义为刚体上每个质元(质点、线元、面元、体积元)的质量与该质元到转轴距离平方之积的总和。
即:I的大小与刚体总质量、质量分布及转轴位置有关。
质点、质点系、定轴刚体的角动量:角动量也称动量矩,它量度物体的转动运动量,描述物体绕参考点(轴)旋转倾向的强弱。
表5.1对质点、质点系、定轴刚体的角动量进行了比较。
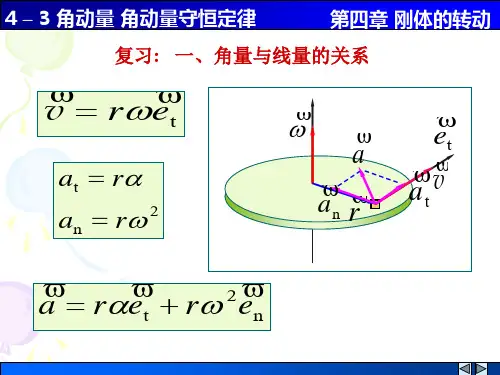
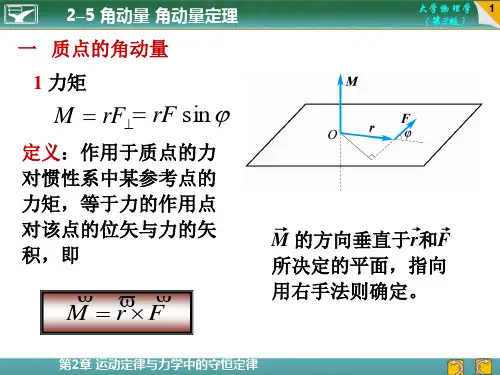
表5.1质点、质点系和定轴刚体的角动量力矩:力的作用点对参考点的位矢与力的矢积叫做力对该参考点的力矩(图5.1):即:大小:(力×力臂)方向:垂直于决定的平面,其指向由右手定则确定。
对于力矩的概念应该注意明确以下问题:•区分力对参考点的力矩和力对定轴的力矩:力对某轴的力矩是力对轴上任意一点的力矩在该轴上的投影。
例如:某力对x、y、z轴的力矩就是该力对原点的力矩在三个坐标轴上的投影:由上可知:力对参考点的力矩是矢量,而力对定轴的力矩是代数量。




相关公式大全角动量角动量相关公式大集合。
今天咱们来唠唠角动量这个超有趣的东西,还有那些和它相关的公式哦。
一、角动量的基本概念。
角动量啊,就像是物体旋转时的一种“旋转动量”。
想象一下,一个旋转的陀螺,它就有着自己的角动量呢。
从物理学的角度来说,对于一个质点,角动量L等于质点的位置矢量r和它的动量p的叉乘,也就是L = r × p。
这里的位置矢量r呢,就是描述质点相对于某个参考点的位置的矢量,动量p大家应该比较熟悉啦,就是质量m乘以速度v哦。
这个公式就是角动量最最基本的定义式啦。
就好像是给角动量这个概念找到了它在数学世界里的身份证一样呢。
二、刚体的角动量。
要是说到刚体的角动量,那又有点不一样啦。
对于一个绕着固定轴转动的刚体,它的角动量L等于转动惯量I乘以角速度ω。
这里的转动惯量I就像是刚体对于转动的一种“惯性”的度量。
比如说,一个大圆盘和一个小圆盘,如果让它们以同样的角速度转动,大圆盘因为质量分布比较分散,它的转动惯量就会比较大,相应的角动量也会比较大哦。
这个公式L = Iω就像是刚体转动世界里的一个宝藏公式,能帮我们解决好多关于刚体转动时角动量的问题呢。
三、角动量守恒定律。
这可是个超级重要的定律哦。
当一个系统所受的合外力矩为零的时候,这个系统的角动量就守恒。
比如说,一个花样滑冰运动员在冰面上旋转的时候,她把手臂收起来的时候就会转得更快,这是为啥呢?因为她这个系统(把她自己看作一个系统哦)几乎不受外力矩的作用,当她把手臂收起来的时候,她的转动惯量I变小了,根据角动量守恒定律L = Iω(这里的L是守恒不变的),那角速度ω就会变大,所以她就转得更快啦。
这就像是一个神奇的魔法,通过改变自己的形状就能改变自己的转动速度呢。
四、角动量在不同坐标系下的表达式。
在不同的坐标系下,角动量的表达式也会有一些变化哦。
在直角坐标系中,角动量有它的x、y、z分量的表达式。
Lx = ypz - zpy,Ly = zpx - xpz,Lz = xpy - ypx。