初中数学中考试题集锦圆相关试题大全

初三数学圆测试题及答案一、选择题（每题3分，共30分）1. 下列说法正确的是（）。

A. 圆的直径是半径的2倍B. 圆的周长是直径的π倍C. 圆的面积是半径的平方乘以πD. 圆的周长是半径的2π倍答案：D2. 圆的面积公式为（）。

A. S = πrB. S = πr²C. S = πdD. S = πd²答案：B3. 圆的周长公式为（）。

A. C = 2πrB. C = 2πdC. C = πrD. C = πd答案：A4. 圆心角为60°的扇形面积是（）。

A. πr²/6B. πr²/3C. πr²/2D. πr²答案：A5. 一个圆的半径为3cm，其面积为（）。

A. 9π cm²B. 18π cm²C. 27π cm²D. 36π cm²答案：C6. 圆的直径增加1倍，其面积增加（）。

A. 1倍B. 2倍C. 4倍D. 8倍答案：C7. 圆的半径增加1倍，其周长增加（）。

A. 1倍B. 2倍C. 3倍D. 4倍答案：B8. 一个圆的周长为12.56cm，其直径为（）。

A. 2cmB. 4cmC. 6cmD. 8cm答案：B9. 圆的半径为4cm，其直径为（）。

A. 2cmB. 4cmC. 8cmD. 16cm答案：C10. 圆的半径为2cm，其周长为（）。

A. 4π cmB. 8π cmC. 12π cmD. 16π cm答案：B二、填空题（每题3分，共30分）1. 圆的周长公式为______。

答案：C = 2πr2. 圆的面积公式为______。

答案：S = πr²3. 圆的直径是半径的______倍。

答案：24. 圆的周长是直径的______倍。

答案：π5. 圆的面积是半径的平方乘以______。

答案：π6. 圆心角为90°的扇形面积是圆面积的______。

答案：1/47. 圆心角为180°的扇形面积是圆面积的______。

中考数学圆经典必考题型中考试题（附答案）解答题1.（已知：如图，△ ABC 内接于O O 过点B 作的切线，交 CA 的延长线于点 E / EB & 2① 求证：AB= AC1AB ② 若tan / ABE=丄，（i ）求 的值；（ii ）求当 AC= 2时，AE 的长. 2BC=4cm 求O o 的半径.2.如图,PA 为O O 的切线, A 为切点，O 0的割线PBC 过点0与O O 分别交于B 、C, PA= 8cm PB3.已知：如图，BC 是O 0的直径，AC 切O 0于点C AB 交O 0于点D,若AD ： DB= 2 : 3, AC= 10,求 sin B 的值.4.如图，PC 为O 0的切线，C 为切点，PAB 是过0的割线,1若tan B= _ , PC= 10cm 求三角形BCD的面积.25•如图，在两个半圆中，大圆的弦MNW小圆相切，D为切点，且MN AB MN a, ON CD分别为两圆的半径，求阴影部分的面积.6.已知，如图，以△ ABC的边AB作直径的O O分别并AC BC于点D E,弦FG// AB S A CDE S△ ABC= 1 : 4, DE= 5cm FG= 8cm,求梯形AFG啲面积.7.如图所示：PA为O O的切线，A为切点，PBC是过点O的割线,PA= 10, PB= 5，求：(1)O O的面积(注：用含n的式子表示)；(2)cos / BAP的值.参考答案1.( 1)v BE 切O O 于点 B ,「. / ABE=Z C./ EBC= 2/ C,即 / ABH / ABC= 2/C,/ C +Z ABO 2 / C,/ ABC=Z C, ••• AB= AC.(2)①连结AO 交BC 于点F ,AB- AC, AOL BC 且 BF = FC.AF 在 Rt A ABF 中， =tan / ABF BF1 又 tan / ABF= tan C = tan / ABE=2 AF = 1 BF.AB AB .5BC 2BF4 ②在△ EBA M^ ECB 中 ,^EA 2- EA- (EA^ AC ),又 EA M 0 , 5 11EA= AC EA= — x 2 = 10 .5 11 11 22 •设O 的半径为r ,由切割线定理，得 PA = PB- PCAC 切O O 于点C,线段ADB 为O O 的割线,2AC = AD- ABAB= AM DB= 2k + 3k = 5k ,2 210 = 2k X 5k,••• k = 10,AB= AF 2 * * * BF 2BF 2 AF = 1BF 2/ E =Z E , / EBA=Z ECB△ EBA^A ECBEAEBBE 2 AB BC ,解之，得 EA ECk> 0,「. k= 10 .AB= 5k= 10 .AC切O O于C, BC为O O的直径,ACL BC在Rt A ACB中, sin B=虫10 10 .AB 5 屁5CD L AB于点D,/ADC=Z BD= 90°,/ 2= 90°—/ BAC=Z B.1tan B=2tan / 2=—.2AD CD 1 ACCD DB 2 CB .设AD= x (x > 0), CD= 2x, DB= 4x, AB= 5x .•/ PC切O O于点C,点B在O O上，• / 1 = / B./ P=/ P,「. △ PAC^ PCBPA AC 1PC CB 2 .PC= 10,「. PA= 5,PC 切O O 于点C, PAB 是O 0的割线,2PC = PA- PB210 = 5 (5 + 5 x ).解得 x = 3.AD= 3, CD= 6, DB= 12.1 1S ^BCD = CD" DB= — x 6X 12 = 36.2 22即三角形BCD 的面积36cm .PA= 10,二 PB= 20.2由切割线定理，得 PC = PA- PBA 內 DB= x + 4x = 15,解得 x = 3,CD= 2x = 6, DB= 4x = 12.S A BCD = ^CD- DB= 1 x 6X 12= 36.2 22即三角形BCD 的面积36cm .5.解：如图取 MN 的中点E 连结OE解法二：同解法一，由△ PAC^A PCB 得 PA PC AC CBPB 101220 AB= PB- PA= 15,2 2 2 a在 Rt A NOE 中 NO- OE = EN =2 6.解：T / CDE=/ CBA / DCE=/ BCA /• △ CDE^A ABC2S CDEDE S ABC AB DE = S CDE =任=1AB S ABC ' 42 ' 51 即 ，解得 AB= 10 (cm ,AB 2作OML FG 垂足为M11 则 FM= ^FG=丄^ 8= 4 (cm),22连结OF 11 OA= AB= — x 10= 5 (cm ).2 2OF= OA= 5 (cm ).在Rt A OMF 中由勾股定理，得 OM = . OF 2 FM 2 = -52 42 = 3 (cm ).A B FG10 Q 2 ••• 梯形 AFG 啲面积= -------------- • OM= -------- x 3 = 27 (cm ).2 27. 2 1 a n2 n ・ — =—a 2 2 8 2 2 1n( NO — OE ) 2 （平方单位）. (2) CBAP AC PA △ ACP^A BAP —— P P AB PBAC 2AB 1S阴影 ⑴PA 是。

中考数学关于圆的22道经典题1、如图，⊙O 的半径等于1，弦AB 和半径OC 互相平分于点M.求扇形OACB 的面积（结果保留π）解：∵弦AB 和半径OC 互相平分∴OC ⊥ABOM=MC=21OC=21OA 在Rt △OAM 中，sinA=21=OA OM ∴∠A=30°又∵OA=OB ∴∠B=∠A=30° ∴∠AOB=120° ∴S 扇形＝33601120ππ=⋅⋅2、如图，△ABC 内接于⊙O ，AB ＝6,AC ＝4,D 是AB 边上一点，P 是优弧BAC 的中点，连结PA 、PB 、PC 、PD.(1)当BD 的长度为多少时，△PAD 是以AD 为底边的等腰三角形？并证明； （2）若cos ∠PCB=55，求PA 的长. 解：（1）当BD ＝AC ＝4时，△PAD 是以AD 为底边的等腰三角形 ∵P 是优弧BAC 的中点 ∴弧PB ＝弧PC ∴PB ＝PC∵BD ＝AC ＝4 ∠PBD=∠PCA ∴△PBD ≌△PCA∴PA=PD 即△PAD 是以AD 为底边的等腰三角形（2）由（1）可知，当BD ＝4时，PD ＝PA ，AD ＝AB-BD ＝6-4＝2过点P 作PE ⊥AD 于E ，则AE ＝21AD=1 ∵∠PCB=∠PAD ∴cos ∠PAD=cos ∠PCB=55=PA AE ∴PA=53、如图，AB 是⊙O 的直径，C 是的中点，CE ⊥AB 于 E ，BD 交CE 于点F ．（1）求证：CF ﹦BF ；（2）若CD ﹦6， AC ﹦8，则⊙O 的半径为 ▲ ，CE 的长是 ▲ ．CBDEFO 12解：(1) 证明：∵AB 是⊙O 的直径，∴∠ACB ﹦90° 又∵CE ⊥AB ， ∴∠CEB ﹦90° ∴∠2﹦90°－∠A ﹦∠1又∵C 是弧BD 的中点，∴∠1﹦∠A ∴∠1﹦∠2,∴ CF ﹦BF ﹒ …………………4分 (2) ⊙O 的半径为5 ， CE 的长是524﹒ ………4分（各2分）4、已知：AB 是⊙O 的弦，D 是AB 的中点，过B 作AB 的垂线交AD 的延长线于C ． （1）求证：AD ＝DC ；（2）过D 作⊙O 的切线交BC 于E ，若DE ＝EC ，求sin C ．证明：连BD ∵BD AD =∴∠A ＝∠ABD ∴AD ＝BD …………………2分 ∵∠A +∠C ＝90°，∠DBA +∠DBC ＝90°∴∠C ＝∠DBC ∴BD ＝DC∴AD ＝DC ………………………………………………………4分 （2）连接OD ∵DE 为⊙O 切线 ∴OD ⊥DE …………………………5分 ∵BD AD =，OD 过圆心 ∴OD ⊥AB又∵AB ⊥BC ∴四边形FBED 为矩形∴DE ⊥BC ……………………6分 ∵BD 为Rt △ABC 斜边上的中线∴BD ＝DC ∴BE ＝EC ＝DE∴∠C ＝45° …………………………………………………7分 ∴sin ∠C =22………………………………………………………………8分5、如图，AB 是O 的直径，C 为圆周上一点，30ABC ∠=︒，O 过点B 的切线与CO 的延长线交于点D ．求证：（1）CAB BOD ∠=∠；（2）ABC ∆≌ODB ∆． （1）∵AB 是O 的直径，∴90ACB ∠=︒，由30ABC ∠=︒，∴60CAB ∠=︒BE CDAOO A D B ECDCBOA又OB OC =，∴30OCB OBC ∠=∠=︒∴60BOD ∠=︒，∴CAB BOD ∠=∠．…… 4分（2）在Rt ABC ∆中，30ABC ∠=︒，得12AC AB =，又12OB AB =，∴AC OB =． 由BD 切O 于点B ，得90OBD ∠=︒．在ABC ∆和ODB ∆中，CAB BODACB OBD AC OB ∠=∠∠=∠⎧=⎪⎨⎪⎩∴ABC ∆≌ ODB ∆ …… 8分6、如图，⊙O 的半径等于1，弦AB 和半径OC 互相平分于点M.求扇形OACB 的面积（结果保留π）解：∵弦AB 和半径OC 互相平分∴OC ⊥ABOM=MC=21OC=21OA 在Rt △OAM 中，sinA=21=OA OM ∴∠A=30°又∵OA=OB ∴∠B=∠A=30° ∴∠AOB=120° ∴S 扇形＝33601120ππ=⋅⋅7、如图，在矩形ABCD 中，点O 在对角线AC 上，以OA 的长为半径的圆O 与AD 、AC 分别交于点E 、F ，且∠ACB=∠DCE ．(1)判断直线CE 与⊙O 的位置关系，并证明你的结论；(2)若tan ∠ACB=22，BC=2，求⊙O 的半径．答案：1）直线CE 与⊙O 相切。

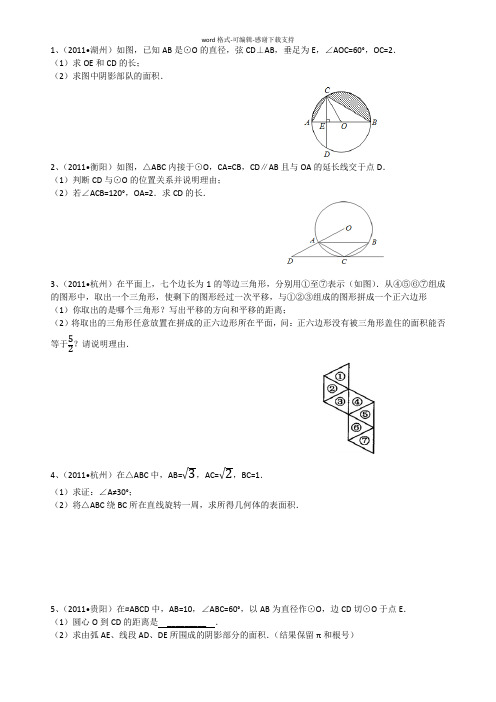
1、（2011•湖州）如图，已知AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，∠AOC=60°，OC=2．（1）求OE 和CD 的长；（2）求图中阴影部队的面积．2、（2011•衡阳）如图，△ABC 内接于⊙O ，CA=CB ，CD ∥AB 且与OA 的延长线交于点D ．（1）判断CD 与⊙O 的位置关系并说明理由；（2）若∠ACB=120°，OA=2．求CD 的长．3、（2011•杭州）在平面上，七个边长为1的等边三角形，分别用①至⑦表示（如图）．从④⑤⑥⑦组成的图形中，取出一个三角形，使剩下的图形经过一次平移，与①②③组成的图形拼成一个正六边形（1）你取出的是哪个三角形？写出平移的方向和平移的距离；（2）将取出的三角形任意放置在拼成的正六边形所在平面，问：正六边形没有被三角形盖住的面积能否等于52？请说明理由．4、（2011•杭州）在△ABC 中，AB=√3，AC=√2，BC=1． （1）求证：∠A≠30°；（2）将△ABC 绕BC 所在直线旋转一周，求所得几何体的表面积．5、（2011•贵阳）在▱ABCD 中，AB=10，∠ABC=60°，以AB 为直径作⊙O ，边CD 切⊙O 于点E ．（1）圆心O 到CD 的距离是 _________ ．（2）求由弧AE 、线段AD 、DE 所围成的阴影部分的面积．（结果保留π和根号）6、（2011•抚顺）如图，AB 为⊙O 的直径，弦CD 垂直平分OB 于点E ，点F 在AB 延长线上，∠AFC=30°．（1）求证：CF 为⊙O 的切线．（2）若半径ON ⊥AD 于点M ，CE=√3，求图中阴影部分的面积．7、（2011•北京）如图，在△ABC ，AB=AC ，以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ，点F 在AC 的延长线上，且∠CBF=12∠CAB ．（1）求证：直线BF 是⊙O 的切线；（2）若AB=5，sin ∠CBF=√55，求BC 和BF 的长．8、（2010•义乌市）如图，以线段AB 为直径的⊙O 交线段AC 于点E ，点M 是AE ̂的中点，OM 交AC 于点D ，∠BOE=60°，cosC=12，BC=2√3．（1）求∠A 的度数；（2）求证：BC 是⊙O 的切线 （3）求MD 的长度．9、（2010•沈阳）如图，AB 是⊙O 的直径，点C 在BA 的延长线上，直线CD 与⊙O 相切与点D ，弦DF ⊥AB 于点E ，线段CD=10，连接BD ．（1）求证：∠CDE=2∠B ；（2）若BD ：AB=√3：2，求⊙O 的半径及DF 的长．10、（2010•绍兴）如图，已知△ABC 内接于⊙O ，AC 是⊙O 的直径，D 是AB ̂的中点，过点D 作直线BC的垂线，分别交CB 、CA 的延长线E 、F ．（1）求证：EF 是⊙O 的切线；（2）若EF=8，EC=6，求⊙O 的半径．11、（2010•丽水）如图，直线l 与⊙O 相交于A ，B 两点，且与半径OC 垂直，垂足为H ，已知AB=16cm ，．（1）求⊙O 的半径；（2）如果要将直线l 向下平移到与⊙O 相切的位置，平移的距离应是多少？请说明理由．1、（2011•湖州）如图，已知AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，∠AOC=60°，OC=2．（1）求OE 和CD 的长；（2）求图中阴影部队的面积．考点：扇形面积的计算；垂径定理。

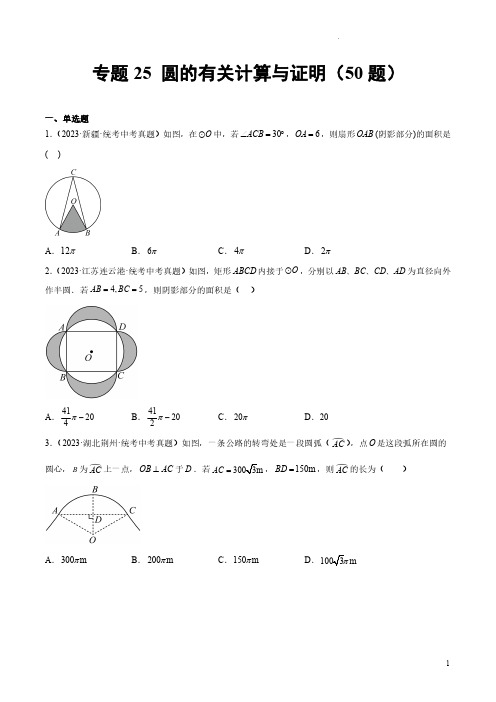
专题25圆的有关计算与证明（50题）一、单选题1．（2023·新疆·统考中考真题）如图，在O 中，若30ACB ∠=︒，6OA =，则扇形OAB (阴影部分)的面积是()A ．12πB ．6πC ．4πD ．2π2．（2023·江苏连云港·统考中考真题）如图，矩形ABCD 内接于O ，分别以AB BC CD AD 、、、为直径向外作半圆．若4,5==AB BC ，则阴影部分的面积是（）A ．41204π-B ．41202π-C ．20πD ．203．（2023·湖北荆州·统考中考真题）如图，一条公路的转弯处是一段圆弧（ AC ），点O 是这段弧所在圆的圆心，B 为 AC 上一点，OB AC ⊥于D ．若3003m AC =，150m BD =，则 AC 的长为（）A ．300m πB ．200m πC ．150m πD ．1003mπA ．21cm 4πB 5．（2023·四川达州·统考中考真题）如图，四边形段90︒的圆心角的圆心为为A BCD 、、、循环，则A ．40452πB ．20236．（2023·四川广安·统考中考真题）如图，在等腰直角心，AC 为半径画弧，交AB 于点积是（）A ．π2-B ．2π2-7．（2023·江苏苏州·统考中考真题）如图，AB 是半圆O 的直径，点,C D 在半圆上， CDDB =，连接,,OC CA OD ，过点B 作EB AB ⊥，交OD 的延长线于点E ．设OAC 的面积为1,S OBE △的面积为2S ，若1223S S =，则tan ACO ∠的值为（）A ．2B ．223C ．75D ．32二、填空题8．（2023·重庆·统考中考真题）如图，在矩形ABCD 中，2AB =，4BC =，E 为BC 的中点，连接AE DE ，，以E 为圆心，EB 长为半径画弧，分别与AE DE ，交于点M ，N ，则图中阴影部分的面积为________．（结果保留π）9．（2023·黑龙江绥化·统考中考真题）如图，O 的半径为2cm ，AB 为O 的弦，点C 为 AB 上的一点，将 AB 沿弦AB 翻折，使点C 与圆心O 重合，则阴影部分的面积为_______．（结果保留π与根号）10．（2023·重庆·统考中考真题）如图，O 是矩形ABCD 的外接圆，若4,3AB AD ==，则图中阴影部分的面积为___________．（结果保留π）14．（2023·天津·统考中考真题）如图，在每个小正方形的边长为且顶点A，B均在格点上．（1）线段AB的长为________（2）若点D在圆上，AB与CD为等边三角形，并简要说明点15．（2023·江苏苏州·统考中考真题）如图，在H AH=．以点A为圆心，,3一个圆锥的侧面，记这个圆锥底面圆的半径为r r-=________________的半径为2r，则1216．（2023·四川自贡·统考中考真题）如图，小珍同学用半径为8cm ，圆心角为100︒的扇形纸片，制作一个底面半径为2cm 的圆锥侧面，则圆锥上粘贴部分的面积是________2cm ．三、解答题17．（2023·四川南充·统考中考真题）如图，AB 与O 相切于点A ，半径OC AB ∥，BC 与O 相交于点D ，连接AD ．(1)求证：OCA ADC ∠∠=；(2)若12,tan 3AD B ==，求OC 的长．18．（2023·四川成都·统考中考真题）如图，以ABC 的边AC 为直径作O ，交BC 边于点D ，过点C 作CE AB ∥交O 于点E ，连接AD DE ，，B ADE ∠=∠．(1)求证：AC BC =；(2)若tan 23B CD ==，，求AB 和DE 的长．(1)求证：90ADC BAC ∠-∠=︒；（请用两种证法解答）(2)若ACP ADC ∠=∠，O 的半径为3，4CP =，求AP 的长．(1)求BED ∠的度数；(2)如图2，过点A 作O 的切线交BC 延长线于点F ，过点D 作DG 235,4AD DE ==，求DG 的长．21．（2023·浙江杭州·统考中考真题）在边长为1的正方形ABCD 中，点射线BE 与射线CD 交于点F ．(1)若13ED =，求DF 的长．(2)求证：1AE CF ⋅=．(3)以点B 为圆心，BC 长为半径画弧，交线段BE 于点G ．若EG ED =，求ED 的长．22．（2023·河北·统考中考真题）装有水的水槽放置在水平台面上，其横截面是以AB 为直径的半圆O ，50cm AB =，如图1和图2所示，MN 为水面截线，GH 为台面截线，MN GH ∥．计算：在图1中，已知48cm MN =，作OC MN ⊥于点C ．（1）求OC 的长．操作：将图1中的水面沿GH 向右作无滑动的滚动，使水流出一部分，当30ANM ∠=︒时停止滚动，如图2．其中，半圆的中点为Q ，GH 与半圆的切点为E ，连接OE 交MN 于点D ．探究：在图2中(1)求证：2AOB ∠=∠(2)若4,5AB BC ==径，45ABD ∠=︒，直线l 与三条线段CD 、CA 、DA 的延长线分别交于点E 、F 、G ．且满足45CFE ∠=︒．(1)求证：直线l ⊥直线CE ；(2)若AB DG =；①求证：ABC GDE △≌△；②若312R CE ==，，求四边形ABCD 的周长．25．（2023·天津·统考中考真题）在O 中，半径OC 垂直于弦AB ，垂足为D ，60AOC ∠=︒，E 为弦AB 所对的优弧上一点．(1)如图①，求AOB ∠和CEB ∠的大小；(2)如图②，CE 与AB 相交于点F ，EF EB =，过点E 作O 的切线，与CO 的延长线相交于点G ，若3OA =，求EG 的长．26．（2023·江苏苏州·统考中考真题）如图，ABC 是O 的内接三角形，AB 是O 的直径，5,25AC BC ==，点F 在AB 上，连接CF 并延长，交O 于点D ，连接BD ，作BE CD ⊥，垂足为E ．(1)求证：DBE ABC △∽△；(2)若2AF =，求ED 的长．27．（2023·四川达州·统考中考真题）如图，ABC ABD 、内接于O AB BC P = ，，是OB 延长线上的一点，PAB ACB ∠=∠，AC BD 、相交于点E ．(1)求证：AP 是O 的切线；(2)若24BE DE ==，，30P ∠=︒，求AP 的长．28．（2023·湖南·统考中考真题）如图，AB 是O 的直径，AC 是一条弦，D 是 AC 的中点，DE AB ⊥于点E ，交AC 于点F ，交O 于点H ，DB 交AC 于点G ．(1)求证：AF DF =．(2)若55,sin 25AF ABD =∠=，求O 的半径．29．（2023·湖南怀化·统考中考真题）如图，AB 是O 的直径，点P 是O 外一点，PA 与O 相切于点A ，点C 为O 上的一点．连接PC 、AC 、OC ，且PC PA =．(1)求证：PC 为O 的切线；(2)延长PC 与AB 的延长线交于点D ，求证：PD OC PA OD ⋅=⋅；(3)若308CAB OD ∠=︒=，，求阴影部分的面积．30．（2023·四川眉山·统考中考真题）如图，ABC 中，以AB 为直径的O 交BC 于点E ．AE 平分BAC ∠，过点E 作ED AC ⊥于点D ，延长DE 交AB 的延长线于点P ．(1)求证：PE 是O 的切线；(2)若1sin ,43P BP ∠==，求CD 的长．31．（2023·安徽·统考中考真题）已知四边形(1)如图1，连接,OA CA ，若OA BD ⊥，求证；CA 平分BCD ∠；(2)如图2，E 为O 内一点，满足,AE BC CE AB ⊥⊥，若BD =32．（2023·吉林长春·统考中考真题）【感知】如图①，点A 、B 、的大小为__________度．【探究】小明遇到这样一个问题：如图②，O 是等边三角形ABC 的外接圆，点P 在 AC 上（点P 不与点A 、C 重合），连结PA 、PB 、PC ．求证：PB PA PC =+．小明发现，延长PA 至点E ，使AE PC =，连结BE ，通过证明PBC EBA ≌△△，可推得PBE 是等边三角形，进而得证．下面是小明的部分证明过程：证明：延长PA 至点E ，使AE PC =，连结BE ，四边形ABCP 是O 的内接四边形，180BAP BCP ∴∠+∠=︒．180BAP BAE ∠+∠=︒ ，BCP BAE ∴∠=∠．ABC 是等边三角形．BA BC ∴=，(SAS)PBC EBA ∴ ≌请你补全余下的证明过程．【应用】如图③，O 是ABC 的外接圆，90ABC AB BC ∠=︒=，，点P 在O 上，且点P 与点B 在AC 的两侧，连结PA 、PB 、PC ．若22PB PA =，则PB PC的值为__________．33．（2023·四川泸州·统考中考真题）如图，AB 是O 的直径，210AB =，O 的弦CD AB ⊥于点E ，6CD =．过点C 作O 的切线交AB 的延长线于点F ，连接BC ．∠；(1)求证：BC平分DCF(2)G为 AD上一点，连接CG交AB于点H，若34．（2023·黑龙江绥化·统考中考真题）如图，行弦，弦AB交MC于点H．点A在¼MC上，点⋅=⋅．(1)求证：MH CH AH BH(2)求证：AC BC=．(3)在⊙O中，沿弦ND所在的直线作劣弧ND NG的长．35．（2023·广东·统考中考真题）综合探究如图1，在矩形ABCD中(AB>BD于点E，连接CA'．(1)求证：AA CA '⊥'；(2)以点O 为圆心，OE 为半径作圆．①如图2，O 与CD 相切，求证：3AA CA '='；②如图3，O 与CA '相切，1AD =，求O 的面积．36．（2023·山东·统考中考真题）如图，AB 为O 的直径，C 是圆上一点，D 是 BC 的中点，弦DE AB ⊥，垂足为点F ．(1)求证：BC DE =；(2)P 是»AE 上一点，6,2AC BF ==，求tan BPC ∠；(3)在（2）的条件下，当CP 是ACB ∠的平分线时，求CP 的长．37．（2023·山东·统考中考真题）如图，已知AB 是O 的直径，CD CB =，BE 切O 于点B ，过点C 作CF OE ⊥交BE 于点F ，若2EF BF =．(1)如图1，连接BD ，求证：ADB OBE △≌△；(2)如图2，N 是AD 上一点，在AB 上取一点M ，使60MCN ∠=︒，连接MN ．请问：三条线段MN BM DN ，，有怎样的数量关系？并证明你的结论．38．（2023·浙江杭州·统考中考真题）如图，在O 中，直径AB 垂直弦CD 于点E ，连接,,AC AD BC ，作CF AD ⊥于点F ，交线段OB 于点G （不与点,O B 重合），连接OF ．(1)若1BE =，求GE 的长．(2)求证：2BC BG BO =⋅．(3)若FO FG =，猜想CAD ∠的度数，并证明你的结论．39．（2023·湖北宜昌·统考中考真题）如图1，已知AB 是O 的直径，PB 是O 的切线，PA 交O 于点C ，43AB PB ==，．(1)填空：PBA ∠的度数是_________，PA 的长为_________；(2)求ABC 的面积；(3)如图2，CD AB ⊥，垂足为D ．E 是 AC 上一点，5AE EC =．延长AE ，与DC ，BP 的延长线分别交于点,F G ，求EF FG的值．40．（2023·山东滨州·统考中考真题）如图，点E 是ABC 的内心，AE 的延长线与边BC 相交于点F ，与ABC 的外接圆相交于点D ．(1)求证：::ABF ACF S S AB AC =△△；(2)求证：::AB AC BF CF =；(3)求证：2AF AB AC BF CF =⋅-⋅；(4)猜想：线段,,DF DE DA 三者之间存在的等量关系．（直接写出，不需证明．）41．（2023·浙江台州·统考中考真题）我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系，用直线上点的位置刻画圆上点的位置，如图，AB 是O 的直径，直线l 是O 的切线，B 为切点．P ，Q 是圆上两点（不与点A 重合，且在直径AB 的同侧），分别作射线AP ，AQ 交直线l 于点C ，点D ．(1)如图1，当6AB =，BP的长为π时，求BC 的长．(2)如图2，当34AQ AB =， BP PQ =时，求BC CD的值．(3)如图3，当6sin 4BAQ ∠=，BC CD =时，连接BP ，PQ ，直接写出(1)求CE 的长和y 关于x 的函数表达式．(2)当PH PN <，且长度分别等于PH ，PN ，a 的三条线段组成的三角形与(3)延长PN 交半圆O 于点Q ，当1534NQ x =-时，求43．（2023·新疆·统考中考真题）如图，AB 是O 的直径，点接AF ，过点C 作AF 的垂线，交AF 的延长线于点D 交AC 于点H ．(1)求证：CE 是O 的切线；(2)若tan 34E =，4BE =，求FH 的长．44．（2023·云南·统考中考真题）如图，BC 是O 的直径，A 是O 上异于B C 、的点．O 外的点E 在射线CB 上，直线EA 与CD 垂直，垂足为D ，且DA AC DC AB ⋅=⋅．设ABE 的面积为1,S ACD 的面积为2S ．(1)判断直线EA 与O 的位置关系，并证明你的结论；(2)若21,BC BE S mS ==，求常数m 的值．45．（2023·浙江宁波·统考中考真题）如图1，锐角ABC 内接于O ，D 为BC 的中点，连接AD 并延长交O 于点E ，连接,BE CE ，过C 作AC 的垂线交AE 于点F ，点G 在AD 上，连接,BG CG ，若BC 平分EBG ∠且BCG AFC ∠=∠．(1)求BGC ∠的度数．(2)①求证：AF BC =．②若AG DF =，求tan GBC ∠的值，(3)如图2，当点O 恰好在BG 上且1OG =时，求AC 46．（2023·四川遂宁·统考中考真题）如图，四边形D 的直线l 交BA 的延长线于点M ，交BC 的延长线于点(1)求证：MN 是O 的切线；(2)求证：2AD AB CN =⋅；(3)当6AB =，3sin 3DCA ∠=时，求AM 的长．47．（2023·四川广安·统考中考真题）如图，以Rt ABC △E 是BC 的中点，连接OE DE 、．(1)求证：DE 是O 的切线．(2)若4sin ,55C DE ==，求AD 的长．(3)求证：22DE CD OE =⋅．48．（2023·浙江嘉兴·统考中考真题）已知，AB 是半径为1的O 的弦，O 的另一条弦CD 满足CD AB =，且CD AB ⊥于点H （其中点H 在圆内，且AH BH CH DH >>，）．(1)在图1中用尺规作出弦CD 与点H （不写作法，保留作图痕迹）．(2)连结AD ，猜想，当弦AB 的长度发生变化时，线段AD 的长度是否变化？若发生变化，说明理由：若不变，求出AD 的长度；(3)如图2，延长AH 至点F ，使得HF AH =，连结CF ，HCF ∠的平分线CP 交AD 的延长线于点P ，点M 为AP 的中点，连结HM ，若12PD AD =．求证：MH CP ⊥．49．（2023·浙江·统考中考真题）如图，在O 中，AB 是一条不过圆心O 的弦，点,C D 是 AB 的三等分点，直径CE 交AB 于点F ，连结AD 交CF 于点G ，连结AC ，过点C 的切线交BA 的延长线于点H ．(1)求证：AD HC ∥；(2)若2OG GC=，求tan FAG ∠的值；(3)连结BC 交AD 于点N ，若O ①若52OF =，求BC 的长；②若10AH =，求ANB 的周长；③若88HF AB ⋅=，求BHC △的面积．50．（2023·四川宜宾·统考中考真题）如图，以CD AF ⊥交AF 的延长线于点D ，交点N ．(1)求证：CD 是O 的切线；(2)求证：EM EN =；(3)如果N 是CM 的中点，且AB =。

初中中考圆试题及答案一、选择题（每题3分，共30分）1. 圆的半径为5，直径为（）A. 10B. 5C. 15D. 202. 圆的周长公式为（）A. C=πrB. C=2πrC. C=πdD. C=2πd3. 圆的面积公式为（）A. S=πr²B. S=2πrC. S=πd²D. S=2πd4. 圆内接四边形的对角线（）A. 相等B. 不相等C. 垂直D. 平行5. 圆的切线与半径（）A. 垂直B. 相交C. 平行D. 重合6. 圆的直径是圆内最长的线段，这种说法（）A. 正确B. 错误7. 圆心到圆上任意一点的距离都相等，这种说法（）A. 正确B. 错误8. 圆的半径增加一倍，面积增加（）A. 一倍B. 两倍C. 四倍D. 八倍9. 圆的周长与直径的比值是（）A. πB. 2πC. 4πD. 1/π10. 圆的半径为3，圆的面积为（）A. 9πB. 3πC. 6πD. 12π二、填空题（每题2分，共20分）1. 圆的直径是半径的______倍。

2. 圆的周长是半径的______倍。

3. 圆的面积是半径的______倍。

4. 圆周率π的近似值是______。

5. 圆的内接三角形的内角和为______度。

6. 圆的外切三角形的外角和为______度。

7. 圆的切线与半径垂直于______。

8. 圆的切线与圆心的距离等于______。

9. 圆的直径是圆内最长的______线段。

10. 圆的半径增加一倍，面积增加______倍。

三、解答题（每题10分，共50分）1. 已知圆的半径为4，求圆的周长和面积。

2. 已知圆的直径为8，求圆的周长和面积。

3. 已知圆的周长为31.4，求圆的直径和半径。

4. 已知圆的面积为78.5，求圆的半径。

5. 已知圆的半径为5，求圆内接正六边形的边长。

答案：一、选择题1. A2. B3. A4. A5. A6. A7. A8. C9. A 10. A二、填空题1. 22. 2π3. π4. 3.145. 1806. 3607. 切点8. 半径9. 弦10. 4三、解答题1. 周长：2πr = 2 × 3.14 × 4 = 25.12；面积：πr² = 3.14 × 4² = 50.242. 周长：C = πd =3.14 × 8 = 25.12；面积：S = πr² = 3.14 × (8/2)² = 50.243. 直径：d = C/π = 31.4/3.14 = 10；半径：r = d/2 = 10/2 = 54. 半径：r = √(S/π) = √(78.5/3.14) ≈ 4.075. 边长：边长= 2r × sin(π/6) = 2 × 5 × 0.5 = 5。

初中数学中考试题集锦（圆相关试题）一、选择题： 1、（2009·浙江温州·模拟1） 图①、图②、图③是三种方法将6根钢管用钢丝捆扎的截面图，三种方法所用的钢丝长分别为, （不记接头部分），则a, b, c,的大小关系为（ ）。

A 、 >c B. C. a<b<c D. a>b>c 答案：B2、（2009·浙江温州·模拟2）如图，A 、B 是⊙O 上的两点，是⊙O 的切线，∠＝70°，则∠等于（ ） A ．20° B ．10° C ．70° D ．35° 答案：A3、（2009·浙江温州·模拟3）一个圆锥的底面半径为3㎝，它的侧面积为15π㎝2，那么这个圆锥的高线长为A 、6㎝B 、8㎝C 、4㎝D 、4π㎝ 答案：C 4、（2009·浙江温州·模拟4）如图，是的直径，，则的度数是（ ）A ．B ．C ．D ．答案：D5、（2009·浙江温州·模拟5）在半径为18的圆中，120°的圆心角所对的弧长是（ ）A ．12πB ．10πC ．6πD ．3π答案：A 6、（2009·浙江温州·模拟6）如果圆锥的母线长为6，底面圆半径为3，则这个圆锥的侧面积为（ ） A. B. C. D. 答案：B 7、（2009·浙江温州·模拟6）如图，已知⊙O 的弦、相交于点E ，的度数为60°，的度数为100°，则∠等于 （ ）（A ）60° （B ）100° （C ）80° （D ）130°答案：C 8、（2009·浙江温州·模拟7）如图，在⊙Ｏ中，弦ＡＢ，ＣＤ相交于点Ｅ。

已知∠ＥＣＢ＝６０°，图① 图②O A B C （第2题）CO第4题图∠ＡＥＤ＝６５°，那么∠ＡＤＥ的度数是（ ） Ａ. ４０° Ｂ. １５° Ｃ. ５５° Ｄ. ６５° 答案：C 9、（2009·浙江温州·模拟8）如图，已知直角坐标系中一条圆弧经过正方形网格的格点A 、B 、C 。

初三圆的试题及答案一、选择题1. 圆的半径为r，则圆的面积为（）A. πr²B. 2πrC. πrD. 4πr²答案：A2. 圆的周长公式为（）A. 2πrB. πr²C. πrD. 4πr²答案：A3. 圆的直径是半径的（）A. 1倍B. 2倍C. 3倍D. 4倍答案：B4. 圆的半径增加1倍，面积增加（）A. 1倍B. 2倍C. 3倍D. 4倍答案：D5. 圆的半径为r，圆心角为θ（弧度制），则弧长为（）A. rθB. 2πrC. πrD. 2rθ答案：A二、填空题6. 圆的半径为3cm，则圆的周长为________cm。

答案：18.84cm7. 圆的直径为10cm，则圆的面积为________cm²。

答案：78.5cm²8. 圆的周长为12.56cm，则圆的半径为________cm。

答案：2cm9. 圆的半径为5cm，圆心角为60°，则弧长为________cm。

答案：5πcm10. 圆的半径为r，圆心角为θ（弧度制），则扇形的面积为________cm²。

答案：1/2 * r² * θ cm²三、解答题11. 已知圆的半径为5cm，求圆的面积。

解：根据圆的面积公式，S = πr²，代入r = 5cm，得：S = π * 5² = 25π cm²。

12. 已知圆的周长为20πcm，求圆的半径。

解：根据圆的周长公式，C = 2πr，代入C = 20πcm，得：20π = 2πrr = 10cm。

13. 已知圆的直径为8cm，求圆的周长和面积。

解：根据圆的直径，求得半径r = 4cm。

周长C = 2πr = 2π * 4 = 8π cm。

面积S = πr² = π * 4² = 16π cm²。

14. 已知圆的半径为6cm，圆心角为90°，求弧长。

中考数学总复习《圆的综合题》专项测试卷-附参考答案一、单选题(共12题；共24分)1．已知⊙O的半径为5，点P到圆心O的距离为6，那么点P与⊙O的位置关系是A．点P在⊙O上B．点P在⊙O内C．点P在⊙O外D．无法确定2．如图，△ABC内接于⊙O，∠C=46°，连接OA，则∠OAB=（）A．44°B．45°C．54°D．67°3．下列命题：①三点确定一个圆；②相等的圆周角所对的弧相等；③平分弦的直径垂直于弦；④等弧所对的圆心角相等；其中真命题的个数是（）A．0B．1C．2D．34．若圆锥的底面半径长是5，母线长是13，则该圆锥的侧面面积是（）A．60B．60πC．65D．65π5．一块等边三角形的木板，边长为1，现将木板沿水平线翻滚（如图），那么B点从开始至结束所走过的路径长度为（）A．3π2B．4π3C．4D．2+ 3π26．下列命题正确的个数有（）①长度相等的弧叫做等弧；②三点确定一个圆；③平分弦的直径垂直于弦；④弧相等，则弧所对的圆心角相等．A．1B．2C．3D．47．如图是一个几何体的三视图，则这个几何体的侧面积是（）A．πcm2B．2 πcm2C．6πcm2D．3πcm28．如图，AB是⊙O的直径，DB、DE分别切⊙O于点B、C，若⊙ACE=25°，则⊙D的度数是（）A．50°B．55°C．60°D．65°9．如图，一条公路的转变处是一段圆弧（即图中弧CD，点O是弧CD的圆心），其中CD=600米，E 为弧CD上一点，且OE⊙CD，垂足为F，OF=300√3米，则这段弯路的长度为A．200π米B．100π米C．400π米D．300π米10．如图，⊙O的直径AB与弦CD交于点，AE=6，BE=2，CD=2 ，则⊙AED的度数是（）A．30°B．60°C．45°D．36°11．如图，AB是⊙O的直径，C，D是⊙O上的点，⊙CDB＝30°，过点C作⊙O的切线交AB的延长线于点E，则sinE的值为（）A．√32B．12C．√33D．√312．如图，⊙O的半径为3，四边形ABCD内接于⊙O，连接OB、OD，若⊙BOD=⊙BCD，则BD̂的长为（）A．πB．32πC．2πD．3π二、填空题(共6题；共7分)13．如图，△ABC中AB=2，将△ABC绕点A逆时针旋转60°得到△AB1C1，AB1恰好经过点C，则阴影部分的面积为．14．如图，Rt⊙ABC中⊙C=90°，⊙A=30°，AB=4，以AC上的一点O为圆心OA为半径作⊙O，若⊙O与边BC始终有交点（包括B、C两点），则线段AO的取值范围是．15．如图所示一张圆形光盘，已知光盘内直径为2cm，一个宽为2cm的刻度尺在圆形光盘上移动，当刻度尺的一边与光盘相切时，则另一边与光盘边缘两个交点处的读数恰好是“2”和“10”（单位：cm），那么该光盘的外直径是cm，该光盘的面积是cm2．16．如图，⊙O是△ABC的外接圆OB=√13，BC=4则tanA的值为．R，则AC 17．已知半径为R的半圆O，过直径AB上一点C，作CD⊙AB交半圆于点D，且CD=√32的长为18．如图，在矩形ABCD中AB=2，BC=4点E为BC上一动点，过点B作AE的垂线交AE于点F，连接DF则DF的最小值是．三、综合题(共6题；共60分)19．如图，在△ABC中以△ABC的边AB为直径作⊙O，交AC于点D，DE是⊙O的切线，且DE⊥BC 垂足为点E.（1）求证：AB=BC；（2）若DE=3，CE=6，求直径AB长.20．如图，AB是⊙O的直径，点C在⊙O上，AD垂直于过点C的切线，垂足为D.（1）若⊙BAD＝80°，求⊙DAC的度数；（2）如果AD＝6，AB＝8，求AC的长.21．如图，AB为⊙O的直径，点C是⊙O上的一点，AB=8cm，⊙BAC=30°，点D是弦AC上的一点.（1）若OD⊙AC，求OD长；（2）若CD=2OD，判断△ADO形状，并说明理由.22．如图，以⊙ABC的边AB为直径的⊙O与边AC相交于点D，BC是⊙O的切线，E为BC的中点，连接BD、DE．（1）求证：DE是⊙O的切线；（2）设⊙CDE的面积为S1，四边形ABED的面积为S2，若S2＝5S1，求tan⊙BAC的值．23．如图，AB、AC是⊙O的两条弦，且AB=AC，点D是弧BC的中点，连接并延长BD、CD，分别交AC、AB的延长线于点E、F.（1）求证：DF=DE（2）若BD=6，CE=8求⊙O的半径.24．如图，AB是⊙O的直径，AC是弦，D是弧BC的中点，过点D作EF垂直于直线AC,垂足为F，交AB的延长线于点E．（1）求证: EF是⊙O的切线；（2）若AF=6,EF=8，求⊙O的半径．参考答案1．【答案】C 2．【答案】A 3．【答案】B 4．【答案】D 5．【答案】B 6．【答案】A 7．【答案】A 8．【答案】A 9．【答案】A 10．【答案】C 11．【答案】B 12．【答案】C 13．【答案】23π14．【答案】√3≤OA ≤43√3 15．【答案】10；24π 16．【答案】2317．【答案】12R 或32R 18．【答案】√17−119．【答案】（1）证明：连接OD .∵DE 是⊙O 的切线 ∴OD ⊥DE ∵DE ⊥BC ∴OD ∥BC ∴∠ODA =∠C又∵OD=OA∴∠ODA=∠OAD ∴∠OAD=∠C∴AB=BC（2）解：连接BD ∵AB为直径∴∠BDA=90°∴∠BDC=90°∴△DEB∼△CED∴DEBE=CEDE∴3BE=63∴BE=3 2∴BC=15 2∴AB=15 220．【答案】（1）解：如图，连接OC∵DC切⊙O于C∴OC⊙CF∴⊙ADC＝⊙OCD＝90°∴AD //OC∴⊙DAC＝⊙OCA∵OA＝OC∴⊙OAC＝⊙OCA∴⊙DAC＝⊙OAC∵⊙BAD＝80°∴⊙DAC＝12⊙BAD＝12×80°＝40°（2）解：连接BC.∵AB是直径∴⊙ACB＝90°＝⊙ADC ∵⊙DAC＝⊙BAC∴⊙ADC⊙⊙ACB∴ACAB=ADAC∵AD＝6，AB＝8∴AC8=6AC∴AC＝4 √3.21．【答案】（1）∵AB为⊙O的直径∴∠ACB=90°∵AB=8cm，⊙BAC=30°∴BC=4∵OD⊙AC∴OD//BC∵OA=OB∴OD=12BC=2（2）△ADO是等腰三角形.理由如下：如图，过O作OQ⊥AC于Q,连接OC,∵AB=8,∠BAC=30°∴AC=AB·cos30°=8×√32=4√3∴CQ=AQ=2√3∴OQ=12OA=2设OD=x,则CD=2OD=2x∴DQ=2x−2√3由勾股定理可得：x2=(2x−2√3)2+22∴(√3x−4)2=0∴x1=x2=4√3 3∴AD=4√3−2×4√33=4√33=OD∴△ADO是等腰三角形.22．【答案】（1）证明：连接OD∵OD＝OB∴⊙ODB＝⊙OBD．∵AB是直径∴⊙ADB＝90°∴⊙CDB＝90°．∵E为BC的中点∴DE＝BE∴⊙EDB＝⊙EBD∴⊙ODB＋⊙EDB＝⊙OBD＋⊙EBD 即⊙EDO＝⊙EBO．∵BC是以AB为直径的⊙O的切线∴AB⊙BC∴⊙EBO ＝90°∴⊙ODE ＝90°∴DE 是⊙O 的切线（2）解：连接AE∵S 2＝5S 1，E 为BC 的中点∴S ⊙ACE ＝3S 1∴S ⊙ADE ＝2S 1∴AD =2DC∵⊙CBO ＝90°，⊙CDB ＝90° ∴⊙BDC⊙⊙ADB∴AD BD =DB DC∴DB 2＝AD •DC ，即 DB =√2DC∴DB AD =√2DC 2DC =√22∴tan⊙BAC ＝ DB AD =√2223．【答案】（1）解： ∵AB =AC AB ⏜=AC ⏜ ∵ 点 D 是 BC ⃗⃗⃗⃗⃗ 的中点∴BD ⏜=CD ⏜∴AB ⏜+BD ⏜=AC ⏜+CD ⏜∴ABD ⏜=ACD ⏜∴∠ACD =∠ABD =90°在 △ACF △ABE 中{∠A =∠A AB =AC ∠ABE =∠ACF∴△ACF ≌△ABE(ASA)∴CF =BE又 ∵BD ⏜=CD ⏜∴BD =CD∴CF −CD =BE −BD ，即 DF =DE （2）解：连接 AD由（1）知 ∠ACD =90°∴AD 是 ⊙O 的直径∴∠DCE =90°又 ∵CD =BD =6在 Rt △DCE 中令 AB =AC =x ，在 Rt △ABE 中由 AB 2+BE 2=AE 2 ，得 x 2+(6+10)2=(x +8)2 解得 x =12 ，即 AC =12在 Rt △ACD 中∴⊙O 的半径为 12AD =3√5 24．【答案】（1）证明：连接OD ．∵EF⊙AF∴⊙F ＝90°．∵D 是 BC⌢ 的中点，∴BD ⌢=CD ⌢ ． ∴⊙EOD ＝⊙DOC ＝ 12⊙BOC ∵⊙A ＝ 12⊙BOC ，∴⊙A ＝⊙EOD ∴OD⊙AF ．∴⊙EDO ＝⊙F ＝90°．∴OD⊙EF∴EF 是⊙O 的切线；（2）解：在Rt⊙AFE 中∵AF ＝6，EF ＝8 ∴AE =√AF 2+EF 2 ＝ √62+82 ＝10 设⊙O 半径为r ，∴EO ＝10﹣r ． ∵⊙A ＝⊙EOD ，⊙E ＝⊙E∴⊙EOD⊙⊙EAF ，∴OD AF ＝ OE EA ∴r 6=10−r 10 ．∴r ＝ 154 ，即⊙O 的半径为 154 ．。

初三数学圆专项练习题大全圆是数学中一个重要的几何概念，它在几何题中经常出现。

为了帮助初三学生更好地掌握圆的知识，以下是一份初三数学圆专项练习题的大全，包括了常见的圆的性质、弧与弦的关系、切线与割线等内容。

希望同学们通过这些练习题的训练，能够熟练掌握圆的相关知识，并能灵活运用于解题中。

1. 圆的面积计算题(1) 已知圆的半径为r，求圆的面积。

(2) 已知圆的直径为d，求圆的面积。

2. 圆的周长计算题(1) 已知圆的半径为r，求圆的周长。

(2) 已知圆的直径为d，求圆的周长。

3. 相关性质题(1) 在一个圆内，连接圆心和圆上一点A，再连接另一点B在圆上，证明线段AB是圆的半径。

(2) 若两圆相交于点A和点B，那么点A、点B与两圆心连线的关系是什么？(3) 圆的切线与半径的关系是什么？(4) 圆的割线与半径的关系是什么？4. 圆的切线与弦的关系题(1) 若AB是圆的切线，C是弦上一点，证明AB与直径AC的夹角等于角ACB。

(2) 若AD是圆的直径，B是圆上一点，证明ACB是直角。

5. 多边形与圆的关系题(1) 若一个正多边形的每个顶点均位于同一个圆上，那么这个正多边形的内角和是多少度？(2) 若一个正多边形的内角和等于360度，那么这个正多边形的每个顶点都位于同一个圆上吗？6. 圆的切线长度计算题(1) 已知切点A到圆心的距离为r，切线段AB的长度为x，求x的值。

7. 圆的弦长计算题(1) 已知弦CD的长度为x，求弦AB的长度。

8. 圆的切线长与切点到圆心距离关系题(1) 切线段AB长为12，切点到圆心的距离为5，求切点到圆的切线的长度。

以上是一部分初三数学圆专项练习题的大全，希望同学们能够认真训练，掌握圆的相关性质和计算方法。

通过不断的练习和巩固，相信你们一定能够在数学中取得更大的进步！。