【小初高学习】2017年中考数学第一部分考点研究复习第三章函数第15课时二次函数的实际应用真题精选含

2017年中考数学函数知识点一次函数与反比例函数考点一、平面直角坐标系 1、平面直角坐标系在平面内画两条互相垂直且有公共原点的数轴，就组成了平面直角坐标系。

其中，水平的数轴叫做x 轴或横轴，取向右为正方向；铅直的数轴叫做y 轴或纵轴，取向上为正方向；两轴的交点O （即公共的原点）叫做直角坐标系的原点；建立了直角坐标系的平面，叫做坐标平面。

为了便于描述坐标平面内点的位置，把坐标平面被x 轴和y 轴分割而成的四个部分，分别叫做第一象限、第二象限、第三象限、第四象限。

注意：x 轴和y 轴上的点，不属于任何象限。

2、点的坐标的概念点的坐标用（a ，b ）表示，其顺序是横坐标在前，纵坐标在后，中间有“，”分开，横、纵坐标的位置不能颠倒。

平面内点的坐标是有序实数对，当b a ≠时，（a ，b ）和（b ，a ）是两个不同点的坐标。

考点二、不同位置的点的坐标的特征 1、各象限内点的坐标的特征 点P(x,y)在第一象限0,0>>⇔y x点P(x,y)在第二象限0,0><⇔y x 点P(x,y)在第三象限0,0<<⇔y x 点P(x,y)在第四象限0,0<>⇔y x 2、坐标轴上的点的特征点P(x,y)在x 轴上0=⇔y ，x 为任意实数 点P(x,y)在y 轴上0=⇔x ，y 为任意实数点P(x,y)既在x 轴上，又在y 轴上⇔x ，y 同时为零，即点P 坐标为（0，0） 3、两条坐标轴夹角平分线上点的坐标的特征 点P(x,y)在第一、三象限夹角平分线上⇔x 与y 相等 点P(x,y)在第二、四象限夹角平分线上⇔x 与y 互为相反数 4、和坐标轴平行的直线上点的坐标的特征 位于平行于x 轴的直线上的各点的纵坐标相同。

位于平行于y 轴的直线上的各点的横坐标相同。

5、关于x 轴、y 轴或远点对称的点的坐标的特征点P 与点p ’关于x 轴对称⇔横坐标相等，纵坐标互为相反数点P 与点p ’关于y 轴对称⇔纵坐标相等，横坐标互为相反数 点P 与点p ’关于原点对称⇔横、纵坐标均互为相反数 6、点到坐标轴及原点的距离点P(x,y)到坐标轴及原点的距离： （1）点P(x,y)到x 轴的距离等于y （2）点P(x,y)到y 轴的距离等于x （3）点P(x,y)到原点的距离等于22y x + 考点三、函数及其相关概念 1、变量与常量在某一变化过程中，可以取不同数值的量叫做变量，数值保持不变的量叫做常量。

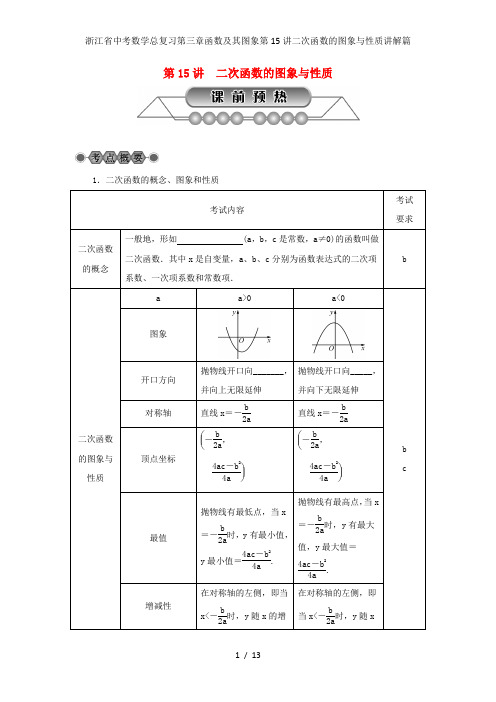
第15讲二次函数的图象与性质1．二次函数的概念、图象和性质考试内容考试要求二次函数的概念一般地，形如 (a，b，c是常数，a≠0)的函数叫做二次函数．其中x是自变量，a、b、c分别为函数表达式的二次项系数、一次项系数和常数项．b二次函数的图象与性质a a>0 a<0bc 图象开口方向抛物线开口向_______，并向上无限延伸抛物线开口向_____，并向下无限延伸对称轴直线x＝－b2a直线x＝－b2a顶点坐标⎝⎛－b2a，⎭⎪⎫4ac－b24a⎝⎛－b2a，⎭⎪⎫4ac－b24a最值抛物线有最低点，当x＝－b2a时，y有最小值，y最小值＝4ac－b24a.抛物线有最高点，当x＝－b2a时，y有最大值，y最大值＝4ac－b24a.增减性在对称轴的左侧，即当x<－b2a时，y随x的增在对称轴的左侧，即当x<－b2a时，y随x2.二次函数的图象与字母系数的关系3.确定二次函数的解析式考试内容考试要求方法 适用条件及求法c一般式若已知条件是图象上的三个点或三对自变量与函数的对应值，则可设所求二次函数解析式为____________________.顶点式若已知二次函数图象的顶点坐标或对称轴方程与最大值(最小值)，可设所求二次函数为____________________.交点式若已知二次函数图象与x 轴的两个交点的坐标为(x 1，0)，(x 2，0)，可设所求的二次函数为 ．4.二次函数与一元二次方程以及不等式之间的关系考试内容考试要求二次函数与一元二次方程二次函数y ＝ax 2＋bx ＋c 的图象与 轴的交点的 坐标是一元二次方程ax 2＋bx ＋c ＝0的根．b二次函数与不等式 抛物线y ＝ax 2＋bx ＋c 在x 轴上方的部分点的纵坐标都为正，所对应的x 的所有值就是不等式ax 2＋bx ＋c 0的解集；在x 轴下方的部分点的纵坐标均为负，所对应的x 的所有值就是不等式ax 2＋bx ＋c 0的解集．5.二次函数图象常见的变换考试内容考试要求平移顶点坐标的变化，按照“横坐标加减左右移”、“纵坐标加减上下移”的方法进行．c旋转 抛物线关于原点旋转180°，此时顶点关于原点对称，a 的符号相反． 轴对称抛物线关于x 轴对称，此时顶点关于x 轴对称，a 的符号相反；抛物b线关于y轴对称，此时顶点关于y轴对称，a的符号不变．考试内容考试要求基本思想数形结合，从二次函数的图象研究其开口方向、对称轴、顶点坐标、增减性、最值及其图象的平移变化，到利用二次函数图象求解方程与方程组，再到利用图象求解析式和解决实际问题，都体现了数形结合的思想．c1．(2015·台州)设二次函数y＝(x－3)2－4图象的对称轴为直线l，若点M在直线l 上，则点M的坐标可能是( )A．(1，0) B．(3，0) C．(－3，0) D．(0，－4)2．(2017·金华)对于二次函数y＝－(x－1)2＋2的图象与性质，下列说法正确的是( )A．对称轴是直线x＝1，最小值是2B．对称轴是直线x＝1，最大值是2C．对称轴是直线x＝－1，最小值是2D．对称轴是直线x＝－1，最大值是23．(2017·宁波)抛物线y＝x2－2x＋m2＋2(m是常数)的顶点在( )A．第一象限B．第二象限C．第三象限D．第四象限4．(2016·舟山)把抛物线y＝x2先向右平移2个单位，再向上平移3个单位，平移后抛物线的表达式是____________________．5．(2015·甘孜州)若二次函数y＝2x2的图象向左平移2个单位长度后，得到函数y＝2(x＋h)2的图象，则h＝____________________．【问题】如图是y＝ax2＋bx＋c(a≠0)的图象，且点A(－1，0)，B(3，0)．(1)你能从图象中想到哪些二次函数性质；(2)若点C为(0，－3)，你又能得到哪些结论．【归纳】通过开放式问题，归纳、疏理二次函数的图象与性质．类型一二次函数的解析式例1(1)已知抛物线的顶点坐标为(－1，－8)，且过点(0，－6)，则该抛物线的表达式为________；(2)已知二次函数y＝ax2＋bx＋c的图象经过A(－1，－1)、B(0，2)、C(1，3)；则二次函数的解析式为________；(3)已知抛物线过点A(2，0)，B(－1，0)，与y轴交于点C，且OC＝2.则这条抛物线的解析式为________．【解后感悟】解题关键是选择合适的解析式：当已知抛物线上三点求二次函数的关系式时，一般采用一般式y＝ax2＋bx＋c(a≠0)；当已知抛物线顶点坐标(或对称轴及最大或最小值)求关系式时，一般采用顶点式y＝a(x－h)2＋k；当已知抛物线与x轴的交点坐标求二次函数的关系式时，一般采用交点式y＝a(x－x1)(x－x2)．1．(1)(2017·杭州模拟)如图，已知抛物线y＝－x2＋bx＋c的对称轴为直线x＝1，且与x轴的一个交点为(3，0)，那么它对应的函数解析式是____________________．(2)(2017·长春模拟)已知二次函数的图象与x轴的两个交点A，B关于直线x＝－1对称，且AB＝6，顶点在函数y＝2x的图象上，则这个二次函数的表达式为____________________．类型二二次函数的图象、性质例2(1)对于抛物线y＝－(x＋1)2＋4，下列结论：①抛物线的开口向下；②对称轴为直线x＝1；③顶点坐标为(－1，4)；④x≥1时，y 随x的增大而减小；⑤当x＝－1时，y有最大值是4；⑥当y≥0时，－3≤x≤1；⑦点A(－2，y1)、B(1，y2)在抛物线上，则y1＞y2.其中正确结论是______________；(2)如图是二次函数y＝ax2＋bx＋c的图象，下列结论：①－2≤x≤1，二次函数y＝ax2＋bx＋c的最大值为4，最小值为0；②使y≤3成立的x 的取值范围是x≥0；③一元二次方程ax2＋bx＋c＝0的两根为x1＝－3，x2＝1；④一元二次方程ax2＋bx＋c－3＝0的两根为x1＝－2，x2＝0；⑤当二次函数的值大于一次函数y＝－x ＋3的值时，x取值范围是－1＜x＜0.其中正确结论是______________．【解后感悟】解题关键是正确把握解析式的特点、图象的特点、二次函数的性质，注意数形结合．2．(1)二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，下列说法：①2a＋b＝0；②当－1≤x≤3时，y<0；③若(x1，y1)、(x2，y2)在函数图象上，当x1<x2时，y1<y2；④9a＋3b＋c＝0；⑤4a－2b＋c＞0.其中正确的是____________________．(2)(2015·杭州)设函数y＝(x－1)[(k－1)x＋(k－3)](k是常数)．①当k取1和2时的函数y1和y2的图象如图所示，请你在同一直角坐标系中画出当k 取0时函数的图象；②根据图象，写出你发现的一条结论；③将函数y2的图象向左平移4个单位，再向下平移2个单位，得到函数y3的图象，求函数y3的最小值．类型三二次函数的图象变换例3已知抛物线y＝2(x－4)2－1.(1)将该抛物线先向左平移4个单位长度，再向上平移2个单位长度，平移后所得抛物线的解析式为________；(2)将该抛物线关于x轴作轴对称变换，再将所得的抛物线关于y轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为________．(3)将该抛物线绕它的顶点旋转180°，所得抛物线的解析式是________．【解后感悟】①平移的规律：左加右减，上加下减；②对称的规律：关于x轴对称的两点横坐标相同，纵坐标互为相反数；关于y轴对称的两点纵坐标相同，横坐标互为相反数；关于原点对称的两点横、纵坐标均互为相反数；③旋转的规律：旋转后的抛物线开口相反，顶点关于旋转点对称．3．(1)(2017·绍兴)矩形ABCD 的两条对称轴为坐标轴，点A 的坐标为(2，1)．一张透明纸上画有一个点和一条抛物线，平移透明纸，使这个点与点A 重合，此时抛物线的函数表达式为y ＝x 2，再次平移透明纸，使这个点与点C 重合，则该抛物线的函数表达式变为( )A ．y ＝x 2＋8x ＋14B ．y ＝x 2－8x ＋14C ．y ＝x 2＋4x ＋3D ．y ＝x 2－4x ＋3(2)(2017·盐城)如图，将函数y ＝12(x －2)2＋1的图象沿y 轴向上平移得到一条新函数的图象，其中点A(1，m)，B(4，n)平移后的对应点分别为点A′、B′.若曲线段AB 扫过的面积为9(图中的阴影部分)，则新图象的函数表达式是( )A ．y ＝12(x －2)2－2B ．y ＝12(x －2)2＋7 C ．y ＝12(x －2)2－5 D ．y ＝12(x －2)2＋4类型四 二次函数的综合问题例4 如图，抛物线y ＝－x 2＋2x ＋c 与x 轴交于A ，B 两点，它们的对称轴与x 轴交于点N ，过顶点M 作ME⊥y 轴于点E ，连结BE 交MN 于点F. 已知点A 的坐标为(－1，0)．(1)求该抛物线的解析式及顶点M 的坐标； (2)求△EMF 与△BNF 的面积之比．【解后感悟】抛物线与x 轴的交点问题；二次函数的性质；待定系数法的应用；曲线上点的坐标与方程的关系；相似三角形的判定和性质．4．(1)(2016·长春)如图，在平面直角坐标系中，菱形OABC的顶点A在x轴正半轴上，顶点C的坐标为(4，3)，D是抛物线y＝－x2＋6x上一点，且在x轴上方，则△BCD面积的最大值为____________________．(2)(2015·湖州)如图，已知抛物线C1∶y＝a1x2＋b1x＋c1和C2∶y＝a2x2＋b2x＋c2都经过原点，顶点分别为A，B，与x轴的另一个交点分别为M、N，如果点A与点B，点M与点N 都关于原点O成中心对称，则抛物线C1和C2为姐妹抛物线，请你写出一对姐妹抛物线C1和C2，使四边形ANBM恰好是矩形，你所写的一对抛物线解析式是和.类型五二次函数的应用例5(2017·杭州模拟)九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：售价(元/件) 100 110 120 130 …月销量(件) 200 180 160 140 …已知该运动服的进价为每件60元，设售价为x元．(1)请用含x的式子表示：①销售该运动服每件的利润是________元；②月销量是________件；(直接填写结果)(2)设销售该运动服的月利润为y元，那么售价为多少时，当月的利润最大，最大利润是多少？【解后感悟】此题是二次函数的应用，准确分析题意，列出y与x之间的二次函数关系式是解题关键．5．(2017·重庆模拟)我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两段抛物线组合而成的封闭图形，不妨简称为“锅线”，锅口直径为6dm，锅深3dm，锅盖高1dm(锅口直径与锅盖直径视为相同)，建立直角坐标系如图1所示(图2是备用图)，如果把锅纵断面的抛物线记为C1，把锅盖纵断面的抛物线记为C2.(1)求C1和C2的解析式；(2)如果炒菜锅里的水位高度是1dm，求此时水面的直径；(3)如果将一个底面直径为3dm，高度为3dm的圆柱形器皿放入炒菜锅内蒸食物，锅盖能否正常盖上？请说明理由．【探索研究题】如图，一段抛物线：y＝－x(x－3)(0≤x≤3)，记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…如此进行下去，直至得C13.若P(37，m)在第13段抛物线C13上，则m＝________．【方法与对策】本题是数形规律探究能力．图形类规律探索题，通常先把图形型问题转化为数字型问题，再从数字的特点来寻找规律，解题关键从操作中前面几个点的坐标位置变化，猜想、归纳出一般变化规律．该题型是图形变换和规律的探究题，是中考命题方向．【配方漏括号】用配方法求二次函数y＝512x2－53x＋54图象的顶点坐标及对称轴．参考答案第15讲二次函数的图象与性质【考点概要】1．y＝ax2＋bx＋c上下减小增大增大减小 2.上下小y左右原点 正 负 唯一 两个 没有 > < 3.y ＝ax 2＋bx ＋c y ＝a (x －m )2＋k y ＝a (x －x 1)(x －x 2) 4.x 横 > <【考题体验】1．B 2.B 3.A 4.y ＝(x －2)2＋3 5.2【知识引擎】【解析】(1)对称轴是直线x ＝1等；(2)当x ＝1时，y 的最小值为－4等．【例题精析】例1 (1)y ＝2(x ＋1)2－8；(2)y ＝－x 2＋2x ＋2；(3)y ＝x 2－x －2或y ＝－x 2＋x ＋2 例2 (1)①③④⑤⑥⑦；(2)①③④⑤ 例3 (1)y ＝2x 2＋1；(2)y ＝－2(x ＋4)2＋1；(3)y ＝－2(x －4)2－1 例4 (1)∵点A 在抛物线y ＝－x 2＋2x ＋c 上，∴－(－1)2＋2·(－1)＋c ＝0，解得：c ＝3，∴抛物线的解析式为y ＝－x 2＋2x ＋3.∵y＝－x 2＋2x ＋3＝－(x －1)2＋4，∴抛物线的顶点M(1，4)；(2)∵A(－1，0)，抛物线的对称轴为直线x ＝1，∴点B(3，0)．∴EM＝1，BN ＝2.∵EM∥BN，∴△EMF ∽△BNF.∴S △EMF S △BNF ＝⎝ ⎛⎭⎪⎫EM NB 2＝⎝ ⎛⎭⎪⎫122＝14. 例5 (1)①(x－60)；②(－2x ＋400) (2)依题意可得：y ＝(x －60)×(－2x ＋400)＝－2x 2＋520x －24000＝－2(x －130)2＋9800，当x ＝130时，y 有最大值9800.所以售价为每件130元时，当月的利润最大为9800元．【变式拓展】1．(1)y ＝－x 2＋2x ＋3 (2)y ＝29x 2＋49x －1692．(1)①④⑤ (2)①根据题意可得函数图象为：②图象都经过点(1，0)和点(－1，4)；图象总交x 轴于点(1，0)；k 取0和2时的函数图象关于点(0，2)成中心对称；③平移后的函数y 3的表达式为：y 3＝(x ＋3)2－2，∴当x ＝－3时，函数y 3的最小值为－2.3. (1)A (2)D4. (1)15 (2)y ＝－3x 2＋23x y ＝3x 2＋23x5.(1)由于抛物线C 1、C 2都过点A(－3，0)、B(3，0)，可设它们的解析式为：y ＝a(x －3)(x＋3)；抛物线C 1还经过D(0，－3)，则有：－3＝a(0－3)(0＋3)，解得：a ＝13，即：抛物线C 1：y ＝13x 2－3(－3≤x≤3)；抛物线C 2还经过C(0，1)，则有：1＝a(0－3)(0＋3)，解得：a ＝－19，即：抛物线C 2：y ＝－19x 2＋1(－3≤x≤3)．(2)当炒菜锅里的水位高度为1dm 时，y ＝－2，即13x 2－3＝－2，解得：x ＝±3，∴此时水面的直径为23dm . (3)锅盖能正常盖上，理由如下：当x ＝32时，抛物线C 1：y ＝13×⎝ ⎛⎭⎪⎫322－3＝－94，抛物线C 2：y ＝－19×⎝ ⎛⎭⎪⎫322＋1＝34，而34－⎝ ⎛⎭⎪⎫－94＝3，∴锅盖能正常盖上． 【热点题型】【分析与解】C 1：y ＝－x(x －3)(0≤x≤3)C 2：y ＝(x －3)(x －6)(3≤x≤6)C 3：y ＝－(x －6)(x －9)(6≤x≤9)C 4：y ＝(x －9)(x －12)(9≤x≤12)…C 13：y ＝－(x －36)(x －39)(36≤x≤39)，当x ＝37时，y ＝2，所以，m ＝2.【错误警示】y ＝512x 2－53x ＋54＝512(x 2－4x ＋3)＝512[(x －2)2－1]＝512(x －2)2－512，∴该函数图象的顶点坐标是(2，－512)，对称轴是直线x ＝2.。

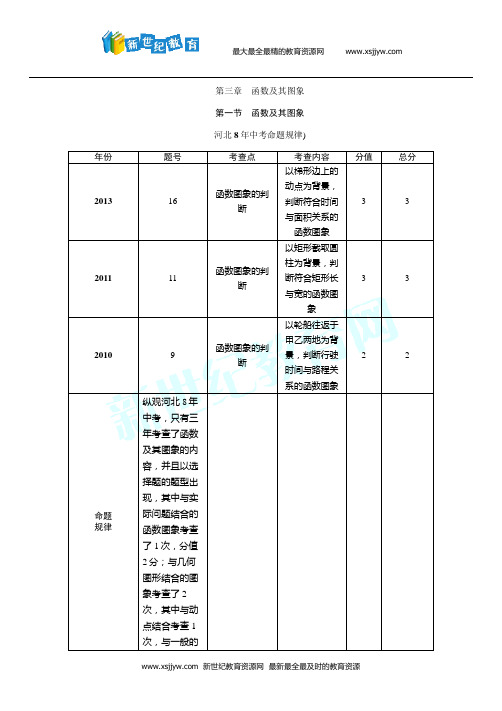
第三章函数及其图象第一节函数及其图象河北8年中考命题规律)年份题号考查点考查内容分值总分201316 函数图象的判断以梯形边上的动点为背景，判断符合时间与面积关系的函数图象3 3201111 函数图象的判断以矩形截取圆柱为背景，判断符合矩形长与宽的函数图象3 320109 函数图象的判断以轮船往返于甲乙两地为背景，判断行驶时间与路程关系的函数图象2 2命题规律纵观河北8年中考，只有三年考查了函数及其图象的内容，并且以选择题的题型出现，其中与实际问题结合的函数图象考查了1次，分值2分；与几何图形结合的图象考查了2次，其中与动点结合考查1次，与一般的几何图形结合考查了1次，分值3分．命题预测预计2017年河北中考，本课时的重点考查对象为函数图象的判断，可能会与其他知识结合，特别是与几何图形相结合的图象，题型以选择题为主.河北8年中考真题及模拟)与实际问题结合的函数图象(1次)1．(2010河北9题2分)一艘轮船在同一航线上往返于甲、乙两地．已知轮船在静水中的速度为15 km/h，水流速度为5 km/h.轮船先从甲地顺水航行到乙地，在乙地停留一段时间后，又从乙地逆水航行返回到甲地．设轮船从甲地出发后所用时间为t(h)，航行的路程为s(m)，则s与t的函数图象大致是(C),A),B),C),D)与几何图形结合的函数图象(2次)2．(2011河北11题3分)如图，在矩形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长和宽分别为y和x，则y与x的函数图象大致是(A),A) ,B),C ) ,D )3．(2013河北16题3分)如图，在梯形ABCD 中，AB ∥DC ，DE ⊥AB ，CF ⊥AB ，且AE ＝EF ＝FB ＝5，DE ＝12，动点P 从点A 出发，沿折线AD —DC —CB 以每秒1个单位长的速度运动到点B 停止．设运动时间为t s ，y ＝S △EPF ，则y 与t 的函数图象大致是( A ),A ) ,B ) ,C ) ,D )4．(2016河北石家庄四十三中二模)小丽从家开车出发前去观看某比赛活动，途中发现忘了带门票，于是打电话让妈妈马上从家里送来，同时小丽也往回开，遇到妈妈后聊了一会儿，接着继续开车往比赛现场．设小丽从家出发后所用时间为t ，小丽与比赛现场的距离为s.下面能反映s 与t 的函数关系的大致图象是( B ),A ) ,B ) ,C ) ,D )5．(2016沧州八中一模)某栏目的一名记者乘汽车赴360 km 外的农村采访，全程的前一部分为高速公路，后一部分为乡村公路．若汽车在高速公路和乡村公路上分别以某一速度匀速行驶，汽车行驶的路程y(km )与时间x(h )之间的关系如图所示，则下列结论正确的是( C )A ．汽车在高速公路上的行驶速度为100 km /hB ．乡村公路总长为90 kmC ．汽车在乡村公路上的行驶速度为60 km /hD ．该记者在出发后4.5 h 到达采访地6．(2016石家庄二十八中一模)在平面直角坐标系中点P(－a 2－1，2)，在( B ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限7．(2015石家庄二模)如图，在Rt △ABC 中，∠C ＝90°，AB ＝5 cm ，BC ＝3 cm ，动点P 从点A 出发，以每秒1 cm 的速度，沿A →B →C 的方向运动，到达点C 时停止．若设y ＝PC 2，运动时间为t s ，则能反映y 与t 之间函数关系的图象大致是( A ),A ) ,B ),C ) ,D )8．(2016河北石家庄二十八中一模)点P(2，3)关于x 轴的对称点的坐标为__(2，－3)__．9．(2016承德一模)函数y ＝21－x ＋1x中，自变量x 的取值范围是__x<1且x ≠0__．10．(2016保定十七中二模)小明从家跑步到学校，接着马上原路步行回家．如图是小明离家的路程y(m )与时间t(min )的函数图象，则小明回家的速度是__80__m /min .11．(2016保定十七中二模)在△ABC 中，点P 从B 点开始出发向C 点运动，在运动过程中，设线段AP 的长为y ，线段BP 的长为x[如图(1)]，y 关于x 的函数图象如图(2)所示．Q(1，3)是函数图象上的最低点．请仔细观察图(1)，图(2)，解答下列问题：(1)请直接写出AB 边的长和BC 边上的高AH 的长； (2)求∠B 的度数；(3)若△ABP 为钝角三角形，求x 的取值范围．解：(1)由图(1)及Q(1，3)是函数图象的最低点，知AH ＝3，BH ＝1，∴AB ＝AH 2＋BH 2＝2；(2)当点P 运动到点H 时，此时BH ＝1，AH ＝3，在Rt △ABH 中，AH ＝3，BH ＝1，tan B ＝3，故∠B ＝60°；(3)①当∠APB 为钝角时，此时可得0<x<1；②如图：过点A 作AP ⊥AB ，则BP ＝ABcos B＝4， 由题意，知BC ＝6.即当4<x ≤6时，∠BAP 为钝角．综上，可得0<x<1或4<x ≤6时，△ABP 为钝角三角形．,中考考点清单)平面直角坐标系及点的坐标1．有序实数对：坐标平面上任意一点都可以用唯一一对有序实数来表示；反过来，任意一对有序实数都可以表示坐标平面上唯一一个点．【方法技巧】一般地，点P(a ，b)到x 轴的距离为|b|；到y 轴的距离为|a|；到原点的距离为a 2＋b 2.2．平面直角坐标系中点的坐标特征各象限点的坐标的符号特征第一象限(＋，＋)；第二象限①__(－，＋)__；第三象限(－，－)；第四象限②__(＋，－)__坐标轴上点的坐标特征 x 轴上的点的纵坐标为③__0__，y 轴上的点的横坐标为0，原点的坐标为(0，0)各象限角平分线上点的坐标特征第一、三象限角平分线上的横、纵坐标相等；第二、四象限角平分线上的横、纵坐标④__互为相反数__ 对称点的坐标特征点P(a ，b)关于x 轴对称的点的坐标为(a ，－b)；点P(a ，b)关于y 轴对称的点的坐标为⑤__(－a ，b)__；点P(a ，b)关于原点对称的点的坐标为P′(－a ，－b) 平移点的坐标特征将点P(x ，y)向右或向左平移a 个单位，得到对应点的坐标P′是(x ＋a ，y)或(x －a ，y)；将点P(x ，y)向上或向下平移b 个单位，得到对应点的坐标P′是(x ，y ＋b)或(x ，y －b)；将点P(x ，y)向右或向左平移a 个单位，再向上或向下平移b 个单位，得到对应点P′是⑥__(x ＋a ，y ＋b)或(x －a ，y －b)__，简记为：左减右加，上加下减函数的相关概念3．变量：在一个变化过程中，可以取不同数值的量叫做变量． 4．常量：在一个变化过程中，数值保持不变的量叫做常量．5．函数：一般地，在某个变化过程中，有两个变量x 和y.如果给定x 的一个值，就能相应地确定y 的一个值，那么，我们就说y 是x 的函数．其中，x 叫做自变量．函数自变量的取值范围6.解析式 取值范围 整式型 取全体实数 分式型，如y ＝ax分母不为0，即x ≠0 根式型，如y ＝x 被开方数大于等于0，即x ≥0分式＋根式型，如y ＝ax同时满足两个条件：①被开方数大于等于0即x ≥0；②分母不为0，即x ≠0函数的表示方法及其图象(河北中考10，11，13年考查了本考点)函数图象的判断近8年共考查3次，题型都为选择题，出题背景有：(1)与实际问题结合；(2)与几何图形结合；(3)与几何图形中的动点问题结合，设问方式均为“判断函数图象大致是”．7．表示方法：数值表、图象、解析式是函数关系的三种不同表达形式，它们分别表现出具体、形象直观和便于抽象应用的特点．8．图象的画法：知道函数的解析式，一般用描点法按下列步骤画出函数的图象．(1)取值．根据函数的解析式，取自变量的一些值，得出函数的对应值，按这些对应值列表；(2)画点．根据自变量和函数的数值表，在直角坐标系中描点；(3)连线．用平滑的曲线将这些点连接起来，即得函数的图象．9．已知函数解析式，判断点P(x，y)是否在函数图象上的方法：若点P(x，y)的坐标适合函数解析式，则点P(x，y)在其图象上；若点P(x，y)的坐标不适合函数解析式，则点P(x，y)不在其图象上．【方法技巧】判断符合题意的函数图象的方法(1)与实际问题结合：判断符合实际问题的函数图象时，需遵循以下几点：①找起点：结合题干中所给自变量及因变量的取值范围，对应到图象中找相对应点；②找特殊点：即指交点或转折点，说明图象在此点处将发生变化；③判断图象趋势：判断出函数的增减性；④看是否与坐标轴相交：即此时另外一个量为0.(2)与几何图形(含动点)结合：以几何图形为背景判断函数图象的题目，一般的解题思路为设时间为t，找因变量与t之间存在的函数关系，用含t的式子表示，再找相对应的函数图象，要注意的是是否需要分类讨论自变量的取值范围．(3)分析函数图象判断结论正误分清图象的横纵坐标代表的量及函数中自变量的取值范围，同时也要注意：①分段函数要分段讨论；②转折点：判断函数图象的倾斜方向或增减性发生变化的关键点；③平行线：函数值随自变量的增大而保持不变．再结合题干推导出实际问题的运动过程，从而判断结论的正误．中考重难点突破)平面直角坐标系中点的坐标特征【例1】(2016白银中考)已知点P(0，m)在y轴的负半轴上，则点M(－m，－m＋1)在()A．第一象限B．第二象限C．第三象限D．第四象限【解析】由坐标轴上点的坐标特征确定m的取值范围，再判断点M的坐标符号，从而判断点M在第几象限．【学生解答】A1．(2016重庆中考)在平面直角坐标系中，若点P的坐标为(－3，2)，则点P所在的象限是(B)A．第一象限B．第二象限C．第三象限D．第四象限函数自变量的取值范围【例2】(2016内江中考)在函数y＝x－3x－4中，自变量x的取值范围是()A．x>3 B．x≥3C ．x>4D ．x ≥3且x ≠4 【学生解答】D2．(2016保定二模)函数y ＝x ＋1＋2x中，自变量x 的取值范围是__x ≥－1且x ≠0__．函数图象的判断【例3】(2016营口中考)如图，在矩形ABCD 中，AB ＝2，AD ＝3，点E 是BC 边上靠近点B 的三等分点，动点P 从点A 出发，沿路径A →D →C →E 运动，则△APE 的面积y 与点P 经过的路径长x 之间的函数关系用图象表示大致是( ),A ) ,B ) ,C ) ,D )【解析】∵在矩形ABCD 中，AB ＝2，AD ＝3，∴CD ＝AB ＝2，BC ＝AD ＝3，∵点E 是BC 边上靠近点B 的三等分点，∴CE ＝23×3＝2.①点P 在AD 上时，△APE 的面积y ＝12x ·2＝x(0≤x ≤3)；②点P 在CD 上时，S △APE ＝S四边形AECD －S △ADP －S △CEP ＝12×(2＋3)×2－12×3×(x －3)－12×2×(3＋2－x)＝5－32x ＋92－5＋x ＝－12x ＋92，所以y ＝－12x ＋92(3＜x ≤5)；③点P 在CE 上时，S △APE ＝12×(3＋2＋2－x)×2＝－x ＋7，所以y ＝－x ＋7(5＜x ≤7)，纵观各选项，只有A 选项图形符合． 【学生解答】A【方法指导】根据动点P 的运动路径A →D →C →E 可得，在计算△APE 的面积时应该分为3种情况，①当P 在AD 上时；②当P 在DC 上时；③当P 在CE 上时，分别计算出即可．要注意转折点有x ＝3时和x ＝5时．3．(2016白银中考)如图，△ABC 是等腰直角三角形，∠A ＝90°，BC ＝4，点P 是△ABC 边上一动点，沿B →A →C 的路径移动，过点P 作PD ⊥BC 于点D ，设BD ＝x ，△BDP 的面积为y ，则下列能大致反映y 与x 函数关系的图象是( B ),A ) ,B ),C ),D ),中考备考方略)1．(2016襄阳中考)如图，是一台自动测温仪记录的图象，它反映了我市冬季某天气温T 随时间t 变化而变化的关系，观察图象得到下列信息，其中错误的是( C )A ．凌晨4 h 气温最低为－3℃B ．14 h 气温最高为8℃C ．从0 h 至14 h ，气温随时间增长而上升D ．从14 h 至24 h ，气温随时间增长而下降2．(2016石家庄四十二中模拟)在平面直角坐标系中，点P(－3，2)关于直线y ＝x 对称点的坐标是( C ) A ．(－3，－2) B ．(3，2) C ．(2，－3) D ．(3，－2)3．(2016福州中考)平面直角坐标系中，已知▱ABCD 的三个顶点坐标分别是A(m ，n)，B(2，－1)，C(－m ，－n)，则点D 的坐标是( A )A ．(－2，1)B ．(－2，－1)C ．(－1，－2)D ．(－1，2)4．(2016烟台中考)如图，在平面直角坐标系中，正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形，且相似比为13，点A ，B ，E 在x 轴上，若正方形BEFG 的边长为6，则C 点坐标为( A )A ．(3，2)B ．(3，1)C ．(2，2)D ．(4，2)5．(2016济宁中考)匀速地向一个容器内注水，最后把容器注满．在注水过程中，水面高度h 随时间t 的变化规律如图所示(图中OABC 为一折线)．这个容器的形状是下图中哪一个( C ),A ) ,B ),C ) ,D ) 6．(2016齐齐哈尔中考)在函数y ＝3x ＋1x －2中，自变量x 的取值范围是__x ≥－13且x ≠2__．7．(2016莆田中考)甲车从A 地驶往B 地，同时乙车从B 地驶往A 地，两车相向而行，匀速行驶．甲车距B 地的距离y(km )与行驶时间x(h )的函数关系如图所示，乙车的速度是60 km /h .(1)求甲车的速度；(2)当甲乙两车相遇后，乙车速度变为a(km /h )，并保持匀速行驶，甲车速度保持不变，结果乙车比甲车晚38 min 到达终点，求a 的值．解：(1)V 甲＝280－1202＝80(km /h )．(2)相遇时间为28080＋60＝2(h )．依题意得60×280＋3860＝80×2a，解得a ＝75.经检验：a ＝75是原分式方程的解．8．(2016自贡中考)小刚以400 m /min 的速度匀速骑车5 min ，在原地休息了6 min ，然后以500 m /min 的速度骑回出发地．下列函数图象能表达这一过程的是( C ),A ) ,B ),C ) ,D )9．(2016龙东中考)如图，直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上，三角形沿水平方向从左向右匀速穿过正方形．设穿过时间为t ，正方形与三角形不重合部分的面积为S(阴影部分)，则S 与t 的大致图象为( A ),A ) ,B ),C ) ,D )10．(2016重庆中考)为了增强学生体质，某中学在体育课中加强了学生的长跑训练．在一次女子800 m 耐力测试中，小静和小茜在校园内200 m 的环形跑道上同时起跑，同时到达终点，所跑的路程s(m )与所用的时间t(s )之间的函数图象如图所示，则她们第一次相遇的时间是起跑后的第__120__s .11．(2016绍兴中考)小敏上午8：00从家里出发，骑车去一家超市购物，然后从这家超市返回家中．小敏离家的路程y(m )和所经过的时间x(min )之间的函数图象如图所示．请根据图象回答下列问题．(1)小敏去超市途中的速度是多少？在超市逗留了多长时间？ (2)小敏几点几分返回到家？解：(1)小敏去超市途中的速度是3 000÷10＝300(m /min )；在超市逗留的时间为40－10＝30(min )； (2)返回家途中的速度为(3 000－2 000)÷(45－40)＝200(m /min )， ∴回家所用时间为3 000÷200＝15(min )． ∴小敏从出发到回家共用40＋15＝55(min )． ∴小敏8点55分返回到家．12．(2016南宁中考)在一条笔直的公路上有A ，B 两地，甲骑自行车从A 地到B 地，乙骑自行车从B 地到A 地，到达A 地后立即按原路返回，下图是甲、乙两人离B 地的距离y(km )与行驶时间x(h )之间的函数图象，根据图象解答以下问题：(1)写出A ，B 两地之间的距离．(2)求出点M 的坐标，并解释该点坐标所表示的实际意义．(3)若两人之间保持的距离不超过3 km 时，能够用无线对讲机保持联系，请直接写出甲、乙两人能够用无线对讲机保持联系时x 的取值范围．解：(1)x ＝0时，甲距离B 地30 km ，∴A ，B 两地的距离为30 km . (2)由图，可知甲的速度为30÷2＝15(km /h )，乙的速度为30÷1＝30(km /h )，30÷(15＋30)＝23(h )，23×30＝20(km )，∴点M 的坐标为⎝⎛⎭⎫23，20，表示23h 后两人相遇，此时两人距离B 地20 km . (3)设x h 时，甲、乙两人相距3 km ，①若是相遇前，则15x ＋30x ＝30－3，解得x ＝35；②若是相遇后，则15x ＋30x ＝30＋3，解得x ＝1115；③若是到达B 地前，则15x －30(x －1)＝3，解得x ＝95，所以当35≤x ≤115或95≤x ≤2时，甲、乙两人能够用无线对讲机保持联系．。

2017年中考数学一次函数知识点总结和2017年中考数学三轮复习计划汇编2017年中考数学一次函数知识点总结一、定义与定义式：自变量x和因变量y有如下关系：y=kx+b则此时称y是x的一次函数。

特别地，当b=0时，y是x的正比例函数。

即：y=kx（k为常数，k≠0）二、一次函数的性质：1.y的变化值与对应的x的变化值成正比例，比值为k即：y=kx+b（k为任意不为零的实数b取任何实数）2.当x=0时，b为函数在y轴上的截距。

三、一次函数的图像及性质：1.作法与图形：通过如下3个步骤（1）列表；（2）描点；（3）连线，可以作出一次函数的图像——一条直线。

因此，作一次函数的图像只需知道2点，并连成直线即可。

（通常找函数图像与x轴和y轴的交点）2.性质：（1）在一次函数上的任意一点P（x，y），都满足等式：y=kx+b。

（2）一次函数与y轴交点的坐标总是（0，b），与x轴总是交于（-b/k，0）正比例函数的图像总是过原点。

3.k，b与函数图像所在象限：当k0时，直线必通过一、三象限，y随x的增大而增大；当k0时，直线必通过二、四象限，y随x的增大而减小。

当b0时，直线必通过一、二象限；当b=0时，直线通过原点当b0时，直线必通过三、四象限。

特别地，当b=O时，直线通过原点O（0，0）表示的是正比例函数的图像。

这时，当k0时，直线只通过一、三象限；当k0时，直线只通过二、四象限。

四、确定一次函数的表达式：已知点A（x1，y1）；B（x2，y2），请确定过点A、B的一次函数的表达式。

（1）设一次函数的表达式（也叫解析式）为y=kx+b。

（2）因为在一次函数上的任意一点P（x，y），都满足等式y=kx+b。

所以可以列出2个方程：y1=kx1+b……①和y2=kx2+b……②（3）解这个二元一次方程，得到k，b的值。

（4）最后得到一次函数的表达式。

五、一次函数在生活中的应用：1.当时间t一定，距离s是速度v的一次函数。

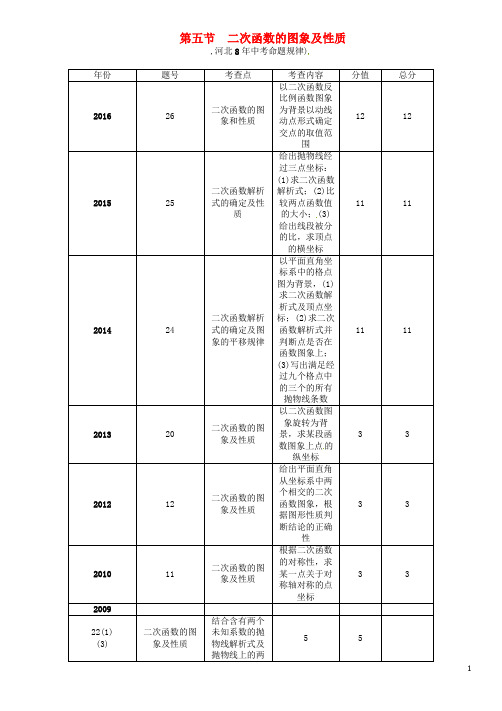
第五节二次函数的图象及性质,河北8年中考命题规律)年份题号考查点考查内容分值总分201626 二次函数的图象和性质以二次函数反比例函数图象为背景以动线动点形式确定交点的取值范围12 12201525 二次函数解析式的确定及性质给出抛物线经过三点坐标：(1)求二次函数解析式；(2)比较两点函数值的大小；(3)给出线段被分的比，求顶点的横坐标11 11201424 二次函数解析式的确定及图象的平移规律以平面直角坐标系中的格点图为背景，(1)求二次函数解析式及顶点坐标；(2)求二次函数解析式并判断点是否在函数图象上；(3)写出满足经过九个格点中的三个的所有抛物线条数11 11201320 二次函数的图象及性质以二次函数图象旋转为背景，求某段函数图象上点的纵坐标3 3201212 二次函数的图象及性质给出平面直角从坐标系中两个相交的二次函数图象，根据图形性质判断结论的正确性3 3201011 二次函数的图象及性质根据二次函数的对称性，求某一点关于对称轴对称的点坐标3 3200922(1) (3) 二次函数的图象及性质结合含有两个未知系数的抛物线解析式及5 5点，(1)求二次函数最小值及t的值；(3)直接写出满足条件的t的值22(2) 二次函数的图象及性质结合含有两个未知系数的抛物线解析式及抛物线上的两点，(2)求二次函数系数的值及开口方向4 4命题规律二次函数的图象及性质在中考中一般设置1道题，分值为2～11分，在选择、填空和解答题中均有涉及．分析近8年河北中考试题可以看出，本课时常考类型有：(1)二次函数解析式的确定(在解答题中考查了3次)；(2)二次函数图象的分析与判断(在选择题中考查了2次)；(3)以二次函数图象及性质的相关计算(在选择题中考查了2次，在填空题中考查了1次，在解答题中考查了1次)；(4)以二次函数、反比例函数为背景，涉及动线动点问题．(2016年)命题预测预计2017年中考，对于二次函数的考查以增减性、最值、函数图象判断以动点的坐标变化.,河北8年中考真题及模拟)二次函数的图象及性质(6次)1．(2010河北11题3分)如图，已知抛物线y＝x2＋bx＋c的对称轴为直线x＝2，点A，B均在抛物线上，且AB与x轴平行，其中点A的坐标为(0，3)，则点B的坐标为( D)A．(2，3) B．(3，2) C．(3，3) D．(4，3)(第1题图)(第2题图)2．(2012河北12题3分)如图，抛物线y 1＝a(x ＋2)2－3与y 2＝12(x －3)2＋1交于点A(1，3)，过点A 作x 轴的平行线，分别交两条抛物线于点B ，C.则以下结论：①无论x 取何值，y 2的值总是正数；②a＝1；③当x ＝0时，y 2－y 1＝4；④2AB＝3AC.其中正确结论是( D )A ．①②B ．②③C ．③④D ．①④3．(2014河北24题11分)如图，2×2网格(每个小正方形的边长为1)中有A ，B ，C ，D ，E ，F ，G ，H ，O 九个格点．抛物线l 的解析式为y ＝(－1)n x 2＋bx ＋c(n 为整数)．(1)n 为奇数，且l 经过点H(0，1)和C(2，1)，求b ，c 的值，并直接写出哪个格点是该抛物线的顶点； (2)n 为偶数，且l 经过点A(1，0)和B(2，0)，通过计算说明点F(0，2)和H(0，1)是否在该抛物线上； (3)若l 经过这九个格点中的三个，直接写出所有满足这样条件的抛物线条数．解：(1)b ＝2，c ＝1，E(1，2)是抛物线l 的顶点；(2)点F(0，2)在抛物线y ＝x 2－3x ＋2的图象上，点H(0，1)不在抛物线y ＝x 2－3x ＋2的图象上；(3)所有满足条件的抛物线共有8条．二次函数解析式的确定(2次)4．(2016保定十七中模拟)如图，正方形ABCD的边长为10，四个全等的小正方形的对称中心分别在正方形ABCD的顶点上，且它们的各边与正方形ABCD各边平行或垂直．若小正方形的边长为x，且0＜x≤10，阴影部分的面积为y，则能反映y与x之间函数关系的大致图象是( D),A) ,B),C) ,D) 5．(2016河北沧州十四中一模)已知二次函数y＝x2－4x＋5，函数的顶点坐标为( B)A．(－2，－1) B．(2，1)6．(2016河北石家庄二十八中一模)如果将抛物线y ＝x 2＋2向下平移1个单位，那么所得新抛物线的解析式是( C )A ．y ＝(x －1)2＋2B ．y ＝(x ＋1)2＋2C ．y ＝x 2＋1D ．y ＝x 2＋37．(2016河北石家庄四十一中一模)将二次函数y ＝x 2－2x ＋3化为y ＝(x －h)2＋k 的形式，结果为( D ) A ．y ＝(x ＋1)2＋4 B ．y ＝(x ＋1)2＋2 C ．y ＝(x －1)2＋4 D ．y ＝(x －1)2＋28．(2016河北保定十三中一模)已知二次函数y ＝ax 2＋bx ＋c 的图象如图所示，则在同一坐标系中，一次函数y ＝ax ＋c 和反比例函数y ＝ax的图象大致是( D ),A ) ,B ),C ) ,D )9．(2016河北石家庄四十三中一模)已知二次函数y ＝2(x －3)2＋1.下列说法：①其图象的开口向下；②其图象的对称轴为直线x ＝－3；③其图象顶点坐标为(3，－1)；④当x<3时，y 随x 的增大而减小．其中说法正确的有( A )A ．1个B ．2个C ．3个D ．4个10．(2016河北邯郸二十三中二模)二次函数y ＝ax 2＋bx ＋1(a≠0)的图象的顶点在第一象限，且过点(－1，0)．设t ＝a ＋b ＋1，则t 值的变化范围是( B )A ．0<t<1B ．0<t<2C ．1<t<2D ．－1<t<111．(2016河北保定十七中一模)已知抛物线y ＝x 2－x －1与x 轴的一个交点为(m ，0)，则代数式m 2－m ＋2 015的值为__2__016__．12．(20162y 的对应值如下表：__①③④__①抛物线与x 轴的一个交点为(3，0)；②函数y ＝ax 2＋bx ＋c 的最大值为6；③抛物线的对称轴是直线x ＝12；④在对称轴左侧，y 随x 增大而增大．13．(2016石家庄二十八中一模)已知抛物线y ＝ax 2＋bx 经过点A(－3，－3)和点P(t ，0)，且t≠0. (1)若该抛物线的对称轴经过点A ，如图，请通过观察图象，指出此时y 的最小值，并写出t 的值； (2)若t ＝－4，求a ，b 的值，并指出此时抛物线的开口方向； (3)直接写出使该抛物线开口向下的t 的一个值．解：(1)－3；－6；(2)a＝1，b＝4，开口向上；(3)－1.(答案不唯一，写出t＞－3且t≠0或其中任意一个数均可)14．(2015河北25题11分)如图，已知点O(0，0)，A(－5，0)，B(2，1)，抛物线l：y＝－(x－h)2＋1(h为常数)与y轴的交点为C.(1)l经过点B，求它的解析式，并写出此时l的对称轴及顶点坐标；(2)设点C的纵坐标为y C，求y C的最大值，此时l上有两点(x1，y1)，(x2，y2)，其中x1＞x2≥0，比较y1与y2的大小；(3)当线段OA被l只分为两部分，且这两部分的比是1∶4时，求h的值．解：(1)把x＝2，y＝1代入y＝－(x－h)2＋1，得h＝2.∴解析式为y＝－(x－2)2＋1(或y＝－x2＋4x－3)．对称轴为直线x＝2，顶点B(2，1)；(2)点C的横坐标为0，则y C＝－h2＋1，∴当h＝0时，y C有最大值为1.此时，l为y＝－x2＋1，对称轴为y轴，当x≥0时，y随着x的增大而减小，∴x1＞x2≥0时，y1＜y2；(3)把OA 分1∶4两部分的点为(－1，0)或(－4，0)．把x＝－1，y＝0代入y＝－(x－h)2＋1，得h＝0或h＝－2.但h＝－2时，OA被分为三部分，不合题意，舍去．同样，把x＝－4，y＝0代入y＝－(x－h)2＋1，得h＝－5或h＝－3(舍去)．∴h的值为0或－5.,中考考点清单)二次函数的概念及解析式1．定义：一般地，如果两个变量x 和y 之间的函数关系，可以表示成y ＝ax 2＋bx ＋c(a ，b ，c 是常数，且a≠0)，那么称y 是x 的二次函数，其中，a 叫做二次项系数，b 叫作一次项系数，c 叫做常数项．2．三种表示方法：(1)一般式：y ＝ax 2＋bx ＋c(a≠0)；(2)顶点式：y ＝a(x －h)2＋k(a≠0)，其中二次函数的顶点坐标是(h ，k)；(3)交点式：y ＝a(x －x 1)(x －x 2)(a≠0)，其中x 1，x 2为抛物线与x 轴交点的横坐标． 3．三种解析式之间的关系顶点式――→确定一般式――→因式分解两点式 4．二次函数解析式的确定(1)求解二次函数解析式的方法一般用待定系数法，根据所给条件的不同，要灵活选用函数解析式； A ．当已知抛物线上任意三点时，通常设为一般式y ＝ax 2＋bx ＋c 形式；B ．当已知抛物线的顶点或对称轴时，通常设为顶点式y ＝a(x －h)2＋k 形式；C ．当已知抛物线与x 轴的交点或交点横坐标时，通常设为两点式y ＝a(x －x 1)(x －x 2)． (2)步骤：①设二次函数的解析式；②根据已知条件，得到关于待定系数的方程组；③解方程组，求出待定系数的值，从而写出函数的解析式．二次函数的图象及其性质(高频考点)索结合的旋转抛物线；(2)以两个抛物线结合为背景；(3)与正方形结合．设问方式有：(1)求点坐标；(2)判断结论的正误；(3)判断不符合条件的函数图象；(4)求解析式；(5)求最值．5．图象性质函数二次函数y＝ax2＋bx＋c(a，b，c为常数，a≠0)图象对称轴直线x＝①__－b2a__ 直线x＝－b2a顶点坐标(－b2a，4ac－b24a) (－b2a，4ac－b24a)增减性在对称轴的左侧，即x＜－b2a时，y随x的增大而减小；在对称轴的右侧，即当x＞－b2a时，y随x的增大而增大，简记为左减右增在对称轴的左侧，即当x＜－b2a时，y随x的增大而增大；在对称轴的右侧，即当x＞－b2a时，y随x的增大而减小，简记为左增右减最值抛物线有最低点，当②__x＝－b2a__时，y有最小值，y最小值＝4ac－b24a抛物线有最高点，当x＝－b2a时，y有最大值，y最大值＝③__4ac－b24a__6.系数a，b，c与二次函数的图象关系项目字母字母的符号图象的特征aa＞0 开口向上a＜0 ④__开口向下__bb＝0 对称轴为y轴ab＞0(b与a同号) 对称轴在y轴左侧ab＜0(b与a异号) 对称轴在y轴右侧cc＝0 ⑤__经过原点__c＞0 与y轴正半轴相交c＜0 与y轴负半轴相交b2－4acb2－4ac＝0 与x轴有唯一交点(顶点)b2－4ac＞0 与x轴有两个不同交点b2－4ac＜0 与x轴没有交点特殊关系当x＝1时，y＝a＋b＋c若a －b ＋c ＞0，即x ＝－1时，y ＞0二次函数图象的平移7．平移步骤：(1)将抛物线解析式转化为顶点式y ＝a(x －h)2＋k ，确定其顶点坐标； (2)保持抛物线的形状不变，平移顶点坐标(h ，k)即可． 8．平移规律：二次函数与一元二次方程的关系9．当抛物线与x 轴有两个交点时，两交点的横坐标就是对应的一元二次方程的两个不相等的实数根． 10．当抛物线与x 轴只有一个交点时，该交点的横坐标就是对应的一元二次方程的两个相等的实数根． 11．当抛物线与x 轴没有交点时，对应的一元二次方程无实数根．移动方向 平移前的解析式 平移后的解析式 规律 向左平移 m 个单位 y ＝a(x －h)2＋k y ＝a(x －h ＋m)2＋k 左加 向右平移 m 个单位 y ＝a(x －h)2＋k y ＝a(x －h －m)2＋k 右减 向上平移 m 个单位 y ＝a(x －h)2＋k y ＝a(x －h)2＋k ＋m 上加 向下平移 m 个单位y ＝a(x －h)2＋ky ＝a(x －h)2＋k －m下减 口诀：左加右减、上加下减,中考重难点突破)二次函数的图象及性质【例1】(2016泰安中考)二次函数y＝ax2＋bx＋c的图象如图所示，那么一次函数y＝ax＋b的图象大致是( ),A),B),C) ,D) 【解析】∵y＝ax2＋bx＋c的图象的开口向上，∴a>0，∵对称轴在y轴的左侧，∴b>0，∴一次函数y＝ax＋b的图象经过一，二，三象限．故选A.【学生解答】A1．(2016益阳中考)关于抛物线y＝x2－2x＋1，下列说法错误的是( D)A．开口向上B．与x轴有两个重合的交点C．对称轴是直线x＝1D．当x>1时，y随x的增大而减小抛物线y＝ax2＋bx＋c(a≠0)的图象与a，b，c的关系【例2】(2016达州中考)如图，已知二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴交于点A(－1，0)，与y轴的交点B在(0，－2)和(0，－1)之间(不包括这两点)，对称轴为直线x＝1，下列结论：①abc>0；②4a＋2b＋c>0；③4ac－b 2<8a ；④13<a<23；⑤b>c.其中含所有正确结论的选项是( )A ．①③B ．①③④C ．②④⑤D ．①③④⑤【解析】①∵函数开口方向向上，∴a>0；∵对称轴在原点右侧，∴ab 异号，∵抛物线与y 轴交点在y 轴负半轴，∴c<0，∴abc>0，故①正确；②∵图象与x 轴交于点A(－1，0)，对称轴为直线x ＝1，∴图象与x 轴的另一个交点为(3，0)，∴当x ＝2时，y<0，∴4a ＋2b ＋c<0，故②错误；③∵图象与x 轴交于点A(－1，0)，∴当x＝－1时，y ＝(－1)2a ＋b×(－1)＋c ＝0，∴a －b ＋c ＝0，即a ＝b －c ，c ＝b －a ，∵对称轴为直线x ＝1，∴－b 2a＝1，即b ＝－2a ，∴c ＝b －a ＝(－2a)－a ＝－3a ，∴4ac －b 2＝4·a·(－3a)－(－2a)2＝－16a 2<0，∵8a>0，∴4ac －b 2<8a.故③正确；④∵图象与y 轴的交点B 在(0，－2)和(0，－1)之间，∴－2<c<－1，∴－2<－3a<－1，∴23>a>13；故④正确；⑤∵a>0，∴b －c>0，即b>c ；故⑤正确；故选D . 【学生解答】D2．(2016烟台中考)二次函数y ＝ax 2＋bx ＋c 的图象如图所示，下列结论：①4ac<b 2；②a＋c>b ；③2a＋b>0.其中正确的有( B )A ．①②B ．①③C ．②③D ．①②③(第2题图)(第3题图)3．(2016兰州中考)二次函数y＝ax2＋bx＋c的图象如图所示，对称轴是直线x＝－1，有以下结论：①abc>0；②4ac<b2；③2a＋b＝0；④a－b＋c>2.其中正确的结论的个数是( C)A．1个B．2个C．3个D．4个二次函数解析式的确定【例3】(2016承德二中模拟)如图，已知二次函数y＝ax2＋bx＋c的图象过A(2，0)，B(0，－1)和C(4，5)三点．(1)求二次函数的解析式；(2)设二次函数的图象与x 轴的另一个交点为D ，求点D 的坐标；(3)在同一坐标系中画出直线y ＝x ＋1，并写出当x 在什么范围内时，一次函数的值大于二次函数的值．【解析】(1)根据二次函数y ＝ax 2＋bx ＋c 的图象过A(2，0)，B(0，－1)和C(4，5)三点，代入得出关于a ，b ，c 的三元一次方程组，求得a ，b ，c ，从而得出二次函数的解析式；(2)令y ＝0，解一元二次方程，求得x 的值，从而得出与x 轴的另一个交点坐标； (3)画出图象，再根据图象直接得出答案．【学生解答】(1)∵二次函数y ＝ax 2＋bx ＋c 的图象过A(2，0)，B(0，－1)和C(4，5)三点，∴⎩⎪⎨⎪⎧4a ＋2b ＋c ＝0，c ＝－1，16a ＋4b ＋c ＝5，∴a ＝12，b ＝－12，c ＝－1，∴二次函数的解析式为y ＝12x 2－12x －1；(2)当y ＝0时，得12x 2－12x －1＝0，解得x 1＝2，x 2＝－1，∵点A 的坐标为(2，0)，∴点D 坐标为(－1，0)；(3)图象如图，当一次函数的值大于二次函数的值时，x 的取值范围是－1＜x ＜4.4．(2016邯郸二十三中模拟)已知二次函数y ＝x 2－4x ＋3.(1)用配方法求其函数图象的顶点C 的坐标，并描述该函数的函数值随自变量的增减而增减的情况； (2)求函数图象与x 轴的交点A ，B 的坐标，及△ABC 的面积．解：(1)y ＝x 2－4x ＋3＝(x －2)2－1. ∴其函数的顶点C 的坐标为(2，－1)． ∴当x<2时，y 随x 的增大而减小；当x>2时，y 随x 的增大而增大．(2)令y ＝0，则x 2－4x ＋3＝0，解得x 1＝1，x 2＝3. ∴当点A 在点B 左侧时，A(1，0)，B(3，0)； 当点A 在点B 右侧时，A(3，0)，B(1，0)．∴AB ＝|1－3|＝2.过点C 作CD⊥x 轴于D ，则△ABC 的面积＝12AB ·CD ＝12×2×1＝1.,中考备考方略)1．(2015兰州中考)在下列二次函数中，其图象的对称轴为直线x ＝－2的是( A )A ．y ＝(x ＋2)2B ．y ＝2x 2－2C ．y ＝－2x 2－2D ．y ＝2(x －2)22．(2016成都中考)二次函数y ＝2x 2－3的图象是一条抛物线，下列关于该抛物线的说法，正确的是( D ) A ．抛物线开口向下 B ．抛物线经过点(2，3)C ．抛物线的对称轴是直线x ＝1D ．抛物线与x 轴有两个交点3．(2016石家庄二十八中二模)二次函数y ＝x 2－2x ＋4化为y ＝a(x －h)2＋k 的形式，下列正确的是( B ) A ．y ＝(x －1)2＋2 B ．y ＝(x －1)2＋3 C ．y ＝(x －2)2＋2 D ．y ＝(x －2)2＋44．(2016滨州中考)抛物线y ＝2x 2－22x ＋1与坐标轴的交点个数是( C ) A ．0个 B ．1个 C ．2个 D ．3个5．(2016天津中考)已知二次函数y ＝(x －h)2＋1(h 为常数)，在自变量x 的值满足1≤x≤3的情况下，与其对应的函数值y 的最小值为5，则h 的值为( B )A ．1或－5B ．－1或5C ．1或－3D ．1或36．(2016黄石中考)以x 为自变量的二次函数y ＝x 2－2(b －2)x ＋b 2－1的图象不经过第三象限，则实数b 的取值范围是( A )A ．b ≥54B ．b ≥1或b≤－1C ．b ≥2D ．1≤b ≤27．(2016河南中考)已知A(0，3)，B(2，3)是抛物线y ＝－x 2＋bx ＋c 上两点，该抛物线的顶点坐标是__(1，4)__．8．(2016龙东中考)如图，二次函数y ＝(x ＋2)2＋m 的图象与y 轴交于点C ，点B 在抛物线上，且与点C 关于抛物线的对称轴对称，已知一次函数y ＝kx ＋b 的图象经过该二次函数图象上的点A(－1，0)及点B.(1)求二次函数与一次函数的解析式；(2)根据图象，写出满足(x ＋2)2＋m≥kx＋b 的x 的取值范围．解：(1)由题意，得(－1＋2)2＋m ＝0.∴m＝－1.二次函数的解析式为y ＝(x ＋2)2－1，即y ＝x 2＋4x ＋3.∴C(0，3)，∴B(－4，3)． ∵y ＝kx ＋b 经过点A ，B. ∴⎩⎪⎨⎪⎧－4k ＋b ＝3，－k ＋b ＝0，解得⎩⎪⎨⎪⎧k ＝－1，b ＝－1， ∴一次函数解析式为y ＝－x －1；(2)满足(x ＋2)2＋m≥kx＋b 的x 的取值范围为x≤－4或x≥－1.9．(2016滨州中考)在平面直角坐标系中，把一条抛物线先向上平移3个单位长度，然后绕原点旋转180°得到抛物线y ＝x 2＋5x ＋6，则原抛物线的解析式是( A )A ．y ＝－⎝ ⎛⎭⎪⎫x －522－114B ．y ＝－⎝ ⎛⎭⎪⎫x ＋522－114C ．y ＝－⎝ ⎛⎭⎪⎫x －522－14D ．y ＝－⎝ ⎛⎭⎪⎫x ＋522＋1410．(2016龙岩中考)已知抛物线y ＝ax 2＋bx ＋c 的图象如图所示，则|a －b ＋c|＋|2a ＋b|＝( D ) A ．a ＋b B ．a －2b C ．a －b D ．3a11．(2016随州中考)二次函数y ＝ax 2＋bx ＋c(a≠0)的部分图象如图所示，图象过点(－1，0)，对称轴为直线x ＝2，下列结论：①4a＋b ＝0；②9a＋c>3b ；③8a＋7b ＋2c>0；④若点A(－3，y 1)，点B ⎝ ⎛⎭⎪⎫－12，y 2，点C ⎝ ⎛⎭⎪⎫72，y 3在该函数图象上，则y 1<y 3<y 2；⑤若方程a(x ＋1)(x －5)＝－3的两根为x 1和x 2，且x 1<x 2，则x 1<－1<5<x 2，其中正确的结论有( B )A ．2个B ．3个C ．4个D ．5个12．(2016石家庄四十一中一模)如图，将抛物线l ：y ＝ax 2－2x ＋a 2－4(a 为常数)向左并向上平移，使顶点Q 的对应点Q′，抛物线l 与x 轴的右交点P 的对应点P′分别在两坐标轴上，则抛物线l 与x 轴的左交点E 的对应点的坐标为( A )A ．(－1，12) B ．(0，0)C ．(－12，1)D ．(－12，0)13．(2016秦皇岛二模)如图，在等腰△ABC 中，AB ＝AC ＝4 cm ，∠B ＝30°，点P 从点B 出发，以 3 cm /s 的速度沿BC 方向运动到点C 停止，同时点Q 从点B 出发，以1 cm /s 的速度沿BA —AC 方向运动到点C 停止，若△BPQ 的面积为y(cm 2)，运动时间为x(s )，则下列最能反映y 与x 之间函数关系的图象是( D ),A),B),C),D)14．(2016原创)如图为二次函数y＝ax2＋bx＋c(a≠0)的图象，则下列说法：①a＞0；②2a＋b＝0；③a＋b ＋c＞0；④当－1＜x＜3时，y＞0.其中正确结论的个数为( C)A．1个B．2个C．3个D．4个15．(2016菏泽中考)如图，一段抛物线：y＝－x(x－2)(0≤x≤2)记为C1，它与x轴交于两点O，A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；…如此进行下去，直至得到C6，若点P(11，m)在第6段抛物线C 6上，则m ＝__－1__．16．(2016安顺中考)如图，抛物线y ＝ax 2＋bx ＋52与直线AB 交于点A(－1，0)，B(4，52)．点D 是抛物线A ，B 两点间部分上的一个动点(不与点A ，B 重合)，直线CD 与y 轴平行，交直线AB 于点C ，连接AD ，BD.(1)求抛物线的解析式；(2)设点D 的横坐标为m ，△ADB 的面积为S ，求S 关于m 的函数关系式，并求出当S 取最大值时的点C 的坐标．解：(1)y ＝－12x 2＋2x ＋52；(2)设直线AB 为：y ＝kx ＋b ，则有⎩⎪⎨⎪⎧－k ＋b ＝0，4k ＋b ＝52.解得⎩⎪⎨⎪⎧k ＝12，b ＝12. ∴y ＝12x ＋12.则：D(m ，－12m 2＋2m ＋52)，C(m ，12m ＋12)，CD ＝(－12m 2＋2m ＋52)－(12m ＋12)＝－12m 2＋32m ＋2.∴S ＝12(m ＋1)·CD＋12(4－m)·CD＝12×5×CD ＝12×5×(－12m 2＋32m ＋2)＝－54m 2＋154m ＋5.∵－54＜0，∴当m ＝32时，S 有最大值．当m ＝32时，12m ＋12＝12×32＋12＝54.∴点C(32，54)．。

第三章函数第一节函数及其图象【考点1】平面直角坐标系及点的坐标1. 在平面内两条且有公共原点的数轴组成了平面直角坐标系。

2. 建立了平面直角坐标系的平面称为坐标平面。

3.坐标平面内每一个点P都对应着一个坐标x和一个坐标y，我们称一对有序实数P(x，y)，即点P的坐标。

4. 平面直角坐标系中点的特征【考点2】函数的有关概念及其表达式1. 变量：某一变化的过程中可以取不同数值的量叫做变量。

2. 常量：某一变化的过程中保持相同数值的量叫做常量。

3. 函数：在某一变化的过程中有两个量x和y，如果对于x的每一个值，y都有的值与它对应，那么称y是x的函数，其中x是，y是因变量。

4. 函数的表示方法有：、、。

在解决一些与函数有关的问题时，有时可以同时用两种或两种以上的方法来表示函数。

5. 画函数图象的一般步骤：列表、、。

【考点3】函数自变量的取值范围与函数值【中考试题精编】 1. 在函数中3-x =y ，自变量x 的取值范围是 ( )A. x ≠3B. x ＞3C. x ＜3D. x ≥32. 王芳同学为参加学校组织的科技知识竞赛，她周末到新华书店购买资料，如图是王芳离家的距离与时间的函数关系图象，若黑点表示王芳家的位置，则王芳走的路线可能是（ ）A. B. C. D.3. 函数1-x 2=y 中，自变量的取值范围是 。

4. 在函数x x y +-=31中，自变量x 的取值范围是 .5. 根据图中的程序，当输入x=2时，输出结果是 。

第二节 一次函数【考点1】一次函数的概念如果y=kx+b (k,b 为常数，且 )，那么y 叫做x 的一次函数。

当b=0时，也就是y=kx(k ≠0)，这时称y 是x 的正比例函数。

【考点2】一次函数的图象和性质 的增大而减小【考点3】一次函数与一次方程和一次不等式的关系一次函数y=kx+b (k,b 为常数，k ≠0) （1）当y=0时，一元一次方程kx+b=0(2) 当y ＞0或y ＜0时，一元一次不等式kx+b ＞0或kx+b ＜0【提示】当一次函数中的一个变量的值确定时，可用一元一次方程确定另一个变量的值；当 已知一次函数中的一个变量取值的范围时，可用一元一次不等式（组）确定另一个变量的取值。

二次函数知识点总结及相关典型题目第一部份 基础知识1.概念：一样地，若是c b a c bx ax y ,,(2++=是常数，)0≠a ，那么y 叫做x 的二次函数.2.二次函数2ax y =的性质（1）抛物线2ax y =的极点是坐标原点，对称轴是y 轴. （2）函数2ax y =的图像与a 的符号关系.①当0>a 时⇔抛物线开口向上⇔极点为其最低点；②当0<a 时⇔抛物线开口向下⇔极点为其最高点.（3）极点是坐标原点，对称轴是y 轴的抛物线的解析式形式为2ax y =）（0≠a .3.二次函数 c bx ax y ++=2的图像是对称轴平行于（包括重合）y 轴的抛物线.4.二次函数c bx ax y ++=2用配方式可化成：()k h x a y +-=2的形式，其中ab ac k a b h 4422-=-=，.5.二次函数由特殊到一样，可分为以下几种形式：①2ax y =；②k ax y +=2；③()2h x a y -=；④()k h x a y +-=2；⑤c bx ax y ++=2.6.抛物线的三要素：开口方向、对称轴、极点.①a 的符号决定抛物线的开口方向：当0>a 时，开口向上；当0<a 时，开口向下；a 相等，抛物线的开口大小、形状相同.②平行于y 轴（或重合）的直线记作h x =.专门地，y 轴记作直线0=x .7.极点决定抛物线的位置.几个不同的二次函数，若是二次项系数a 相同，那么抛物线的开口方向、开口大小完全相同，只是极点的位置不同. 8.求抛物线的极点、对称轴的方式（1）公式法：a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=，∴极点是），（a b ac a b 4422--，对称轴是直线abx 2-=. （2）配方式：运用配方的方式，将抛物线的解析式化为()k h x a y +-=2的形式，取得极点为(h ,k)，对称轴是直线h x =.（3）运用抛物线的对称性：由于抛物线是以对称轴为轴的轴对称图形，因此对称轴的连线的垂直平分线是抛物线的对称轴，对称轴与抛物线的交点是极点.用配方式求得的极点，再用公式法或对称性进行验证，才能做到万无一失. 9.抛物线c bx ax y ++=2中，c b a ,,的作用（1）a 决定开口方向及开口大小，这与2ax y =中的a 完全一样.（2）b 和a 一起决定抛物线对称轴的位置.由于抛物线c bx ax y ++=2的对称轴是直线a b x 2-=，故：①0=b 时，对称轴为y 轴；②0>a b （即a 、b 同号）时，对称轴在y 轴左侧；③0<ab （即a 、b 异号）时，对称轴在y 轴右边.（3）c 的大小决定抛物线c bx ax y ++=2与y 轴交点的位置.当0=x 时，c y =，∴抛物线c bx ax y ++=2与y 轴有且只有一个交点（0，c ）： ①0=c ，抛物线通过原点; ②0>c ,与y 轴交于正半轴；③0<c ,与y 轴交于负半轴. 以上三点中，当结论和条件互换时，仍成立.如抛物线的对称轴在y 轴右边，那么 0<ab. 10.几种特殊的二次函数的图像特点如下：11.用待定系数法求二次函数的解析式（1）一样式：c bx ax y ++=2.已知图像上三点或三对x 、y 的值，通常选择一样式. （2）极点式：()k h x a y +-=2.已知图像的极点或对称轴，通常选择极点式.（3）交点式：已知图像与x 轴的交点坐标1x 、2x ，通常选用交点式：()()21x x x x a y --=. 12.直线与抛物线的交点（1）y 轴与抛物线c bx ax y ++=2得交点为(0, c ).（2）与y 轴平行的直线h x =与抛物线c bx ax y ++=2有且只有一个交点(h ,c bh ah ++2).（3）抛物线与x 轴的交点二次函数c bx ax y ++=2的图像与x 轴的两个交点的横坐标1x 、2x ，是对应一元二次方程02=++c bx ax 的两个实数根.抛物线与x 轴的交点情形能够由对应的一元二次方程的根的判别式判定：①有两个交点⇔0>∆⇔抛物线与x 轴相交；②有一个交点（极点在x 轴上）⇔0=∆⇔抛物线与x 轴相切； ③没有交点⇔0<∆⇔抛物线与x 轴相离. （4）平行于x 轴的直线与抛物线的交点同（3）一样可能有0个交点、1个交点、2个交点.当有2个交点时，两交点的纵坐标相等，设纵坐标为k ，那么横坐标是k c bx ax =++2的两个实数根.（5）一次函数()0≠+=k n kx y 的图像l 与二次函数()02≠++=a c bx ax y 的图像G 的交点，由方程组cbx ax y n kx y ++=+=2的解的数量来确信：①方程组有两组不同的解时⇔l 与G 有两个交点; ②方程组只有一组解时⇔l 与G 只有一个交点；③方程组无解时⇔l 与G 没有交点.（6）抛物线与x 轴两交点之间的距离：假设抛物线c bx ax y ++=2与x 轴两交点为()()0021，，，x B x A ，由于1x 、2x 是方程02=++c bx ax 的两个根，故ac x x a b x x =⋅-=+2121,()()a a acb ac a b x x x x x x x x AB ∆=-=-⎪⎭⎫⎝⎛-=--=-=-=444222122122121第二部份 典型习题１.抛物线y ＝x 2＋2x －2的极点坐标是 （ D ）A.（2，－2）B.（1，－2）C.（1，－3）D.（－1，－3） ２.已知二次函数c bx ax y ++=2的图象如下图，那么以下结论正确的选项是（ C ）Ａ．ab ＞0，c ＞0 Ｂ．ab ＞0，c ＜0 Ｃ．ab ＜0，c ＞0 Ｄ．ab ＜0，c ＜0第２,３题图 第4题图３.二次函数c bx ax y ＋＋＝2的图象如下图，那么以下结论正确的选项是（ Ｄ ） A ．a ＞0，b ＜0，c ＞0 B ．a ＜0，b ＜0，c ＞0 C ．a ＜0，b ＞0，c ＜0 D ．a ＜0，b ＞0，c ＞0 ４.如图，已知中，BC=8，BC 上的高，D 为BC 上一点，，交AB 于点E ，交AC 于点F （EF只是A 、B ），设E 到BC 的距离为，那么的面积关于的函数的图象大致为（ Ｄ ）2482,484EF xEF x y x x -=⇒=-∴=-+ ５.抛物线322--=x x y 与x 轴别离交于A 、B 两点，那么AB 的长为 4 ．6.已知二次函数11)(2k 2－－＋＝x kx y 与x 轴交点的横坐标为1x 、2x （21x x ＜），那么关于以下结论：①当x ＝－2时，y ＝1；②当2x x ＞时，y ＞0；③方程011)(22＝－＋-x k kx 有两个不相等的实数根1x 、2x ；④11-＜x ，12＞－x ；⑤21x x k－，其中所有正确的结论是 ①③④ （只需填写序号）．7.已知直线()02≠+-=b b x y 与x 轴交于点A ，与y 轴交于点B ；一抛物线的解析式为()c x b x y ++-=102.（1）假设该抛物线过点B ，且它的极点P 在直线b x y +-=2上，试确信这条抛物线的解析式；（2）过点B 作直线BC ⊥AB 交x 轴交于点C ，假设抛物线的对称轴恰好于C 点，试确信直线b x y +-=2的解析式.解：（1）102-=x y 或642--=x x y将0)b （，代入，得c b =.极点坐标为21016100(,)24b b b +++-，由题意得21016100224b b b b +++-⨯+=-，解得1210,6b b =-=-.（2）22--=x y8.有一个运算装置，当输入值为x 时，其输出值为y ，且y 是x 的二次函数，已知输入值为2-,0,1时, 相应的输出值别离为5,3-,4-．第9题（1）求此二次函数的解析式；（2）在所给的坐标系中画出那个二次函数的图象,并依照图象写出当输出值y 为正数时输入值x 的取值范围. 解：（1）设所求二次函数的解析式为c bx ax y ++=2,则⎪⎪⎩⎪⎪⎨⎧-=++-=+⋅+⋅=+-+-43005)2()2(22c b a c b a c b a ,即⎪⎩⎪⎨⎧-=+=--=1423b a b a c ,解得⎪⎩⎪⎨⎧-=-==321c b a 故所求的解析式为:322--=x x y . （2)函数图象如下图.由图象可得，当输出值y 为正数时， 输入值x 的取值范围是1-<x 或3>x ．9.某生物爱好小组在四天的实验研究中发觉：骆驼的体温会随外部环境温度的转变而转变，而且在这四天中每日夜的体温转变情形相同．他们将一头骆驼前两日夜的体温转变情形绘制成以下图．请依照图象回答： ⑴第一天中，在什么时刻范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多少时刻?⑵第三天12时这头骆驼的体温是多少? ⑶爱好小组又在研究中发觉，图中10时到 22时的曲线是抛物线，求该抛物线的解 析式．解：⑴第一天中，从4时到16时这头骆驼的体温是上升的它的体温从最低上升到最高需要12小时 ⑵第三天12时这头骆驼的体温是39℃⑶()22102421612≤≤++-=x x x y 10.已知抛物线4)334(2+++=x a ax y 与x 轴交于A 、B 两点，与y 轴交于点C ．是不是存在实数a ，使得 △ABC 为直角三角形．假设存在，请求出a 的值；假设不存在，请说明理由．解：依题意，得点C 的坐标为（0，4）．设点A 、B 的坐标别离为（1x ，0），（2x ，0），由04)334(2=+++x a ax ，解得 31-=x ，ax 342-=． ∴ 点A 、B 的坐标别离为（-3，0），（a34-，0）． ∴ |334|+-=aAB ，522=+=OC AO AC ， =+=22OC BO BC 224|34|+-a． ∴ 9891693432916|334|2222+-=+⨯⨯-=+-=aa a a a AB ， 252=AC ，1691622+=a BC ．〈ⅰ〉当222BC AC AB +=时，∠ACB ＝90°． 由222BC AC AB +=，得)16916(259891622++=+-a a a ． 解得 41-=a ．∴ 当41-=a 时，点B 的坐标为（316，0），96252=AB ，252=AC ，94002=BC ．于是222BC AC AB +=． ∴ 当41-=a 时，△ABC 为直角三角形． 〈ⅱ〉当222BC AB AC +=时，∠ABC ＝90°． 由222BC AB AC +=，得)16916()98916(2522+++-=aa a ． 解得 94=a ． 当94=a 时，3943434-=⨯=-a ，点B （-3，0）与点A 重合，不合题意．〈ⅲ〉当222AB AC BC +=时，∠BAC ＝90°． 由222AB AC BC +=，得)98916(251691622+-+=+aa a ． 解得 94=a ．不合题意． 综合〈ⅰ〉、〈ⅱ〉、〈ⅲ〉，当41-=a 时，△ABC 为直角三角形． 11.已知抛物线y ＝－x 2＋mx －m ＋2.（1）假设抛物线与x 轴的两个交点A 、B 别离在原点的双侧，而且AB 5m 的值；（2）设C 为抛物线与y 轴的交点，假设抛物线上存在关于原点对称的两点M 、N ，而且 △MNC 的面积等于27，试求m 的值.解: (1)Ａ（x 1，0）,B(x 2，0) . 那么x 1 ，x 2是方程 x 2－mx ＋m －2＝0的两根. ∵x 1 ＋ x 2 ＝m , x 1·x 2 =m －2 ＜0 即m ＜2 ;又AB ＝∣x 1 — x 2121245x x x x -=2（+）∴m 2－4m ＋3=0 .解得：m=1或m=3(舍去) , ∴m 的值为1 . （2）M(a ，b)，那么N(－a ，－b) . ∵M 、N 是抛物线上的两点,∴222,2.a ma m b a ma m b ⎧-+-+=⎪⎨---+=-⎪⎩①②①＋②得：－2a 2－2m ＋4＝0 . ∴a 2＝－m ＋2 . ∴当m ＜2时，才存在知足条件中的两点M 、N. ∴2a m =-这时M 、N 到y 2m -又点C 坐标为（0，2－m ）,而S △M N C = 27 , ∴2×12×（2－m 2m -∴解得m=－7 .12.已知：抛物线t ax ax y ＋＋＝42与x 轴的一个交点为A （－1，0）． （1）求抛物线与x 轴的另一个交点B 的坐标；（2）D 是抛物线与y 轴的交点，C 是抛物线上的一点，且以AB 为一底的梯形ABCD 的面积为9，求此抛物线的解析式；（3）E 是第二象限内到x 轴、y 轴的距离的比为5∶2的点，若是点E 在（2）中的抛物线上，且它与点A 在此抛物线对称轴的同侧，问：在抛物线的对称轴上是不是存在点P ，使△APE 的周长最小?假设存在，求出点P 的坐标；假设不存在，请说明理由． 解法一：（1）依题意，抛物线的对称轴为x ＝－2． ∵ 抛物线与x 轴的一个交点为A （－1，0），∴ 由抛物线的对称性，可得抛物线与x 轴的另一个交点B 的坐标为（－3，0）．NMCx y O（2）∵ 抛物线t ax ax y ＋＋＝42与x 轴的一个交点为A （－1， 0），∴ 0)1(4)1(2＝＋－＋－t a a ．∴ t ＝3a ．∴ a ax ax y 342＋＋＝． ∴ D （0，3a ）．∴ 梯形ABCD 中，AB ∥CD ，且点C 在抛物线a ax ax y 342＋＋＝ 上， ∵ C （－4，3a ）．∴ AB ＝2，CD ＝4． ∵ 梯形ABCD 的面积为9，∴ 9)(21＝OD CD AB ⋅+．∴ 93)42(21＝＋a ．∴ a ±1．∴ 所求抛物线的解析式为342＋＋＝x x y 或342---ax x y ＝． （3）设点E 坐标为（0x ，0y ）.依题意，00＜x ，00＜y ， 且2500＝x y ．∴ 0025x y ＝－．①设点E 在抛物线342＋＋＝x x y 上，∴340200＋＋＝x x y ．解方程组⎪⎩⎪⎨⎧34,25020000＋＋＝＝－x x y x y 得⎩⎨⎧-；＝，＝15600y x ⎪⎪⎩⎪⎪⎨⎧'-'．＝，＝452100y x ∵ 点E 与点A 在对称轴x ＝－2的同侧，∴ 点E 坐标为（21-，45）． 设在抛物线的对称轴x ＝－2上存在一点P ，使△APE 的周长最小． ∵ AE 长为定值，∴ 要使△APE 的周长最小，只须PA ＋PE 最小． ∴ 点A 关于对称轴x ＝－2的对称点是B （－3，0）， ∴ 由几何知识可知，P 是直线BE 与对称轴x ＝－2的交点． 设过点E 、B 的直线的解析式为n mx y ＋＝，∴ ⎪⎩⎪⎨⎧-.03,4521＝＋－＝＋n m n m 解得⎪⎪⎩⎪⎪⎨⎧.23,21＝＝n m ∴ 直线BE 的解析式为2321＋＝x y ．∴ 把x ＝－2代入上式，得21＝y ． ∴ 点P 坐标为（－2，21）． ②设点E 在抛物线342---x x y ＝上，∴ 340200---x x y ＝．解方程组⎪⎩⎪⎨⎧---.34,25020000x x y x y ＝＝－ 消去0y ，得03x 23x 020＝＋+． ∴ △＜0 . ∴ 此方程无实数根． 综上，在抛物线的对称轴上存在点P （－2，21），使△APE 的周长最小． 解法二：（1）∵ 抛物线t ax ax y ＋＋＝42与x 轴的一个交点为A （－1，0），∴ 0)1(4)1(2＝＋－＋－t a a ．∴ t ＝3a ．∴ a ax ax y 342＋＋＝．令 y ＝0，即0342＝＋＋a ax ax ．解得 11＝－x ，32＝－x ． ∴ 抛物线与x 轴的另一个交点B 的坐标为（－3，0）．（2）由a ax ax y 342＋＋＝，得D （0，3a ）． ∵ 梯形ABCD 中，AB ∥CD ，且点C 在抛物线a ax ax y 342＋＋＝上，∴ C （－4，3a ）．∴ AB ＝2，CD ＝4． ∵ 梯形ABCD 的面积为9，∴ 9)(21＝＋OD CD AB ⋅．解得OD ＝3． ∴ 33＝a ．∴ a ±1．∴ 所求抛物线的解析式为342＋＋＝x x y 或342－－＝－x x y ．（3）同解法一得，P 是直线BE 与对称轴x ＝－2的交点． ∴ 如图，过点E 作EQ ⊥x 轴于点Q ．设对称轴与x 轴的交点为F ．由PF ∥EQ ，可得EQ PF BQ BF ＝．∴ 45251PF ＝．∴ 21＝PF ．∴ 点P 坐标为（－2，21）．以下同解法一．13.已知二次函数的图象如下图．（1）求二次函数的解析式及抛物线极点M 的坐标．（2）假设点N 为线段BM 上的一点，过点N 作x 轴的垂线，垂足为点Q ．当点N 在线段BM 上运动时（点N 不与点B ，点M 重合），设NQ 的长为l ，四边形NQAC 的面积为S ，求S 与t 之间的函数关系式及自变量t 的取值范围；（3）在对称轴右边的抛物线上是不是存在点P ，使△PAC 为直角三角形?假设存在，求出所有符合条件的点P 的坐标；假设不存在，请说明理由；（4）将△OAC 补成矩形，使△OAC 的两个极点成为矩形一边的两个极点，第三个极点落在矩形这一边的对边上，试直接写出矩形的未知的极点坐标（不需要计算进程）．解：（1）设抛物线的解析式)2)(1(-+=x x a y ，∴ )2(12-⨯⨯=-a ．∴ 1=a ．∴ 22--=x x y ． 其极点M 的坐标是⎪⎭⎫ ⎝⎛-4921，． （2）设线段BM 所在的直线的解析式为b kx y +=，点N 的坐标为N （t ，h ），∴ ⎪⎩⎪⎨⎧+=-+=.214920b k b k ，．解得23=k ，3-=b ． ∴ 线段BM 所在的直线的解析式为323-=x y ． ∴ 323-=t h ，其中221<<t ．∴ t t s )3322(212121-++⨯⨯=121432+-=t t ． ∴ s 与t 间的函数关系式是121432+-=t t S ，自变量t 的取值范围是221<<t ． （3）存在符合条件的点P ，且坐标是1P ⎪⎭⎫ ⎝⎛4725，，⎪⎭⎫ ⎝⎛-45232，P ． 设点P 的坐标为P )(n m ，，那么22--=m m n ． 222)1(n m PA ++=，5)2(2222=++=AC n m PC ，．分以下几种情形讨论：i ）假设∠PAC ＝90°，那么222AC PA PC +=．∴ ⎪⎩⎪⎨⎧+++=++--=.5)1()2(222222n m n m m m n ， 解得：251=m ，12-=m （舍去）． ∴ 点⎪⎭⎫ ⎝⎛47251，P ． ii ）假设∠PCA ＝90°，那么222AC PC PA +=．∴ ⎪⎩⎪⎨⎧+++=++--=.5)2()1(222222n m n m m m n ，解得：02343==m m ，（舍去）．∴ 点⎪⎭⎫ ⎝⎛45232，－P ． iii ）由图象观看得，当点P 在对称轴右边时，AC PA >，因此边AC 的对角∠APC 不可能是直角．（4）以点O ，点A （或点O ，点C ）为矩形的两个极点，第三个极点落在矩形这边OA （或边OC ）的对边上，如图a ，现在未知极点坐标是点D （－1，－2），以点A ，点C 为矩形的两个极点，第三个极点落在矩形这一边AC 的对边上，如图b ，现在未知极点坐标是E ⎪⎭⎫⎝⎛-5251，，F ⎪⎭⎫ ⎝⎛-5854，．图a 图b14.已知二次函数22－＝ax y 的图象通过点（1，－1）．求那个二次函数的解析式，并判定该函数图象与x 轴的交点的个数．解：依照题意，得a －2＝－1.∴ a ＝1． ∴ 那个二次函数解析式是22-x y ＝．因为那个二次函数图象的开口向上，极点坐标是（0，－2），因此该函数图象与x 轴有两个交点．15.卢浦大桥拱形能够近似看做抛物线的一部份．在大桥截面1∶11000的比例图上，跨度AB ＝5 cm ，拱高OC ＝0.9 cm ，线段DE 表示大桥拱内桥长，DE ∥AB ，如图（1）．在比例图上，以直线AB 为x 轴，抛物线的对称轴为y 轴，以1 cm 作为数轴的单位长度，成立平面直角坐标系，如图（2）．（1）求出图（2）上以这一部份抛物线为图象的函数解析式，写出函数概念域； （2）若是DE 与AB 的距离OM ＝0.45 cm ，求卢浦大桥拱内实际桥长（备用数据：4.12≈，计算结果精准到1米）．解：（1）由于极点C 在y 轴上，因此设以这部份抛物线为图象的函数解析式为1092＋＝ax y ．因为点A （25-，0）（或B （25，0））在抛物线上， 因此109)25(02＋＝-⋅a ，得12518＝－a ．因此所求函数解析式为)2525(109125182≤≤-x x y ＋＝－．（2）因为点D 、E 的纵坐标为209， 因此109125182092＋－x =，得245±＝x ． 因此点D 的坐标为（245－，209），点E 的坐标为（245，209）． 因此225)245(245＝－＝-DE ． 因此卢浦大桥拱内实际桥长为385227501.011000225≈⨯⨯＝（米）． 16.已知在平面直角坐标系内，O 为坐标原点，A 、B 是x 轴正半轴上的两点，点A 在点B 的左侧，如图．二次函数c bx ax y ＋＋＝2（a ≠0）的图象通过点A 、B ，与y 轴相交于点C ．（1）a 、c 的符号之间有何关系?（2）若是线段OC 的长度是线段OA 、OB 长度的比例中项，试证a 、c 互为倒数；（3）在（2）的条件下，若是b ＝－4，34＝AB ，求a 、c 的值．解:（1）a 、c 同号． 或当a ＞0时，c ＞0；当a ＜0时，c ＜0．（2）证明：设点A 的坐标为（1x ，0），点B 的坐标为（2x ，0），那么210x x ＜＜．∴ 1x OA =，2x OB =，c OC =．据题意，1x 、2x 是方程)0(02≠=a c bx ax ＋＋的两个根． ∴ ac x x =⋅21． 由题意，得2OC OB OA ＝⋅，即22c c a c＝＝． 因此当线段OC 长是线段OA 、OB 长的比例中项时，a 、c 互为倒数．（3）当4-=b 时，由（2）知，0421＞＝＝－＋a a b x x ，∴ a ＞0．解法一：AB ＝OB －OA ＝21221124)(x x x x x x -＋＝－，∴ aa ac a c a AB 32416)(4)4(22=-==－．∵ 34=AB ， ∴ 3432＝a ．得21=a ．∴ c ＝2. 解法二：由求根公式，a a a ac x 322416424164±-±-±＝＝＝， ∴ a x 321-＝，ax 322+＝． ∴ a a a x x OA OB AB 32323212＝－－＝－＝－＝+． ∵ 34＝AB ，∴ 3432＝a ，得21＝a ．∴ c ＝2． 17.如图，直线333+-=x y 别离与x 轴、y 轴交于点A 、B ，⊙E 通过原点O 及A 、B 两点． （1）C 是⊙E 上一点，连结BC 交OA 于点D ，假设∠COD ＝∠CBO ，求点A 、B 、C 的坐标；（2）求通过O 、C 、A 三点的抛物线的解析式：（3）假设延长BC 到P ，使DP ＝2，连结AP ，试判定直线PA 与⊙E 的位置关系，并说明理由．解：（1）连结EC 交x 轴于点N （如图）．∵ A 、B 是直线333+-=x y 别离与x 轴、y 轴的交点．∴ A （3，0），B )3,0(． 又∠COD ＝∠CBO ． ∴ ∠CBO ＝∠ABC ．∴ C 是的中点． ∴ EC ⊥OA ．∴ 232,2321====OB EN OA ON ． 连结OE ．∴ 3==OE EC ． ∴ 23=-=EN EC NC ．∴ C 点的坐标为（23,23-）． （2）设通过O 、C 、A 三点的抛物线的解析式为()3-=x ax y ．∵ C （23,23-）． ∴)323(2323-⋅=-a ．∴ 392=a ． ∴ x x y 8329322-=为所求． （3）∵ 33tan =∠BAO ， ∴ ∠BAO ＝30°，∠ABO ＝50°． 由（1）知∠OBD ＝∠ABD ．∴ ︒=︒⨯-∠=∠30602121ABO OBD ．∴ OD＝OB·tan30°－1．∴ DA＝2．∵∠ADC＝∠BDO＝60°，PD＝AD＝2．∴△ADP是等边三角形．∴∠DAP＝60°．∴∠BAP＝∠BAO＋∠DAP＝30°＋60°＝90°．即PA⊥AB．即直线PA是⊙E的切线．。

第三章函数及其图像课时 11.平面直角坐标系与函数的概念【考点链接】1.坐标平面内的点与 ______________ 一一对应．2.根据点所在位置填表（图）点的位置横坐标符号纵坐标符号第一象限第二象限第三象限第四象限3.x 轴上的点______坐标为0,y 轴上的点______坐标为0.4．各象限角平分线上的点的坐标特征⑴第一、三象限角平分线上的点，横、纵坐标。

⑵第二、四象限角平分线上的点，横、纵坐标。

5.P(x,y)关于x轴对称的点坐标为__________，关于y轴对称的点坐标为________，关于原点对称的点坐标为 ___________.以上特征可归纳为：⑴关于 x 轴对称的两点：横坐标相同，纵坐标；⑵关于 y 轴对称的两点：横坐标，纵坐标相同；⑶关于原点对称的两点：横、纵坐标均。

6.描点法画函数图象的一般步骤是__________、 __________ 、 __________ ．7.函数的三种表示方法分别是 __________ 、__________ 、__________ ．8.求函数自变量的取值范围时，首先要考虑自变量的取值必须使解析式有意义。

⑴自变量以整式形式出现，它的取值范围是；⑵自变量以分式形式出现，它的取值范围是；⑶自变量以根式形式出现，它的取值范围是；例如： y x 有意义，则自变量x 的取值范围是.y 1x 的取值范围是。

有意义，则自变量x【河北中考试题】的顶点上，且它们的各边与正方形ABCD 各边平行或垂直．若小正方形的边长为x ，且0x ≤ 10 ，阴影部分的面积为y ，则能反映y 与x之间函数关系的大致图象是（）xD y y y yA100100100100B C O10x x xO x图 4O10O 5 1010 A ． B ．C． D ．2.（ 2009 年， 2分）如图 6 所示的计算程序中，y 与 x 之间的函数关系输入 x 所对应的图象应为（）y y y4-2O x- 2 O x O 2x- 4- 4取相反数y4×2 O 2x＋4输出 yA B C D图 63.（ 2010 年， 2 分）一艘轮船在同一航线上往返于甲、乙两地．已知轮船在静水中的速度为15 km/h，水流速度为 5 km /h．轮船先从甲地顺水航行到乙地，在乙地停留一段时间后，又从乙地逆水航行返回到甲地．设轮船从甲地出发后所用时间为t（ h），航行的路程为s（ km），则 s 与 t 的函数图象大致是（）s s s sO t O t O t O tA B C D11．（2011）如图4，在长形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆住的侧面，刚好能组合成圆住.设矩形的长和宽分别为y 和 x，则 y 与 x 的函数图象大致是16．如图 9，梯形 ABCD中， AB∥ DC，DE⊥AB，CF⊥AB，且 AE = EF = FB = 5，DE = 12动点 P 从点 A 出发，沿折线 AD-DC-CB 以每秒 1 个单位长的速度运动到点 B 停止 . 设运动时间为 t 秒， y = S△EPF，则 y 与 t 的函数图象大致是课时 12.一次函数【考点链接】1．正比例函数的一般形式是__________ ．一次函数的一般形式是__________________.2.一次函数 y kx b 的图象是经过和两点的一条.3.求一次函数的解析式的方法是，其基本步骤是：⑴；⑵；⑶；⑷.4.一次函数 y kx b 的图象与性质k、b 的符号k＞ 0b＞ 0k＞0 b ＜ 0k＜ 0 b ＞ 0k＜ 0b＜ 0图像的大致位置经过象限第象限第象限第象限第象限性质y 随 x 的增大y 随 x的增大y 随 x 的增大y 随 x 的增大而而而而5.一次函数 y kx b 的性质k＞ 0直线上升y 随 x 的增大而；【河北中考试题】1. 2008 8 11l 1的解析表达式为y3x 3，且 l 1 与 x 轴交于点 D ，直线 l 2经过点 A ， B ，（ 年， 分）如图 ，直线直线l 1 ， l 2 交于点 C ．y（ 1）求点 D 的坐标；l 1l 2（ 2）求直线 l 2 的解析表达式；D 3（ 3）求 △ ADC 的面积；Ox3A （ 4， 0）（ 4）在直线 l 2 上存在异于点 C 的另一点 P ，使得2BC△ ADP 与 △ ADC 的面积相等，请直接写出点 P 的坐标． ．．图 112.（ 2009 年， 12 分） 某公司装修需用 A 型板材 240 块、 B 型板材 180 块， A 型板材规格是 60 cm ×30 cm ，B 型板材规格是 40 cm ×30 cm ．现只能购得规格是 150 cm ×30 cm 的标准板材． 一张标准板材尽可能多地裁出 A 型、 B 型板材，共有下列三种裁法： （图 15 是裁法一的裁剪示意图）裁法一裁法二裁法三A 型板材块数120B 型板材块数2m n设所购的标准板材全部裁完，其中按裁法一裁x 张、按裁法二裁y张、按裁法三裁z 张，且所裁出的 A 、B 两种型号的板材刚好够用．（ 1）上表中， m =，n =；（ 2）分别求出y 与 x 和 z 与 x 的函数关系式；（ 3）若用 Q 表示所购标准板材的张数，求Q 与 x 的函数关系式，并指出当 x 取何值时 Q 最小，此时按三种裁法各裁标准板材多少张？5．（2011）一次函数y=6x＋ 1 的图象不经过．．．A．第一象限B．第二象限C．第三象限 D ．第四象限24．（ 2011）（本小题满分9 分）已知 A、B 两地的路程为240 千米，某经销商每天都要用汽车或火车将x 吨保鲜品一次性由 A 地运往 B 地，受各种因素限制，下一周只能采用汽车和火车中的一种进行运输，且须提前预订.现在有货运收费项目及收费标准表，行驶路程S（千米）与行驶时间t（时）的函数图象（如图13中①），上周货运量折线统计图（如图13 中②）等信息如下：货运收费项目及收费标准表运输工具运输费单价冷藏单价固定费用元 /（吨 ?千米）元/（吨?时）元/次汽车25200火车 1.652280⑴汽车的速度为__________千米 /时，火车的速度为_________ 千米 /时；设每天用汽车和火车运输的总费用分别为y 汽（元）和 y 火（元），分别求 y 汽、y 火与 x 的函数关系式（不必写出x 的取值范围）及x 为何值时 y 汽＞y 火；（总费用 =运输费＋冷藏费＋固定费用）⑶请你从平均数、折线图走势两个角度分析，建议该经销商应提前下周预定哪种运输工具，才能使每天的运输总费用较省？26．（本小题满分 14 分）一透明的敞口正方体容器 ABCD - A′B′C′装D′有一些液体，棱 AB始终在水平桌面上，容器底部的倾斜角为（∠ CBE = α，如图 17-1所示）．探究如图 17-1，液面刚好过棱 CD，并与棱 BB′交于点Q，此时液体的形状为直三棱柱，其三视图及尺寸如图 17-2 所示．解决问题：（1）CQ与BE的位置关系是 ___________，BQ的长是 ____________dm；（2）求液体的体积；（参考算法：直棱柱体积 V液 =底面积 SBCQ×高 AB）33（ 3）求α的度数 .( 注： sin49 °＝ cos41°＝4， tan37°＝4)拓展在图 17-1 的基础上，以棱AB 为轴将容器向左或向右旋转，但不能使液体溢出，图 17-3 或图 17-4 是其正面示意图 . 若液面与棱 C′C或 CB交于点 P，设 PC = x，BQ = y. 分别就图 17-3 和图 17-4 求 y 与x的函数关系式，并写出相应的α的范围 .延伸在图 17-4 的基础上，于容器底部正中间位置，嵌入一平行于侧面的长方形隔板（厚度忽略不计），得到图 17-5，隔板高 NM = 1 dm， BM = CM，NM⊥BC. 继续向右缓慢旋转，当α= 60 °时，通过计算，判断溢出容器的液体能否达到 4 dm3.6、（ 2014）如图，直线 l 经过第二，三，四象限，l 的解析式是y=（ m-2） x+n，则 m 的取值范围则数轴上表示为（）A BDC26.（ 2014）（本小题满分 13 分）某景区的环形路是边长为800 米的正方形 ABCD ，如图，现有 1 号， 2 号两游览车分别从出口 A 和经典 C 同时出发， 1 号车顺时针， 2 号车逆时针沿环形路连续循环行驶，供游客随时乘车（上，下车的时间忽略不计），两车的速度均为200 米 /分。