【全国百强校】重庆市第八中学2018届高考适应性月考(六)数学(文)答案
- 格式:pdf
- 大小:207.33 KB
- 文档页数:7


文科数学参考答案·第1页(共7页)重庆市第八中学2018届高考适应性月考卷(六)文科数学参考答案一、选择题(本大题共12小题,每小题5分,共60分)题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C B C C A D C D B B A D 【解析】1.[22]M =-,,(04)N =,,(0][4)N =-∞+∞R ,, ,∴[20]M N =-R , ,故选C .2.由题知21i z =-,121i (1i)(12i)13ii 12i(12i)(12i)5z z +++-+===---+,故选B. 3.∵sin 22sin cos 0ααα=> ,∴sin tan 0cos ααα=>,故选C . 4.∵离心率e ==26a =,a =,故选C . 5.∵函数()f x 为R 上的奇函数,∴0(0)e 0f m =+=,解得1m =-,故1ln (ln 2)2f f ⎛⎫=- ⎪⎝⎭ln 2(ln 2)(e 1)1f =-=--=-,故选A .6.由等差数列的前n 项和性质知3S ,63S S -,96S S -成等差数列,又635S S =-,∴63S S -=36S -,∴96313S S S -=-,即9318S S =-,∴9318S S =-,故选D . 7.该几何体是由一个半圆锥和一个圆柱组合而成,2114ππ22233V ==半圆锥,2π2V = 圆柱 28π=,∴该几何体的体积为28π3,故选C . 8.记3名老年人,2名中年人和1名青年人分别为1A ,2A ,3A ,1B ,2B ,C ,则该随机试验的所有结果可记为12()A A ,,13()A A ,,11()A B ,,12()A B ,,1()A C ,,23()A A ,,21()A B ,,22()A B ,,2()A C ,,31()A B ,,32()A B ,,3()A C ,,12()B B ,,1()B C ,,2()B C ,,共15种,其中来自不同年龄层次的有11种,由古典概型知概率为1115,故选D .文科数学参考答案·第2页(共7页)9.由题意得()2sin(22)g x x ϕ=+,∴πππ2sin 222sin 212126g ϕϕ⎛⎫⎛⎫⎛⎫=⨯+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,即πsin 262ϕ⎛⎫+=⎪⎝⎭,又π04ϕ<<,∴ππ2π2663ϕ⎛⎫+∈ ⎪⎝⎭,,∴ππ263ϕ+=,解得π12ϕ=,π()2sin 26g x x ⎛⎫=+ ⎪⎝⎭∴,又πππ2sin 2012126g ⎡⎤⎛⎫⎛⎫-=⨯-+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,∴π012⎛⎫- ⎪⎝⎭是()g x 的一个对称中心,故选B .10.图中的程序框图是计算当2x =时,多项式234()032f x x x x x =+++-的值,∴(2)p f ==2-,故选B .11.设BC 的中点为D ,由32AO AB AC AD =+=,知外心与重心重合,则ABC △为等边三角形,而1BC =,∴111cos602AB AC =︒= ,故选A .12.由题知[()()]e 1x f x f x '+=,即(e ())1x f x '= ,∴e ()x f x x c =+(c 为常数),()e xx c f x +=,又(0)1f =,∴1c =,即1()e x x f x +=, ()ex xf x -'=∴.令()0f x '=,得0x =,当(0)x ∈-∞,时,()0f x '>,()f x 单增;当(0)x ∈+∞,时,()0f x '<,()f x 单减,且(1)0f -=,则()f x 的大致图象如图1所示,①12m =-,0n =时,()0f x =或1()2f x =,此时方程有3个不等实根;②1m n +=-时,()1f x =,即0x =恒满足方程;③0n <且1m n +>-时,对函数2()g t t mt n =++有(0)0g <,(1)0g >,()0g t =∴有两个不等的根1t ,2t ,且1(0)t ∈-∞,,2(01)t ∈,,此时,方程有三个不等的根,故①②③均正确,故选D .二、填空题(本大题共4小题,每小题5分,共20分)图1。
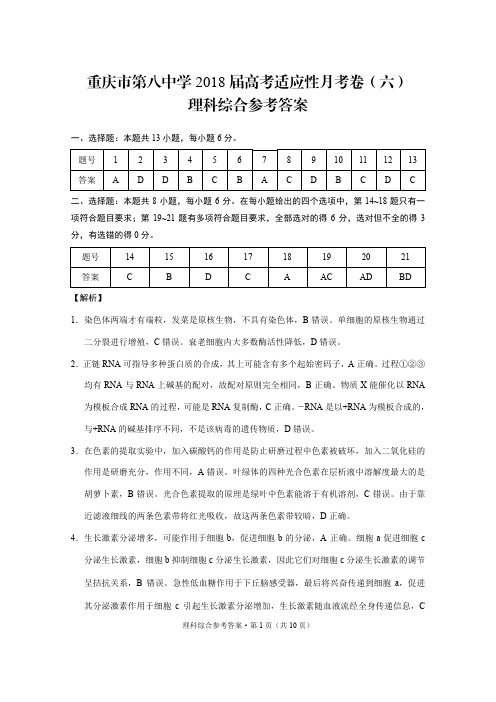

重庆市第八中学2018届高三适应性月考(八)数学试题(文)一、选择题1. 设集合,,则()A. B. C. D.2. 复数满足(为虚数单位),则()A. B. C. D.3. 如图是年至年我国三类专利申请总量的统计分析柱形图,则以下说法不.正确的是()A. 三类专利申请总量呈上升趋势B. 三类专利申请总量与年份呈正相关C. 年实用新型专利的数量与上一年相比有所增长D. 年发明专利的数量与上一年基本持平4. 若抛物线的准线恰好过双曲线的焦点,则()A. B. C. D.5. 如图,网格纸上小正方形的边长为,粗线画的是某几何体的三视图,则该几何体的体积为()A. B. C. D.6. 已知角的顶点与原点重合,始边与轴的正半轴重合,终边位于第三象限且过点,若,则()A. B. C. D.7. 在正方体中,点是线段上任意一点,则下列结论正确的是()A. B. C. D.8. 执行如图所示的程序框图,则输出的值为()A. B. C. D.9. 已知函数,若,则的取值为()A. B. C. 或 D. 或10. 已知函数的最小正周期为,且函数的一条对称轴为,则的最小值为()A. B. C. D.11. 公差与首项相等的等差数列的前项和为,且.记,其中表示不超过的最大整数,如,,则数列的前项和为()A. B. C. D.12. 已知,分别为椭圆:的左、右顶点,点,在上,直线垂直于轴且过的右焦点,直线与轴交于点,若,则椭圆的离心率为()A. B. C. D.二、填空题13. 曲线在点处的切线方程为__________.14. 已知各项为正数的等比数列的前项和为,,.若,则__________.15. 设,是不共线的两个非零向量,若,,,且点,,在同一直线上,则__________.16. 函数的图象与的图象关于直线对称,且相交于点,则__________.三、解答题17. 在中,角,,所对的边分别为,,,若,.(1)求和;(2)若,求的面积.18. 某种产品,每售出一吨可获利万元,每积压一吨则亏损万元.某经销商统计出过去年里市场年需求量的频数分布表如下表所示.(1)求过去年年需求量的平均值;(每个区间的年需求量用中间值代替)(2)今年该经销商欲进货吨,以(单位:吨,)表示今年的年需求量,以(单位:万元)表示今年销售的利润,试将表示的函数解析式,并求今年的年利润不少于万元的概率.19. 如图,在边长为的正方形中,点,分别为,的中点,将折到的位置.(1)求证:;(2)若,求五棱锥的体积.20. 已知点,圆:,点是圆上一动点,线段的垂直平分线与交于点.(1)求点的轨迹的方程;(2)曲线与轴交于点,,直线过点且垂直于轴,点在直线上,点在曲线上,若,试判断直线与曲线的交点的个数.21. 已知函数.(1)当时,讨论的导函数的单调性;(2)当时,,求的取值范围.请考生在22、23两题中任选一题作答.如果多做,则按所做的第一题记分.22. [选修4-4:坐标系与参数方程]已知在平面直角坐标系中,曲线的参数方程为(为参数,).在以为极点,轴的正半轴为极轴的极坐标系中,曲线:.(1)求曲线,的普通方程;(2)若直线的极坐标方程为,其中满足,若与在第一象限的公共点在上,求实数的值.23. [选修4-5:不等式选讲]已知关于的不等式.(1)当时,解关于的不等式;(2)若函数存在零点,求实数的取值范围.【参考答案】一、选择题1. 【答案】A【解析】分析:先化简集合A,再判断选项正误得解.详解:由题得,因为,所以,故答案为:A2.【答案】B【解析】分析:直接根据求复数z.详解:由题得故答案为:B3. 【答案】D【解析】分析:结合统计分析柱形图逐一判断得解.详解:由于从2004年到2013年的柱形图的高度逐年增加,所以三类专利申请总量呈上升趋势,所以选项A正确,三类专利申请总量与年份呈正相关,所以选项B正确.由于年实用新型专利的数量与2012年相比有所增长,所以选项C正确.由于年发明专利的数量与上一年要多,所以选项D错误.故答案为:D4. 【答案】C【解析】分析:根据题意得到关于p的方程,解方程即得p的值.详解:因为抛物线的准线为x=p, 双曲线的右焦点为,所以故答案为:C5. 【答案】C【解析】分析:先通过三视图找到几何体原图,再求组合体的体积.详解:由三视图得几何题是一个组合体,左边是半个球,球的半径为1,中间是一个底面半径为1的圆,高为2,最右边是一个底面半径为1的圆锥,高为2.所以组合体的体积为故答案为:C6. 【答案】B【解析】分析:先根据已知条件得到再根据计算出的值.详解:由题得因为,所以所以故答案为:B7. 【答案】C【解析】分析:先证明⊥平面ABM,再证明.详解:由题得⊥,⊥AB,因为AB,平面ABM,且AB∩=B,所以⊥平面ABM,所以.故答案为:C8. 【答案】D【解析】分析:按照程序框图模拟运行得解.详解:运行程序如下:m=1,n=1,1≤10,m=2,n=1,2≤10,m=3,n=2,3≤10,m=5,n=4,5≤10,m=9,n=8,9≤10,m=17,n=16,17>10,n=16.故答案为:D点睛:本题主要考查程序框图,意在考查学生对程序框图的理解和掌握水平.9. 【答案】D【解析】分析:先求出f(b)=0或2,再对b分两种情况讨论,分别得到b的值.详解:由题得f(0)=f(2)=1,所以f(b)=0或2,当b<1时,没有解;当b≥1时,故答案为:D10. 【答案】B【解析】分析:先根据函数的周期求出w的值,再根据对称轴求出a的值,再求函数的最小值.详解:由题得,所以f(x)=asin2x+cos2x,所以所以所以f(x)= sin2x+cos2x=2sin(2x+),所以的最小值为-2.故答案为:B11. 【答案】C【解析】分析:先求出数列的通项,再分组求数列的前项和.详解:由题得所以所以所以数列的前项和为.故答案为:C12. 【答案】A【解析】分析:先根据MO||PF得到,再根据得到,最后解方程即得解.详解:设椭圆的右焦点为F,由题得MO||PF,所以,因为,所以,所以所以.故答案为:A.二、填空题13.【答案】.【解析】分析:先求切点坐标,再求切线的斜率,最后求切线方程.详解:由题得f(1)=,所以切点为,由题得所以切线方程为y=.故答案为:14.【答案】6.【解析】分析:先根据,计算出,再根据求出n的值.详解:由题得因为,所以故答案为:615.【答案】.【解析】分析:先利用向量的减法法则求出,再根据点,,在同一直线上求k的值.详解:由题得因为点,,在同一直线上,所以故答案为:16.【答案】0.【解析】分析:先根据点(-1,1)在曲线的图象上求出m的值,再求函数f(x)的解析式,再求f(-e)的值.详解:因为点(-1,1)在曲线的图象上,所以所以故答案为:0三、解答题17. 解:(1)由,得,所以,又由.(2)由题知,,再由余弦定理得,解得,所以的面积.18. 解:(1)设年需求量的平均值为吨,则(吨).(2)由今年的需求量为吨,年获利为万元,当时,,当时,,故,由,,,所以求得今年的年利润不少于万元的概率为.19. (1)证明:如图,由题知,,,所以,所以.设的中点为,连接,,则,又由于,所以,又因为,所以平面,所以.(2)解:∵平面,平面,平面平面,所以平面平面,如图,过点作,则平面.在中,,,,所以,由,解得.又因为,所以五棱锥的体积为.20. 解:(1)连接,由题知,所以,即点的轨迹是以,为焦点的椭圆,因此,,所以,所以点的轨迹的方程为.(2)不妨设,,则直线:,设,则,所以,因此直线:.设,联立直线与椭圆的方程可得,因此,所以,所以,所以直线的方程为,即,其中,,联立直线:与椭圆,得,所以,所以与曲线只有一个交点.21. 解:(1)当时,,,当时,,的单调递减区间为;当时,,的单调递增区间为.(2),(i)当时,,所以在上单调递增,.(ii)当时,,由,得,①当时,,所以时,,在上单调递增,又由,所以,即在上单调递增,所以有.②当时,,当时,,在上单调递减,又由,所以,所以在上单调递减,所以有,故此时不满足,综上,.请考生在22、23两题中任选一题作答.如果多做,则按所做的第一题记分.22.解:(1):,:.(2)直线的普通方程为,由得与在第一象限的公共点的坐标为,代入曲线得.23.解:(1)当时,,当时,,∴;当时,,无解;当时,,∴,综上所述,不等式的解集为.(2)根据题意,存在零点等价于,当时,,∴;当时,,∴,当时,,∴,综上所述,,∴,,故实数的取值范围是.。

重庆市第八中学2018届高考适应性月考卷(八)文科数学一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 设集合,,则()A. B. C. D.【答案】A【解析】分析:先化简集合A,再判断选项正误得解.详解:由题得,因为,所以,故答案为:A点睛:本题主要考查集合的化简与交集并集运算,意在考查学生对这些基础知识的掌握水平.2. 复数满足(为虚数单位),则()A. B. C. D.【答案】B【解析】分析:直接根据求复数z.详解:由题得故答案为:B点睛:(1)本题主要考查复数的除法运算和复数的模,意在考查学生对这些基础知识的掌握水平和基本运算能力.(2)3. 如图是年至年我国三类专利申请总量的统计分析柱形图,则以下说法不.正确的是()A. 三类专利申请总量呈上升趋势B. 三类专利申请总量与年份呈正相关C. 年实用新型专利的数量与上一年相比有所增长D. 年发明专利的数量与上一年基本持平【答案】D【解析】分析:结合统计分析柱形图逐一判断得解.详解:由于从2004年到2013年的柱形图的高度逐年增加,所以三类专利申请总量呈上升趋势,所以选项A正确,三类专利申请总量与年份呈正相关,所以选项B正确.由于年实用新型专利的数量与2012年相比有所增长,所以选项C正确.由于年发明专利的数量与上一年要多,所以选项D错误.故答案为:D点睛:本题主要考查对柱形图的观察和理解,意在考查学生对这些基础知识的掌握水平和观察分析能力.4. 若抛物线的准线恰好过双曲线的焦点,则()A. B. C. D.【答案】C【解析】分析:根据题意得到关于p的方程,解方程即得p的值.详解:因为抛物线的准线为x=p, 双曲线的右焦点为,所以故答案为:C点睛:(1)本题主要考查抛物线和双曲线的几何性质,意在考查学生对这些基础知识的掌握水平和基本的计算能力.(2)研究圆锥曲线的问题,首先必须把圆锥曲线的方程化成标准方程,所以本题先要把双曲线的方程化为,再计算.5. 如图,网格纸上小正方形的边长为,粗线画的是某几何体的三视图,则该几何体的体积为()A. B. C. D.【答案】C【解析】分析:先通过三视图找到几何体原图,再求组合体的体积.详解:由三视图得几何题是一个组合体,左边是半个球,球的半径为1,中间是一个底面半径为1的圆,高为2,最右边是一个底面半径为1的圆锥,高为2.所以组合体的体积为故答案为:C点睛:(1)本题主要考查三视图和组合体的体积的计算,意在考查学生对这些基础知识的掌握水平和空间想象能力.(2)通过三视图找原图常用的有直接法和模型法,本题选择直接法比较简洁方便.6. 已知角的顶点与原点重合,始边与轴的正半轴重合,终边位于第三象限且过点,若,则()A. B. C. D.【答案】B【解析】分析:先根据已知条件得到再根据计算出的值.详解:由题得因为,所以所以故答案为:B点睛:(1)本题主要考查三角函数的坐标定义和三角求值,意在考查学生对这些基础知识的掌握水平和基本的运算能力.(2)点p(x,y)是角终边上的任意的一点(原点除外),r代表点到原点的距离,则sin= cos= tan=.7. 在正方体中,点是线段上任意一点,则下列结论正确的是()A. B. C. D.【答案】C【解析】分析:先证明⊥平面ABM,再证明.详解:由题得⊥,⊥AB,因为AB,平面ABM,且AB∩=B,所以⊥平面ABM,所以.故答案为:C点睛:(1)本题主要考查空间直线平面的位置关系的证明,意在考查学生对这些基础知识的掌握水平和空间想象转化能力.(2)证明空间直线平面的位置关系可以利用几何法和向量法,本题两种方法都可以.8. 执行如图所示的程序框图,则输出的值为()A. B. C. D.【答案】D【解析】分析:按照程序框图模拟运行得解.详解:运行程序如下:m=1,n=1,1≤10,m=2,n=1,2≤10,m=3,n=2,3≤10,m=5,n=4,5≤10,m=9,n=8,9≤10,m=17,n=16,17>10,n=16.故答案为:D点睛:本题主要考查程序框图,意在考查学生对程序框图的理解和掌握水平.9. 已知函数,若,则的取值为()A. B. C. 或 D. 或【答案】D【解析】分析:先求出f(b)=0或2,再对b分两种情况讨论,分别得到b的值.详解:由题得f(0)=f(2)=1,所以f(b)=0或2,当b<1时,没有解;当b≥1时,故答案为:D点睛:(1)本题主要考查分段函数的计算,意在考查学生对分段函数的理解和掌握水平.(2)分段函数求值,先要看自变量在哪一段,再代入求值,如果不能确定就要分类讨论.10. 已知函数的最小正周期为,且函数的一条对称轴为,则的最小值为()A. B. C. D.【答案】B【解析】分析:先根据函数的周期求出w的值,再根据对称轴求出a的值,再求函数的最小值.详解:由题得,所以f(x)=asin2x+cos2x,所以所以所以f(x)= sin2x+cos2x=2sin(2x+),所以的最小值为-2.故答案为:B点睛:(1)本题主要考查三角函数的图像和性质,意在考查学生对这些基础知识的掌握水平和图像分析推理能力. (2)本题求a时,利用了,比较简洁,注意导数知识的灵活运用.11. 公差与首项相等的等差数列的前项和为,且.记,其中表示不超过的最大整数,如,,则数列的前项和为()A. B. C. D.【答案】C【解析】分析:先求出数列的通项,再分组求数列的前项和.详解:由题得所以所以所以数列的前项和为.故答案为:C点睛:(1)本题主要考查等差数列的通项和前n项和,考查学生接受新定义及利用新定义解题的能力.(2)由于新数列的通项不方便求出,所以利用列举法比较恰当.12. 已知,分别为椭圆:的左、右顶点,点,在上,直线垂直于轴且过的右焦点,直线与轴交于点,若,则椭圆的离心率为()A. B. C. D.【答案】A【解析】分析:先根据MO||PF得到,再根据得到,最后解方程即得解.详解:设椭圆的右焦点为F,由题得MO||PF,所以,因为,所以,所以所以.故答案为:A点睛:(1)本题主要考查椭圆的几何性质和解三角形,意在考查学生对这些知识的掌握水平和分析推理的能力.(2) 求离心率一般有两种方法,方法一是直接法,直接根据已知求出a和c的值,再求离心率.方法二是解方程法,根据已知得到关于离心率e的方程,再解方程.本题利用的是方法二,比较简洁.二、填空题(本大题共4小题,每小题5分,共20分)13. 曲线在点处的切线方程为__________.【答案】.【解析】分析:先求切点坐标,再求切线的斜率,最后求切线方程.详解:由题得f(1)=,所以切点为,由题得所以切线方程为y=.故答案为:点睛:(1)本题主要考查导数的几何意义和求切线方程,意在考查学生对这些基础知识的掌握水平.(2)遇到切线的问题,一般先找切点,再求切线的斜率,再求切线的方程.14. 已知各项为正数的等比数列的前项和为,,.若,则__________.【答案】6.【解析】分析:先根据,计算出,再根据求出n的值.详解:由题得因为,所以故答案为:6点睛:(1)本题主要考查等比数列的通项和求和,意在考查学生对这些基础知识的掌握水平和基本的计算能力.(2)等比数列的前n项和,要分类讨论,如果n比较小,可以不用这个公式,直接用定义比较简洁,如15. 设,是不共线的两个非零向量,若,,,且点,,在同一直线上,则__________.【答案】.【解析】分析:先利用向量的减法法则求出,再根据点,,在同一直线上求k的值.详解:由题得因为点,,在同一直线上,所以故答案为:点睛:(1)本题主要考查向量的运算和共线向量的性质,意在考查学生对这些基础知识的掌握水平.(2)三点共线.16. 函数的图象与的图象关于直线对称,且相交于点,则__________.【答案】0.【解析】分析:先根据点(-1,1)在曲线的图象上求出m的值,再求函数f(x)的解析式,再求f(-e)的值.详解:因为点(-1,1)在曲线的图象上,所以所以故答案为:0点睛:(1)本题主要考查函数的对称性和函数求值,意在考查学生对这些基础知识的掌握水平和分析推理能力.(2)解答本题的关键是求f(x)的解析式.三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)17. 在中,角,,所对的边分别为,,,若,.(1)求和;(2)若,求的面积.【答案】(1);.(2).【解析】分析:(1)先化简求出A的值,再根据7c=5a求sinC的值.(2)先利用余弦定理求b的值,再求的面积.........................详解:(1)由,得,所以,又由.(2)由题知,,再由余弦定理得,解得,所以的面积.点睛:本题主要考查正弦定理余弦定理解三角形,考查三角形面积的求法,属于基础题.18. 某种产品,每售出一吨可获利万元,每积压一吨则亏损万元.某经销商统计出过去年里市场年需求量的频数分布表如下表所示.(1)求过去年年需求量的平均值;(每个区间的年需求量用中间值代替)(2)今年该经销商欲进货吨,以(单位:吨,)表示今年的年需求量,以(单位:万元)表示今年销售的利润,试将表示的函数解析式,并求今年的年利润不少于万元的概率.【答案】(1)86.5(吨).(2);.【解析】分析:(1)直接利用平均数的公式求过去年年需求量的平均值.(2)先对x 分类讨论,将表示的函数解析式,再求今年的年利润不少于万元的概率.详解:(1)设年需求量的平均值为吨,则(吨).(2)由今年的需求量为吨,年获利为万元,当时,,当时,,故, 由,,,所以求得今年的年利润不少于万元的概率为.点睛:(1)本题主要考查平均数的计算和概率的计算,考查函数解析式的求法,意在考查学生对这些基础知识的掌握水平和分析推理能力.(2)求平均数一般利用平均数的公式计算.19. 如图,在边长为的正方形中,点,分别为,的中点,将折到的位置.(1)求证:;(2)若,求五棱锥的体积.【答案】(1)证明见解析.(2).【解析】分析:(1)先证明平面,再证明.(2)先求五棱锥的高PH,再利用公式求五棱锥的体积详解:(1)证明:如图,由题知,,,所以,所以.设的中点为,连接,,则,又由于,所以,又因为,所以平面,所以.(2)解:∵平面,平面,平面平面,所以平面平面,如图,过点作,则平面.在中,,,,所以,由,解得.又因为,所以五棱锥的体积为.点睛:(1)本题主要考查空间直线平面位置关系的证明和几何体体积的计算,意在考查学生对这些基础知识的掌握水平和空间想象转化能力.(2)求几何体的体积常用的有割补法、公式法和转化法.20. 已知点,圆:,点是圆上一动点,线段的垂直平分线与交于点.(1)求点的轨迹的方程;(2)曲线与轴交于点,,直线过点且垂直于轴,点在直线上,点在曲线上,若,试判断直线与曲线的交点的个数.【答案】(1).(2)与曲线只有一个交点.【解析】分析: (1)利用待定系数法求点P 的轨迹E 的方程.(2)先求直线的方程为,再联立椭圆,求得△=0得与曲线只有一个交点.详解:(1)连接,由题知,所以,即点的轨迹是以,为焦点的椭圆,因此,,所以,所以点的轨迹的方程为.(2)不妨设,,则直线:,设,则,所以,因此直线:.设,联立直线与椭圆的方程可得,因此,所以,所以,所以直线的方程为,即,其中,,联立直线:与椭圆,得,所以,所以与曲线只有一个交点.点睛:(1)本题主要考查轨迹方程的求法,考查直线和椭圆的位置关系,意在考查学生对这些知识的掌握水平和分析推理计算能力.(2)本题的关键是联立直线和椭圆的方程的化简,如果直接把和椭圆联立,则计算量比较大,本题换元,,计算量减少了许多.21. 已知函数.(1)当时,讨论的导函数的单调性;(2)当时,,求的取值范围.【答案】(1) 当时,,的单调递减区间为;当时,,的单调递增区间为.(2).【解析】分析:(1)先求导得,再求导得,再求函数的单调性.(2)对a分类讨论求函数f(x)的最小值得a的取值范围.详解:(1)当时,,,当时,,的单调递减区间为;当时,,的单调递增区间为.(2),(i)当时,,所以在上单调递增,.(ii)当时,,由,得,①当时,,所以时,,在上单调递增,又由,所以,即在上单调递增,所以有.②当时,,当时,,在上单调递减,又由,所以,所以在上单调递减,所以有,故此时不满足,综上,.点睛:(1)本题主要考查利用导数求函数的单调性、最值,考查利用导数研究恒成立问题,意在考查学生对这些基础知识的掌握水平和分析推理能力.(2)本题的关键是第2问,求导之后,还需要二次求导,才能找到函数的单调性.一次求导之后,如果不易解答,可以二次求导.请考生在22、23两题中任选一题作答,并用2B铅笔在答题卡上把所选题目的题号涂黑.注意所做题目的题号必须与所涂题目的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题记分.22. [选修4-4:坐标系与参数方程]已知在平面直角坐标系中,曲线的参数方程为(为参数,).在以为极点,轴的正半轴为极轴的极坐标系中,曲线:.(1)求曲线,的普通方程;(2)若直线的极坐标方程为,其中满足,若与在第一象限的公共点在上,求实数的值.【答案】(1):;:.(2).【解析】分析:(1)消参得到的普通方程,把极坐标的公式代入曲线的方程得到的普通方程.(2)先求与在第一象限的公共点,再代入曲线方程得a的值.详解:(1):,:.(2)直线的普通方程为,由得与在第一象限的公共点的坐标为,代入曲线得.点睛:本题主要考查参数方程极坐标方程与普通方程的互化,考查直线与曲线的位置关系,意在考查学生对这些知识的掌握水平和基本的计算能力.23. [选修4-5:不等式选讲]已知关于的不等式.(1)当时,解关于的不等式;(2)若函数存在零点,求实数的取值范围.【答案】(1).(2).【解析】分析:(1)利用零点分类讨论法解不等式.(2)先转化为,再分类讨论求的值和解不等式得的取值范围.详解:(1)当时,,当时,,∴;当时,,无解;当时,,∴,综上所述,不等式的解集为.(2)根据题意,存在零点等价于,当时,,∴;当时,,∴,当时,,∴,综上所述,,∴,,故实数的取值范围是.点睛:(1)本题主要考查绝对值不等式的解法,考查存在性问题,意在考查学生对这些知识的掌握水平和基本的计算能力.(2)解答第2问的关键是转化成和求,注意这里是存在性问题,不是求.。