2012高考数学核心考点复习：第6课时 不等式的应用

2012届高考数学知识不等式复习讲义高中数学复习讲义第六章不等式【知识图解】【方法点拨】不等式是高中数学的重要内容之一，不等式的性质是解、证不等式的基础，两个正数的算术平均数不小于它们的几何平均数的定理及其变形在不等式的证明和解决有关不等式的实际问题中发挥着重要的作用.解不等式是研究方程和函数的重要工具，不等式的概念和性质涉及到求最大（小）值，比较大小，求参数的取值范围等，不等式的解法包括解不等式和求参数，不等式的综合题主要是不等式与集合、函数、数列、三角函数、解析几何、导数等知识的综合，综合性强，难度较大，是高考命题的热点，也是高考复习的难点，1. 掌握用基本不等式求解最值问题，能用基本不等式证明简单的不等式，利用基本不等式求最值时一定要紧扣“一正、二定、三相等”这三个条件。

2. 一元二次不等式是一类重要的不等式，要掌握一元二次不等式的解法，了解一元二次不等式与相应函数、方程的联系和相互转化。

3. 线性规划问题有着丰富的实际背景，且作为最优化方法之一又与人们日常生活密切相关，对于这部分内容应能用平面区域表示二元一次不等式组，能解决简单的线性规划问题。

同时注意数形结合的思想在线性规划中的运用。

第1课基本不等式【考点导读】1. 能用基本不等式证明其他的不等式，能用基本不等式求解简单的最值问题。

2. 能用基本不等式解决综合形较强的问题。

【基础练习】1. “ a>b>0 ”是“ ab2.的最小值为3. 已知，且，则的最大值为4. 已知，则的最小值是2【范例导析】例1.已知，求函数的最大值.分析：由于，所以首先要调整符号.解：••••••••• y=4x-2+= < -2+3=1当且仅当，即x=1时，上式成立，故当x=1时，.例2. (1)已知a, b为正常数，x、y为正实数，且，求x+y的最小值。

(2)已知，且，求的最大值.分析：问题(1)可以采用常数代换的方法也可以进行变量代换从而转化为一元函数再利用基本不等式求解；问题(2)既可以直接利用基本不等式将题目中的等式转化为关于的不等式，也可以采用变量代换转换为一元函数再求解解:(1)法一：直接利用基本不等式：》当且仅当，即时等号成立法二：由得••• x>0, y>0 , a>0「.由>0 得y-b>0 二x+y >当且仅当，即时，等号成立(2)法一：由，可得，.注意到.可得，.当且仅当，即时等号成立，代入中得，故的最大值为法二：,代入中得：解此不等式得.下面解法见解法一，下略.点拨：求条件最值的问题，基本思想是借助条件化二元函数为一元函数，代入法是最基本的方法，也可考虑通过变形直接利用基本不等式解决.【反馈练习】1. 设a> 1,且,则的大小关系为> p>n2. 已知下列四个结论：①若则；②若，则；③若则；④若则。

高考数学不等式知识点归纳导读：我根据大家的需要整理了一份关于《高考数学不等式知识点归纳》的内容，具体内容：高考数学有些重点需要复习，其中包括不等式的内容。

下面我给大家带来高考数学不等式知识点，希望对你有帮助。

高考数学不等式知识点不等式概念用不等号可以将两个解析式连接...高考数学有些重点需要复习，其中包括不等式的内容。

下面我给大家带来高考数学不等式知识点，希望对你有帮助。

高考数学不等式知识点不等式概念用不等号可以将两个解析式连接起来所成的式子。

在一个式子中的数的关系,不全是等号,含不等符号的式子，那它就是一个不等式.例如x+yxy，-2x1，x>0 ，xx是超越不等式。

不等式性质①如果x>y，那么yy;(对称性)②如果x>y，y>z;那么x>z;(传递性)③如果x>y，而z为任意实数或整式，那么x+z>y+z;(加法原则，或叫同向不等式可加性)④ 如果x>y，z>0，那么xz>yz;如果x>y，z<0，那么xz⑤如果x>y，z>0，那么x÷z>y÷z;如果x>y，z<0，那么x÷z<y÷z;⑥如果x>y，m>n，那么x+m>y+n;(充分不必要条件)⑦如果x>y>0，m>n>0，那么xm>yn;⑧如果x>y>0，那么x的n次幂>y的n次幂(n为正数或负数) [1]或者说，不等式的基本性质有：①对称性;②传递性：③加法单调性：即同向不等式可加性：④乘法单调性：⑤同向正值不等式可乘性：;⑥正值不等式可乘方：⑦正值不等式可开方：：⑧倒数法则。

[2]......如果由不等式的基本性质出发，通过逻辑推理，可以论证大量的初等不等式，以上是其中比较有名的。

不等式原理编辑主要的有：①不等式F(x)F(x)同解。

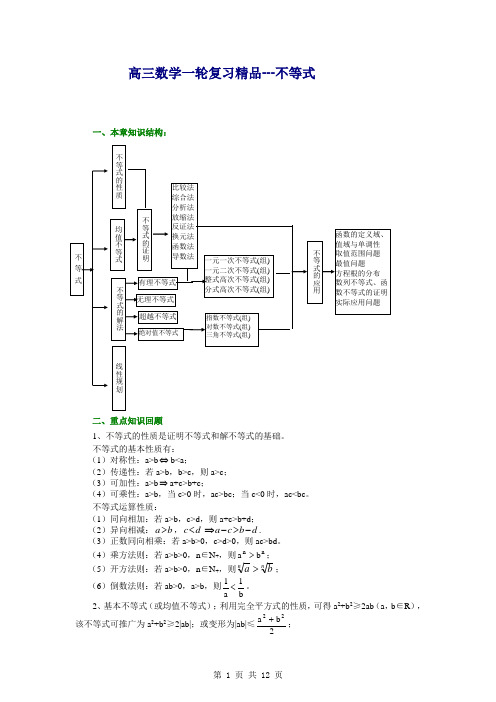
高三数学一轮复习精品---不等式一、本章知识结构：二、重点知识回顾1、不等式的性质是证明不等式和解不等式的基础。

不等式的基本性质有： （1）对称性：a>b ⇔b<a ；（2）传递性：若a>b ，b>c ，则a>c ； （3）可加性：a>b ⇒a+c>b+c ；（4）可乘性：a>b ，当c>0时，ac>bc ；当c<0时，ac<bc 。

不等式运算性质：（1）同向相加：若a>b ，c>d ，则a+c>b+d ； （2）异向相减：b a >，d c <d b c a ->-⇒.（3）正数同向相乘：若a>b>0，c>d>0，则ac>bd 。

（4）乘方法则：若a>b>0，n ∈N +，则n n b a >；（5）开方法则：若a>b>0，n ∈N +，则n n b a >；（6）倒数法则：若ab>0，a>b ，则b1a 1<。

2、基本不等式（或均值不等式）；利用完全平方式的性质，可得a 2+b 2≥2ab （a ，b ∈R ），该不等式可推广为a 2+b 2≥2|ab|；或变形为|ab|≤2b a 22+；无理不等式 不 等 式不等式的性质均值不等式不等式的解法比较法 综合法 分析法 放缩法 反证法 换元法 函数法 导数法不等式的证明有理不等式超越不等式绝对值不等式一元一次不等式(组) 一元二次不等式(组) 整式高次不等式(组) 分式高次不等式(组)指数不等式(组) 对数不等式(组) 三角不等式(组)不等式的应用函数的定义域、 值域与单调性 取值范围问题 最值问题 方程根的分布 数列不等式、函 数不等式的证明 实际应用问题线性规划当a ，b ≥0时，a+b ≥ab 2或ab ≤22b a ⎪⎭⎫⎝⎛+.3、不等式的证明：（1）不等式证明的常用方法：比较法，公式法，分析法，反证法，换元法，放缩法； （2）在不等式证明过程中，应注重与不等式的运算性质联合使用； （3）证明不等式的过程中，放大或缩小应适度。

不等式 知识点总结精华考试内容：不等式．不等式的基本性质．不等式的证明．不等式的解法．含绝对值的不等式． 考试要求：（1）理解不等式的性质及其证明．（2）掌握两个（不扩展到三个）正数的算术平均数不小于它们的几何平均数的定理，并会简单的应用．（3）掌握分析法、综合法、比较法证明简单的不等式． （4）掌握简单不等式的解法．（5）理解不等式│a │-│b │≤│a+b │≤│a │+│b │不 等 式 知识要点三.不等式、线性规划、算法1.掌握课本上的几个不等式性质，注意使用条件，另外需要特别注意： ①若0ab >,b a >,则11ab>.即不等式两边同号时,不等式两边取倒数,不等号方向要改变.②如果对不等式两边同时乘以一个代数式,要注意它的正负号,如果正负号未定,要注意分类讨论.③取倒数:0a b <<⇔011ab>>；0a b >>⇔011ab<<；如112x-<<，等价于110x-<<或102x <<2.掌握几类不等式(一元一次、二次、绝对值不等式、简单的指数、对数不等式)的解法,尤其注意用分类讨论的思想解含参数的不等式；勿忘数轴标根法,零点分区间法.3.掌握重要不等式,(1)均值不等式：若0,>b a ,2211a b a b++≥(当且仅当b a =时取等号)使用条件：“一正二定三相等 ”， 常用的方法为：拆、凑、平方等； (2),,a b c R ∈，222a b c ab bc ca ++≥++(当且仅当a b c ==时,取等号)； (3)公式注意变形如：22222()ab a b ++≥,22()a b ab +≤；若0,0a b m >>>,则b b m aa m++<(真分数的性质)；4.证明不等式常用方法：⑴比较法：作差比较：0A B A B -≤⇔≤.注意：若两个正数作差比较有困难,可以通过它们的平方差来比较大小；⑵综合法：由因导果；⑶分析法：执果索因.基本步骤：要证…需证…,只需证…； ⑷反证法：正难则反；⑸放缩法：将不等式一侧适当的放大或缩小以达证题目的.放缩法的方法有：①添加或舍去一些项,||a >n >.②将分子或分母放大(或缩小)③利用基本不等式,如：(1)2n n ++<.④利用常用结论：0111-=<；2211111111(1)(1)1kk k kkk kk k++---=<<=-(程度大)；0322111111211()kkk k --+<=-(程度小)；⑹换元法：减少不等式中变量,以使问题化难为易,化繁为简,常用的换元有三角换元、代数换元.如：知222x y a +=,可设cos ,sin x a y a θθ==；22221xy ab+=,可设cos ,sin x a y b θθ==；6.（1）一元二次不等式ax bx c a 200++>≠()或ax bx c a 200++<≠⇒()分a >0及a <0情况分别解之，如设0a >,12,x x 是方程20ax bx c ++=的两实根，且12x x <，则其解集如下表：如解关于x 的不等式：01)1(2<++-x a ax 。

高中数学第六章-不等式考试内容：不等式．不等式的基本性质．不等式的证明．不等式的解法．含绝对值的不等式． 考试要求：（1）理解不等式的性质及其证明．（2）掌握两个（不扩展到三个）正数的算术平均数不小于它们的几何平均数的定理，并会简单的应用． （3）掌握分析法、综合法、比较法证明简单的不等式．（4）掌握简单不等式的解法．（5）理解不等式│a │-│b │≤│a+b │≤│a │+│b │§06. 不 等 式 知识要点1. 不等式的基本概念（1） 不等（等）号的定义：.0;0;0b a b a b a b a b a b a <⇔<-=⇔=->⇔>-（2） 不等式的分类：绝对不等式；条件不等式；矛盾不等式.（3） 同向不等式与异向不等式.（4） 同解不等式与不等式的同解变形.2.不等式的基本性质（1）a b b a <⇔>（对称性）（2）c a c b b a >⇒>>,（传递性）（3）c b c a b a +>+⇒>（加法单调性）（4）d b c a d c b a +>+⇒>>,（同向不等式相加）（5）d b c a d c b a ->-⇒<>,（异向不等式相减）（6）bc ac c b a >⇒>>0,.（7）bc ac c b a <⇒<>0,（乘法单调性）（8）bd ac d c b a >⇒>>>>0,0（同向不等式相乘）(9)0,0a b a b c d c d>><<⇒>（异向不等式相除） 11(10),0a b ab a b>>⇒<（倒数关系） （11）)1,(0>∈>⇒>>n Z n b a b a n n 且（平方法则）（12）)1,(0>∈>⇒>>n Z n b a b a n n 且（开方法则）3.几个重要不等式（1）0,0||,2≥≥∈a a R a 则若（2）)2||2(2,2222ab ab b a ab b a R b a ≥≥+≥+∈+或则、若（当仅当a=b 时取等号）（3）如果a ,b 都是正数，那么.2a b +（当仅当a=b 时取等号） 极值定理：若,,,,x y R x y S xy P +∈+==则：○1如果P 是定值, 那么当x=y 时，S 的值最小； ○2如果S 是定值, 那么当x =y 时，P 的值最大. 利用极值定理求最值的必要条件： 一正、二定、三相等.,3a b c a b c R +++∈≥(4)若、、则（当仅当a=b=c 时取等号）0,2b a ab a b>+≥(5)若则（当仅当a=b 时取等号）2222(6)0||;||a x a x a x a x a x a x a a x a >>⇔>⇔<-><⇔<⇔-<<时，或（7）||||||||||||,b a b a b a R b a +≤±≤-∈则、若 4.几个著名不等式（1）平均不等式： 如果a ,b 都是正数，那么2112a b a b +≤+（当仅当a=b 时取等号）即：平方平均≥算术平均≥几何平均≥调和平均（a 、b 为正数）： 特别地，222()22a b a b ab ++≤≤（当a = b 时，222()22a b a b ab ++==） ),,,(332222时取等c b a R c b a c b a c b a ==∈⎪⎭⎫ ⎝⎛+++≥++⇒幂平均不等式：22122221)...(1...n n a a a na a a +++≥+++ 注：例如：22222()()()ac bd a b c d +≤++. 常用不等式的放缩法：①21111111(2)1(1)(1)1n n n n n n n nn n -==-≥++--1)2n n n n -==≥+-（2）柯西不等式： 时取等号当且仅当（则若n n n n n n n n b a b a b a b a b b b b a a a a b a b a b a b a R b b b b R a a a a ====+++++++≤++++∈∈ 332211223222122322212332211321321))(();,,,,,,,,（3）琴生不等式（特例）与凸函数、凹函数若定义在某区间上的函数f(x),对于定义域中任意两点1212,(),x x x x ≠有 12121212()()()()()().2222x x f x f x x x f x f x f f ++++≤≥或 则称f(x)为凸（或凹）函数.5.不等式证明的几种常用方法比较法、综合法、分析法、换元法、反证法、放缩法、构造法. 6.不等式的解法（1）整式不等式的解法（根轴法）.步骤：正化，求根，标轴，穿线（偶重根打结），定解.特例① 一元一次不等式ax >b 解的讨论；②一元二次不等式ax 2+bx +c >0(a ≠0)解的讨论.（2）分式不等式的解法：先移项通分标准化，则()()0()()0()()0;0()0()()f x g x f x f x f x g x g x g x g x ≥⎧>⇔>≥⇔⎨≠⎩ （3）无理不等式：转化为有理不等式求解1()0()0()()f x g x f x g x ⎧≥⎫⇒⎪⎬>⇔≥⎨⎭⎪>⎩定义域 ○2⎩⎨⎧<≥⎪⎩⎪⎨⎧>≥≥⇔>0)(0)()]([)(0)(0)()()(2x g x f x g x f x g x f x g x f 或 ○3⎪⎩⎪⎨⎧<≥≥⇔<2)]([)(0)(0)()()(x g x f x g x f x g x f （4）.指数不等式：转化为代数不等式()()()()()(1)()();(01)()()(0,0)()lg lg f x g x f x g x f x a a a f x g x a a a f x g x a b a b f x a b>>⇔>><<⇔<>>>⇔⋅> （5）对数不等式：转化为代数不等式()0()0log ()log ()(1)()0;log ()log ()(01)()0()()()()a a a a f x f x f x g x a g x f x g x a g x f x g x f x g x >>⎧⎧⎪⎪>>⇔>><<⇔>⎨⎨⎪⎪><⎩⎩（6）含绝对值不等式○1应用分类讨论思想去绝对值； ○2应用数形思想； ○3应用化归思想等价转化 ⎩⎨⎧>-<>≤⇔>⎩⎨⎧<<->⇔<)()()()(0)()0)(),((0)()(|)(|)()()(0)()(|)(|x g x f x g x f x g x g x f x g x g x f x g x f x g x g x g x f 或或不同时为注：常用不等式的解法举例（x 为正数）：①231124(1)2(1)(1)()22327x x x x x -=⋅--≤=②2222232(1)(1)124(1)()22327x x x y x x y y --=-⇒=≤=⇒≤类似于22sin cos sin (1sin )y x x x x ==-，③111||||||()2x x x x x x+=+≥与同号，故取等。

不等式的应用第一节：利用重要不等式证明不等式 1：知识要点（1）均值不等式：设12,,...,n a a a 是n 个正实数，记12111n nn H a a a =++⋅⋅⋅+n G =12nn a a a A n ++⋅⋅⋅=n Q =它们分别称为n 个正数的调和平均数，几何平均数，算术平均数，平方平均数。

有如下关系：n n n n H G A Q ≤≤≤.等号成立的充要条件是12n a a a ==⋅⋅⋅=。

（2）柯西（Cauchy ）不等式：设12,,n a a a ⋅⋅⋅和12,n b b b ⋅⋅⋅是给定的实数，则222222211221212()()()n n n n a b a b a b a a a b b b ++⋅⋅⋅+≤++⋅⋅⋅+++⋅⋅⋅+。

等号成立的充要条件是：存在,λμ（不全为零），使i i a b λμ= i=1,2,···n （3）柯西不等式的几个推论 ①若,,1,2,,i i a b R i n ∈=，则22111n i ni i n i iii a a b b ===⎛⎫⎪⎝⎭≥∑∑∑，当且仅当,1,2,,i i b a i n λ==时取等号。

特别地，()3212321323222121y y y x x x y x y x y x ++++≥++ ②2111n i ni i n i ii ii a a b a b ===⎛⎫⎪⎝⎭≥∑∑∑，当且仅当12n b b b ===时等号成立③若,1,2,3,,i a R i n +∈=，则2211nn i i i i n a a ==⎛⎫≥ ⎪⎝⎭∑∑，当且仅当12n a a a ===时等号成立④若,1,2,3,,i a R i n +∈=，则2111n n i i i i a n a ==⎛⎫⎛⎫≥ ⎪ ⎪⎝⎭⎝⎭∑∑，当且仅当12n a a a ===时（4）排序不等式设n n n j j j b b b a a a ,,,,,212121⋯≤⋯≤≤≤⋯≤≤是n ,,2,1⋯的一个排列，令1212012111122,,n j j n j n n n n n S a b a b a b S a b a b a b S a b a b a b -'=+++=++⋯+=++⋯+.则0.S S S '≤≤ 证明若1,1k n j j b >=，由111111111k k n n j k j k k j n j n j S a b a b a b a b a b a b -+--+-=+⋯++++⋯++. 设1111111111k n k n j k j k j k j n j n S a b a b a b a b a b a b -+--+-=+⋯++++⋯++， 则111n n k n j k j n S S a b a b a b a b -=+--()().01≥--=n k j a a b b n可见按上述方法调整后，S 的值不增，若此时在1S 中12n j -≠，仿上又可得2,S ，最多经过2n -步调整以后，若在2n S -中22j ≠，将其中的21j =与12j =互换，得到10n S S -=，则12n n S S --≥，故1210.n S S S S S -≥≥≥⋯≥=所以，.0S S ≤由于12n b b b -≥-≥⋯≥-，利用上面所证结论，得.S S S S ''-≤-⇒≥ 综上，不等式获证。