浅谈高考中三视图的学习

对高考三视图试题的分析与思考三视图是新课程中增加的内容之一，对于这部分内容，与立体几何中有关的证明计算问题交汇在一起进行考查已成为高考命题的新热点。

高考中对空间几何体的三视图的考查，主要有三个层次的要求：能画、能识别和能运用。

因此，首先要熟练掌握三视图的概念和画图要求，其次要熟悉柱、锥、台、球各种基本几何体和它们组成的简单组合体，第三要熟练各种几何体的表面积、体积的计算公式和方法，最后要熟悉如下三种基本题型。

一、以几何体为载体，考查三视图的画法《课标》指出：能画出简单空间图形的三视图.即要求学生在给出简单几何体的条件下，能够根据几何体的正视图、侧视图、俯视图的定义，画出其三视图。

画图时学生应注意三视图的特点“主左一样高, 主俯一样长，俯左一样宽”。

例1（2011 全国卷）在一个几何体的三视图中,正视图和俯视图如图所示，则相应的侧视图可以为（）解析：由几何体的正视图和俯视图可知，该几何体的底面为半圆和等腰三角形，其侧视图可以是一个由等腰三角形及底边上的高构成的平面图形，故选D。

点评：本题是考查三视图的作法，属于三视图的基本题型，但由几何体的正视图、俯视图要求学生确定侧视图，构思独特，能考查学生的基本功及逻辑思维能力、推理能力和空间想象能力。

二、给出三视图，考查几何体的体积、表面积等高考以三视图还原几何体为载体，结合面积和体积的计算进行命题。

2011 年天津、安徽、北京、湖南等多个省市都以此题型命题。

例2（2011 湖南卷）右图是某几何体的三视图，则该几何体的体积为（）解析：本题是球和长方体的组合体，故体积V=32×2+43π（32）3=18+92π。

点评：以球和长方体的组合体为背景，以三视图基础知识为依托，考查学生运用三视图的基本知识以及空间想象、逻辑思维的能力和计算能力。

如果将俯视图的外接正方形去掉，那么几何体变成由球和圆柱组合而成，就变成了另一道题。

三、给出三视图考查原几何体中有关元素的平行垂直关系以三视图为载体，考查还原几何体中平行垂直的证明及空间角、空间距离的计算，体现三视图在立体几何中的基础性，充分发挥三视图的载体功能，将立体几何的重要知识点有机地结合在一起。

探究高中数学中的三视图与投影在高中数学课程中，三视图与投影是一个重要的概念。

它们被广泛应用于工程、建筑和设计等领域，帮助我们更好地理解和表达三维物体。

本文将探究三视图与投影的概念、应用和相关原理。

一、三视图的概念与应用三视图是指通过不同的视角观察一个三维物体，得到的三个二维图形。

通常，我们将三视图分为俯视图、正视图和侧视图。

俯视图是从物体的上方向下观察，正视图是从物体的正面观察，侧视图是从物体的侧面观察。

三视图在工程和设计中起着重要的作用。

它们可以帮助工程师和设计师更好地理解和表达物体的形状、尺寸和结构。

通过三视图，我们可以清晰地看到物体的各个面，从而更好地进行设计和制造。

二、投影的概念与原理投影是指将三维物体的形状和结构投射到一个平面上，得到的二维图形。

在数学中，我们常用的投影有平行投影和透视投影。

平行投影是指将物体的各个点沿着平行线投射到平面上。

在平行投影中，物体的形状和尺寸保持不变，只是投影到平面上的位置发生变化。

透视投影是指将物体的各个点沿着射线投射到平面上。

在透视投影中，物体的形状和尺寸会发生变化，远离观察者的部分会显得较小。

投影的原理基于几何学中的相似三角形原理。

通过相似三角形的比例关系，我们可以计算出投影和实物之间的关系，从而得到物体在平面上的投影图形。

三、三视图与投影的关系三视图和投影之间存在密切的关系。

三视图是通过不同的视角观察物体得到的二维图形，而投影则是将物体投射到平面上得到的二维图形。

三视图可以看作是物体在不同视角下的投影。

通过三视图和投影，我们可以更全面地了解一个物体的形状和结构。

三视图提供了物体的各个面的信息，而投影则提供了物体在平面上的尺寸和位置信息。

通过综合三视图和投影，我们可以还原出物体的三维形状。

四、实际应用举例三视图和投影在实际应用中有广泛的应用。

以建筑设计为例，设计师通常会绘制物体的三视图和投影图来进行设计和制造。

通过三视图和投影，设计师可以更好地理解建筑物的结构和尺寸，从而进行精确的设计和施工。

高中数学中的三视知识点总结三视是指从不同角度观察一个物体时所得到的图形，包括主视图、左视图和顶视图。

在高中数学中，三视是一个重要的概念，涉及到几何图形的理解和建模。

以下是高中数学中的三视知识点的总结。

1. 主视图：主视图是指一个物体从正面朝向观察者时所得到的图形。

在主视图中，我们可以观察到物体的宽度、高度和部分深度。

主视图通常用正方向的箭头表示，箭头指向主视图的方向。

2. 左视图：左视图是指一个物体从左侧朝向观察者时所得到的图形。

左视图通常与主视图相互垂直，能够展示物体的厚度和深度。

左视图也可以用箭头表示，箭头指向左视图的方向。

3. 顶视图：顶视图是指一个物体从上方朝向观察者时所得到的图形。

顶视图可以展示物体的长度和宽度，但没有深度信息。

顶视图也可以用箭头表示，箭头指向顶视图的方向。

三视图常常出现在几何图形的建模中。

通过观察三视图，我们可以更准确地理解和描述一个物体的形状和尺寸。

在数学中，我们通过三视图来解决以下几个问题：1. 三视图的绘制：为了绘制一个物体的三视图，我们首先需要了解物体的尺寸和形状。

我们可以通过已知的信息，比如物体的长度、宽度和高度，来绘制主视图、左视图和顶视图。

绘制三视图需要一定的几何知识和技巧。

2. 三视图的旋转：通过旋转物体，我们可以观察到不同的视图。

在数学中，我们可以通过旋转主视图、左视图和顶视图，来得到其他角度的视图。

通过观察这些视图，我们可以更全面地认识一个物体。

3. 三视图的投影：在三维空间中，一个物体在某个平面上的投影就是其相应视图。

通过投影，我们可以将三维物体转化为二维图形。

在几何学中，投影是一个重要的概念，可以帮助我们研究空间中的物体。

除了上述的知识点，三视图还与其他数学概念有一定的联系。

比如，在解方程和计算几何中，我们可以通过三视图来解决问题。

三视图还与空间几何和立体几何等知识有关联。

总结：在高中数学中，三视是一个重要的概念，涉及到几何图形的建模和分析。

通过观察和分析三视图，我们可以更准确地描述和理解一个物体的形状和尺寸。

高中数学三视图解题技巧在高中数学中，三视图是一种常见的解题方法，尤其在几何题中应用广泛。

通过三视图，我们可以更加直观地理解和解决问题。

本文将介绍一些常见的三视图解题技巧，并通过具体的题目进行说明，帮助高中学生和他们的父母更好地掌握这一解题方法。

一、什么是三视图三视图是指一个物体或图形从不同方向观察时所得到的三个视图，通常包括俯视图、前视图和侧视图。

通过这三个视图，我们可以全面了解物体或图形的形状和特征，从而解决与其相关的问题。

二、三视图解题的基本步骤1. 确定视图方向：在解题过程中，首先要确定俯视图、前视图和侧视图的方向，通常俯视图在上方，前视图在中间，侧视图在下方。

2. 观察图形特征：通过观察三个视图，分析图形的特征，如边长、角度、对称性等。

3. 建立关系：根据观察到的特征，建立各个视图之间的关系，找出它们之间的联系。

4. 运用几何知识：根据建立的关系，运用几何知识进行推理和计算，解决问题。

三、三视图解题的考点1. 图形的投影：在三视图中，图形的投影是一个重要的考点。

投影是指物体在不同方向上的阴影，通过观察投影，我们可以确定图形的形状和位置。

例如，某题给出了一个正方体的三视图，要求求解正方体的体积。

通过观察侧视图，我们可以发现正方体的高度，然后根据俯视图和前视图中的边长信息，计算出正方体的体积。

2. 图形的对称性：在三视图中，图形的对称性也是一个重要的考点。

通过观察三个视图，我们可以判断图形是否具有对称性，并利用对称性进行计算。

例如，某题给出了一个立方体的三视图，要求求解立方体的表面积。

通过观察俯视图和前视图，我们可以发现立方体的两个相对面是相等的，根据对称性，我们可以利用这个特点计算出立方体的表面积。

3. 图形的位置关系：在三视图中，图形的位置关系也是一个重要的考点。

通过观察三个视图，我们可以确定图形之间的位置关系，并利用位置关系进行计算。

例如，某题给出了一个平行四边形的三视图，要求求解平行四边形的面积。

高中数学立体几何三视图的画法与性质分析在高中数学的学习中，立体几何是一个重要的内容，其中三视图的画法与性质更是需要我们掌握的知识点。

三视图是指一个立体物体从不同方向观察时所得到的正投影图，包括主视图、俯视图和左视图。

本文将介绍三视图的画法和性质，并通过具体例子来说明此题的考点，以帮助高中学生更好地理解和掌握这一知识。

一、三视图的画法三视图的画法主要包括以下几个步骤：1.确定主视图：主视图是指从正面观察立体物体时所得到的投影图。

我们可以选择一个适当的位置和角度来观察立体物体，然后将其投影到一个平面上，得到主视图。

2.确定俯视图：俯视图是指从上方向下观察立体物体时所得到的投影图。

我们可以选择一个适当的位置和角度来观察立体物体，然后将其投影到一个平面上，得到俯视图。

3.确定左视图：左视图是指从左侧观察立体物体时所得到的投影图。

我们可以选择一个适当的位置和角度来观察立体物体，然后将其投影到一个平面上，得到左视图。

需要注意的是，在确定三视图时，我们要保证各个视图之间的相对位置和比例关系是一致的，以便更好地体现立体物体的形状和结构。

二、三视图的性质三视图具有以下几个性质：1.各视图之间的关系：主视图、俯视图和左视图是相互关联的，它们共同构成了一个完整的立体物体的图像。

通过观察三视图，我们可以了解立体物体的各个面的形状和大小。

2.投影关系：三视图是立体物体在不同方向上的投影，它们之间存在一定的投影关系。

例如，在主视图中，立体物体的前面对应俯视图的上方，左面对应左视图的右方。

3.边与面的关系：通过观察三视图，我们可以确定立体物体的各个边和面的位置和形状。

例如，在主视图中，我们可以看到立体物体的前面、后面、左面、右面等。

三、举例说明为了更好地理解和掌握三视图的画法和性质，我们以一个简单的立方体为例进行说明。

首先，我们确定立方体的主视图。

假设我们选择立方体的一个面作为主视图，将其投影到平面上得到主视图。

接下来，我们确定立方体的俯视图。

高考数学中的三视图与投影相关知识点在几何学的领域中，三视图与投影是十分重要的一部分，它们不仅仅是应用于让我们更好地看清三维物体，也是高考数学常见的考点之一。

因此，在这篇文章中，我们将深入探讨高考数学中的三视图与投影相关知识点，帮助大家更好地理解和应用相关内容。

一、三视图概述在现实生活中，很多物体都是三维的，它们有长度、宽度和高度等特征，但我们任何时候都无法同时看到物体的所有信息，因为我们的眼睛只能看到一个角度。

为了更好地看清三维物体，我们可以将其分解为三个不同的投影角度，即正面视图、左视图和顶视图，这就是三视图的概念。

在数学中，我们可以通过三个二维的视图来表示三维物体的形状，三个视图分别呈现物体的正面、左侧和顶部，这些视图给我们提供了关于物体轮廓形状的详细信息。

三维物体的三视图可以通过投影的方式得到，这也是三视图和投影密不可分的原因。

二、投影概述投影是基于投影面和投影线进行的，是将三维物体在二维平面上展示的一种方式。

在投影中，投影面和投影线的位置非常重要，它们决定了最终投影的效果和质量。

在平行投影中，投影线是垂直于投影面的直线，这种投影方式可以得到准确的形状和大小，但是它的透视感比较弱，在某些情况下无法展示物体的深度，因此在我们画高考数学的题目时需要注意使用透视投影来展示物体的深度。

透视投影是一种根据物体在空间中的位置、大小、形状等特征进行的投影方式。

在透视投影中，物体的前方向是远离投影面的方向，反之则是物体的后方向，这种方式可以更好地表现物体的深度和透视效果。

三、三视图和投影的联系三视图和投影密不可分，因为三视图是通过投影方式得到的，我们可以通过三视图来确定物体在三维空间中的位置和方向，从而得到正确的投影。

在绘制三视图时，我们需要利用的是三个视图的交点来确定物体的位置，然后再根据物体的大小和形状来确定它的轮廓。

同样，在投影中，我们也需要确定三维物体在空间中的位置和方向，然后再根据其大小和形状进行投影。

高考数学中的三视图及相关方法在高考数学中，三视图是一个常见的概念。

三视图是一个物体分别从三个不同的方向所观测到的图形，通过三个视图可以确定一个物体的形状、尺寸及空间位置。

在学习三视图时，需要掌握一些相关的知识和方法。

一、投影法与投影面在学习三视图之前，需要先掌握投影法和投影面的相关概念。

投影法是指从物体上某一点出发，将光线对着投影面射出，所形成的投影。

投影面是指用来做投影的平面。

在三视图中，通常使用前、上、侧三个平面来进行投影，这三个平面分别称为主平面。

二、主视图主视图是指在三视图中，以物体的正面朝前、上面朝上、左面朝左的方向所形成的视图。

主视图常常是确定一个物体的形状和尺寸的主要依据。

三、侧视图侧视图是指在三视图中，以物体左侧面朝上、物体正面朝前、物体下侧面朝下的方向所形成的视图。

侧视图和主视图相结合，可以确定一个物体的整体形状和尺寸。

四、俯视图俯视图是指在三视图中，以物体的上部朝上、物体的前面朝下、物体的左侧面朝左的方向所形成的视图。

俯视图主要用来确定一个物体的上部结构，例如天棚、台面等。

五、三视图的绘制方法在学习三视图时，需要掌握三视图的绘制方法。

绘制三视图时，需要确定主平面，然后将物体在主平面上分别绘出主视图、侧视图、俯视图。

在绘制时，需要按比例绘制，保持各个视图之间的比例关系一致。

六、三视图的应用在实际生活中，三视图有很多应用。

例如在工程设计中，可以通过三视图来确定一个建筑物或机械设备的形状和尺寸，以便进行制造和施工。

在家具设计方面，通过三视图可以确定家具的形状和尺寸，以便进行制造和销售。

总之，三视图在数学中是一个非常重要的概念。

通过学习三视图，可以帮助我们更好地了解物体的形状、尺寸和空间位置，从而更好地进行设计、制造和施工。

通过掌握三视图的相关知识和方法，我们可以在高考数学中取得更好的成绩。

高中数学三视图知识点总结及解题技巧专题汇总高中数学三视图知识点总结及解题技巧专题汇总三视图是指物体向投影面投影所得到的图形。

将物体在三个相互垂直的平面内作垂直投影所得的三个图形，称为三视图，分别为主视图（正）、俯视图和侧（左）视图。

正投影是指投影线互相平行，并都垂直于投影面的投影。

识图技巧包括试图位置、侧面与试图的关系、看图要领和选取的几何体。

一般三视图的放置方式是按照标准位置，便于尺寸的对应。

当几何体的侧面与投影面不平行时，该侧面的视图形状不是真实的形状，只有当侧面与投影面平行时，视图才能真实地反映几何体侧面的形状。

在看图时，主、俯视图长对正；主、侧视图高平齐；俯、侧视图宽相等。

在三视图考题中，选取的几何体一般有三种，包括常见的几何体、被平面截取后得到的几何体和组合体。

解题要领包括先确定底面、找视图中有线线垂直的地方和注意三视图与几何体的摆放位置直接相关。

大多数试题中下、俯视图的图形都是几何体底面的真实形状。

关键线往往对应着几何体中线面垂直、面面垂直的地方。

几何体的高很多情况就是视图平面图形的高，求几何体的体积时这一点显得尤为重要。

同样一个几何体若摆放位置不同，那么三视图的形状也会有变化。

典型例题讲解：某几何体的三视图如下，确定它的形状。

通过分析俯视图，可以知道底面是直角三角形；通过主视图，可以确定SA在几何体中是一条与底面垂直的棱。

重新画出三视图，放到标准位置，方便长度关系的计算。

由对应关系，可以算得底面三角形的高应为2，故底面的面积为4.高为2，则体积为18/3=6.综上所述，了解三视图的概念和识图技巧，掌握解题要领和典型例题的解法，能够有效提高解决三视图问题的能力。

已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是多少？分析：1）看俯视图，确定底面为一个正方形。

2）看正视图和俯视图，最右边应该垂直于底面，且与底面垂直的是一个三角形的面。

3）这样就可以确定了，这个几何体是一个四棱锥，底面是正方形，一个侧面是等腰三角形且与底面垂直。

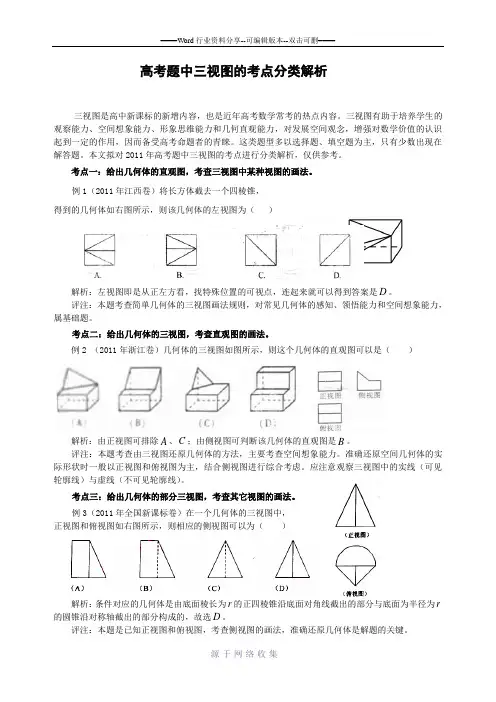
高考题中三视图的考点分类解析三视图是高中新课标的新增内容，也是近年高考数学常考的热点内容。

三视图有助于培养学生的观察能力、空间想象能力、形象思维能力和几何直观能力，对发展空间观念，增强对数学价值的认识起到一定的作用，因而备受高考命题者的青睐。

这类题型多以选择题、填空题为主，只有少数出现在解答题。

本文拟对2011年高考题中三视图的考点进行分类解析，仅供参考。

考点一：给出几何体的直观图，考查三视图中某种视图的画法。

例1（2011年江西卷）将长方体截去一个四棱锥，得到的几何体如右图所示，则该几何体的左视图为（）解析：左视图即是从正左方看，找特殊位置的可视点，连起来就可以得到答案是D。

评注：本题考查简单几何体的三视图画法规则，对常见几何体的感知、领悟能力和空间想象能力，属基础题。

考点二：给出几何体的三视图，考查直观图的画法。

例2 （2011年浙江卷）几何体的三视图如图所示，则这个几何体的直观图可以是（）解析：由正视图可排除A、C；由侧视图可判断该几何体的直观图是B。

评注：本题考查由三视图还原几何体的方法，主要考查空间想象能力。

准确还原空间几何体的实际形状时一般以正视图和俯视图为主，结合侧视图进行综合考虑。

应注意观察三视图中的实线（可见轮廓线）与虚线（不可见轮廓线）。

考点三：给出几何体的部分三视图，考查其它视图的画法。

例3（2011年全国新课标卷）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（）解析：条件对应的几何体是由底面棱长为r的正四棱锥沿底面对角线截出的部分与底面为半径为r 的圆锥沿对称轴截出的部分构成的，故选D。

评注：本题是已知正视图和俯视图，考查侧视图的画法，准确还原几何体是解题的关键。

考点四：给出几何体的三视图，考查原几何体的表面积、体积及相关计算问题等。

例4 （2011年安徽卷）一个空间几何体得三视图如图所示，则该几何体的表面积为（ ）（A ）48（B ）32+817（C ）48+817（D ）80解析：由三视图可知几何体是底面是等腰梯形的直棱柱。

高二数学三视图知识点三视图是指一个立体物体在空间中分别从正面、侧面和顶视图的观察。

它是工程图学中的重要内容之一，也是解决物体表面形貌和内部结构的有效手段之一。

在高二数学中，学生需要掌握三视图的基本概念、表示规则和绘制方法。

本文将详细介绍高二数学中与三视图相关的知识点。

1. 什么是三视图三视图是对一个立体物体在三个不同方向上的投影。

它分别包括正视图、侧视图和俯视图。

正视图是物体与观察者距离垂直的方向上的投影，侧视图是物体与观察者平行的方向上的投影，俯视图是物体从上方向下看的投影。

2. 三视图的表示规则为了准确表示立体物体的形状和尺寸，三视图需要遵循一定的表示规则。

具体来说，三视图的表示规则包括以下几点：(1) 三视图应该相互平行，即它们的投影线应该平行而不交叉。

(2) 三视图应该共享相同的中心线，这样可以保证它们在空间中的位置对应正确。

(3) 三视图的尺寸应该相互关联，即它们的尺寸应该按照比例关系绘制。

3. 三视图的绘制方法在绘制三视图时，首先需要确定图纸上的比例尺。

然后，按照投影关系和比例关系，分别绘制正视图、侧视图和俯视图。

具体绘制方法如下：(1) 正视图：从物体的正面观察，按照比例标注物体的尺寸和形状。

通常将正视图放在图纸的左侧，方便观察和理解。

(2) 侧视图：从物体的侧面观察，按照比例标注物体的尺寸和形状。

通常将侧视图放在正视图的右侧。

(3) 俯视图：从物体的上方观察，按照比例标注物体的尺寸和形状。

通常将俯视图放在图纸的底部。

4. 三视图的应用三视图在工程图学中有广泛的应用。

首先，三视图可以用来描述和表达立体物体的形状和结构，方便设计和制造。

其次，三视图可以用来解决空间几何问题，如平行和垂直关系的判断。

此外，三视图还可以用来展示和分析建筑、机械和电路等领域的具体问题。

总结：高二数学中的三视图知识点包括三视图的基本概念、表示规则和绘制方法。

通过掌握三视图的原理和技巧，可以有效地解决立体物体的表面形貌和内部结构问题。

People who have never failed may not have succeeded either.（页眉可删）高中三视图的解题技巧空间立体几何的三视图是高中数学新课程的新增内容之一，也是近几年全国各地高考的热点内容，那你知道高中三视图有什么解题技巧吗?下面是整理的高中三视图的解题技巧的相关内容，仅供参考。

高中三视图的解题技巧【1】一、简单几何体的三视图还原规律复杂的几何体是由简单几何体组合而成的,简单几何的分类:柱体(圆柱和棱柱);椎体(圆锥和棱锥);台体(圆台和棱台);球体.要掌握复杂几何体的三视图还原,先要搞清楚简单几何体的三视图还原规律,一般情况下简单几何体的三视图还原有如下规律：1. 三视图中如果其中两个视图是矩形(不要管内部的细节,只要外轮廓线为矩形就称该视图为矩形)那么该空间几何体为柱体.当第三个试图为圆时,该空间几何体为圆柱，否则为棱柱.2. 三视图中如果其中两个视图是三角形(不要管内部的细节,只要外轮廓线为矩形就称该视图为三角形)那么该空间几何体为锥体,当第三个试图为圆时,该空间几何体为圆锥,否则为棱锥.3. 三视图中如果其中两个视图是梯形(不要管内部的细节，只要外轮廓线为矩形就称该视图为梯形)那么该空间几何体为台体.当第三个试图两个同心圆时,该空间几何体为圆台,否则为棱台.二、叠加式组合体的三视图还原方法组合体的组合形式可分为三种:叠加式、切割式、综合式.切割式与综合式在高中阶段见到的不是很多,这里只对高中阶段出现较多的叠加式组合体的三视图还原方法进行论述.既然组合体是由简单几何体组合而成的,那么就可以“化整为零”,把组合体的三视图划分为一个个简单几何体的三视图,再分别根据这些简单几何体的三视图按照上面论述的简单几何体三视图的还原规律把它们还原成简单几何体,再“积零为整"，把这些简单几何体组合在一起就得了组合体的三视图.这样就将复杂的三视图问题转化成最基本的'简单几何体的三视图还原问题来解决了,大大降低了对空间想象能力的要求,这一方法的难点在于如何把组合体的三视图划分为一个个简单几何体的三试图,该方法的具体过程如下：1. 分线框.一般从主视图入手,将主视图划分成一个个线框(一般是封闭的线框，但有时也可不完全封闭),这些线框就是组成组合体的一个个简单几何体的主视图.2. 对投影.在俯视图和左视图上把主视图中每个线框对应的投影找出来,主要是根据“长对正,高平齐,宽相等”和"三视图所反映的组合体各部分的方位”来找.3. 识形体.根据每一部分的三视图,逐个想象出每一部分所对应的几何体4. 合起来,想整体. 每一部分的形状确定后,再根据各部分的相对位置关系组合成整个组合体的形状.相关阅读-高中三视图规则【2】主俯长对正、主左高平齐、俯左宽相等即:主视图和俯视图的长要相等主视图和左视图的高要相等左视图和俯视图的宽要相等。

高考三视图知识点高考是每个学生都将面临的一次重要考试。

其中，物理学科对于很多学生来说可能是一个难点。

而在物理学中，三视图是一个重要的知识点，需要学生掌握和理解。

本文将重点介绍高考物理中的三视图知识点，从不同角度深入讨论，帮助学生更好地理解和应对考试。

一、什么是三视图？三视图是指一个物体在不同方向上的投影图。

通常来说，我们可以通过正视图、左视图和俯视图来理解一个物体的形状和结构。

正视图是指从物体正前方看的投影图，左视图是指从物体左侧看的投影图，俯视图是指从物体上方看的投影图。

二、三视图的应用三视图在日常生活和工程设计中有着广泛的应用。

在建筑设计中，工程师需要通过三视图来理解和描述建筑物的形状和结构，从而进行合理的设计和施工。

在机械加工中，工人需要通过三视图来理解和操作机械设备，保证产品的准确加工。

在电子电路设计中，工程师需要通过三视图来理解和布局电路板的组成部分，确保电子设备的正常工作。

三、如何绘制三视图？绘制三视图需要一定的技巧和方法。

首先，我们需要确定物体的主视图，即选择一个合适的方向作为正面。

然后，根据物体的形状和尺寸，我们可以绘制正视图和左视图。

在绘制正视图时，需要注意保持比例和准确度，确保投影图能够准确地反映物体的形状和结构。

在绘制左视图时，需要将物体按照一定角度倾斜，以获得合适的投影图。

最后，通过观察和分析正视图和左视图，我们可以绘制出俯视图，从不同角度全面地了解物体。

四、三视图与三维几何的关系三视图是三维几何的重要组成部分，可以通过观察三视图来判断物体的形状和结构。

在三维几何中，我们通过描述物体的点、线和面来构建物体的形态。

而三视图则通过将这些点、线和面在不同方向上投影到二维平面上来描述物体。

因此，三视图可以看作是三维几何与二维平面之间的桥梁，帮助我们理解和描述三维物体。

五、常见的三视图题型在高考物理中，三视图经常出现在选择题和计算题中。

例如，考生可能会遇到给定一个物体的正视图和俯视图，需要根据给定信息绘制出左视图的题目。

高考有方法——三视图解题超级策略一、三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线表示，不能看到的部分用虚线表示．(2)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合．(3)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，123例1A．答案解析ABCD，＝2，在Rt△例2：边长为4，宽为3 的直角三角形，求三棱锥的表面积或体积.跟踪训练5.如图所示为三棱锥的三视图，三视图是直角边长为4等腰直角三角形，虚线为中线，求三棱锥的表面积或体积.方法三三线交汇得顶点法例3：如图，网格纸上小正方形的边长为4，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度是（）A．B．6 C．D．4正确答案是B．解：由三视图可知，原几何体的长、宽、高均为4，所以我们可用一个正方体作为载体对三视图进行还原．先画出一个正方体，如图（1）：第一步，根据正视图，在正方体中画出正视图上的四个顶点的原象所在的线段，这里我们用红线表示．如图（2），即正视图的四个顶点必定是由图中红线上的点投影而成的．第二步，侧视图有三个顶点，画出它们的原象所在的线段，用蓝线表示，如图（3）．第三步，俯视图有三个顶点，画出它们的原象所在的线段，用绿线表示，如图（4）．最后一步，三种颜色线的公共点（只有两种颜色线的交点不行）即为原几何体的顶点，连接各顶点即为原几何体，如图（5）．至此，易知哪条棱是最长棱，求出即可跟踪训练6.首先在正方体框架中描出主视图，并将轮廓的边界点平行延长，如图．类似地，将俯视图和侧视图也如法炮制．这样就可以找到三个方向视123A 4A 、3 B 、3 C 、3D 、2 5、一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（ ）D （B ）71 （C ）61 （D ）51 61（表示1cm ）,图中粗线画出的是某零件的三视图，该零件由一个底面） C59 C. 1027 D. 13D D 11B 17、一个四面体的顶点在空间直角坐标系O xyz-中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0)，画该四面体三视图中的正视图时，以zOx平面为投影面，则得到正视图可以为（）A(A) (B) (C) (D)8、如图，网格纸上小正方形的边长为1910、某几何体的三视图如图所示，则该几何体的体积为_____________.11、已知某几何体的三视图如图所示，则其体积为_____________.20或1612、若某几何体的三视图如图所示，则这个几何体中最长的棱长等于_____________.13、某几何体的三视图如图所示，则该几何体的体积为_____________.1415（A16A.17.A．x(1,1,0) 338 3 32 3。

三视图在高考数学中的应用高考数学中的几何分数占据了相当大的比重，而在几何分数中，三视图是一项重要的知识点。

三视图是指通过底视图、俯视图和左视图三个视图来描述一个物体的形状和结构。

在现代设计制图中，三视图已经成为一种标准的表达方式，被广泛应用于工程制图、建筑设计等领域。

在高考数学中，对三视图的掌握也显得至关重要。

一、三视图的概念和作用三视图是指通过底视图、俯视图和左视图三个视图来描述一个物体的形状和结构。

底视图、俯视图、左视图分别是从下方、从上方、从左侧看到的物体的真实图样。

三视图可以准确地表现一个物体的三个面，从而全面地反映该物体的形状和结构。

三视图在工程制图和建筑设计中应用广泛，可以帮助设计师更加直观地了解物体的结构、尺寸和位置关系，从而更好地完成设计任务。

在高考数学中，三视图的作用更多体现在几何分数的考核中，通过掌握三视图的相关知识，可以更好地完成几何分数的解答。

二、三视图的基本性质和特点1. 三视图的数量相同由于底视图、俯视图和左视图分别描述一个物体的不同部分，因此它们的数量是相同的。

在制图和解题中，必须同时绘制或使用三个视图，以确保图形的准确性和完整性。

2. 三视图互相独立在三视图中，底视图、俯视图和左视图是彼此独立的，它们所描述的面也是互不相同的。

因此，在使用三视图解题时，必须注意各个视图之间的关系，确保计算的准确性。

3. 三视图分别包含物体的不同面底视图、俯视图和左视图分别描绘物体的下侧、上侧和侧面。

底视图描绘的是物体的下半部分，俯视图描绘的是物体的上半部分，左视图描绘的是物体的左半部分。

三、三视图的相关知识点和计算方法1. 三视图的绘制方法底视图、俯视图和左视图的绘制方法类似，在绘制过程中需要注意以下几点：构图在绘制三视图时，应该首先确定物体的正面和方向，根据实际情况选择合适的画纸大小和比例，并合理使用绘图工具和比例尺，以确保图形的准确性。

投影在绘制三视图时，需要进行投影，即通过垂直于某个面的平面来将该面的形状投影到纸面上。

高中数学三视图绘制与构造方法解析在高中数学中，三视图绘制是一个重要的内容，它与几何图形的认识、空间想象力以及工程制图等领域密切相关。

本文将对高中数学三视图绘制的基本概念、构造方法和解题技巧进行详细解析，帮助高中学生和他们的父母更好地理解和掌握这一知识点。

一、基本概念三视图是指一个立体图形在三个相互垂直的平面上的投影图。

通常将这三个平面分别称为主视图、俯视图和左视图。

主视图是从正面观察立体图形，俯视图是从上方观察立体图形，左视图是从左侧观察立体图形。

通过绘制这三个视图，我们可以全面地了解一个立体图形的形状和结构。

二、构造方法1. 主视图的绘制主视图是从正面观察立体图形，因此我们需要找到一个与主视图垂直的平面。

一种常用的方法是将立体图形放置在一个透明的立方体中，然后在透明立方体的正面上绘制主视图。

例如，我们考虑一个正方体，边长为a，我们可以在一个平面上绘制一个边长为a的正方形作为主视图。

2. 俯视图的绘制俯视图是从上方观察立体图形，因此我们需要找到一个与俯视图垂直的平面。

一种常用的方法是将立体图形放置在一个透明的立方体中，然后在透明立方体的上方绘制俯视图。

例如，我们考虑一个长方体，长为a，宽为b，高为c，我们可以在一个平面上绘制一个长为a，宽为b的长方形作为俯视图。

3. 左视图的绘制左视图是从左侧观察立体图形，因此我们需要找到一个与左视图垂直的平面。

一种常用的方法是将立体图形放置在一个透明的立方体中，然后在透明立方体的左侧绘制左视图。

例如，我们考虑一个长方体，长为a，宽为b，高为c，我们可以在一个平面上绘制一个长为c，宽为b的长方形作为左视图。

三、解题技巧1. 利用已知条件确定立体图形的形状和尺寸在解题过程中，我们通常会给出一些已知条件，如立体图形的体积、表面积或者某些边长、角度等信息。

我们可以利用这些已知条件来确定立体图形的形状和尺寸，从而更好地进行三视图的绘制。

2. 利用投影关系确定三视图之间的位置关系在绘制三视图时，我们需要注意不同视图之间的位置关系。

高二通用三视图知识点在机械设计与制造、建筑设计等领域中，三视图是一种常用的图纸表达形式。

作为高二学生，了解和掌握三视图的知识点对于将来的学习和职业发展都具有重要意义。

本文将介绍高二通用三视图的相关知识点，包括三视图的概念、构图要点以及常见图形的三视图表达方法等。

一、三视图的概念三视图是指一个物体或者一个构件从不同视角观察时得到的三个不同的视图，分别是俯视图、前视图和右视图。

俯视图是以物体的顶面朝下观察得到的视图，前视图是以物体的正面朝观察得到的视图，右视图是以物体的右侧朝观察得到的视图。

三视图可以全面地展示一个物体的外形尺寸和结构特点，为设计和制造提供重要的参考依据。

二、构图要点1. 视图的位置关系：在绘制三视图时，需要确保三个视图之间的位置关系是准确的。

一般来说，前视图位于俯视图的下方，右视图位于前视图的右侧。

三个视图需要保持相互垂直的关系，在绘制过程中要仔细测量和标注尺寸。

2. 画线和标注：绘制三视图时，需要使用各种线型来勾画物体的轮廓和内部特征。

常用的线型包括实线、虚线、粗线和细线等。

绘制过程中应注意线条清晰、精确，并标注尺寸和特征以便后续的设计和制造工作。

3. 隐藏线的处理：在绘制三视图时，有些线条是表示物体内部的轮廓或特征，需要使用虚线或者隐藏线的方式进行标注。

隐藏线的处理要根据物体的结构和视图的需求进行，以准确表达物体的形状和特征。

三、常见图形的三视图表达方法1. 立方体：立方体是最基础的图形之一，它的三视图包括俯视图是一个正方形、前视图也是一个正方形，右视图是一个长方形。

在绘制立方体的三视图时，需要注意各个视图之间的尺寸关系和比例。

2. 圆柱体：圆柱体是由底面圆和侧面矩形组成的，其三视图包括俯视图是一个圆、前视图是一个矩形，右视图是一个长方形。

在绘制圆柱体的三视图时，需要准确表达底面圆和侧面矩形的轮廓和尺寸。

3. 锥体：锥体是由底面圆和侧面三角形组成的，其三视图包括俯视图是一个圆、前视图是一个三角形，右视图是一个三角形。

三视图高考题解题技巧
三视图高考题解题技巧
1、主视图和左视图如果都是三角形的必然是椎体，要么是棱锥要么是圆锥。

还有两种特殊的情况：
1、是棱锥和半圆锥的组合体。

2、就是半圆锥。

到底如何如确定就是通过俯视图观察。

(1) 若俯视图是三角形时，就是三棱锥。

(2) 若俯视图是多边形时，就是多棱锥。

(3) 若俯视图是半圆和三角形时，就是是棱锥和半圆锥的组合体。

(4) 若俯视图是半圆时，就是半圆锥。

(5) 注意虚线和实线的意义，虚线代表的是看不到的线，实线代表的是能看的见得都是一种平行投影所创造出来的。

2、三视图求体积时候，先观察主视图和侧视图，注意主视图和侧视图的高一定都是一样的，并且肯定是立体图形的高，先通过观察判定图形到底是什么立体图形，看看到底是棱锥，棱柱，还是组合体，通常的组合体都是较为简单的.组合体，无需过多考虑。

(1) 如果是棱锥的话，就看俯视图是什么图形，判定后算出俯视图的面积即可，应用体积公式。

(2) 如果是棱柱的话，同样看俯视图的图形，求出面积，应用公式即可。

(3) 如果是组合体，要分辨出是哪两种规则图形的组合，分别算出体积相加即可。