当前位置：文档之家 › 工程光学习题解答--第二章-理想光学系统

工程光学习题解答--第二章-理想光学系统

  • 格式：doc
  • 大小：502.00 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

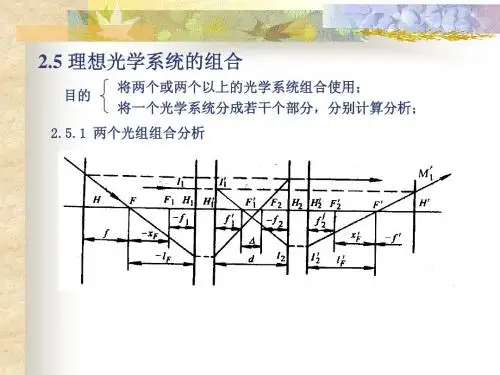
2理想光学系统2

2理想光学系统2

h2 175 tgu 2 ' = tgu 2 + = −0.25 + = 0.1 f2 ' 500 h2 175 100 lF = = = 1750mm ∴ f '= = 1000mm tgu 2 ' 0.1 0. 1
物方焦点位于第一面左1750mm处 而焦距为1000mm， 物方焦点位于第一面左1750mm处，而焦距为1000mm，所以主面位 1750mm 1000mm 于第一面左750mm 750mm处 于第一面左750mm处。
xF
f1 f1 ' xF = ∆
注意： 注意： x F 为F1与 F之间距离
x F < 0 则F在F1左侧
组合光组的 焦距
H'F' M'H' = 像方焦距： ⊿M’F H ∽⊿I H F 像方焦距： ⊿M F’H’∽⊿I2’H2’F’ → F'H2 ' H2 'I2 '
I 1 ' H 1 ' H 1 ' F1 ' = ⊿I2H2F1’∽⊿I1’H1’F1 → ∽⊿I H F H2I2 F1 ' H 2
n −1 dρ1 透镜组像方主面到第二面主面的距离 主面位置： 主面位置： l H ' = − f '⋅ n n −1 lH = − f ' dρ 2 透镜组物方主面到第一面主面的距离 n
结论： 透镜结构参数r 结论： 透镜结构参数r1，r2，d，n决定光学性能 f（焦距） 焦距） 物像方主面位置） l H , l H ' （物像方主面位置）
H ' F ' H 1 ' F1 ' = 所以 F ' H 2 ' F1 ' H 2

工程光学2-2

工程光学2-2

第四节 里想光学系统的放大率
一、垂轴放大率
第二章 理想光学系统
y′ f x′ l ′f β = =− =− =− y x f′ lf ′
1.微小位移时的 α
f =− f ′
l′ = l
二、轴向放大率
xx ' = ff '
⇒ xdx ' + x ' dx = 0
dx ' dl ' α = = dx dl
若物空间与像空间的介质折射率相等 n=n'
f =−f′
β =
l' l
四 理想光学系统两焦距之间的关系
第二章
理想光学系统
∵ (−l )tg (−u ) = ltgu = l ′tgu ′ = h ∵ −( x + f )tg (−u ) = ( x + f )tgu = ( x′ + f ′)tgu ′…… (1) ′ y′ f x′ fy f y′ ∵ β = = − = − ⇒ x = − ; ; x′ = − 带入（1 ）式得： y x f′ y′ y ′ ′ fytgu = − f y′tgu ′ ∵ tgu ≈ u ⇒ fyu = − f y′u ′ ∵ nyu = n′y′u ′ f′ n′ ∴ = − ; 当n = n ′ ⇒ f ′ = − f f n
解：这是个两次成像的问题，设对L1的物距、像距分别为l1和l1′ ′ 对L 2为l2 和l2 , 注意l2 = (l1′ − d ), 则由高斯公式： 1 1 1 1 1 1 − = ⇒ − = l1′ l1 f1′ l1′ −10 5 1 1 1 1 1 1 1 1 1 − = ⇒ − = ⇒ − = ′ ′ ′ l 2 l2 f 2′ l2 (l1′ − d ) f 2′ l2 (l1′ − 5) −10 ′ ⇒ l1′ = 10.00cm; l2 = −5.00cm; l2 = 10.00cm ′ l1′ l2 10 10 β1 = − = − = −1.00; β 2 = − = − = 2.00 l1 10 −5.0 l2

工程光学第二章练习参考答案

工程光学第二章练习参考答案

(5)
n sinU NA sinU 0.1
U 5.73917 D 2( ltgU ) 2(45 tg 5.73917 ) 9.045mm
(5)
lz 160 D D' 1.667 9.00mm lz ' 29.63
(6)
-l (6)
l’ 180 -lz
h3 h2 d 2 tgu2 ' 12 10 0.04 11.6 tgu3 ' tgu3 h3 11.6 0.04 0.156 f3' 100
第二章 17
F’ 求物方参数。反向算。 h1=10
H’
u3’
f’
h1 10 f ' 64.102564 tgu3 ' 0.156 h3 11.6 lF ' 74.35897 tgu3 ' 0.156
第二章 17
求物方参数。反向算。
h1=10
H’
u3’
F’
f1 ' 50, f 2 ' 50, f 3 ' 100 d1 d 2 10
f’
lF’
tgu1 ' tgu2
h1
f1 '
10
50
0.2
h2 h1 d1tgu1 ' 10 10 ( 0.2) 12 tgu2 ' tgu3 tgu2 h2 f2' 0.2 12 50 0.04
第二章 ３
y H -f d 1140mm 7200mm H’ f’ y’
l ' l 10
l d l ' 7200 2 f ' d 1140 1 1 1 l' l f'

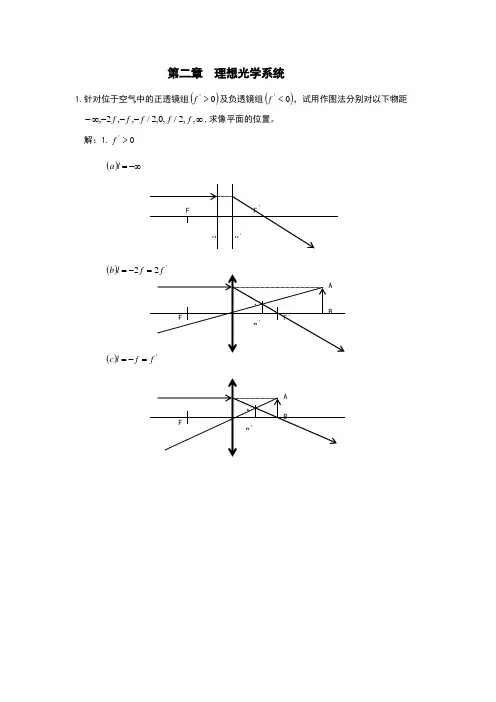
工程光学习题参考答案第二章理想光学系统

工程光学习题参考答案第二章理想光学系统

第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ，试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。

解：1.0'>f ()-∞=l a()'2f l b -=()f f l c =-=()/f l d -=()0=l e()/f l f =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’＝75mm,被摄景物位于（以F 点为坐标原点）=x ,2,4,6,8,10,m m m m m -----∝-处，试求照相底片应分别放在离物镜的像方焦面多远的地方。

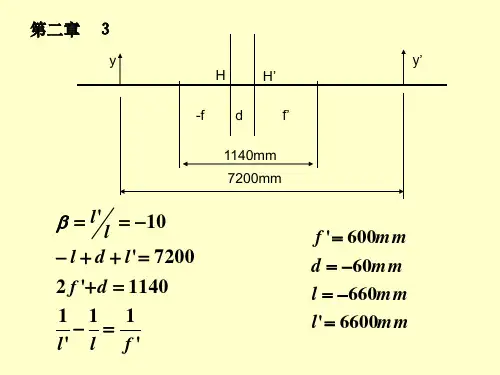
解： （1）x= -∝ ，xx ′=ff ′ 得到：x ′=0 （2）x ′= （3）x ′= （4）x ′= （5）x ′=（6）x ′=3.设一系统位于空气中，垂轴放大率*-=10β，由物面到像面的距离（共轭距离）为7200mm ， 物镜两焦点间距离为1140mm 。

求该物镜焦距，并绘出基点位置图。

解:∵ 系统位于空气中，f f -='10''-===ll y y β 由已知条件：1140)('=+-+x f f7200)('=+-+x l l解得：mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上，当透镜向物体移近18mm 时，物体将被放大*-4，试求透镜的焦距，并用图解法校核之。

解：方法一：31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二： 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三： 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像，放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上，则见像向透镜方向移动，放大率为原先的3/4倍，求两块透镜的焦距为多少 解：⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像，像高为物高的一半，今将物面向物体移近100mm ， 则所得像与物同大小，求该正透镜组的焦距。

工程光学基础教程-习题答案(完整)

工程光学基础教程-习题答案(完整)

第一章 几何光学基本定律1. 已知真空中的光速c ＝3810⨯m/s ，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s, 当光在火石玻璃中，n ＝1.65时，v=1.82 m/s ， 当光在加拿大树胶中，n=1.526时，v=1.97 m/s ， 当光在金刚石中，n=2.417时，v=1.24 m/s 。

2. 一物体经针孔相机在 屏上成一60mm 大小的像，若将屏拉远50mm ，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x ，则可以根据三角形相似得出：,所以x=300mm即屏到针孔的初始距离为300mm 。

3. 一厚度为200mm 的平行平板玻璃（设n =1.5），下面放一直径为1mm 的金属片。

若在玻璃板上盖一圆形的纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片的最小直径应为多少？2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ，包层的折射率为2n ，光纤所在介质的折射率为0n ，求光纤的数值孔径（即10sin I n ，其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有： n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上，求其会聚点的位置。

工程光学第02章

工程光学第02章
(2) 垂直于光轴的平面物与其共轭平面像的几何形状完全相似，即： 在垂直于光轴的同一平面内，物体各部分具有相同的放大率β。 相同放大率处，只有唯一确定的位置与其对应。
(3) 一个共轴理想光学系统，如果已知两对共轭面的位置和放大率， 或者一对共轭面的位置和放大率，以及轴上两对共轭点的位置，则 其它一切物点的共轭像点都可以根据这些已知的共轭面和共轭点来 表示。
（2）实例
① 轴外点 ② 轴上点：（方法一，方法二） ③ 轴上点经两个光组
B’
A
H’
F
H
F’
A’
B
① 过物方焦点的光线，经系统后平行于光轴； ② 平行于光轴的入射光线，经系统后过像方焦点。
（2）实例
① 轴外点 ② 轴上点：（方法一，方法二） ③ 轴上点经两个光组
A
H’
A’
A
F
H F’
xx' f f' （牛顿公式）
（2）高斯公式 以主点为坐标原点，来规定物（像）位置： • 主点→物（像）与光传播方向一致，为（+） • 物距用 l 表示，像距用 l ’ 表示
f f' l l' 1
（高斯公式）
※① 牛顿公式推导：
M
M’
B’
y’
A
H’
-y
F
H
F’
A’
B
N
N’
-x
-f
f’
x’
-l
l’
• 平均轴向放大率： 定义—— x' x2' x1'
x x2 x1
x'f'ff'ff'fx2x1
x2 x1
x1x2
x f 1 x '2 f f f' x f 1 x f 2 f f' 12 n n ' 12

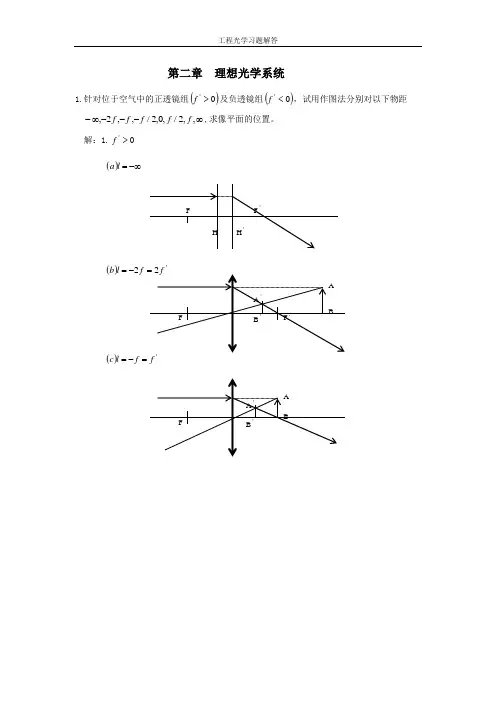
工程光学习题解答--第二章-理想光学系统

工程光学习题解答--第二章-理想光学系统

第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ，试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。

解：1.0'>f ()-∞=l a()'2f l b -=()f f l c=-=()/f l d -=()0=l e()/f lf =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’＝75mm,被摄景物位于（以F 点为坐标原点）=x ,2,4,6,8,10,m m m m m -----∝-处，试求照相底片应分别放在离物镜的像方焦面多远的地方。

解： （1）x= -∝ ，xx ′=ff ′ 得到：x ′=0 （2）x ′=0.5625 （3）x ′=0.703 （4）x ′=0.937 （5）x ′=1.4（6）x ′=2.813.设一系统位于空气中，垂轴放大率*-=10β，由物面到像面的距离（共轭距离）为7200mm ， 物镜两焦点间距离为1140mm 。

求该物镜焦距，并绘出基点位置图。

解:∵ 系统位于空气中，f f -='10''-===ll y y β 由已知条件：1140)('=+-+x f f7200)('=+-+x l l解得：mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上，当透镜向物体移近18mm 时，物体将被放大*-4，试求透镜的焦距，并用图解法校核之。

解：方法一：31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二： 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三： 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像，放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上，则见像向透镜方向移动，放大率为原先的3/4倍，求两块透镜的焦距为多少？ 解：⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像，像高为物高的一半，今将物面向物体移近100mm ， 则所得像与物同大小，求该正透镜组的焦距。

理想光学系统

理想光学系统

第三节 理想光学系统的物像关系
几何光学的基本内容之一是求像，即对于确定的 光学系统，给定物体的位置、大小、方向，求像的位 置、大小、正倒及虚实。常用的用以求取物象位置关 系的方法有二种：一为图解法，一为解析法。 一、图解法求像
图解法求像的定义
已知一个光学系统的主点(主面)和焦点的位置， 利用光线通过这些基点后表现的性质，对物空间给 定的点、线和面，通过画图追踪典型光线的方法求 像。
工程光学
石家庄铁道大学
机械工程学院
总第三讲
第二章 理想光学系统
Perfect Optical System

光学系统的具体结构（r、d、n） 实际光学系统与高斯（近轴）光学系统 研究光学系统成像的目的在于将高斯光学 完善成像的理论推广到任意大的空间，本 章的主要内容即介绍建立在高斯光学之上 的所谓理想光学系统，并研究理想光学系 统的主要光学参数、成像关系、放大率以 及光组组合和透镜。
可选择的典型光线和可利用的性质： ①平行于光轴入射的光线，经系统后过像方焦点； ②过物方焦点的光线，经过系统后平行于光轴； ③倾斜于光轴入射的平行光束经过系统后会交于像 方焦平面上的一点； ④自物方焦平面上一点发出的光束经系统后成倾斜 于光轴的平行光束； ⑤共轭光线在主面上的投射高度相等。 欲在理想光学系统条件下确定像点位置，只需 求出其对应物点发出的两条特定光线在像空间的共 轭光线，其交点即为所求像点。
总第三讲
３、主点与主平面
Q
Q'
h
f
'
h tanU '
F
U
H
H'
U
'
h'
F'
f
h tan U

工程光学(知识讲座)

工程光学(知识讲座)

工程光学第二章理想光学系统1、一个折射率为1.52的双凸薄透镜，其中一个折射面的曲率半径是另一个折射面的2倍，且其焦距为5cm，则这两个折射面的曲率半径分别是〔7.8〕cm和〔-3.9〕cm。

2、一个薄透镜折射率为1.5，光焦度500D。

将它浸入某液体，光焦度变成-1.00D，则此液体的折射率为〔1.502〕。

3、反远距型光组由〔一个负透镜和一个正透镜〕组成，其特点是〔工作距大于组合焦距〕。

4、远摄型光组由一个〔正透镜〕和一个〔负透镜〕组成，其主要特点是〔焦距大于筒长〕，因此该组合系统常用在〔长焦距镜头〕的设计中。

第三章平面与平面系统1、反射棱镜在光学系统中的主要作用有〔折叠光路〕、〔转折光路〕和转像、倒像等，在光路中可等效为平行平板加〔平面反射镜〕。

2、某种波长的光入射到顶角为60°的折射棱镜，测得最小偏向角为42°15′，则该种玻璃对于入射波长的折射率为〔1.557〕。

3、唯一能完善成像的光学元器件是〔平面反射镜〕，利用其旋转特性可制作光学杠杆进行放大测量；利用双光楔也可以实现〔微小角度和微小位移〕的测量，主要有〔双光楔旋转测微〕和〔双光楔移动测微〕两种形式。

4、用于制作光学元件的光学材料包括光学玻璃，〔光学晶体〕和〔光学塑料〕三类。

选用光学玻璃时的两个重要参数是〔折射率〕和〔阿贝常数〕。

5、一个右手坐标的虚物，经一个直角屋脊棱镜反射后，成〔右手〕坐标的〔虚〕像。

第四章光学系统中的光束限制1、限制轴上物点成像光束宽度的光阑是〔孔径光阑〕，而〔渐晕光阑〕在其基础上进一步限制轴外物点的成像光束宽度。

2、为减少测量误差，测量仪器一般采用〔物方远心〕光路。

3、测量显微镜的孔径光阑放置在〔物镜后焦平面上〕，视场光阑放置在〔一次实像面处〕，如果用1/2″的CCD接收图像并用14″的监视器观察图像，要求系统放大倍率为140倍，则显微镜的放大倍率是〔5倍〕。

第五章光线的光路计算及像差理论1、实际像与〔理想像〕之间的差异称为像差，包括单色像差和色差两大类。

大学工程光学第二章.

大学工程光学第二章.

2. 角放大率——像方、物方倾斜角的正切之比
若 n'=n
2.4物像位置和Βιβλιοθήκη 种放大率、两种焦距和光焦度 工 程 光 学 3. 对薄凸透镜，几个特殊位置的 β、α、γ
（1） 物在无穷远，像与像方焦点重合
（2）物在2倍物方焦距处，像为等大倒立的实像
2.4物像位置和三种放大率、两种焦距和光焦度 工 程 光 学 （3）物与物方焦面重合时
2.4物像位置和三种放大率、两种焦距和光焦度 工 程 光 学 二、理想光学系统两焦距的关系和拉氏公式
l tanU h l ' tanU ' ( x f ) tanU ( x' f ' ) tanU '
y xf y' y' x' f ' y
fy tanU f ' y ' tanU ' fyu f ' y ' u ' nyu n' y ' u '
f' n' f n
2.4物像位置和三种放大率、两种焦距和光焦度 工 程 光 学
f' n' f n
若 n‘=n,则f = -f’得：
y' x' f l' f y f' x l f'
xx' f ' f' x' l ' x f' l
2
1 1 1 l' l f '
2.1 理想光学系统 2.1 理想光学系统 2.2 理想光学系统的基点和基面
工程光学
2.3 物像位置和三种放大率、两种焦距和光焦度

工程光学基础 习题参考答案-第二章_02

工程光学基础 习题参考答案-第二章_02

3、设一系统位于空气中， 设一系统位于空气中，垂轴放大 率 β = −10 × ， 由物面到像面的距离 （共轭距） 共轭距）为 7200mm，物镜两焦点 间距离为 1140mm。求该物镜焦距， 求该物镜焦距， 并绘出基点位置图。 并绘出基点位置图。 解： 由公式 β = − x' f = − （2-4） ， f' x
f 2 ' = −240mm
8、一短焦距物镜 一短焦距物镜， 焦距物镜，已知其焦距为 35mm，筒长 L=65mm，工作距离 l k ' = 50mm ，按 最简单结构的薄透镜系统考虑， 最简单结构的薄透镜系统考虑，求系统结构。 求系统结构。 解： （仿照 （仿照 P32 P32 例 2） 利用正切计算法，设 h1 = 100mm ，有公式：
1 1 1 d （2-33） = + − f ' f1 ' f 2 ' f1 ' f 2 '
f1 ' f 2 ' nr1 r2 f ' = − f = − ∆ = ( n − 1)[n( r − r ) + ( n − 1)d ] 2 1 1 Φ = f ' − dr2 l ' = H n( r2 − r1 ) + ( n − 1)d − dr1 l = H n( r2 − r1 ) + ( n − 1)d
xx' = ff ' = − f ' 2 ∴ x' = − f2 x
代入数据得：
x = −∞, x' = 0.5625mm x = −10m, x' = 0.703mm x = −6m, x' = 0.9375mm x = −4m, x' = 1.406mm x = −2m, x' = 2.813mm

光学第2章_理想光学系统

光学第2章_理想光学系统

透镜
(6)
空气中的薄透镜焦距
时为正透镜, 正透镜中心比边缘厚, 又称为凸透镜; f ′= f > 0 时为正透镜 正透镜中心比边缘厚 又称为凸透镜 f ′= f <0 时 为负透镜,负透镜中心比边缘薄 又称为凹透镜. 负透镜中心比边缘薄, 为负透镜 负透镜中心比边缘薄 又称为凹透镜
由( 3) 和(5)式, 得空气中的薄透镜成像公式:
按照这种设想,来自无穷远物点和焦点F的两条光线 将既通过Q点亦通过Q'点.Q,Q'是一对共轭点,两个主 平面是一对共轭面,且 β ≡ +1 总之,对于一个光学系统,找到其主平面(一对)和 两个焦点F,F',其系统的基本结构模型就构成了,它们 完全可以代表光学系统的成像性质.
第二节
理想光学系统的基点和基面
Q Q'
.
F
H
H'
.
f'
F'
-f
第二节
理想光学系统的基点和基面
自物方焦点入射的光线与其出射平行于光轴的光线的延长线的交 点Q的垂点H称为主点,相应的垂直于光轴的平面称为物方主平面. 类似地,H'为像方主点,相应垂直于光轴的平面为像方主平面.
Q Q'
.
F
H
H'
.
f'
F'
-f
注意:图中,Q,Q'点并非实际光线的交点,而是实际光线延 长线的交点.引入主平面的概念后,可大大简化成像过程的计算 .不妨就"认为"Q,Q'是实际光线的交点.
y' f l' β = = y f'l
f '= -f
l' β = l

工程光学习题1

工程光学习题1

(n 1)
习题1-8 如图1-6所示，光线芯的折射率为n1，包层的折射 率为n2，光纤所在介质的折射率为n0，求光纤的 数值孔径。
n2 sin I m n1 n0 sin I1 n1 cos I m n n
2 1 2 2
习题1-9 有一直角棱镜如图1-16所示，其折射率为n。问 光线以多大的孔径角入射时，正好能够经其斜面 全反射后出射。如果棱镜用冕牌玻璃K9制造， 计算该孔径角的值。
• 2.已知真空中的光速，求光在水（n=1.333 ）、冕牌玻璃（n=1.51）、火石玻璃（ n=1.65）、加拿大树胶（n=1.526）、金刚 石（n=2.417）等介质中的光速。 c 3 10 c v n • 答：根据 v ，分别代入数字得： n n m / s 3 10 v • （1）在水中（注意单位） 1.333 2.2510 m / s • （2）在冕牌玻璃中 • （3）在火石玻璃中 • （4）在加拿大树胶中 • （5）在金刚石中
L d lF
300m m d L lF f 3 lF
h1 f tanu h1 2 h2 tanu h2 2 lF h1 tanu1 f1 h h d tanu 1 1 2
1 1 2 l l r (1) 0, l l l , l 50m m

无限远轴上物点的共轭 像点正好位于 r / 2处； (2) 0.1, l 550mm, l 55m m； (3) 0.2, l 300mm, l 60m m；
(1) l 时， 0； (2) l 1000mm时， 0.429 ； (3) l 100mm时， 1.5； (4) l 0时，l 0， 物和像都位于折射球面 的顶点， 0； (5) l 100mm时， 0.75； (6) l 150mm时， 0.667 ； (7) l 200mm时， 0.6；

工程光学Chp2习题答案

工程光学Chp2习题答案

A
2
(i ) l = +∞
A' F' H' H F
2．已知照相物镜的焦距 f ' = 75mm ，被摄景物位于（以 F 点为坐标原点） x = −∞ 、－10m、 －8m、 －6m、 －4m、 －2m 处， 试求照相底片应分别放在离物镜的像方焦面多远的地方。 【提示】应用牛顿公式 【解】牛顿公式
xx' = ff '
l1' 1 =− 2 l1
β2 =
− l1 = −l 2 + 100 1 1 1 1 − = ' − l2 l1' l1 l 2
由高斯公式： 解得： f
'
=
− l2 = 100mm 2
7．希望得到一个对无限远成像的长焦距物镜，焦距 f ' = 1200mm ,由物镜顶点到像面的距 离（筒长） L = 700mm ，由系统最后一面到像平面距离（工作距）为 lk = 400mm ，按
则 ϕ1 =
1 40
'
ϕ=
7 1 ϕ2 = 240 240
f 2' = 240mm
可得到 f1 = 40mm
6．有一正薄透镜对某一物成倒立的实像，像高 为物高的一半， 今将物面向物体移近 100mm， 则所得像与物同大小， 求该正透镜组的焦距。 【提示】
5
β1 =
【解】由已知得：
' l2 = −1 l2
H' (A') F'
A F A' H
F' H'
(g) l = f = − f '
(h) l = 2 f = −2 f '

工程光学习题解答

工程光学习题解答

36.2( mm), l F
第二章 理想光学系统
17、有三个薄透镜，其焦距分别为 f1 100mm, f 2 50mm, f 3 50mm, 其间隔 d1 10mm, d 2 10mm 求组合系统的 基点。 h h1 100mm, tan U 2 tan U1 2 解：物方参数 f

lH f
l F l H f 1560mm, l F l H f 1360mm
第二章 理想光学系统
10、解：
f f1f 2

100mm,
f1f 2 f
50mm
d f1 f 2 100mm lH f lH f d f2 d f1 100mm, l F l H f 0
A
OB 50 OB OB 30mm
A
A
n 6、解：0 sin I1 n1 sin I 2 I 2 90 I m
0
n1 sin I m n2 sin 90 sin I m n2 n1 n2 n1
2 2
0
cos I m 1
n0 sin I1 n1 1
H
lH
F2
F1
F
d
l F (lk )
L
f
第二章 理想光学系统
9、已知一透镜 r1 200mm, r2 300mm, d 50mm, n 1.5 ， 求其焦距、光焦度、基点位置。 nr1r2 解： f 1440mm 1.44m
( n 1)[ n( r2 r1 ) ( n 1)] 1 f 0.69 D n 1 n d1 120mm, l H f n 1 n d 2 80mm

工程光学Chp2习题答案

工程光学Chp2习题答案

∴ f1' = −35mm ∴ f 2' = 25mm
9．已知一透镜 r1 = −200mm, r2 = −300mm, d = 50mm, n = 1.5 ，求其焦距,光焦度，基点位置。 【提示】 【解】
ϕ = 1 / f ' = (n − 1)( ρ1 − ρ 2 ) +
f ' = −1440mm
(a ) l = −∞
(b ) l = −2 f
=2f
'
F
H
H'
F'
F
H
H' A'
F'
A
(c ) l = − f
= f
'
(d ) l = − f / 2 =
f '/ 2
F'(A) F H H' A' F H H' A A'
F'
(e ) l = 0
(f ) l =
f / 2 = − f '/ 2
F H(A)
⎧ l1' = = −3 β ⎪ 1 l1 ⎪ ' ⎪ l2 ⎪ β 2 = = −4 l2 ⎪ ⎨− l1 = −l 2 + 18 ⎪ 1 1 1 − = ⎪ ⎪ l '1 l1 f ' ⎪ 1 1 1 ⎪ l' − l = f ' 2 ⎩ 2
⎧ l1 = −288mm ⎪ ⎪ l1 ' = 864mm ⎪ 解得： ⎨l 2 = −270mm ⎪ l ' = 1080mm ⎪2 ⎪ ⎩ f ' = 216mm
h d h2 = h1 − d ⋅ tgu = h1 − d ⋅ 1' = h1 (1 − ' ) f1 f1

理想光学系统习题

理想光学系统习题

第二章 理想光学系统一：选择题（可以有多选)1.有一个无限远物点，经某一理想光学系统成像，陈述正确的是（B ）A.其像点必在理想光学系统的像方焦点处。

B.其像点必在理想光学系统的像方焦平面上。

C.该物点与像点无穷远点共轭。

D.该物点与其像点可作为此理想光学系统的一对基点。

2.有一个置于空气中的理想光学系统，其垂轴放大率β>0,则（ AB ）A.物像位于系统的同侧。

B.角放大率γ>0。

C.像高大于物高。

D.光学系统的焦距为正。

3.一物体经理想光学系统后放大的实像。

当物体向光学系统方向移动一微小距离，则（ AC ）A.其像变大。

B.垂轴放大率β的绝对值变小。

C.角放大率γ的绝对值变小。

D.轴放大率α的绝对值变小。

4.理想光学系统的角放大率γ（ABD ）A.反映了理想光学系统能够把光束变宽或变窄的能力。

B.角放大率γ的大小取决于物像共轭位置。

C.改变理想光学系统物像方折射率的大小，角放大率γ值不变。

D.垂轴放大率β值越大，角放大率γ越小。

二、填空题1、一双凸透镜两球面的曲率半径都是12cm ，透镜玻璃的折射率为1.5，若将此透镜置于空气中，求透镜的焦距__12_ cm ______。

2、共轴理想光学系统的牛顿公式___ xx ’=ff ’______，高斯公式_1''=+lf l f ________。

3、一个折射率为1.52的双凸薄透镜，其中一个折射面的曲率半径是另一个折射面的2倍，且其焦距为5cm ，则这两个折射面的曲率半径分别为_ 7.8 _____cm 和__-3.9____cm 。

4、长60mm ，折射率为1.5的玻璃棒，在其两端磨成曲率半径为10mm 的凸球面，其焦距为____∞简答题1、共轴光学系统的成像性质有哪些？画出一对共轭面及两对共轭点已知情况下的物点和像点。

1、性质1 位于光轴上的物点对应的共轭像点也必然位于光轴上；位于过光轴的某一个截面内的物点对应的共轭像点必位于该平面的共轭像面内；同时，过光轴的任意截面成像性质都是相同的。

工程光学基础2

工程光学基础2

符合点对应点，直线对应直线，平面对应平面的像 称为理想像
能够成理想像的光学系统称为理想光学系统
符合点对应点，直线对应直线，平面对应平面的成 像变换称为共线成像
共轴理想光学系统的成像性质
1.轴上点成像在轴上 A.
.A1’ .A2’
2.位在过光轴的某一截面内的物点对应的像点位在同一平 面内
3.过光轴任一截面内的成像性质是相同的 空间的问题简化为平面问题，系统可用过光轴的一个
反射球面焦距公式 球面反射的情形
反射看作是 n'n 的折射
f ' f r 2
结论:反射球面的焦点位于球心和顶点的中点
共轴球面系统的主平面和焦点
焦点位置： 平行于光轴入射的光线，通过光学系统后，与光轴的交 点就是像方焦点F’
焦点位置计算
把平行于光轴入射的近轴光线逐面计算，最后求得
出射光线的坐标
截面来代表
4.当物平面垂直于光轴时，像平面也垂直于光轴
5. 当物平面垂直于光轴时，像与物完全相似 像和物的比值叫放大率 所谓相似，就是物平面上无论什么部位成像，都是按同 一放大率成像。即放大率是一个常数
y' y
AB OP GH PQ A' B' O' P' G' H' P'Q'
ABOPGH常数 PQ
抛物面：到一条直线和一个定点的距离相等的点的轨迹， 是以该点为焦点，该直线为准线的抛物面。 对焦点和 无限远轴上点符合等光程。
等光程的折射面 二次曲面
两镜系统基本结构形式
常用两镜系统
1、 经典卡塞格林系统
主镜为凹的抛物面，副镜为凸的双曲面，抛物面的 焦点和双曲面的的虚焦点重合，经双曲面后成像在其 实焦点处。卡塞格林系统的长度较短，主镜和副镜的 场曲符号相反，有利于扩大视场。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

工程光学习题解答--第二章-理想光学系统
第二章 理想光学系统
1.针对位于空气中的正透镜组()0
'
>f
及负透镜组
()0
'
<f
，试用作图法分别对以下物距
∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。

解：1.0'
>f ()-∞=l a
()'
l b
()'
f f l c
=-=
()
d
()l e ()2/'2/f
f l f -==
')(f f l g -==
l
h-
=
=
'
f
2 (f
2
)
+∞
l i)(
= Array
2.0'<f
c(
(
l g )(
+∞
=l i )(
2. 已知照相物镜的焦距f’＝75mm,被摄景物位于（以F点为坐标原点）=x,2,4,6,8,
-
-
∝
-处，
-
-
m
10
,m
m
m
m-
试求照相底片应分别放在离物镜的像方焦面多
远的地方。

解：（1）x= -∝，xx′=ff′得到：x′=0
（2）x′=0.5625
（3）x′=0.703
（4）x′=0.937
（5）x′=1.4
（6）x′=2.81
3.设一系统位于空气中，垂轴放大率*
β，由
=10
-
物面到像面的距离（共轭距离）为7200mm，物镜两焦点间距离为1140mm。

求该物镜焦距，
并绘出基点位置图。

解:
∵ 系统位于空气中，f
f
-='
10'
'-===
l
l y y β
由已知条件：1140)('
=+-+x f f
7200)('
=+-+x l l
解得：mm
f
600'
= mm x 60-=
4.已知一个透镜把物体放大*-3投影到屏幕上，当透镜向物体移近18mm 时，物体将被放大*-4，试求透镜的焦距，并用图解法校核之。

解：方法一：
3
1
'
11-==l l β
⇒
()
183321'1--=-=l l l ①
4
2
'2
2-==l l β ⇒ 2
'2
4l l -=
②
18
21+-=-l l ⇒ 18
21
-=l l
③
'
/1/1/11'1f l l =- '
/1/1/12'2f l l =- 将①②③代入④中得 mm
l
2702
-= mm
l
1080'2
-=
∴ mm f 216'=
方法二： 31
1
-=-
=x f
β
42
2
-=-
=x f
β
⇒
mm
f 216-=
18
12
=-x x
方法三： 12
)4)(3(21''=--==∆∆=ββαn
n x x
2161812'
-=⨯=∆x
'
'
f
x -=βΘ
143''
'
'2
'121
=+-=∆=+-=
-∴f
x f
x x ββ
mm
x f
216''
=∆=∴
5.一个薄透镜对某一物体成实像，放大率为⨯
-1,今以另一个薄透镜紧贴在第一个透镜上，则见像向透镜方向移动，放大率为原先的3/4倍，求两块透镜的焦距为多少？ 解：
⇒ 2
'2
1
'
1
/1/1/1/1l l l l -=- ④
6.有一正薄透镜对某一物成倒立的实像，像高为物高的一半，今将物面向物体移近100mm ， 则所得像与物同大小，求该正透镜组的焦距。

解：由已知得：
2
1
1'11-
==l l β
1
2
'2
2-==l l β 100
21
+-=-l l
由高斯公式：2
'2
1
'1
1111l l l l -=-
解得：mm l
f 10022
'=-=
7.希望得到一个对无限远成像的长焦距物镜，焦距mm
f
1200'
=，由物镜顶点到像面的距离L=mm 700，
由系统最后一面到像平面的距离（工作距）为
，按最简单结构的薄透镜系统考虑，求系
统结构，并画出光路图。

解：
-
l '
1
100-l 2
l '2
8. 一短焦距物镜，已知其焦距为mm 35，筒长L=mm 65，工作距mm
l
k
50'=,按最简单结构的薄透镜系
统考虑，求系统结构。

解：
9.已知一透镜5
.1,50,300,2002
1
==-=-=n mm d mm r
mm r ，求其焦
距,光焦度，基点位置。

解：已知5
.1,50,300,2002
1
==-=-=n mm d mm r
mm r 求：,'
f ϕ,基点位置。

1
2
1
2
2
1
69.0)
1())(1('/1--=-+--==m d n
n n f ρ
ρρρϕ
mm
f 1440'
-=
mm d n n f l F
1560)1
1('1'-=--
=ρ mm
d n n f l F 1360)1
1('2=-+-=ρ
mm
d n n f l H 120)1('1'
-=--=ρ
mm d n
n f l
H
80)1
(
'2-=-=ρ
10. 一薄透镜组焦距为mm 100，和另一焦距为mm 50的薄透镜组合，其组合焦距仍为mm 100，问两薄透镜的相对位置，并求基点位置，以图解法校核之。

解：
11. 长mm 60，折射率为1.5的玻璃棒，在其两端磨成曲率半径为mm 10的凸球面，试求其焦距及基点位置。

解：
12. 一束平行光垂直入射到平凸透镜上，会聚于透镜后mm
480处，如在此透镜凸面上镀银，则平
行光会聚于透镜前mm
80处，求透镜折射率和凸面曲率半径。

解：
13.一块厚透镜，,
30,320,120,6.12
1
mm d mm r
mm r n =-===试求该
透镜焦距和基点位置。

如果物距m
l
51
-=时，问像
在何处？如果平行光入射时，使透镜绕一和光轴垂直的轴转动，而要求像点位置不变，问该轴应装在何处？ 解：
⑴[]
mm d n r r n n r
nr f 27.149)1()()1('12
21=-+--= mm d n n f l F 28.135)1
1(1''
=--
=ρ
mm
d n n f l F 02.144)1
1(2'-=-+-=ρ
mm
d n n f l H 99.1311''
-=--=ρ
mm
d n
n f l H 25.51
2'=--=ρ
⑵mm
l l
l H 25.500525.550001
-=--=-=
'
'
1
11f
l l =
-Θ mm
l 86.153'
=∴
mm l l l H
89.13999.1386.153'''2=-=+=
⑶绕过像方节点位置轴旋转，'
H 点处。

14 思考题：
1、同一物体经针孔或平面镜所成的像有何不同？
答：由反射定律可知，平面镜的物和像是关于镜面对称的。

坐标由右旋坐标
系变为像的左旋坐标系，因此像和物左右互易上下并不颠倒。

即物体经平面镜生 成等大、正立的虚像。

物体经针孔成像时，物点和像点之间相对于针孔对称。

右旋坐标系惊针孔所
成的像仍为右旋坐标系，因此像和物上下左右都是互易的，而且像的大小与针孔
到接收屏的距离有关。

即物体经针孔生成倒立的实像。

2、一束在空气中波长为589.3nm 的钠黄光，从
空气进入水中时，它的波长将变
为多少？在水中观察这束光时，其颜色会改变吗？
3、凹透镜可否单独用作放大镜？
答：因凹透镜对实物只能生成缩小的虚像，当人眼通过凹透镜观察物体时，
人眼对缩小的虚像的视角总是小于（最多等于）不用凹透镜时直接观察物体的视
角（这是人眼须紧贴凹透镜），故凹透镜的视角放大率不可能大于1。

所以凹透
镜不能单独用作放大镜。

4、薄透镜的焦距与它所在介质是否有关？凸透镜一定是会聚透镜吗？凹透镜一
定是发散透镜吗？。