中国邮递员问题的应用

基于中国邮递员问题的物流配送线路优化[摘要]：针对物流配送的线路优化问题，以配送总路程最小为目标，在充分考虑中国邮递员问题的基础上，寻求求解优化方案以及建立线路优化模型。

[关键词]：线路优化中国邮递员问题最小树法优化模型1.引言随着市场竞争的日益加剧、世界经济一体化的程度的加快和科学技术的飞速发展，许多企业已经把物流作为提高竞争力和提升核心的竞争能力的重要手段，将先进的物流理论和物流技术引入企业的生产和经营管理中。

这一产业在我国现今还处于发展阶段，与国外物流业相比，我国物流业自身存在的一些问题逐渐对企业自身的发展和盈利造成了瓶颈。

在众多的问题中，物流效率问题是较为突出的一个。

而物流网络是否科学健全又是决定物流效率的关键一环，作为实现物流合理化的重要内容和手段，研究物流配送路径有助于企业降低物流成本，提高运作效率，全面提高顾客满意度，使企业在现今物流业服务竞争逐渐激烈的环境下站稳脚跟，让企业获得更多的利润和更为长远的发展。

用图的语言来描述物流线路优化问题，就是给定一个连通图G，在每条边上有一个非负的权，要寻求一个圈，经过G的每条边至少一次，并且圈的权数最小。

这个问题是由我国管梅谷同志于1962年首先提出来的，因此国际上称它为中国邮递员问题。

2.问题描述中国邮递员问题的描述：一个邮递员送信，在邮局里挑选出他所有负责的街区的各条街道的邮件，并按一定的次序排列，然后按一定路线投递这些邮件，最后返回邮局。

自然邮递员必须走过他负责的街区的每一条街道至少一次，并希望选择一条总路程最短的投递路线。

下面我们介绍一下图论问题中的定义和定理。

定义1：在一个多重边的连通图中，从某个顶点出发，经过不同的线路，又回到原出发点，这样的线路称为欧拉图。

定义2：设G是一个无向连通图，若存在一个回路，经过G中的每一条边一次且仅一次，则称这个同路为欧拉回路：定义3：设G足一个无向连通图，若在G中通过某顶点的弧的个数为偶数时，这个顶点被称为偶点，否则被称为奇点。

中国邮递员问题摘要：一名邮递员带着要分发的邮件从邮局出发，经过要分发的每个街道，送完邮件后又返回邮局．如果他必须至少一次走过他管辖范围内的每一条街道，如何选择投递路线，使邮递员走尽可能少的路程．这个问题是由我国数学家管梅谷先生（山东师范大学数学系教授）在1962年首次提出的，因此在国际上称之为中国邮递员问题本文主要介绍了中国邮递员问题的基本分析、求解中国邮递员问题的方法以及有关欧拉回路的算法实现。

关键词：中国邮递员欧拉图欧拉回路一、中国邮递员问题的分析中国投递员问题是1960年我们从生产实际中提出的一个数学问题，它是从下述实际问题中抽象出来的：“一个投递员应该怎么选择一条线路，才能既把所有由他负责的信件都送到，而所走的路程又最短”。

在我们开始研究中国投递员问题以前，国外有人研究过所谓旅行售货员的问题，即：“一个售货员要到n个城市去售货，问他应该选择怎样的一条线路，才能既走遍所有城市，并且走的路程最短”。

这是一个著名的难题.当n较大时，即使使用大型电子计算机，也很难解决。

投递员面临的问题显然可以归纳为旅行售货员问题，事实上，只要把投递员必须送的每一个地点看成是一个城市就行了.但是一般来说，投递员每次要到约二、三百个地点送信，如果归纳为旅行售货员问题来解决，将是一个规模很大的问题，是无法解决的.但是，在仔细分析了投递员面临的问题后，我们发现这个问题具有一定的特点，即需要送信的地点一般都是比较密集的排列在街道上的，因此，实际上，我们称这个问题为“最短投递线路问题”，1965年后国外称之为“中国投递员问题”(这个问题是我国数学家管梅谷先生在20世纪60年代提出来的)用图论的语言来描述就是在一个带权图G中，能否找到一条回路C，使C包含G的每条边至少一次且C的长度最短？如若他所管辖的街道构成一欧拉回路，则这欧拉回路便是所求路径。

如若不然，即存在度数为奇数的顶点，必然有些街道需要多走至少一遍，这时用中国邮路问题算法可求出最短路径。

邮差问题算法【实用版】目录1.邮差问题的定义与背景2.邮差问题的数学模型3.邮差问题的算法解决方案4.邮差问题算法的应用案例5.总结正文1.邮差问题的定义与背景邮差问题，又称为邮递员问题，是图论中的基本问题之一。

这个问题可以追溯到 1960 年，当时我国数学家管梅谷首次对其进行了研究。

邮差问题的背景是这样的：假设有一个邮递员从邮局出发，他需要将信件送到辖区内的每条街道，并且每条街道至少要经过一次，最后再返回邮局。

那么，在这个条件下，如何选择一条最短的路线呢？这个问题就是邮差问题。

2.邮差问题的数学模型为了更好地理解邮差问题，我们可以将其抽象为一个图论模型。

在这个模型中，邮局作为图的一个顶点，每条街道作为图的一条边，而邮递员需要经过的街道就是图中的路径。

目标是找到一条从邮局出发，经过所有街道一次后返回邮局的最短路径。

3.邮差问题的算法解决方案针对邮差问题，有多种算法可以求解。

这里我们介绍两种常用的算法：欧拉回路算法和 Hamilton 回路算法。

欧拉回路算法：欧拉回路是指在一个图中，经过每条边一次且回到起点的路径。

欧拉回路算法可以解决邮差问题，其基本思想是：从任意一个顶点出发，尝试遍历所有顶点，如果遇到已经访问过的顶点，则尝试回溯，直至找到一条欧拉回路。

Hamilton 回路算法：Hamilton 回路是指在一个图中，经过每条边恰好一次且回到起点的路径。

与欧拉回路算法类似，Hamilton 回路算法也是从任意一个顶点出发，尝试遍历所有顶点。

不同之处在于，当遇到已经访问过的顶点时，算法会尝试通过一个尚未访问的顶点回到起点，以形成一个 Hamilton 回路。

4.邮差问题算法的应用案例邮差问题算法在实际生活中有很多应用，例如物流配送、DNA 测序、无线通信等。

以物流配送为例，假设有一个物流公司需要在若干个仓库之间运送货物，每个仓库至少要经过一次，那么如何规划路线才能使得总路程最短呢？这时，邮差问题算法就可以派上用场。

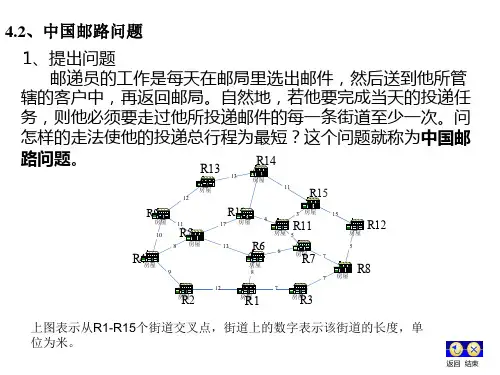
§4.中国邮递员问题（Chinese Postman Problem）1．问题的提出例5. 一个邮递员从邮局出发投递信件, 然后再返回邮局, 如果他必须至少一次地走过他负责投递范围内的每条街道, 街道路线如下图所示, 问选择怎样的路线才能使所走的路为最短?5 6 78问题的图论表述：在赋权G=[V, E]上找一条经每条边至少一次的权最小的圈。

1960年山东师范学院管梅谷教授首先提出此问题，并设计了一个“奇偶点表上作业法”，后来发现此法不是多项式算法，1973年，Edmonds和Johnson给出一个多项式算法。

2．哥尼斯堡七桥问题18世纪在哥尼斯堡城(今俄罗斯加里宁格勒)的普莱格尔河上有7座桥，将河中的两个岛和河岸连结，如下图所示。

城中的居民经常沿河过桥散步，于是提出了一个问题：能否一次走遍7座桥，而每座桥只许通过一次，最后仍回到起始地点。

3．Euler圈Euler圈：经图G的每条边的简单圈Euler图：具有Euler圈的图Euler图非Euler图下面讨论的图G允许有重边，且重边被认为是有区别的边。

伪Euler 圈：经图G 的每条边至少一次的圈点v 的次：与点V 关联的边的数目奇(偶)点：该点的次为奇(偶)数命题1：G 的奇点个数为偶数命题2：G 中有伪Euler 圈 ⇔ G 无奇点中国邮递员问题可表述为：在图G 中找一条权最小的伪Euler 圈。

对于邮递员来说，有些街道可能会重复走，原问题便转化为尽可能少走重复的 街道。

我们将这些重复的边组成的集合称可行集，即找最小的可行集。

命题3：E *是最小可行集 ⇔ωωμμμ()()()()*()*()e e e E E E e E E ≤∑∑∀μ∈∩∈∩\初等圈重复的边 非重复的边4．算法思路由命题1，简单图G 的奇点个数为偶数，可设为v 1 , v 2 , …, v 2k , 对每个1≤ i ≤k, 找v 2i − 1 至v 2i 的链p i ，将p i 的边重复一次。

中国邮递员问题摘要：一名邮递员带着要分发的邮件从邮局出发，经过要分发的每个街道，送完邮件后又返回邮局．如果他必须至少一次走过他管辖范围内的每一条街道，如何选择投递路线，使邮递员走尽可能少的路程．这个问题是由我国数学家管梅谷先生（山东师范大学数学系教授）在1962年首次提出的，因此在国际上称之为中国邮递员问题本文主要介绍了中国邮递员问题的基本分析、求解中国邮递员问题的方法以及有关欧拉回路的算法实现。

关键词：中国邮递员欧拉图欧拉回路一、中国邮递员问题的分析中国投递员问题是1960年我们从生产实际中提出的一个数学问题，它是从下述实际问题中抽象出来的：“一个投递员应该怎么选择一条线路，才能既把所有由他负责的信件都送到，而所走的路程又最短”。

在我们开始研究中国投递员问题以前，国外有人研究过所谓旅行售货员的问题，即：“一个售货员要到n个城市去售货，问他应该选择怎样的一条线路，才能既走遍所有城市，并且走的路程最短”。

这是一个著名的难题.当n较大时，即使使用大型电子计算机，也很难解决。

投递员面临的问题显然可以归纳为旅行售货员问题，事实上，只要把投递员必须送的每一个地点看成是一个城市就行了.但是一般来说，投递员每次要到约二、三百个地点送信，如果归纳为旅行售货员问题来解决，将是一个规模很大的问题，是无法解决的.但是，在仔细分析了投递员面临的问题后，我们发现这个问题具有一定的特点，即需要送信的地点一般都是比较密集的排列在街道上的，因此，实际上，我们称这个问题为“最短投递线路问题”，1965年后国外称之为“中国投递员问题”(这个问题是我国数学家管梅谷先生在20世纪60年代提出来的)用图论的语言来描述就是在一个带权图G中，能否找到一条回路C，使C包含G的每条边至少一次且C的长度最短？如若他所管辖的街道构成一欧拉回路，则这欧拉回路便是所求路径。

如若不然，即存在度数为奇数的顶点，必然有些街道需要多走至少一遍，这时用中国邮路问题算法可求出最短路径。