理论力学第二章(力系的等效与简化)

第二章 力系的简化 习题解答2-1在立方体的顶点A 、H 、B 、D 上分别作用四个力，大小均为F ，其中1F 沿AC ，2F 沿IG ，3F 沿BE ，4F 沿DH 。

试将此力系简化成最简形式。

解：各力均在与坐标平面平行的面内，且与所在平面的棱边成45°角。

将力系向A 点简化，主矢'R F 在坐标轴上的投影为045cos 45cos '21=-=F F F Rx ，FF F F F F Ry 245cos 45cos 45cos 45cos '4321=+-+=，F F F F Rz 245cos 45cos '43=+= 。

用解析式表示为： ()k j F +=F R 2'设立方体的边长为a ，主矩A M 在坐标轴上的投影为 045cos 45cos 32=⋅+⋅-=a F a F M Ax ， Fa a F a F M Ay 245cos 45cos 42-=⋅-⋅-= ，Fa a F a F M Az 245cos 45cos 42=⋅+⋅= 。

用解析式表示为：()k j M +-=Fa A 2。

因为，0'=⋅A R M F ，所以，主矢和主矩可以进一步简化为一个力，即力系的合力。

合力的大小和方向与主矢相同，'R R F F =；合力作用点的矢径为()i MF r a F R R =⨯=2''，所以，合力大小为2F ，方向沿对角线DH 。

2-2三力321,F F ,F 分别在三个坐标平面内，并分别与三坐标轴平行，但指向可正可负。

距离c b a ,,为已知。

问：这三个力的大小满足什么关系时力系能简化为合力？又满足什么关系时能简化为力螺旋？解：这力系的主矢为k j i 321'F F F F R ++=； 对O 点的主矩为k j i a F c F b F M O 213++=。

当主矢与主矩垂直时，力系能简化为合力。

第2章 力系的等效与简化2－1试求图示中力F 对O 点的矩。

解：（a ）l F F M F M F M M y O y O x O O ⋅==+=αsin )()()()(F （b ）l F M O ⋅=αsin )(F（c ）)(sin cos )()()(312l l Fl F F M F M M y O x O O +--=+=ααF （d ）2221sin )()()()(l l F F M F M F M M y O y O x O O +==+=αF2－2 图示正方体的边长a =0.5m ，其上作用的力F =100N ，求力F 对O 点的矩及对x 轴的力矩。

解：)(2)()(j i k i Fr F M +-⨯+=⨯=Fa A O m kN )(36.35)(2⋅+--=+--=k j i k j i Fam kN 36.35)(⋅-=F x M2－3 曲拐手柄如图所示，已知作用于手柄上的力F =100N ，AB =100mm ，BC =400mm ，CD =200mm ，α = 30°。

试求力F 对x 、y 、z 轴之矩。

解：)cos cos sin (sin )4.03.0()(2k j i k j F r F M αααα--⨯-=⨯=F D Ak j i αααα22sin 30sin 40)sin 4.03.0(cos 100--+-=力F 对x 、y 、z 轴之矩为：m N 3.43)2.03.0(350)sin 4.03.0(cos 100)(⋅-=+-=+-=ααF x M m N 10sin 40)(2⋅-=-=αF y Mm N 5.7sin 30)(2⋅-=-=αF z M2—4 正三棱柱的底面为等腰三角形，已知OA=OB =a ，在平面ABED 内沿对角线AE 有一个力F ， 图中θ =30°，试求此力对各坐标轴之矩。

习题2-1图A r A习题2-2图（a ）习题2-3图(a)ABr 解：)sin 45sin cos 45cos cos ()(k j i i F r F M θθθ+︒+︒-⨯=⨯=F a A O )45sin cos sin (k j ︒+-=θθaF 力F 对x 、y 、z 轴之矩为：0)(=F x M230sin )(aF aF M y -=︒-==F Fa aF M z 4645sin 30cos )(=︒︒=F2－5 如图所示，试求力F 对A 点之矩及对x 、y 、z 轴之矩。

第二章力系的简化习题解[习题2-1] 一钢结构节点,在沿OA,OB,OC的方向上受到三个力的作用,已知,,,试求这三个力的合力.解:作用点在O点,方向水平向右.[习题2-2] 计算图中已知,,三个力分别在轴上的投影并求合力. 已知,,.解:合力的大小:方向余弦:作用点:在三力的汇交点A.[习题2-3] 已知,,,,求五个力合成的结果(提示:不必开根号,可使计算简化).解:合力的大小: 方向余弦:作用点:在三力的汇交点A.[习题2-4] 沿正六面体的三棱边作用着三个力,在平面OABC内作用一个力偶. 已知,,,.求力偶与三个力合成的结果.解:把,,向平移,得到:主矢量:的方向由E指向D.主矩:方向余弦:[习题2-5] 一矩形体上作用着三个力偶,,.已知,,,,求三个力偶合成的结果.解:先把在正X面上平行移动到x轴.则应附加力偶矩:把沿轴上分解:主矩:方向余弦:[习题2-6] 试求图诸力合成的结果.解:主矢量:竖向力产生的矩顶面底面斜面-0.76 0.2 0.75 主矩:方向余弦:[习题2-7] 柱子上作有着,,三个铅直力, 已知,,,三力位置如图所示.图中长度单位为,求将该力系向点简化的结果.解:主矢量:竖向力产生的矩3.5 1.7 0主矩:方向余弦:[习题2-8] 求图示平行力系合成的结果(小方格边长为)解:主矢量:ABCD8.4 -4.35主矩:方向余弦:[习题2-9] 平板OABD上作用空间平行力系如图所示,问应等于多少才能使该力系合力作用线通过板中心C.解:主矢量:由合力矩定理可列出如下方程:[习题2-10] 一力系由四个力组成。

已知F1＝60Ｎ，F2＝400Ｎ，F3＝500Ｎ，F4＝200Ｎ，试将该力系向Ａ点简化(图中长度单位为mm)。

解:主矢量计算表0 0 600 200 0300 546.41 -140方向余弦:-110.564 120 0 主矩大小:方向余弦:[习题2-11]一力系由三力组成，各力大小、作用线位置和方向见图。

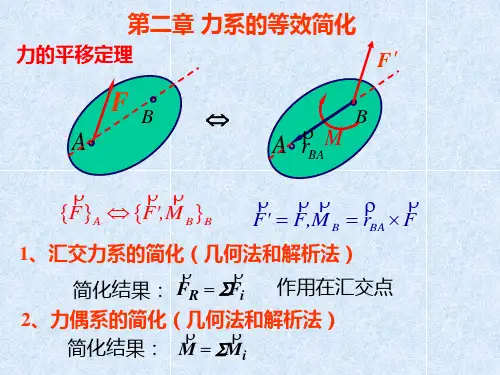
第二章力系简化理论◆力的平移定理◆力系的主矢和主矩◆力系向一点简化◆力系简化结果分析§2–2 主矢和主矩·力系向一点的简化∑∑⨯==ii i O O F r )F (M M R i ix iy ix F F F i F j F k'==++∑∑∑∑ 称为该力系对O 点的主矩（principal moment ）称为该力系的主矢（principal vector ）式中， 分别表示各力对x ，y ，z 轴的矩。

(),(),()x y z M F M F M F空间任意力系的n 个力的矢量和1. 力系的主矢、主矩取任意点O ， n 个力对O 点之矩的矢量和kF M j F M i F M M i z i y i x O ∑∑∑++=)()()(由F 1、F 2组成的空间力系，已知：F 1 = F 2 = F 。

试求力系的主矢F R 以及力系对O 、A 、E 三点的主矩。

1. 计算力系主矢令i 、j 、k 为x 、y 、z 方向的单位矢量，则力系中的二力可写成力系的主矢为：)43(51j i F +=F)43(52j i F -=FiF F F F F i i R 562121=+==∑= 例：求主矢、主矩解：解： 2. 计算主矩应用矢量叉乘方法，力系对O 、A 、E 三点的主矩分别为：()2211M M F r F O O i i i i i ====⨯∑∑2211F r F r ⨯+⨯=)43(53j i k +⨯=F )43(54j i j -⨯+F)12912(5k j i -+-=F)43(51j i F +=F)43(52j i F -=F∑=⨯+⨯=⨯=2121i EC EA i i E F r F r F r M )12912(5k j i ---=F)12912(k j i +--=F)43(5)34(j i k j -⨯-=F )43(53)43(54j i k j i j -⨯-+⨯-=FF 2210F r F r M ⨯+=⨯=∑=AC i i i A 对O 点对A 三点对E 点其中，各 ，各i iF F '= ()i o i M M F =该汇交力系与力偶系与原任意力系等效。

理论力学常见问题及解答第2单元：力系的简化1. 任意力系亦可由力平行四边形法则（或力多边形法则）得到简化结果吗？ 解答：不能。

因为平行四边形法则（或力多边形法则）只能应用于汇交力系。

参考资料：贾启芬，刘习军. 《理论力学》，机械工业出版社2011第2版萧龙翔等.《理论力学》，天津大学出版社1995关键词：任意力系，力的平行四边形法则，力的多边形法则，汇交力系2. 如何应用力的平移定理解释偏心力对立柱的作用效果？解答：将力平移到立柱的轴线上，得到一个力和一个附加力偶，该力使立柱产生受压变形，而该力偶使立柱产生弯曲变形。

参考资料：贾启芬，刘习军. 《理论力学》，机械工业出版社2011第2版萧龙翔等.《理论力学》，天津大学出版社1995范钦珊. 《理论力学》，清华大学出版社2004(美)施皮格尔（M.R.Spiegel ）. 《理论力学 • 理论和习题》，科学出版社1983关键词：力的平移定理，立柱，作用效果3. 如何理解力系的两个不变量？解答：主矢量'R 和主矢量与主矩的标量积O M R '均与简化中心O 无关，是力系的固有属性，因此称为力系的不变量。

参考资料：贾启芬，刘习军. 《理论力学》，机械工业出版社2011第2版萧龙翔等.《理论力学》，天津大学出版社1995范钦珊. 《理论力学》，清华大学出版社2004洪嘉振，杨长俊. 《理论力学》，高等教育出版社2008（第3版） 关键词：力系的不变量，主矢量，主矩，简化中心4.如何从力系简化，理解固定端约束反力的表达方法？解答：固定端约束的反力是空间分布力系，将该力系向梁与基础连接点简化，得到一个力（主矢量）和一个力偶（主矩），将该力和力偶矩矢量向三个方向正交分解，得到固定端约束反力的表达方式，如图。

参考资料：贾启芬，刘习军. 《理论力学》，机械工业出版社2011第2版萧龙翔等.《理论力学》，天津大学出版社1995范钦珊. 《理论力学》，清华大学出版社2004洪嘉振，杨长俊. 《理论力学》，高等教育出版社2008（第3版）(美)施皮格尔（M.R.Spiegel）. 《理论力学•理论和习题》，科学出版社1983关键词：固定端，反力，力系简化5.当力系第二不变量为零时，共有几种简化结果？解答：共3种：力系平衡，力，力偶。

C(a-2)DR(a-3)(b-1)DR第1篇 工程静力学基础第1章 受力分析概述1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。

试将同一力F 分别对两坐标系进行分解和投影，并比较分力与力的投影。

习题1－1图解：（a ）图（c ）：11 s i n c o s j i F ααF F +=分力：11 cos i F αF x = ， 11 s i n j F αF y =投影：αcos 1F F x = ， αs i n 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。

（b ）图（d ）： 分力：22)cot sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y = 投影：αcos 2F F x = ， )cos(2αϕ-=F F y讨论：ϕ≠90°时，投影与分量的模不等。

1－2 试画出图a 和b习题1－2图比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。

（c ） 22x（d ）1－3 试画出图示各物体的受力图。

习题1－3图B或(a-2)B(a-1)(b-1)F(c-1) 或(b-2)(e-1)F(a)1－4 图a 所示为三角架结构。

荷载F 1作用在铰B 上。

杆AB 不计自重，杆BC 自重为W 。

试画出b 、c 、d 所示的隔离体的受力图，并加以讨论。

习题1－4图1－5 图示刚性构件ABC 由销钉A 和拉杆D 支撑，在构件C 点作用有一水平力F 。

试问如果将力F 沿其作用线移至D 或E （如图示），是否会改为销钉A 的受力状况。

解：由受力图1－5a ，1－5b 和1－5c 分析可知，F 从C 移至E ，A 端受力不变，这是因为力F 在自身刚体ABC 上滑移；而F 从C 移至D，则A 端受力改变，因为HG 与ABC 为不同的刚体。

1(f-1)'A(f-2)1O(f-3)F F'F 1(d-2)F yB 21(c-1)F A B1B FDx y(b-2)1(b-3)F yB 2 A A B1B F习题1－5图AxF(b-3)E D(a-3)B(b-2)(b-1)F 'CBC(c)AxF1－6 试画出图示连续梁中的AC 和CD 梁的受力图。

1F 2F 3F 0135090O第二章 力系的简化习题解[习题2-1] 一钢结构节点,在沿OA,OB,OC 的方向上受到三个力的作用,已知kN F 11=,kN F 41.12=,kN F 23=,试求这三个力的合力.解:01=x F kN F y 11-=)(145cos 41.102kN F x -=-= )(145sin 41.102kN F y ==kN F x 23= 03=y F)(121030kN F F i xi Rx =+-==∑=00113=++-==∑=i yi Ry F F122=+=Ry Rx R R F F 作用点在O 点,方向水平向右.[习题2-2] 计算图中已知1F ,2F ,3F 三个力分别在z y x ,,轴上的投影并求合力. 已知kN F 21=,kN F 12=,kN F 33=.解:kN F x 21= 01=y F 01=z F)(424.0537071.01cos 45sin 022kN F F x =⨯⨯==θ)(567.0547071.01sin 45sin 022kN F F y =⨯⨯==θ)(707.0707.0145sin 022kN F F z =⨯== 03=x F 03=y F kN F z 33= )(424.20424.0230kN F F i xi Rx =++==∑=)(567.00567.0030kN F F i yi Ry =++==∑=)(707.33707.003kN F F i zi Rz =++==∑=合力的大小:)(465.4707.3567.0424.2222222kN F F F F Rz Ry Rx R =++=++=方向余弦:4429.0465.4424.2cos ===R Rx F F α 1270.0465.4567.0cos ===R Ry F F βy8302.0465.4707.3cos ===R Rz F F γ 作用点:在三力的汇交点A.[习题2-3] 已知N F 621=,N F 322=,N F 13=N F 244=,N F 75=,求五个力合成的结果(提示:不必开根号,可使计算简化).解:01=x F 01=y F N F z 621-=02=x F N F y 322= 02=z F N F x 13-= 03=y F 03=z F)(221222460cos 45cos 0044N F F x =⨯⨯==)(3223222460sin 45cos 0044N F F y -=⨯⨯-=-=)(4222445sin 044N F F z =⨯==)(353)62(3457cos sin 22255N F F x =⨯++⨯==θγ)(454)62(3457sin sin 22255N F F y =⨯++⨯==θγ )(62)62(34627cos 22255N F F z =++⨯==γ)(43210050N F F i xi Rx =++-+==∑=)(4432032050N F F i yi Ry =++-++==∑=)(462400625N F F i zi Rz =++++-==∑=合力的大小:)(93.634444222222N F F F F Rz Ry Rx R ==++=++=方向余弦:33344cos ===R Rx F F α33344cos ===RRy F F β 33344cos ===R Rz F F γ "'08445433arccos====γβα 作用点:在三力的汇交点A.[习题2-4] 沿正六面体的三棱边作用着三个力,在平面OABC 内作用一个力偶. 已知N F 201=,N F 302=,N F 503=,m N M ⋅=1.求力偶与三个力合成的结果.解:把1F ,2F ,3F 向1O 平移,得到:主矢量: 0302050213---=--=F F F F R)(42.0202.0)(11m N F F M x ⋅-=⨯-=⨯-= 0)(1=F M y0)(1=F M z)(62.0302.0)(22m N F F M x ⋅-=⨯-=⨯-= )(5.415.03015.0)(22m N F F M y ⋅=⨯=⨯=0)(2=F M z 0)(3=F M x)(5.715.05015.0)(33m N F F M y ⋅-=⨯-=⨯-=0)(3=F M zM 的方向由E 指向D.)(25.825.65.2)()(3111m N F M F M M O O OC ⋅=+=+=∑)(8.01502002001sin 22m N M M x ⋅=+⨯==θ)(6.01502001501cos 22m N M M y ⋅-=+⨯-=-=θA 3F mm图题42-D图题52-xya0=z M)(2.98.0064)(31m N M F M Mx i i x x⋅-=++--=+=∑∑=)(6.36.05.75.40)(31m N M F M M y i i y y⋅-=--+=+=∑∑=00000)(31=+++=+=∑∑=z i i z zM F M M主矩:)(88.90)6.3()2.9()()()(222222m N M M M M z y x O ⋅=+-+-=++=∑∑∑方向余弦:9312.088.92.9cos 0-=-==∑M M xα 3644.088.96.3cos 0-=-==∑M M yβ 088.90cos 0===∑M Mzγ [习题2-5] 一矩形体上作用着三个力偶),('11F F ,),('22F F ,),('33F F .已知N F F 10'11==,N F F 16'22==,N F F 20'33==,m a 1.0=,求三个力偶合成的结果.解:先把1F 在正X 面上平行移动到x 轴. 则应附加力偶矩:)(11.010)(11m N a F F M x ⋅=⨯==)(1)(11m N F M M x x ⋅==)(22.010211m N a F M y ⋅-=⨯-=⋅-=01=z M把2F 沿z y ,轴上分解:)(314.117071.01645cos 022N F F y =⨯==)(314.117071.01645sin 022N F F z =⨯== 02=x M)(263.22.0314.11222m N a F M z y ⋅-=⨯-=⋅-= )(263.22.0314.11222m N a F M y z ⋅=⨯=⋅=03=x M 03=y M)(21.02033m N a F M z ⋅-=⨯-=⋅-=100131=++==∑∑=i xi xM M)(263.40263.2231m N M M i yi y⋅-=+--==∑∑=)(263.02263.2031m N M Mi zi z⋅=-+==∑∑=主矩:)(387.4263.0)263.4(1)()()(222222m N M M M M z y x O ⋅=+-+=++=∑∑∑方向余弦:2280.0387.41cos 0===∑M Mxα 9717.0387.4263.4cos 0=-==∑M M y β 0599.0387.4263.0cos 0===∑M M zγ [习题2-6] 试求图诸力合成的结果. 解: 主矢量:0725=-+=R F)(086.175.02.0)76.0()()()(222222m N M M M M z y x O ⋅=++-=++=∑∑∑方向余弦:6996.0086.176.0cos 0-=-==∑M M xα1842.0086.12.0cos 0===∑M M yβ 6906.0086.175.0cos 0===∑M M zγ[习题2-7] 柱子上作有着1F ,2F ,3F 三个铅直力, 已知kN F 801=,kN F 602=, kN F 503=,三力位置如图所示.图中长度单位为mm ,求将该力系向O 点简化的结果.解:)(190506080kN F -=----= 主矢量: )(891.307.15.3)()()(222222m N M M M M z y x O ⋅=++=++=∑∑∑方向余弦:8995.0891.35.3cos 0===∑M Mxα 4369.0891.37.1cos 0===∑M Myβ 0891.30cos 0===∑M Mzγ [习题2-8] 求图示平行力系合成的结果(小方格边长为mm 100)图习题82-题2—9图解: 0937712=---+=F主矢量:主矩:)(46.9)35.4(4.8)()(2222m kN M M M y x O ⋅=-+=+=∑∑方向余弦:8879.046.94.8cos 0===∑M M xα 4598.046.935.4cos 0=-==∑M M yβ [习题2-9] 平板OABD 上作用空间平行力系如图所示,问y x ,应等于多少才能使该力系合力作用线通过板中心C. 解: 主矢量:)(3046587kN F R -=-----= 由合力矩定理可列出如下方程: 43088854⨯-=⨯-⨯--y12064404=++y )(4m y =33066654⨯=⨯+⨯+x )(6m x =[习题2-10] 一力系由四个力组成。