湖南省普通高等学校

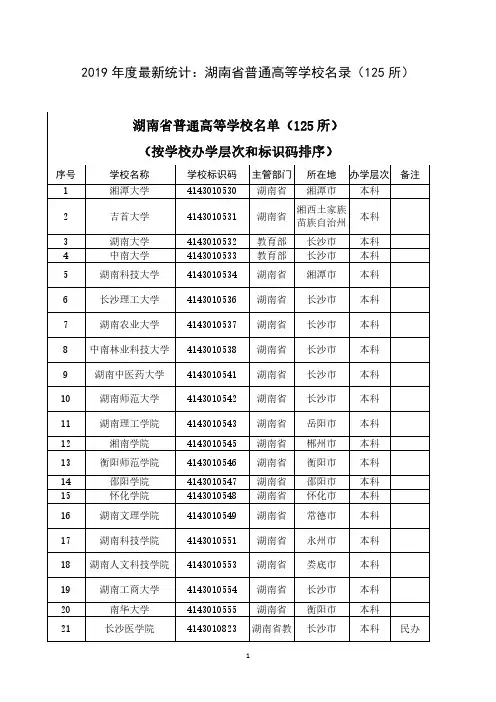
2019年度最新统计：湖南省普通高等学校名录（125所）湖南省普通高等学校名单（125所）（按学校办学层次和标识码排序）序号学校名称学校标识码主管部门所在地办学层次备注1湘潭大学4143010530湖南省湘潭市本科2吉首大学4143010531湖南省湘西土家族苗族自治州本科3湖南大学4143010532教育部长沙市本科4中南大学4143010533教育部长沙市本科5湖南科技大学4143010534湖南省湘潭市本科6长沙理工大学4143010536湖南省长沙市本科7湖南农业大学4143010537湖南省长沙市本科8中南林业科技大学4143010538湖南省长沙市本科9湖南中医药大学4143010541湖南省长沙市本科10湖南师范大学4143010542湖南省长沙市本科11湖南理工学院4143010543湖南省岳阳市本科12湘南学院4143010545湖南省郴州市本科13衡阳师范学院4143010546湖南省衡阳市本科14邵阳学院4143010547湖南省邵阳市本科15怀化学院4143010548湖南省怀化市本科16湖南文理学院4143010549湖南省常德市本科17湖南科技学院4143010551湖南省永州市本科18湖南人文科技学院4143010553湖南省娄底市本科19湖南工商大学4143010554湖南省长沙市本科20南华大学4143010555湖南省衡阳市本科21长沙医学院4143010823湖南省教长沙市本科民办育厅22长沙学院4143011077湖南省长沙市本科23湖南工程学院4143011342湖南省湘潭市本科24湖南城市学院4143011527湖南省益阳市本科25湖南工学院4143011528湖南省衡阳市本科26湖南财政经济学院4143011532湖南省长沙市本科27湖南警察学院4143011534湖南省长沙市本科28湖南工业大学4143011535湖南省株洲市本科29湖南女子学院4143011538湖南省长沙市本科30湖南第一师范学院4143012034湖南省长沙市本科31湖南医药学院4143012214湖南省怀化市本科32湖南涉外经济学院4143012303湖南省教育厅长沙市本科民办33湘潭大学兴湘学院4143012599湖南省教育厅湘潭市本科民办34湖南工业大学科技学院4143012604湖南省教育厅株洲市本科民办35湖南科技大学潇湘学院4143012649湖南省教育厅湘潭市本科民办36南华大学船山学院4143012650湖南省教育厅衡阳市本科民办37湖南工商大学北津学院4143012651湖南省教育厅长沙市本科民办38湖南师范大学树达学院4143012652湖南省教育厅长沙市本科民办39湖南农业大学东方科技学院4143012653湖南省教育厅长沙市本科民办40中南林业科技大学涉外学院4143012656湖南省教育厅长沙市本科民办41湖南文理学院芙蓉学院4143012657湖南省教育厅常德市本科民办42湖南理工学院南湖学院4143012658湖南省教育厅岳阳市本科民办43衡阳师范学院南岳学院4143012659湖南省教育厅衡阳市本科民办44湖南工程学院应用技术学院4143012660湖南省教育厅湘潭市本科民办45湖南中医药大学湘杏学院4143012661湖南省教育厅长沙市本科民办46吉首大学张家界学院4143012662湖南省教育厅张家界市本科民办47长沙理工大学城南学院4143013635湖南省教育厅长沙市本科民办48长沙师范学院4143013806湖南省长沙市本科49湖南应用技术学院4143013809湖南省教育厅常德市本科民办50湖南信息学院4143013836湖南省教育厅长沙市本科民办51湖南交通工程学院4143013924湖南省教育厅衡阳市本科民办52湘中幼儿师范高等专科学校3643000496湖南省邵阳市专科53长沙民政职业技术学院4143010827湖南省长沙市专科54湖南工业职业技术学院4143010830湖南省长沙市专科55株洲师范高等专科学校4143010836湖南省株洲市专科56湖南信息职业技术学院4143010865湖南省长沙市专科57湖南税务高等专科学校4143011601湖南省长沙市专科58湖南冶金职业技术学院4143011604湖南省株洲市专科59长沙航空职业技术学院4143012055总装备部长沙市专科60湖南大众传媒职业技术学院4143012300湖南省长沙市专科61永州职业技术学院4143012301湖南省永州市专科62湖南铁道职业技术学院4143012302湖南省株洲市专科63湖南科技职业学院4143012304湖南省长沙市专科64湖南生物机电职业技术学院4143012343湖南省长沙市专科65湖南交通职业技术学院4143012397湖南省长沙市专科66湖南商务职业技术学院4143012401湖南省长沙市专科67湖南体育职业学院4143012423湖南省长沙市专科68湖南工程职业技术学院4143012425湖南省长沙市专科69保险职业学院4143012596湖南省长沙市专科70湖南外贸职业学院4143012597湖南省长沙市专科71湖南网络工程职业学院4143012598湖南省长沙市专科72邵阳职业技术学院4143012600湖南省邵阳市专科73湖南司法警官职业学院4143012601湖南省长沙市专科74长沙商贸旅游职业技术学院4143012603湖南省长沙市专科75湖南环境生物职业技术学院4143012739湖南省衡阳市专科76湖南邮电职业技术学院4143012845湖南省长沙市专科77湘潭医卫职业技术学院4143012846湖南省湘潭市专科78郴州职业技术学院4143012847湖南省郴州市专科79娄底职业技术学院4143012848湖南省娄底市专科80张家界航空工业职业技术学院4143012849湖南省张家界市专科81长沙环境保护职业技术学院4143013031湖南省长沙市专科82湖南艺术职业学院4143013032湖南省长沙市专科83湖南机电职业技术学院4143013033湖南省长沙市专科84长沙职业技术学院4143013036湖南省长沙市专科85怀化职业技术学院4143013037湖南省怀化市专科86岳阳职业技术学院4143013038湖南省岳阳市专科87常德职业技术学院4143013039湖南省常德市专科88长沙南方职业学院4143013041湖南省教育厅长沙市专科民办89潇湘职业学院4143013042湖南省教育厅娄底市专科民办90湖南化工职业技术学院4143013043湖南省株洲市专科91湖南城建职业技术学院4143013044湖南省湘潭市专科92技术学院4143013045湖南省岳阳市专科93湖南中医药高等专科学校4143013802湖南省株洲市专科94湖南民族职业学院4143013804湖南省岳阳市专科95湘西民族职业技术学院4143013805湖南省湘西土家族苗族自治州专科96湖南财经工业职业技术学院4143013807湖南省衡阳市专科97益阳职业技术学院4143013808湖南省益阳市专科98湖南工艺美术职业学院4143013921湖南省益阳市专科99湖南九嶷职业技术学院4143013922湖南省教育厅永州市专科民办100湖南理工职业技术学院4143013923湖南省湘潭市专科101湖南软件职业学院4143013925湖南省教育厅湘潭市专科民办102湖南汽车工程职业学院4143013937湖南省株洲市专科103长沙电力职业技术学院4143013938湖南省长沙市专科104湖南水利水电职业技术学院4143013939湖南省长沙市专科105湖南现代物流职业技术学院4143013940湖南省长沙市专科106湖南高速铁路职业技术学院4143013941湖南省衡阳市专科107湖南铁路科技职业技术学院4143013942湖南省株洲市专科108学院4143014025湖南省长沙市专科109湖南电气职业技术学院4143014071湖南省湘潭市专科110湖南外国语职业学院4143014072湖南省教育厅长沙市专科民办111益阳医学高等专科学校4143014097湖南省益阳市专科112湖南都市职业学院4143014121湖南省教育厅长沙市专科民办113湖南电子科技职业学院4143014122湖南省教育厅长沙市专科民办114湖南国防工业职业技术学院4143014182湖南省湘潭市专科115湖南高尔夫旅游职业学院4143014309湖南省教育厅常德市专科民办116湖南工商职业学院4143014310湖南省教育厅衡阳市专科民办117湖南三一工业职业技术学院4143014322湖南省教育厅长沙市专科民办118长沙卫生职业学院4143014358湖南省长沙市专科119湖南食品药品职业学院4143014359湖南省长沙市专科120湖南有色金属职业技术学院4143014360湖南省株洲市专科121湖南吉利汽车职业技术学院4143014406湖南省教育厅湘潭市专科民办122湖南幼儿师范高等专科学校4143014468湖南省常德市专科123湘南幼儿师范高等专科学校4143014495湖南省郴州市专科124学院4143014508湖南省长沙市专科125怀化师范高等专科学校4143014663湖南省怀化市专科。

湖南省教育厅关于表彰全省普通高等学校优秀教研室的通报正文：---------------------------------------------------------------------------------------------------------------------------------------------------- 湖南省教育厅关于表彰全省普通高等学校优秀教研室的通报（湘教通[2010]421号）各普通高等学校：根据《关于2010年评选普通高等学校优秀教研室的通知》（湘教通〔2010〕350号）精神，我厅组织了全省普通高等学校优秀教研室评选工作。

在各高校开展校级优秀教研室评选的基础上，经学校推荐，我厅组织专家评选，确定国防科技大学基础物理教研室等101个教研室为全省普通高等学校优秀教研室。

希望受表彰的教研室继续发扬成绩，在组织教学中发挥示范带头作用，不断取得新的成绩。

全省各普通高等学校要牢固树立育人为本的办学理念，坚持教学工作的中心地位，进一步加强教学基层组织建设，规范教研室的设置和教学管理职能，采取切实有效的措施提高教师的教育教学水平，努力提高教学质量。

附件：湖南省普通高等学校优秀教研室名单二○一○年十一月二十日附件：湖南省普通高等学校优秀教研室名单序号学校名称教研室名称1国防科技大学基础物理教研室2国防科技大学控制理论与控制工程教研室3国防科技大学大学英语教研室4国防科技大学军事理论教研室5中南大学物理化学教研室6中南大学无机材料教研室7中南大学软件工程教研室8中南大学工业训练教研室9中南大学儿科学教研室10中南大学传染病学教研室11中南大学生理学教研室12湖南大学机械设计教研室13湖南大学管理科学教研室14湖南大学应用金融教研室15湖南大学化工院实验教学中心教研室16湖南大学通信工程教研室17湖南大学英语专业教研室18湖南师范大学“读议写”教研室19湖南师范大学钢琴教研室20湖南师范大学古代汉语教研室21内科教研室22湖南师范大学伦理学教研室23湘潭大学比较文学与世界文学教研室24湘潭大学电子政务教研室25湘潭大学技术物理教研室26湘潭大学环境工程教研室27长沙理工大学物理学教研室28长沙理工大学概率与运筹教研室29长沙理工大学大学英语第二教研室30长沙理工大学企业管理教研室31食品科学与工程教研室32湖南农业大学生态学教研室33湖南农业大学植物保护教研室34湖南农业大学动物药学教研室35中南林业科技大学木材科学与工程教研室36中南林业科技大学市场营销教研室37中南林业科技大学森林培育教研室38中南林业科技大学心理健康教育教研室39湖南中医药大学中药鉴定教研室40南华大学建筑环境与热能工程教研室41南华大学核技术教研室42南华大学病理生理学教研室43南华大学内科学教研室44湖南科技大学采矿工程教研室45湖南科技大学测控技术与仪器教研室46湖南科技大学生物科学教研室47湖南科技大学经济学教研室48吉首大学民族传统体育教研室49吉首大学数学与应用数学教研室50吉首大学工商管理教研室51包装设计教研室52湖南工业大学英语专业基础英语教研室53湖南商学院金融学教研室54湖南商学院会展经济与管理教研室55湖南理工学院体育理论教研室56湖南理工学院化学基础教研室57衡阳师范学院经济理论教研室58衡阳师范学院田径教研室59湖南文理学院地理科学教研室60湖南文理学院农学教研室61机械制造及其自动化教研室62湖南工程学院自动化教研室63湖南城市学院基础化学教研室64湖南城市学院田径体操武术综合教研室65邵阳学院英语专业教研室66邵阳学院食品质量与安全教研室67怀化学院电子信息教研室68怀化学院信息与计算科学教研室69湖南科技学院信息技术基础教研室70湖南科技学院化学教研室71网络教研室72湘南学院大学英语第三教研室73湖南人文科技学院大学物理教研室74湖南人文科技学院武术体操田径教研室75长沙学院软件工程教研室76长沙学院材料成型及控制工程专业教研室77湖南涉外经济学院计算机基础教研室78湖南涉外经济学院高尔夫教研室79长沙医学院临床生物化学检验教研室80湖南工学院机械制图教研室81体育教研室82湖南第一师范学院计算机科学与技术教研室83湖南第一师范学院文史教研室84湖南财政经济学院大学英语二教研室85湖南警察学院治安管理教研室86湖南女子学院服装设计教研室87湘潭大学兴湘学院应用化学教研室88长沙理工大学城南学院计算机基础教研室89湖南农业大学东方科技学院大学英语教研室90中南林业科技大学涉外学院数学教研室91湖南科技大学潇湘学院计算机应用教研室92湖南工业大学科技学院经济管理教研室93湖南理工学院南湖学院制药工程教研室94湖南文理学院芙蓉学院计算机基础教研室95衡阳师范学院南岳学院音乐理论教研室96湖南工程学院应用技术学院电气工程及其自动化教研室97怀化医学高等专科学校人体解剖学教研室98湖南中医药高等专科学校针灸推拿教研室99邵阳医学高等专科学校生物化学及检验教研室100长沙师范学校英语教育教研室101益阳医学高等专科学校英语教研室——结束——。

湖南省2022年普通高等学校对口招生考试数学试卷本试题卷包括选择题、填空题和解答题三部分,共5页。

时量120分钟。

满分120分。

一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U ={1,3,5,7},集合A ={3,5},则C U A =A.{1,7}B.{1,5}C.{3,7}D.{5,7}2.“(x +1)(x -3)=0”是“x =3”的A.充分不必要条件B.必要不充分条件C.充分且必要条件D.既不充分也不必要条件3.已知cos α=−31,且α∈(-π,0),则sin α=A.322-B.32 C.322 D.−324.下列函数中既是偶函数,又在区间(0,+∞)上单调递增的是A.y =cos xB.y =4xC.y =2x 2+1D.y =ln x5.已知sin 2x =a -1,则实数a 的取值范围是A.[-1,1]B.[0,1]C.[0,2]D.[-2,0]6.已知向量a =(2,-1),b =(-3,4),则a ·(2b -a )=A.-25B.-10C.10D.257.不等式|2x +5|>7的解集是A.(-6,1)B.(-∞,-6)∪(1,+∞)C.(-1,6)D.(-∞,-1)∪(6,+∞)8.已知a =0.90.9,b =0.91.8,c =1.80.9,则a ,b ,c 的大小关系是A.b <c <aB.a <c <bC.a <b <cD.b <a <c9.已知两条不同的直线m ,n 与平面α,则下列命题正确的是A.若m //α,n //α,则m //nB.若m ⊥n ,m//α,则n ⊥αC.若m ⊥n ,m ⊥α,则n ⊥αD.若m ⊥α,n ⊥α,则m //n10.已知点P 在直线l :x -y -6=0上,点Q 在圆O :x 2+y 2=2上,则|PQ |的最小值为A.24B.23C.22D.2二、填空题(本大题共5小题,每小题4分,共20分)11.在一次“党史”知识竞赛中,参加知识竞赛的10名学生的成绩如下表:成绩92959698人数1243则这10名学生的平均成绩是.12.经过点M (0,-2),且与直线x +y +1=0平行的直线方程为.13.若角α的终边经过点P (21，−23),则sin 2α=.14.如图,高为5cm,底面边长是3cm 的正四棱柱形工件,以它的两底面中心的连线为轴,钻出一个直径是2cm 的圆柱形孔,则剩余部分几何体的体积是____cm 3(圆周率π取3.14).(第14题)15.若数列{a n }满足a 1=1,且a n +1=2a n +1,则数列{a n }的通项公式a n =.三、解答题(本大题共7小题,其中第21,22小题为选做题,满分60分.解答应写出文字说明、证明过程或演算步骤)16.(本小题满分10分)已知函数f (x )=1+log 4(x +m ),f (1)=2.(1)求实数m 的值,并写出f (x )的定义域;(2)若f (x )<3,求x 的取值范围.、已知等差数列{a n}满足a1=1,a5-a3=4.(1)求a10;(2)设数列{a n}的前n项和为S n,问:S4,S8,S16是否成等比数列?请说明理由.18.(本小题满分10分)某班拟组织部分学生参观爱国主义教育基地.已知该班第一小组有5名男生与3名女生,从中任意选取3名学生去参观.(1)用ξ表示选取的3人中女生的人数,求ξ的分布列；(2)求选取的3人中,女生人数多于男生人数的概率.如图,在三棱锥P -ABC 中,PA ⊥平面ABC ,AB ⊥B C.(1)证明:平面PBC ⊥平面PAB ;(2)若AB =BC =2,直线PB 与平面ABC 所成的角为60°,求三棱锥P -ABC 的体积.（第19题）20.(本小题满分10分)已知双曲线C ：12222=-by a x =1(a ,b >0)的离心率为26,左、右焦点分别为F 1,F 2,且|F 1F 2|=23(1)求双曲线C 的方程;(2)设直线y =x +3与双曲线C 相交于M ,N 两点,求MNF 2的面积.选做题:请考生在第21,22题中选择一题作答.如果两题都做,则按所做的第21题计分,作答时,请写清题号.21.(本小题满分10分)如图,点D为等边三角形ABC的边BC上一点,且BD=2DC,AD=7.(1)求CD的长;(2)求sin∠BAD的值.(第21题)22.(本小题满分10分)某工厂生产甲、乙两种电子产品,每生产一件甲产品需要A,B配件分别为4件和2件;每生产一件乙产品需要A,B配件分别为4件和6件.该厂每天可从配件厂最多获得A配件20件和B 配件18件,且生产一件甲产品的利润为4千元,生产一件乙产品的利润为5千元.问如何安排生产,才能使工厂每天利润最大?并求出利润的最大值.湖南省2022年普通高等学校对口招生考试数学试卷参考答案一、选择题1.A2.B3.A4.C5.C6.A7.B8.D9.D10.C二、填空题11.9612.02=++y x 13.23-14.29.315.12-n三、解答题16.解：（1）)3(log 1)(32)1(log 1)1(44++=∴=⇒=++=x x f m m f 函数)(.3-)(303∞+->⇒>+，的定义域为即x f x x （2）1316316log 2)3(log )3(log 1)(444<⇒<+⇒=<+⇒++=x x x x x f )()(.133-3)(3-)(，的取值范围为时，的定义域为又x x f x f <∴∞+ 17.解：（1）.19291924211035=⨯+=+=∴=⇒==-d a a d d a a （2）在等差数列{}n a 中.,,S 2562120116120161516211664228182887821816261464342141684164281116118114成等比数列S S S S S d a d a S d a d a S d a d a S ∴⋅==⨯+⨯=+=⨯⨯⨯+==⨯+⨯=+=⨯⨯⨯+==⨯+⨯=+=⨯⨯⨯+=18.解：（1）ξ可分别取0,1,2,3.561)3(5615)2(28155630)1(2855610)0(38333823153813253835==============C C P C C C P C C C P C C P ξξξξξ的分布列为ξ123P28528155615561（2）女生人数多于男生人数的概率为725615615)3()2(=+==+=ξξP P 19.解：（1）BCPA ABC⊥∴⊥平面P A PABPBC 平面平面平面则又⊥∴⊥=⋂⊥P ABBC AP A AB BC AB （2）60=∠∴⊥PBA ABC PB ABC P A 所成角即为与平面直线平面33432222131S 3132tan ABC -=⨯⨯⨯⨯===<⋅=h V PBA AB P A P AB ABC P 中，在直角三角形20.解：（1）3322F F 21=⇒==c c 12C 123226322222=-=-=-==⇒===y x a c b a a a c e 的方程为即双曲线（2）设M 、N 两点的坐标分别为()()2211,,,y x y x 3462421216)1(13032484)34(24)(183402834123222222122122121222=⨯⨯===-++-==⨯--=-++==-=+=++⇒⎪⎩⎪⎨⎧=-+=∆d MN S d F x x x x k MN x x x x x y x x y MNF 到直线的距离根据韦达定理可得21.解：（1）设AB 长为a ,则BD=a 32，DC=a 31在等边三角形ABC 中，131360cos 322)32(7cos 2222222===⇒⋅⋅-+=⇒⋅-+=︒a CD a a a a a BBD AB BD AB AD 则（2）在三角形ABD 中，根据正弦定理可得721sin sin sin sin =∠=∠⇒∠=∠AD B BD BAD B AD BAD BD 22.解：设生产甲产品为x 件，乙产品为y 件，公司获利为Z 元，则z =4000x +5000y由题意得：⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+⇒⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+009350018622044y x y x y x y x y x y x 如右图所示，当x =3,y =2时，Z max =4000×3+5000×2=22000（元）答：生产甲产品为3件，乙产品为2件时，公司获利最大为22000元.x+y=5yx x+3y=9o 、A （3,2）59534x+5y=0。

湖南商学院友好合作湖南财政）湖南商学院湖南商学院是一所以、为主，涵盖经、管、法、文、理、工等学科的多科性省属全日制普通高等院校，是教育部优秀高校。

2008年，成为学位授予权立项建设单位。

学校位于历史文化名城长沙市，南朝岳麓，东顾湘江，交通便利，环境优美。

学校始建于1949年，校园占地面积亩。

中文名：商学院外文名：Hunan University ofCommerce校训：厚德、博学、精明、自强创办时间：1949年12月26日类别：学校类型：主管部门：湖南省教育厅现任校长：所属地区：湖南主要院系：经济与贸易学院、财政金融学院、学院、会计学院等硕士点：3个学校简介湖南商学院（英文名：Hunan University of Commerce）湖南商学院是由湖南省人民政府领导管理的全日制普通本科院校，由原湖南商业高等专科学校和湖南省商业管理干部学院合并组建而成，是湖南省经济和社会发展中重点扶持的高等院校之一。

学校位于历史文化名城市，南朝岳麓，东顾，交通便利，环境优美。

学校现设有16个教学院、部和28个科研机构以及首批批准成立的独立学院--。

设有33个本科湖南商学院学院景色(20张)专业，现有省级重点学科1个，省级重点建设学科3个，省级重点专业5个，国家级精品课程2门，省级精品课程4门，在校学生达17000余人。

校训厚德、博学、精明、自强学校东校门历史沿革1950-1966年，湖南省商业厅会计人员训练班到商业厅干部学校阶段，先后经历了商业厅会计人员训练班、湖南省财经干部训练班商干大队，湖南贸易学校、湖南商业干部学校，到1958年12月，五所干校合并成历史沿革(2张)财贸干校，1960年改为财贸学院，1963年11月，省委办公厅批复恢复省商业干校。

1971-1982年，湖南省商业学校阶段。

文化大革命后于1971年复校。

1972年4月，由省革委会批准成立湖南省商业学校，1973年作为普通中专学校面向社会招生。

湖南省2021年普通高等学校对口招生考试数学本试题卷包括选择题、填空题和解答题三部分.共4页，时量120分钟，满分120分一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知集合{}53,1，=A ,{}432,1，，=B ，且=B A A.{}3,1 B.{}53,1， C.{}432,1，， D.{}5432,1，，，=A 2.函数）（x x f +=1log )(3的定义域为A.()1--，∞ B.()∞+，1- C.[)∞+，1- D.()∞+，03.函数14)(2--=x x x f 的单调递减区间是A.[)∞+，2 B.[)∞+，2- C.(]2-，∞ D.(]4-，∞4.为了得到函数)4sin(π+=x y 的图象，只需要x y sin =将的图象A.向上平移4π个单位 B.向左平移4π个单位C.向下平移4π个单位 D.向右平移4π个单位5.点)1-,0(到直线0143=+-y x 的距离为A.52 B.53 C.54 D.16.不等式312<-x 的解集是A.}2|{<x x B.}1|{->x x C.}21|{<<-x x D.}21|{>-<x x x 或7.“1=x ”是“0232=+-x x ”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件8.若d c b a >>,则A.db c a +>+ B.db c a --> C.bd ac > D.bcad >9.设m,n 为两条不同的直线，βα,为两个不同的平面，则下列结论正确的是()A.若α//,//n n m ,则α//mB.若βα//,//,//n m n m ,则βα//C.若,,,βαβα⊂⊂⊥n m ,则nm ⊥ D.若,,,βα⊥⊥⊥n m n m ,则βα⊥10.已知某地区中小学生人数和近视情况分别如图（1）和图（2）所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则在抽取的高中生中，近视人数约为A.1000B.40C.27D．20二、填空题（本大题共5小题，每小题4分，共20分）11.已知3tan -=α，且α为第四象限角，则=αcos .12.已知向量()2,1-=a ，()1,3-=b ，则=+b a 2.13.621⎪⎭⎫ ⎝⎛+x x 展开式的常数项为（用数字作答）.14.过圆0422=-+x y x 的圆心且与直线02=+y x 垂直的直线方程为.15.已知函数))((R x x f ∈为奇函数，2)(3)(+=x f x g .若2-)-9(=g ，则=)9(g .三、解答题（本大题共7小题，其中第21，22小题为选做题．满分60分.解答应写出文字说明、证明过程或演算步骤）16.（10分）已知各项为正数的等比数列{}n a 中，11=a ，43=a .（1）求数列{}n a 的通项公式;（2）设n n a b 2log =，求数列{}n b 的前n项和n S .17.（10分）端午节吃粽子是我国的传统习俗.设一盘中装有6个粽子，其中肉粽1个，蛋黄粽2个，豆沙粽3个，这三种粽子的外观完全相同，从中任意选取2个.（1）用ξ表示取到的豆沙粽的个数，求ξ的分布列;（2）求选取的2个中至少有1个豆沙粽的概率。

湖南省2024年普通高等学校对口招生考试建筑类专业综合知识试题本试题卷共六大题，43道小题，共6页。

时量150分钟，满分390分。

一、单选题（在本题的每一小题的备选答案中，只有一个答案是正确的，本大题共25小题，每小题4分，共100分）1.某实训室的柱下基础为钢筋混凝土独立基础，该摧础的混凝土工程属于A.单项工程B.单位工程C.分部工程D.分项工程2.某施工段的土方工程量为400m3，安排两班制施工，每班20人，每人每天完成1m3的土方工程量，则该队伍在该施工段上的流水节拍为A.10天B.8天C.6天D.4天3.某三层办公楼工程，每层划分为两个施工段，组织两个施工队进行等节奏流水施工，流水节拍为3天，则工期为A.24天B.21天C.18天D.15天4.某网络计划中A工作有两项紧后工作B和C，A工作的最迟开始时间为第6天，B、C工作的最迟完成时间分别为第24天和第25天，B工作的持续时间为10天，C工作的持续时间为12天，则A工作的持续时间为A.8天B.7天C.6天D.5天5.采用轻型井点降水法降低基坑地下水位时，应将基坑内地下水位降至基坑底面以下不小于A.0.5mB.0.8mC.1.0mD.1.2m6.用水准仪测量地面点的高程，经测定，A、B两点的高差为+1.75m，已知A点高程为321.25m，则B点高程为A.319.50mB.321.25mC.322.25mD.323.00m7.用经纬仪测量水平角，盘左读数分别为0o 00' 20”、34o 45' 56”，盘右读数分别为180o 00' 30”、214o 45' 58”，则该一测回角值为A.34o45' 28”B.34o45' 32”C.34o 45' 36“D.34o45' 56”8.在混凝土施工缝处继续浇筑混凝土时，对于柱墙水平施工缝，应先铺设一层水泥砂浆接浆层，该水泥砂浆接浆层厚度不应大于A.20 mmB.30 mmC.40 mmD.50 mm9.装配式构件脱模起吊时，其混凝土立方体抗压强度应满足设计要求，且不应小于A.5 MPaB.10 MPaC.15 MPaD.20 MPa10.《工程结构通用规范>规定，普通房屋结构设计工作年限不得低于A.5年B.50年C.70年D.100年11.光圆钢筋的牌号为A.HPB300B.HRB400C.HRBF400D.HRB50012.梁下部纵筋直径为20mm，则梁下部纵筋水平方向净距不应小于A.20mmB.25mmC.30mmD.40mm13.四边支承的现浇混凝土板，长边长度为8m，短边长度为2m，根据板长短边长度的比值，该板为A.单向板B.双向板C.悬挑板D.预制板14.关于多层砌体房屋的结构体系要求，下列说法正确的是A.优先采用纵墙承重结构体系B.楼梯间应设置在房屋的尽端和转角处C.纵横墙布置沿平面内宜对齐，沿竖向应上下连续D.横墙较少、跨度较大的房屋，优先采用预制楼板15.下列连接方式，不能用于钢结构连接的是A.焊接连接B.螺栓连接C.铆钉连接D.套筒连接16.“三水准”抗震设防目标是指A.小震不坏、中震可修、大震不倒B．小震可修、中震不坏、大震不倒C.小震不倒、中震可修、大震不坏D.小震不坏、中震不倒、大震可修17.当地基土潮湿或有地下水时，砌筑砖基础应采用A.混合砂浆B.石灰砂浆C.水泥砂浆D.砌块专用砂浆18.关于预制商品混凝土外墙构件，下列说法错误的是A.施工周期长B.质量可靠C.工业化程度高D.节能环保19.剪力墙平法施工图中，代号YBZ表示A.约束边缘柱B.约束边缘构件C.构造边缘柱D.构造边缘构件20.在建筑施工图中，细虚线可以用于A.中心线B.对称线C.定位轴线D.图例填充线21.下列建筑构件，属于难燃烧体的是A.木板B.大理石板C.沥青混凝土板D.不锈钢板22.下列踏步尺寸，不适宜用于室外台阶的是A.300mm×150mmB.280mm×165mmC.350mm×125mmD.330mm×140mm23.在建筑中设置沉降缝，是考虑到A.地震的影响B.气候的影响C.地基不均匀沉降的影响D.建筑施工的影响24.为防止雨水流入室内，要求阳台地面低于室内地面A.10~20mmB.20~30mmC.30~40mmD.40~50mm25.楼梯段踏步的数量一般不宜超过A.17级B.18级C.19级D.20级二、简答题（本大题共5小题，每小题8分，共40分）26.简述单层现浇钢筋混凝土框架结构房屋主体工程的施工顺序。

湖南⼯商⼤学是211还是985
不是985⼤学，也不是211⼤学。

湖南⼯商⼤学位于湖南省长沙市，是⼀所以经济学、管理学为主，涵盖经、管、⼯、理、法、⽂、艺等学科的省属全⽇制普通⾼等学校，湖南省国内⼀流学科建设⾼校。

湖南⼯商⼤学
学校源起于1949年12⽉成⽴的长沙市军管会贸易处⼲部训练班，1994年经原国家教委批准，由湖南省商业管理⼲部学院和湖南商业⾼等专科学校合并成⽴湖南商学院。

2013年，学校成为硕⼠学位授予权单位。

2019年6⽉，更名为湖南⼯商⼤学。

截⾄2021年5⽉，学校占地1432.08亩，建筑⾯积57万余平⽅⽶，教学、科研仪器设备总值1.9亿余元，图书馆藏书近200万册；设有14个教学院（部）、91个科研机构，开办55个本科专业，拥有10个⼀级学科硕⼠学位授权点、8个硕⼠专业学位授权点；有普通全⽇制在校学⽣1.9万余⼈、教职⼯1464⼈。

湖南⼯商⼤学王牌专业
教育部⾼等学校“第⼀类特⾊专业建设点”：国际经济与贸易、市场营销
教育部⾼等学校“第⼆类特⾊专业建设点”：经济学
省级特⾊专业：⾦融学、法学、艺术设计、会计学、财务管理、信息管理与信息系统、国际经济与贸易、市场营销、经济学
省级重点专业：⼯商管理、旅游管理、国际经济与贸易、市场营销、经济学
省级资助建设专业：物流管理、电⼦信息⼯程。

湖南省2020年普通高等学校对口招生考试数学本试卷包括选择题、填空题和解答题三部分，共4页。

时量120分钟。

满分120分。

一、选择题（本大题共10小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知集合}{a A ,1=,}{4,3,2,1=B ,}{4,1=⋂B A ,则=a A.1 B.2 C.3 D.42.=120sin A.21B.21-C.23 D.23-3.”“1=x 是”“012=-x 的A.充分必要条件 B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件4.点),3(),3,1(t N M 在函数xky =的图像上,则t 的值为A.1 B.3C.6D.95.平行四边形ABCD 中,AC 与BD 交于点M ,a =AB ,b =AD ,则=AM A.b 2121-a B.b 2121+a C.b +a D.b-a 6.函数)1(log )(2-=x x f 定义域为A.}{0|>x x B.}{1|≠x xC.}{2|>x x D.}{1|>x x 7.61(xx -展开式中的常数项为A.-20B.20C.-120D.1208.已知20sin =a ,40cos =b ,80tan =c ,则a ,b ,c 的大小关系为A.c b a >>B.a c b >>C.ab c >> D.ba c >>9.已知函数xx f 2)(=.若)2()2(f a f <-,则a 的取值范围是A.)2,2(-B.)4,0(C.),4()0,(+∞-∞ D.)4,(-∞10.如图是正方形的平面展开图，则在这个正方体中：①BM 与ED 平行.②CN 与BM 成60角.③CN 与BE 垂直.④DM 与BN 是异面直线.以上四个命题中，正确的命题个数为A.1 B.2（10题图）C.3D.4二、填空题（本大题共5个小题，每小题4分，共20分）11.已知向量)2,1(=a ,)3,2(-=b ,则=⋅b a .12.某校有男生300人,平均身高为cm 173,女生200人,平均身高为cm 163,则该校所有学生的平均身高为cm .13.函数8cos 2-=x y 的最小值为.14.已知等差数列}{n a 的前n 项和为n S ，且161=a ,132=a ,则=5S .15.过点P(2,1)作圆122=+y x 的两条切线，切点分别为A ,B ,则AB 所在直线方程为.三、解答题（本大题共7小题，其中21，22为选做题。

湖南2023年普通高等学校招生体检通知湖南2023年普通高等学校招生体检近日，湖南省教育考试院发布《关于做好2023年普通高等学校招生体检工作的通知》(以下简称《通知》)，根据相关安排，湖南省2023年高考体检工作统一要求在3月28日之前完成，具体时间由市(州)招生考试机构自行安排。

按照国家和湖南省有关规定，凡报名参加2023年普通高等学校招生考试(包括统考生、单考生、强基计划、保送生、高水平艺术团、高水平运动队、推荐免试生、各类单招、省内公费定向对口招生师范生、中职技能竞赛获奖免试生以及准备参加2023年高职单招的退役军人、农民工、下岗失业人员、新型职业农民、企业在岗人员等五类社会人员)的所有考生均须参加体检，且须参加规定要求的所有项目检查，并如实填写本人既往病史。

不参加体检或体检项目不完整，影响考生后续录取的，由考生本人承担后果。

2023年高考体检标准按教育部、卫生部、中国残疾人联合会颁发的《普通高等学校招生体检工作指导意见》(教学〔2003〕3号)，教育部办公厅、卫生部办公厅《关于普通高等学校招生学生入学身体检查取消乙肝项目检测有关问题的通知》(教学厅〔2010〕2号)以及教育部高校学生司《关于明确慢性肝炎病人并且肝功能不正常的具体判定标准的函》(教学司函〔2010〕22号)等文件执行。

对体检结果有异议的考生可以提出复检申请。

复检工作由各市(州)招生考试机构自行组织安排，复检工作须在4月8日前完成。

对复检结果仍有异议的考生可以提出仲裁申请，考生须于4月15日前到所在市(州)招生考试机构提出对复检结果的仲裁申请，省教育考试院负责协调终检医院对有异议的体检结论做出最终裁定。

2023年高考体检信息采集采用电子采集导入方式与纸质录入采集方式两种方式。

其中，电子采集导入方式由体检医院在体检过程中直接通过电子设备采集考生体检数据信息，体检数据须每天进行备份刻盘，体检完成后县(市、区)招生考试机构将体检数据信息按照系统要求格式统一导入系统，并将每天备份的数据光盘上交我院普通高校招生处;纸质录入采集方式由县(市、区)招生考试机构将经体检医院或相应的医疗单位盖章确认后的体检表汇总，安排人员通过系统录入考生的体检信息。

2021湖南各学校招生计划2021年湖南省普通高等学校招生计划如下：
一、招生范围
1.招收全日制本科生；
2.招收非全日制本科生；
3.招收专科自考生；
4.招收硕士研究生；
5.招收博士研究生；
6.招收社会技术学士学位研究生；
7.招收函授生；
8.招收远程教育生；
9.招收成人教育生；
10.招收外国留学生；
11.招收其他学历生。

二、招生对象
1.招收中华人民共和国公民；
2.招收外国公民；
3.招收港澳台地区学生；
4.招收其他持有合法居留资格的外国公民。

三、招生方式
1.统一招生：按照国家统一规定的招生办法，统一招收考生；
2.单独招生：按照学校的招生办法，单独招收考生；
3.调剂招生：按照国家和学校的招生办法，调剂招收考生；
4.推荐招生：按照学校的招生办法，推荐招收考生；
5.社会招生：按照学校的招生办法，社会招收考生。

2024年普通高等学校招生全国统一考试考前演练二数学（答案在最后）注意事项：1.答卷前，考生务必将自己的姓名､考生号､考场号､座位号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3.考试结束后，将本试卷和答题卡一并交回.一､选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.已知{}{}20,1,2,0A B xx x ==+=∣，则A B ⋃为（）A.∅B.{}0C.{}0,1,2D.{}1,0,1,2-2.已知复数2i1iz +=+，则复数z 的实部与虚部之和为（）A.0B.1D.23.某骑行爱好者在专业人士指导下对近段时间骑行锻炼情况进行统计分析，统计每次骑行期间的身体综合指标评分x 与骑行用时y （单位：小时）如下表：身体综合指标评分()x 12345用时(/y 小时）9.58.87.876.1由上表数据得到的正确结论是（）参考数据：()()()()5552211110,7.06,8.4,8.402.ii i i i i i x x y y x xy y ===-=-=--=-∑∑∑.参考公式：相关系数()()niix x y y r --=∑.A.身体综合指标评分x 与骑行用时y 正相关B.身体综合指标评分x 与骑行用时y 的相关程度较弱C.身体综合指标评分x 与骑行用时y 的相关程度较强D.身体综合指标评分x 与骑行用时y 的关系不适合用线性回归模型拟合4.已知二项式(12)n x +（其中*n ∈N 且5n ）的展开式中3x 与4x 的系数相等，则n 的值为（）A.5B.6C.7D.85.已知函数()y f x =是定义在R 上的偶函数，对任意实数()(),2x f x f x -=.当[]1,2x ∈时.()21log f x x =-.则()21f 的值为（）A.0B.1C.21log 21- D.210log 21+6.已知点()4,1M ，抛物线22(0)y px p =>的焦点为,F P 为抛物线上一动点，当P 运动到()2,t 时，4PF =，则PM PF +的最小值为（）A.6B.5C.4D.37.湖南省衡阳市的来雁塔，始建于明万历十九年（1591年），因鸿雁南北迁徙时常在境内停留而得名.1983年被湖南省人民政府公布为重点文物保护单位.为测量来雁塔的高度，因地理条件的限制，分别选择C 点和一建筑物DE 的楼顶E 为测量观测点，已知点A 为塔底，A ，C ，D 在水平地面上，来雁塔AB 和建筑物DE 均垂直于地面（如图所示）.测得18m,15m CD AD ==，在C 点处测得E 点的仰角为30°，在E 点处测得B 点的仰角为60°，则来雁塔AB 的高度约为（）（ 1.732≈，精确到0.1m ）A.35.0mB.36.4mC.38.4mD.39.6m8.已知圆22:(4)4C x y -+=，点M 在线段()04y x x = 上，过点M 作圆C 的两条切线，切点分别为,A B ，以AB 为直径作圆C '，则圆C '的面积的最大值为（）A.πB.2πC.5π2D.3π二､多选题（本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.）9.已知函数()()πcos 202f x x ϕϕ⎛⎫=+-<< ⎪⎝⎭的图象经过点10,2P ⎛⎫⎪⎝⎭，则下列结论正确的是（）A.函数()f x 的最小正周期为πB.π3ϕ=-C.函数()f x 的图象关于点5π,06⎛⎫- ⎪⎝⎭中心对称D.函数()f x 在区间ππ,62⎛⎫⎪⎝⎭单调递减10.已知函数()f x 是定义域为R 的偶函数，()g x 是定义域为R 的奇函数，且()()2xf xg x e +=.函数()()()22F x f x mf x =-在[)0,∞+上的最小值为-2.则下列结论正确的是（）A.()e exxf x -=+ B.()g x 在实数集R 单调递减C.3m =D. 3.3m =-或13411.在棱长为2的正方体1111ABCD A B C D -中，M N ､分别是侧棱11BB CC ､的中点，P 是侧面11BCC B （含边界）内一点，则下列结论正确的是（）A.若点P 与顶点1C 重合，则异面直线1AA 与DP 所成角的大小为60B.若点P 在线段MN 上运动，则三棱锥11C PDB -的体积为定值C.若点P 在线段1B C 上，则1AP BD ⊥ D.若点P 为1BC 的中点，则三棱锥P ABC -的外接球的体积为82π3三､填空题（本大题共3小题，每小题5分，共15分.）12.在ABC 中，,AB c AC b == ，点M 满足(01)BM BC λλ=<<，若1233AM b c =+ ，则λ的值为__________.13.已知π1sin 65α⎛⎫-= ⎪⎝⎭，则πcos 23α⎛⎫- ⎪⎝⎭等于__________.14.已知12,F F 是椭圆C 的两个焦点，P 为椭圆C 上一点，且()121260,23F PF PF m PF m ∠==，则椭圆C 的离心率取值范围为__________.四､解答题（本大题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.）15.（本小题满分13分）已知等差数列{}n a 的前n 项和为n S ，且497,81a S ==.等比数列{}n b 是正项递增数列，且1231238,7b b b b b b =++=.（1）求数列{}n a 的通项n a 和数列{}n b 的通项n b ；（2）若1,,,,n n n n n a b n c a b n +-⎧=⎨⎩为奇数为偶数求数列{}n c 的前2n 项和.16.（本小题满分15分）如图1，在五边形ABCDP 中，连接对角线,AD AD∥,,224BC AD DC PA PD AD BC DC ⊥=====，将三角形PAD 沿AD 折起，连接,PC PB ，得四棱锥P ABCD -（如图2），且PB E =为AD 的中点，M 为BC 的中点，点N 在线段PE 上.（1）求证：平面PAD ⊥平面ABCD ；（2）若平面AMN 和平面PAB的夹角的余弦值为29，求线段EN 的长.17.（本小题满分15分）三人篮球赛是篮球爱好者的半场篮球比赛的简化版，球场为1511⨯米，比赛要求有五名球员.某高校为弘扬体育精神，丰富学生业余生活､组织“挑战擂王”三人篮球赛，为了增强趣味性和观赏性，比赛赛制为三局二胜制，即累计先胜两局者赢得最终比赛胜利（每局积分多的队获得该局胜利，若积分相同则加时决出胜负）.每局比赛中犯规次数达到4次的球员被罚出场（终止本场比赛资格）.该校的勇士队挑战“擂王”公牛队，李明是公牛队的主力球员，据以往数据分析统计，若李明比赛没有被罚出场，公牛队每局比赛获胜的概率都为34，若李明被罚出场或李明没有上场比赛，公牛队每局比赛获胜的概率都为12，设李明每局比赛被罚出场的概率为p 且11,62p ⎡⎤∈⎢⎥⎣⎦（1）若李明参加了每局的比赛，且13p =（i ）求公牛队每局比赛获胜的概率；（ii ）设比赛结束时比赛局数为随机变量X ，求随机变量X 的分布列和数学期望；（2）为了增强比赛的娱乐性，勇士队和公牛队约定：李明全程上场比赛，但若李明被罚出场，则李明将不参加后面的所有局次比赛.记事件A 为公牛队2：0获得挑战赛胜利，求事件A 的概率的最小值.18.（本小题满分17分）已知双曲线2222:1(0)x y E a b a b-=>>的左､右焦点为12F F ､，点()0P y 在双曲线E 的右支上.且124PF PF -=，三角形12PF F 的面积为（1）求双曲线E 的方程；（2）已知直线:1l x =与x 轴交于点M ，过M 作斜率不为0的直线12l l ､，直线1l 交双曲线E 于,A B 两点，直线2l 交双曲线E 于,C D 两点.直线AC 交直线l 于点G ，直线BD 交直线l 于点H .试证明：MG MH为定值，并求出该定值.19.（本小题满分17分）已知函数()2e 3(,0,e xf x a ax a a =-∈≠R 是自然对数的底数，e 2.71828)= .（1）当1a =时，求函数()f x 的零点个数；（2）当1a =时，证明：()cos 2f x x x - ；（3）证明：若[)1,,a x ∞∈+∈R ，则()12sin f x x - .2024年普通高等学校招生全国统一考试考前演练二数学参考答案一､选择题（本大题共8小题，每小题5分，共40分.）1.D 【解析】由{}20B xx x =+=∣，得{}0,1B =-，又集合{}0,1,2A =，所以{}1,0,1,2A B ⋃=-，故选D.2.B 【解析】因为()()()()2i 1i 2i 31i1i 1i 1i22z +-+===-++-，所以复数z 的实部与虚部之和31122⎛⎫+-= ⎪⎝⎭，故选B .3.C 【解析】因为相关系数()()51iix x y y r --=-∑.即相关系数近似为1,y -与x 负相关，且相关程度相当高，从而可用线性回归模型拟合y 与x 的关系.所以选项ABD 错误，C 正确.故选C.4.A【解析】因为*n ∈N 且5n ，由题意知33442C 2C n n =，得()()()()()3412123223!4!n n n n n n n -----⋅=⋅，求得5n =，故选A .5.B 【解析】由已知()y f x =为偶函数，所以()()f x f x -=，又()()2f x f x -=，所以()()2f x f x -=-，所以()()2f x f x +=，所以函数()f x 是周期为2的周期函数，()()()221210111log 11f f f =⨯+==-=.故选B.6.A 【解析】由抛物线的定义可知，422pPF ==+，所以4p =，所以抛物线的方程为28y x =，过点P 作PP '垂直抛物线的准线，垂足为P '，则426PM PF PM PP MP ''+=++= ，当且仅当P P '､和M 三点共线时等号成立，故选A.7.B 【解析】过点E 作EF AB ⊥，交AB 于点F ，在Rt ECD 中，因为30ECD ∠=，所以tan 18tan30DE CD DCE ∠==⨯= ，在Rt BEF 中，因为60BEF ∠= ，所以tan 15tan60BF EF FEB ∠==⨯= 则()36.4m AB BF AF BF ED =+=+=+=≈.故选B.8.D【解析】依题意圆C '是以AB 为直径的圆，当AB 最大时，圆C '的面积最大，因为11222AMC AB S MC AM AC =⋅⋅=⋅⋅ ，得2224||4441||MA AC MC AB MCMC MC -===-，又24MC ，当4MC =时，此时()0,0M 或(4,4)M ，AB 取最大值3C '的面积最大值为2π3)3π⋅=，故选D.二､多选题（本大题共3小题，每小题6分，共18分.）9.ABD 【解析】依题意函数()f x 的周期为2ππ2T ==，所以选项A 正确；因为()102f =，即1cos 2ϕ=，又π02ϕ-<<，所以π3ϕ=-，所以选项B 正确；因为()πcos 23f x x ⎛⎫=-⎪⎝⎭，又()5π5ππcos 2cos 2π1663f ⎛⎫⎛⎫⎛⎫-=⨯--=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以选项C 错误；因为ππ62x <<，所以π2π02π33x <-<<，所以函数()f x 在区间ππ,62⎛⎫⎪⎝⎭单调递减，所以选项D 正确，故选ABD.10.AC 【解析】()f x 为偶函数，()()f x f x ∴-=，又()g x 为奇函数，()()g x g x ∴-=-，()()2e x f x g x += ，①()()2e x f x g x -∴-+-=，即()()2e x f x g x --=，②由2+①②得：()e e x xf x -=+，所以选项A 正确；因为函数e ,e x x y y -==-在R 上均为增函数，故()e exxg x -=-在R 上单调递增，所以选项B 错误；因为()()2222e e e e 2x x x xf x --=+=+-，所以()()()2e e 2e e 2x xx x F x m --=+-+-，又()e e 2x x f x -=+ ，当e e x x -=，即0x =时等号成立，令[)e e 2,xxt ∞-=+∈+，设()22222()2h t t mt t m m =--=---，对称轴t m =，（1）当2m >时，函数()h t 在[)2,m 上为减函数，在(),m ∞+上为增函数，则()2min ()211h t h m m ==--=-，解得3m =或3m =-（舍）；（2）当2m 时，()h t 在[)2,∞+上单调递增，()min ()22411h t h m ==-=-，解得：1324m =>，不符合题意.综上3m =，所以选项C 正确，D 错误.故选AC .11.BCD【解析】对于选项A ，因为1AA ∥1CC ，又点P 与顶点1C 重合，所以1DC C ∠是异面直线1AA 与DP 所成角，其大小为45 ，故选项A 错误；对于选项B ，因为,M N 是侧棱11,BB CC 的中点，所以MN ∥11B C ，又点P 在线段MN 上，所以三棱锥11C PDB -的体积1111112221323C PDBD PC B V V --==⨯⨯⨯⨯=（定值），故B 正确；对于选项C ，因为点P 在线段1B C 上，连接111,,,AC AB BD B D ，因为1BB ⊥平面,ABCD AC ⊂平面ABCD ，则1BB AC ⊥，又因为ABCD 为正方形，则BD AC ⊥，且11,,BB BD B BB BD ⋂=⊂平面11BB D D ，则AC ⊥平面11BB D D ，且1BD ⊂平面11BB D D ，可得1AC BD ⊥，同理可得11AB BD ⊥，且11,,AC AB A AC AB ⋂=⊂平面1AB C ，则1BD ⊥平面1AB C ，因为AP ⊂平面1AB C ，所以1AP BD ⊥，故C 正确；对于选项D ，因为点P 为1BC 的中点，连接BD ，记AC 与BD 的交点为O ，取BC 的中点为F ，连接,PF OF ，则222OP OF PF =+=，又2OA OB OC ===，所以点O 为三棱锥P ABC -的外接球的圆心，所以三棱锥P ABC -的外接球的半径为2，所以三棱锥P ABC -的外接球的体积为342ππ2)33⨯=，故D 正确.故选BCD.三､填空题（本大题共3小题，每小题5分，共15分.）12.13【解析】由题意可得：()()()121133AM AB BM AB BC AB AC AB AC AB b c b c λλλλλλ=+=+=+-=+-=+-=+.所以13λ=.13.2325【解析】22ππππ123cos 2cos 2cos212sin 123366525αααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=-=-=--=-⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭.14.37,34⎣⎦【解析】因为12PF m PF =，由椭圆的定义可得()12212PF PF m PF a +=+=，所以2122,11a ma PF PF m m ==++.又因为1260F PF ∠=，由余弦定理可得：22222222cos6041111a ma a ma c m m m m ⎛⎫⎛⎫+-⋅= ⎪ ⎪++++⎝⎭⎝⎭.化简得22233111(1)2c m a m m m=-=-+++，又因为函数()12f m m m =++在区间[]2,3上单调递增，所以9116223m m ++ ，所以2217316c a .可得3734e ，所以椭圆C 的离心率取值范围为37,34⎣⎦.四､解答题（本大题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.）15.【解析】（1）由题意，设等差数列{}n a 的首项为1a ，公差为d ，又497,81a S ==，所以1137,98981,2a d a d +=⎧⎪⎨⨯+=⎪⎩解得11,2,a d =⎧⎨=⎩故()1121n a a n d n =+-=-.因为数列{}n b 为各项为正的递增数列，设公比为q ，且1q >，因为1238b b b =，所以3318b q =，得122b q b ==，又1237b b b ++=，所以2227q q++=，即()()2120q q --=，解得2q =，从而11b =，所以1112n n n b a q --==.（2）由（1）得()()1212,,212,,nn n n n c n n -⎧--⎪=⎨-⎪⎩为奇数为偶数所以()()212122124324122n n n n n c c n n ---+=--+-=，所以数列{}n c 的前2n 项和21234212n n nS c c c c c c -=++++++ ()()()2421234212222n n n c c c c c c -=++++++=+++ ()22221424143nn +--==-（或1443n +-）.16.【解析】（1）连接BE ，则12BC AD DE ==，因为AD ∥,BC AD DC ⊥，所以四边形BCDE 为矩形，所以2BE CD ==，因为PA PD ==，且E 为AD 的中点，所以PE AD ⊥，且2PE ==，所以22222228PE BE PB +=+==，即,PE BE ⊥又因为AD BE E ⋂=，所以PE ⊥平面ABCD ，又PE ⊂平面PAD ，所以平面PAD ⊥平面ABCD .（2）以E 为原点，EA 为x 轴，EB 为y 轴，EP 为z 轴建立如图所示的空间直角坐标系，则()()()()2,0,0,0,2,0,1,2,0,0,0,2A B M P -，设EN t =，则()0,0,N t ，所以()()2,2,0,2,0,2AB AP =-=- ，设平面PAB 的法向量为()111,,m x y z = ，则0,0,m AB m AP ⎧⋅=⎪⎨⋅=⎪⎩ 即1111220,220,x y x z -+=⎧⎨-+=⎩取()1,1,1,m = 又()()3,2,0,2,0,AM AN t =-=- ，设平面AMN 的法向量为()222,,n x y z = ，则0,0,n AM n AN ⎧⋅=⎪⎨⋅=⎪⎩ 即2222320,20,x y x tz -+=⎧⎨-+=⎩取3,,22t n t ⎛⎫= ⎪⎝⎭ ，所以323872|cos ,|||||29t t m n m n m n ++⋅〈〉==⋅ ，所以1t =，或10441t =（舍），线段EN 的长为1.17.【解析】（1）（i ）记i A 表示事件“第i 局公牛队获胜”，i B 表示事件“球员李明第i 局没有被罚出场”，1,2,3i =.由全概率公式公牛队每局比赛获胜的概率为()()()()023********i i i i i i P P B P A B P B P A B =+=⨯+⨯=∣∣.（ii ）由已知随机变量X 的可能取值为2，3.()2222521339P X ⎛⎫⎛⎫==+-= ⎪ ⎪⎝⎭⎝⎭，()112222222243C 1C 113333339P X ⎛⎫⎛⎫⎛⎫==⋅⋅-⋅+⋅⋅-⋅-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，随机变量X 的分布列如下表：X23P 5949()542223999E X =⨯+⨯=.（2）依题意事件A 擂王公牛队2:0获得挑战赛胜利的可能情形是：两局比赛李明均没有被罚出场；第一局李明没有被罚出场，第二局被罚出场；第一局李明被罚出场，第二局不能参加比赛.所以()()()2331111144222P A p p p p ⎡⎤=-⋅+-⋅⋅⋅+⋅⋅⎢⎥⎣⎦2141131633p ⎡⎤⎛⎫=-+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.又11,62p ⎡⎤∈⎢⎥⎣⎦，则当12p =时()min 2364P A =.即事件A 的概率的最小值为2364.18.【解析】（1）因为124PF PF -=，所以24a =，得2a =，又三角形12PF F120012F F y ⋅==0y =，得P ⎛⎫ ⎝代入双曲线方程得2225414b b +-=，得221,5b b ==-（舍），所以双曲线E 的方程为：2214x y -=.（2）由题意，()1,0M ，且12,l l 斜率存在且不为0，设()()()()112233441122,,,,,,,,:1,:1A x y B x y C x y D x y l x m y l x m y =+=+，由几何性质可知122,2m m >>，联立方程221440,1,x y x m y ⎧--=⎨=+⎩得()22114230m y m y -+-=，Δ0>恒成立，11212221123,44m y y y y m m --+==--，同理可得：23434222223,44m y y y y m m --+==--，直线AC 方程：()311131y y y y x x x x --=--，令1x =，得()()211331311111131231123111G m m y y y y y y y y x y m y x x m y m y m y m y ---=+-=-=---，同理：()21242412H m m y y y m y m y -=-，因为()()2113212423112412G H m m y y m m y y y y m y m y m y m y --+=+--()()()()()1324122423112123112412y y m y m y y y m y m y m m m y m y m y m y -+-=---()()()()()23412112342123112412m y y y y m y y y y m m m y m y m y m y +-+=---()()()2112222221122123112412323244440m m m m m m m m m m m y m y m y m y ----⋅-⋅----=-=--，所以G H y y =-，所以1GHMGy MH y ==.19.【解析】（1）因为()e 3x f x x =-，所以()e 3x f x '=-，当ln3x <时，()0f x '<，函数()f x 单调递减；当ln3x >时，()0f x '>，函数()f x 单调递增，所以()()()ln3min ln3e3ln331ln30f x f ==-=-<，又()()020e 10,2e 60f f ==>=->，所以()f x 有两个不同零点.（2）当1a =时，()e 3xf x x =-，由()cos 2f x x x - ，得e cos x x x - ，令()e x h x x =-，则()e 1xh x '=-，当0x <时，()()0,h x h x '<在(),0∞-上为减函数，当0x >时，()()0,h x h x '>在()0,∞+上为增函数，所以()()01h x h = ，而cos 1x ，且()0cos0h =，所以e cos x x x - ，即()cos 2f x x x - .（3）由已知()12sin f x x - ，即2e 32sin 10x a ax x -+- ，因为[)1,a ∞∈+，令()2e 32sin 1x g a a xa x =-+-为开口向上的二次函数，对称轴为32e xx a =，令()32e x x x ϕ=，所以()()312ex x x ϕ-='，当1x <时，()0x ϕ'>，函数()x ϕ单调递增；当1x >时，()0x ϕ'<，函数()x ϕ单调递减，所以()()max 3112e x ϕϕ==<，即3312e 2ex x a =< ，故()g a 在区间[)1,∞+上单调递增，所以()()1e 32sin 1x g a g x x =-+- ，从而只需证明e 32sin 10x x x -+- 即可，即证32sin 110e xx x -+- ，令()32sin 11e x x x F x -+=-，则()232sin 2cos e x x x x F x '-+-=，令()232sin 2cos q x x x x =-+-，则()π32cos 2sin 304q x x x x '⎛⎫=-++=+-< ⎪⎝⎭，所以函数()q x 单调递减，且()00q =，所以当0x <时，()0F x '>，当0x >时，()0F x '<，所以函数()F x 在(),0∞-上单调递增，在()0,∞+上单调递减，故()()00F x F = ，即32sin 110e x x x -+- ，。

湖南省教育厅关于进一步加强普通高等学校教学工作提高教学质量的若干意见文章属性•【制定机关】湖南省教育厅•【公布日期】2005.11.10•【字号】湘教发[2005]113号•【施行日期】2005.11.10•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】中等教育正文湖南省教育厅关于进一步加强普通高等学校教学工作提高教学质量的若干意见（湘教发[2005]113号）根据教育部《关于进一步加强高等学校本科教学工作的若干意见》（教高[2005]1号），结合我省实际，现就全省普通高等学校今后一个时期进一步加强教学工作，全面提高教学质量，提出如下意见：一、进一步强化教学质量意识1、高校要坚持和落实以人为本的科学发展观，牢固树立人才培养是学校的根本任务、教学质量是学校生存和发展的生命线的意识，牢固确立教学工作在学校各项工作中的中心地位、教学改革的核心地位和教学投入的优先地位；正确处理发展规模与办学质量、效益之间的关系，教学与科研、社会服务之间的关系，教学工作与学校其他工作之间的关系；进一步加强教学工作，构建具有先进教学理念、现代课程体系、科学培养模式和完善的质量保障制度的有效的教学运行机制，着力提高大学生的学习能力、实践能力和创新能力。

2、强化教学质量意识，建立健全教学工作责任制。

高校的党政一把手要做名副其实的教学质量第一责任人，深入教学第一线，亲自抓教学质量，不断推进学校的教学观念创新、制度创新和工作创新，把质量意识落实到各项工作中。

学校各职能部门要进一步增强为教学服务的意识，围绕提高教学质量、培养高素质人才这一根本任务，主动地、创造性地为教学工作服务。

学校要建立定期研究教学工作的制度，每学期召开两次以上党政领导联席会议，专题研究教学工作。

要明确各职能部门和各级教学单位的职能职责，把保证教学质量的责任分解落实到各职能部门、各级教学单位和各项工作中。

二、切实加强教学基本条件建设3、高校要调整经费支出结构，切实加大教学投入。

湖南省2023年普通高等学校对口招生考试数学本试题卷包括选择题、填空题和解答题三部分，共5页。

时量120分钟。

满分120分。

一、选择题(本大题共10小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的)1.已知集合A={1,2,3},B={2,3,4},则A⋃B=A.{1,4}B.{2,3}C.{2,3,4}D.{1,2,3,4}2.不等式x²-2x-3≤0的解集是A.[-1,3]B.[-3,1]C.(-∞,-1)⋃[3,+∞)D.(-∞,-3)⋃[1,+∞)3.已知直线l1:y=2x+1与直线l2:x+ay=0.若l1//l2,则a的值为A.-2B.C. D.24.已知奇函数f(x)在[-3,0]上是减函数，且f(-3)=2,则f(x)在[0,3]上的最小值为A.-3B.-2C.0D.35.已知圆锥的底面圆半径为1,侧面积为2π,则该圆锥的体积为A. B.πC.3πD.23π数学试题第1页(共5页)6.已知向量a=(1,2),b=(3,2),则与向量2a-b平行的向量可以是A.(2,-1)B.(1,-2)C.(-2,-1)D.(-1,-2)7.已知函数f(x)=a²(a>0,且a≠1)满足,则不等式f(x)≥8的解集是A.(-∞,-3)B.C.(3,+∞)D.8.从某小学随机抽取100名学生，将他们的身高数据绘成频率分布直方图如下图所示.若从身高在(120,130),(130,140),[140,150]三组内的学生中，用分层抽样的方法抽取18人参加一项活动，则从身高在[140,150]内的学生中抽取的人数为A.9B.6C.4D.39.已知函数f(x)=|lgx|,),b=f(3),,则a,b,c的大小关系是A.c<a<bB.a<c<bC.c<b<aD.a<b<c10.下列命题中正确的是A.函数y=2sinx的周期为πB.函数y=sinx在区间内是减函数C.函数y=sinx的图像与函数y=cosx+3的图像有交点D.函数y=cosx的图像可由的图像向左平移个单位得到二、填空题(本大题共5小题，每小题4分，共20分)11.已知,则12.已知函数若f(a)=-4,则a=·13.某乒乓球队有5名队员，需派3名参加比赛.教练计划从2名主力队员中选1名排在第二场的位置，从其余3名非主力队员中选2名排在第一、三场位置，那么共有种不同的出场安排(用数字作答).14.已知直线I:y=x+2与圆C:x²+y²-2y=0交于A,B两点，则|AB|=15.设等差数列{an }的前n项和为Sn.若S10=20,a2+a4+a6+a8+a10=15,则Sn的最小值为·三、解答题(本大题共7小题，其中第21,22小题为选做题.满分60分，解答应写出文字说明、证明过程或演算步骤)16.(本小题满分10分)已知函数f(x)=log₂(1+x),g(x)=log₂(1-x).(1)判断函数h(x)=f(x)-g(x)的奇偶性，并说明理由；(2)求方程f(x)=g(x)+1的解.17.(本小题满分10分)已知等比数列{an }的公比q≠1,a1=1,且a1,a3,a2成等差数列.(1)求{an}的通项公式；(2)设|,求数列{bn }的前n项和Sn.18.(本小题满分10分)为推进地区教育均衡发展，某市教育局拟从6名优秀教师中抽取人员分三批次赴农村薄弱学校进行支教，每批次需从6名教师中随机抽取2名教师支教，且每批次抽取互不影响.(1)求在这3批次支教活动中教师甲恰有2次被抽中的概率；(2)已知这6名教师中有2名数学教师，设第一批次抽到的数学教师人数为ξ,求ξ的分布列.19.(本小题满分10分)如图，在三棱锥A-BCD中，AC⊥BD.平面α交AB,BC,CD,DA分别于E,F,G,H,且AC//平面α,BD//平面α.(1)证明：四边形EFGH为矩形；(2)若AC=BD=2,求矩形EFGH面积的最大值.(第19题图)20.(本小题满分10分)已知抛物线C:x²=2py(p>0)的焦点为F(0,1),过点F的直线1交C于A,B两点.(1)求抛物线C的标准方程及其准线方程；(2)设E为C的准线与y轴的交点，直线AE,BE的斜率分别为k1,k2,证明：k₁+k₂=0.选做题：请考生在第21,22题中选择一题作答.如果两题都做，则按所做的第21题计分.作答时，请写清题号.21.(本小题满分10分)如图，已知在△ABC中，AB=3,BC=4.(1)若∠ABC=60°,求AC的长；(2)若D为AC的中点，求的值.(第21题图)22.(本小题满分10分)某客运公司用A,B两种型号的车辆承担甲地至乙地的长途客运业务，每车每天出车一次，A,B两种型号的车辆的载客量分别为30人和50人，营运成本分别为1200元/辆和2400元/辆，公司拟组建一个不超过28辆车的客运车队，并要求B型车不多于A型车8辆.如果要求每天运送从甲地去乙地的旅客不少于1000人，那么公司应配备A型车、B型车各多少辆，才能使得公司的营运成本最低，最低是多少元?湖南省2023年普通高等学校对口招生考试数学参考答案一、选择题1.D 2.A 3.B 4.B 5.A 6.B 7.C 8.D 9.C 10.D二、填空题11.012.-113.1214.215.-16三、解答题16(1)为奇函数。

湖南省教育厅关于印发《湖南省2024年普通高等学校艺术类专业招生工作实施办法》的通知文章属性•【制定机关】湖南省教育厅•【公布日期】2023.12.14•【字号】湘教发〔2023〕48号•【施行日期】2023.12.14•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】高等教育正文湖南省教育厅关于印发《湖南省2024年普通高等学校艺术类专业招生工作实施办法》的通知湘教发〔2023〕48号各市州教育（体）局、各艺术类专业在湘招生普通高校：根据《教育部办公厅关于做好2024年普通高等学校部分特殊类型招生工作的通知》（教学厅〔2023〕10号）和我省普通高校艺术类专业招生有关政策规定，我厅制定了《湖南省2024年普通高等学校艺术类专业招生工作实施办法》（简称《实施办法》）。

现将教育部教学厅〔2023〕10号文件和我省《实施办法》一并印发给你们，请认真贯彻执行。

请各市州教育（体）局及时将本通知转发至辖区内教育行政部门、招生考试机构和各高中阶段学校，严格按照属地原则做好政策解读和监督管理等工作。

湖南省教育厅2023年12月14日湖南省2024年普通高等学校艺术类专业招生工作实施办法为做好我省2024年普通高校艺术类专业招生工作，根据教育部普通高校艺术类专业招生有关政策规定，结合我省工作实际，制定本办法。

一、招生专业范围1.艺术类专业是指2023年《普通高等学校本科专业目录》中“艺术学”门类下设各专业，以及《职业教育专业目录（2021年）》中高等职业教育本科和专科专业“艺术设计类”“表演艺术类”下设各专业和“民族文化艺术类”“广播影视类”等部分专业。

2.艺术类专业分为两类：一类是不组织专业考试的专业，包括艺术史论、艺术管理、非物质文化遗产保护、戏剧学、电影学、戏剧影视文学、广播电视编导、影视技术等（专科专业参照执行）；一类是可组织专业考试的专业，包括音乐类、舞蹈类、表（导）演类、播音与主持类、美术与设计类、书法类、戏曲类等，有关高校也可根据人才培养实际不对考生专业考试成绩提出要求，原则上高校同一艺术类专业应对应一个省级统考科类要求，且在各招生省份保持一致。

湖南省教育厅关于印发《湖南省2023年普通高等学校招生工作实施办法》的通知文章属性•【制定机关】湖南省教育厅•【公布日期】2023.05.10•【字号】湘教发〔2023〕14号•【施行日期】2023.05.10•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】高等教育正文湖南省教育厅关于印发《湖南省2023年普通高等学校招生工作实施办法》的通知湘教发〔2023〕14号各市州教育（体）局、普通高等学校：根据《教育部关于做好2023年普通高校招生工作的通知》（教学〔2023〕1号）等文件规定，结合我省实际，我厅制定了《湖南省2023年普通高等学校招生工作实施办法》。

现印发给你们，请认真贯彻落实。

湖南省教育厅2023年5月10日湖南省2023年普通高等学校招生工作实施办法为做好我省2023年普通高校考试招生工作，保障高校选拔符合培养要求的新生，依据教育部和我省相关规定，制定本实施办法。

高校招生工作应贯彻公平竞争、公正选拔、公开透明的原则，德智体美劳全面考核、综合评价、择优录取新生。

一、报名1.我省2023年高考报名按《教育部关于做好2023年普通高校招生工作的通知》（教学〔2023〕1号）和《湖南省人民政府办公厅转发省教育厅等部门〈关于做好进城务工人员随迁子女接受义务教育后在当地参加升学考试工作实施办法〉的通知》（湘政办发〔2012〕115号）相关规定执行。

考生报名后，经资格审核，对不符合报考条件的考生，将取消其高考报名资格，已录取的取消其录取资格。

具体报名条件、时间和办法等由各级招生考试机构按湖南省教育考试院《关于做好2023年普通高等学校招生考试报名工作的通知》（湘教考普字〔2022〕14号）要求实施。

二、考试2.我省普通高校招生考试采用“3+1+2”模式，考试科目由全国统考科目（简称统考科目）和普通高中学业水平选考科目（简称选考科目）组成。

其中，“3”为语文、数学、外语（含英语、俄语、日语、法语、德语、西班牙语）3门统考科目，由全国统一命题。