当前位置：文档之家 › 759线性系统理论Linear System Theory

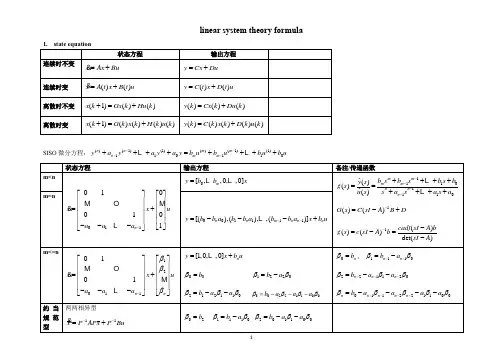
759线性系统理论Linear System Theory

  • 格式：ppt
  • 大小：96.50 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

线性系统理论公式

线性系统理论公式
能控规范型
能测规范型
n维完全
，
，
旺纳姆
龙伯格
连续时不变结构分解
4.稳定性
连续时间
强条件
弱条件
内->外部稳定
渐进稳定： 系数必须同号才有负实部
BIBO稳定： a(s)同号负实部
大范围渐进稳定
所有非零状态 正定
负定
时，有 ，则平衡状态
所有非零状态 正定
负半定
对任意非零
时，有 ，则平衡状态
小范围渐进稳定
所有非零状态 满足 正定
1.定义法：
2.两两相异：
3.预测举证：
连续时间时不变
连续时间时变
离散时不变
离散时变
3.能控性与能测性
格拉姆矩阵
秩判据
PBH
约当规范型
连续时不变全能控
非奇异
行满秩
不含0行
连续时不变全能测
非奇异
列满秩
不含0列
连续时变全能控
， ，
连续时变全能测
， ，
离散时不变能控
与G非奇异
G非奇异，
离散时不变能测
非奇异
问题：主要求配置特征值
1.
实部相距4～6人倍原则，
2. ,解出
状态反馈阵K1和K2，使闭环特征值配置为λ1、λ2
K1:在不完全能控下
1.设计 ， ，完成全能控
2.
3.
4.
5.
极点配置
反馈(完全能控)
观测(完全能测)
求k
能控规范：
负定
则平衡状态 在
所有非零状态 满足 正定
负半定
对任意非零
则平衡状态 在
不稳定
足 正定， 正定

线性系统理论

线性系统理论

Linear Systems Theory: A Structural Decomposition Approach线性系统理论: 结构分解法Ben M. Chen （陈本美）新加坡国立大学Zongli Lin（林宗利）美国弗吉尼亚大学Yacov Shamash (雅科夫 司马诩)美国纽约州立大学石溪分校此书献给我们的家人前两位作者谨以这中译版献给他们的母校 厦门大学目录绪论1 导论和预览1.1 背景1.2 各章预览1.3 符号和术语2 数学基础2.1 导论2.2 矢量空间和子空间2.3 矩阵代数和特性2.3.1 行列式、逆和求导2.3.2 秩、特征值和约当型2.3.3 特殊矩阵2.3.4 奇异值分解2.4 范数2.4.1 矢量范数2.4.2矩阵范数2.4.3 连续时间信号范数2.4.4 离散时间信号范数2.4.5 连续时间系统范数2.4.6 离散时间系统范数3 线性系统理论复习3.1 导论3.2 动态响应3.3 系统稳定性3.4 可控性和可观性3.5 系统可逆性3.6 常态秩、有限零点和无限零点3.7 几何子空间3.8 状态反馈和输出馈入的特性3.9 练习4 无驱动和/或无检测系统的分解4.1 导论4.2 自治系统4.3 无驱动系统4.4 无检测系统4.5 练习5. 正则系统的分解5.1 导论5.2 SISO系统5.3 严格正则系统5.4 非严格正则系统5.5 结构化分解特性的证明5.6 系统矩阵的Kronecker型和Smith型5.7 离散时间系统5.8 练习6 奇异系统的分解6.1 导论6.2 SISO奇异系统6.3 MIMO描述系统6.4 定理6.3.1的证明和性质6.5 离散时间奇异系统6.6 练习7 双线性变换的结构化映射7.1 导论7.2 连续到离散时间系统的映射7.3 离散时间到连续时间系统的映射7.4 定理7.2.1的证明7.5 练习8 系统因子分解8.1 导论8.2 严格正则系统8.3 非严格正则系统8.4 离散时间系统8.5 练习9 通过选择传感器/执行器实现的结构配置9.1 导论9.2 同时有限和无限零点结构配置9.2.1 SISO系统9.2.2 MIMO系统9.3 完全结构配置9.4 练习10 通过状态反馈实现的时间尺度和特征结构配置10.1 导论10.2 连续时间系统10.2.1 设计步骤和基本特性10.2.2 控制、控制和干扰解耦10.3 离散时间系统10.3.1设计步骤和基本特性10.3.2 控制、控制和干扰解耦10.4 练习11 通过静态输出反馈实现的干扰解耦11.1 导论11.2 左可逆系统11.3 一般的多变量系统11.4 练习12 软件工具箱12.1 导论12.2 m-函数描述12.2.1 自治系统的分解12.2.2 无驱动和无检测系统的分解12.2.3 正则系统的分解和特性12.2.4 矢量空间的运算12.2.5 奇异系统的分解和特性12.2.6 系统分解12.2.7 通过选择传感器/执行器实现结构配置12.2.8 具有特征结构配置的状态反馈控制12.2.9 通过静态输出反馈实现干扰解耦参考文献索引前言系统的结构特性对我们理解以状态空间表示的线性系统起着重要作用。

线性系统理论第一章

线性系统理论第一章

Introduction


Course website: Interactive Teaching Space on UESTC website. Lecture notes and notice will be put on the website.
Hale Waihona Puke Introduction
Prerequisite:


Linear algebra Signal and System Working Knowledge of Matlab programming
Introduction

Textbook:


Reference books:

C. Chen, Linear System Theory and Design, Oxford University Press, 1999.
Linear System Theory
Introduction

Motivation

This course presents basic knowledge of linear system by teaching: Mathematical modeling of systems Solutions of linear dynamic equation and impulse response, and realization of linear system Characteristics of linear systems: controllability, observability, and stability Design of linear control system and pole placement Linear Optimal Control and Robust Control

线性系统理论学习指南

线性系统理论学习指南

线性系统理论学习指南英文回答：Linear system theory is a fundamental topic in thefield of control engineering. It provides a mathematical framework for analyzing and designing systems that can be described by linear equations. In this learning guide, I will explain the key concepts and techniques in linear system theory.Firstly, let's start with the definition of a linear system. A linear system is a mathematical model that can be represented by a set of linear equations. These equations describe the relationship between the inputs and outputs of the system. The behavior of a linear system can be analyzed using techniques such as transfer functions, state-space representations, and frequency domain analysis.One important concept in linear system theory is the transfer function. The transfer function is a mathematicalrepresentation of the input-output relationship of a linear system. It is defined as the ratio of the Laplace transform of the output to the Laplace transform of the input, assuming all initial conditions are zero. The transfer function provides valuable information about the system's stability, dynamics, and frequency response.To illustrate this, let's consider an example of a simple linear system. Imagine a spring-mass-damper system, where a mass is attached to a spring and a damper. Theinput to the system is the force applied to the mass, andthe output is the displacement of the mass. By applying Newton's second law and solving the resulting differential equation, we can derive the transfer function of the system. This transfer function will tell us how the displacement of the mass is related to the applied force.Another important concept in linear system theory isthe state-space representation. The state-space representation provides a more comprehensive description of a linear system by considering both the inputs and outputs as well as the internal states of the system. It consistsof a set of first-order differential equations that describe the evolution of the system's states over time. The state-space representation is particularly useful for analyzing the system's controllability, observability, and stability.To further illustrate this, let's consider a control system that aims to regulate the temperature of a room. The inputs to the system are the heater power and the outside temperature, and the output is the room temperature. By formulating the system dynamics and the output equation in state-space form, we can analyze the controllability of the system and design a suitable controller to achieve the desired temperature regulation.In addition to transfer functions and state-space representations, frequency domain analysis is another important tool in linear system theory. Frequency domain analysis allows us to study the system's behavior in the frequency domain, which is particularly useful for analyzing the system's stability and frequency response. Techniques such as Bode plots, Nyquist plots, and rootlocus plots are commonly used in frequency domain analysis.To illustrate this, let's consider a feedback control system that aims to stabilize an unstable plant. By analyzing the system's transfer function in the frequency domain using Bode plots, we can determine the stability margins and design a suitable controller to stabilize the system.中文回答：线性系统理论是控制工程领域的基础知识。

线性系统理论第三章

线性系统理论第三章

为约旦标准型
J1 0
A
P 1AP
0
J2
0 A PAP 1
0
0
0
J
n
i 1
Ji
0
i
0
0
0
1
i nini
, eJit
如何计算矩阵指数函数 eAt ？
§3.2 矩阵指数函数的计算
Linear system theory
1. 拉普拉斯变换方法：
eAt I
At
1
A2t 2
2!
两边取拉普拉斯变换，有
1 Ak t k
k0 k !
L
e At
L
I
At
1 2!
A2t
2
1 s
I
1 s2
A
1 s3
A2
另外一方面，有
exp[(M 1AM )t] M 1eAt M = exp[(M 1AM )t]
(M 1AM )k t k
M 1 Ak M t k
M 1(
Ak t k )M = M 1eAt M
k 0
k ! k0
k!
k0 k !
§3.1 状态方程的解
Linear system theory
3. 强迫运动： 当 u(t) 0，给定
t2 )
A2
(
t12 2!
t1t2
t22 ) 2!
A3 (t13 3!
t12t2 2!
t1t22 2!
t23 ) 3!
Ak ( t1k
t1k 1t2
t1k
t2 2 2
k ! (k 1)! (k 2)!
t12t2k2 t1t2k2 t2k ) = e A(t1t2 ) 2!(k 2)! (k 1)! k !

线性系统理论

线性系统理论

线性系统理论线性系统理论是一个广泛应用的数学分支，该分支研究线性系统的性质、行为和解决方案。

线性系统可以描述很多现实世界中的问题，包括电子、机械、化学和经济系统等。

在这篇文章中，我们将探讨线性系统理论的基础、应用、稳定性和控制等不同方面。

一、线性系统基础线性系统是一种对于输入响应线性的系统。

当输入为零时，系统的响应为零，称之为零输入响应。

当没有外界干扰时，系统内部存在固有的动态响应，称之为自然响应。

当有外界输入时，系统将对输入做出响应，称之为强制响应。

线性系统具有很多性质，可以让我们更好地理解系统的行为。

其中一个重要的性质是线性可加性，就是说当输入是线性可加的时候，输出也是线性可加的。

换句话说，如果我们有两个输入信号，将它们分别输入到系统中，我们可以在系统的输出中将它们加起来，并得到对应的输出信号。

另外一个重要的性质是时不变性，就是说当输入信号的时间变化时，输出信号的时间变化也会随之发生。

这个性质告诉我们，系统的行为不随着时间的改变而改变。

除此之外，线性系统还有其他很多性质，比如可逆性、稳定性、因果性等等。

二、线性系统的应用线性系统有着广泛的应用，它们可以用来描述很多各种各样的问题，包括但不限于电子电路、航天控制、化学反应、经济系统等等。

下面我们来看看这些应用领域中的具体案例。

1. 电子电路线性系统在电子电路中有着广泛应用。

例如，如果我们想要设计一个低通滤波器，以使高频信号被抑制，我们可以使用线性系统来描述它的行为。

我们可以将电子电路看作一个输入信号到输出信号的转换器。

这个转换器的输出信号可以通过控制电子器件的电流、电压等参数来实现。

这种线性系统可以用来滤掉任何频率的信号，因此在广播和通信中也有广泛的应用。

2. 航天控制航天控制是线性系统理论的一个应用重点。

它包括控制飞行器姿态、轨道以及动力学行为。

在这些问题中，线性可变系统被广泛应用。

这种系统的输出信号是受到飞行器的控制和环境因素的影响。

控制器的任务是计算信号，以引导飞行员和总体系统实现期望的性能和特征。

线性系统理论全PPT课件

线性系统理论全PPT课件
详细描述
稳定性是线性系统的一个重要性质，它决定了系统在受到外部干扰后能否恢复到原始状态。如果一个系统是稳定 的，那么当外部干扰消失后，系统将逐渐恢复到原始状态。而不稳定的系统则会持续偏离原始状态。
03
线性系统的数学描述
状态空间模型
01
定义
状态空间模型是一种描述线性动态系统的方法，它通过状态变量和输入
航空航天控制系统的线性化分析
线性化分析
在航空航天控制系统中，由于非线性特性较强，通常需要进行线性化分析以简化系统模 型。通过线性化分析，可以近似描述系统的动态行为，为控制系统设计提供基础。
线性化方法
常用的线性化方法包括泰勒级数展开、状态空间平均法和庞德里亚金方法等。这些方法 可以将非线性系统转化为线性系统，以便于应用线性系统理论进行控制设计。
线性系统理论全ppt课件
• 线性系统理论概述 • 线性系统的基本性质 • 线性系统的数学描述 • 线性系统的分析方法 • 线性系统的设计方法 • 线性系统的应用实例
01
线性系统理论概述
定义与特点
定义
线性系统理论是研究线性系统的 数学分支，主要研究线性系统的 动态行为和性能。
特点
线性系统具有叠加性、时不变性 和因果性等特性，这些特性使得 线性系统理论在控制工程、信号 处理等领域具有广泛的应用。
线性系统的动态性能分析
动态性能指标
描述线性系统动态特性的性能指 标，如超调量、调节时间、振荡
频率等。
状态空间分析法
通过建立和解决线性系统的状态方 程来分析系统的动态性能，可以得 到系统的状态轨迹和响应曲线。
频率域分析法
通过分析线性系统的频率特性来描 述系统的动态性能，可以得到系统 的频率响应曲线和稳定性边界。

线性系统理论 西工大

线性系统理论 西工大

线性系统理论
第一章 线性系统的状态空间描述
为了分析研究系统，建立描述系统的数学方程是首要 的。经典控制理论中的时间域理论对单输入-单输出线性 定常系统用高阶微分方程或传递函数来描述输入-输出变 量间的因果关系，分析的主要方面限于运动的稳定性，不 便用来综合系统。 20世纪60年代以后，现代线性系统理 论又有了新发展，出现了线性系统几何理论、线性系统代 数理论和多变量频域方法等研究多变量系统的新理论和新 方法。
x1 x xn
y1 y yq
（1.10）
分别为状态向量、控制向量（输入向量）、输出向量。
线性系统理论
1.1 系统的状态空间描述
再引入向量函数
f1 ( x , u, t ) f ( x , u, t ) f n ( x , u, t )
线性系统理论
随着计算机技术的发展，以线性系统为对象的计算方法 和计算辅助设计问题也受到普遍的重视。运用状态空间法 研究系统是现代控制理论的重要标志，状态空间方程是现
代控制理论的最基本的数学模型。本章主要介绍状态空间
描述的基本概念以及建立状态空间方程的方法。
线性系统理论
§1.1
§1.2 §1.3 §1.4 §1.5
松弛性
系统在时刻 t 0 称为松弛的，当且仅当输出 y[t0 , )由输 入 u[t0 , )唯一确定。从能量的观点看，在时刻 t 0不存在存 储能量，则称系统在时刻 t 0 是松弛的。式中 u[t0 , )表示定 义在时间区间[t0 , ) 的输入。
线性系统理论
例如一个RLC网络，若所有电容两端的电压和流过电 感的电流在 t 0 时刻均为零（即初始条件为零），则网络称 为在 t 0 时刻是松弛的。若网络不是松弛的，其输出响应

线性系统理论

线性系统理论

自主控制系统的应用迅速增长
The use of autonomous systems is rapidly increasing
居家自动化
CD播放器控制
•激光头定位控制 •驱动器速度控制
过程控制
电力控制
制造自动化
汽车自动控制
自适应巡行控制
智能车辆高速公路系统
空中交通控制
未来空战系统
集成控制技术 资源共享 因特网 信息集成 信息技术 控制技术 网络控制技术
工厂自动化 计算机集成制造系统（CIMS） 计算机集成过程系统（CIPS）
三、现代控制理论发展的主要标志
卡尔曼：
状态空间法 卡尔曼： 能控性与能观性 庞特里雅金：极大值原理
学出版社, 2002 Kailath T. Linear Systems. Prentice-Hall, 1980
九、作业与成绩
通常，每两周布置一次作业
最终考试成绩占总成绩的70％ 平时成绩占总成绩的30％

现代控制理论诞生
目前状况
控制已经成为一个具有坚实理论基础和广泛
应用的领域. 几乎所有实用的控制器是由数字计算机实现 的.
教育: 自动控制课程象野火般迅速传播，已经 成为工程师教育的重要组成部分. 应用: 控制概念已经很好地应用于很多领域.
应用
Full automatic flight
including take off and landing is a development that naturally follows autopilots. Autonomous flight is a challenging problem because it requires automatic handling of a wide variety of tasks--hybrid control New York Times, 1947

线性系统理论课件--Linear System Theory and Design(Part5)

线性系统理论课件--Linear System Theory and Design(Part5)
n n −1 D (λ1 ) = λ1 + α1λ1 + L + α n −1λ1 + α n = 0
(7.12) Then (7.11)
Let us define v := [λ can be written as
n −1 1
L λ1 1 ≠ 0 .
]
T
N (λ1 ) = cv = [β1
β 2 L β n ]v = 0
Let us introduce a new variable v(t) defined by
ˆ( s ) = D −1 ( s )u ˆ ( s) v
or
ˆ( s ) = u ˆ(s) D ( s )v
ˆ ( s ) = N ( s )v ˆ( s ) y
(7.3) (7.4)
Define state variables as
Definition 7.3’: Two polynomial are said to be coprime if they have no common factor of degree at least 1, or their gcd R(s) is a nonzero constant.
Theorem 7.1 The controllable canonical form (7.9) is observable if and only if D(s) and N(s) are coprime.
ˆ1 ( s ) = −α1 x ˆ1 ( s ) − L − α n −1 x ˆn −1 ( s ) − α n x ˆn ( s) + u ˆ ( s) sx
In the time domain, it is & 1 (t ) = [− α1 L − α n −1 − α n ]x(t ) + 1 ⋅ u (t ) x Substituting (7.5) into (7.4) yields

线性系统理论

线性系统理论
线性系统理论
王晶 信息学院自动化系 jwang@
参考教材



线性系统理论，郑大钟，清华大学出版社 Linear System Theory and Design, ChiTsong Chen, Oxford University Press 线性系统理论，段广仁，哈尔滨工业大学 出版社 线性系统理论和设计，仝茂达 ，中国科 大出版社
洪奕光，程代展，《非线性系统的分析与控制 》




代数理论：抽象化、形式化、符号化。用抽象
代数工具来研究线性系统，特点就是把系统各变量 之间的关系看作某些代数结构之间的映射关系，从 而把线性系统的分析，描述完全的形式化，抽象化， 变成纯粹的代数问题。 起源：60年代，Kalman运用模论工具对域上线性系 统的研究，随后在比域更弱的代数系上，如环、群、 泛代数、集合上建立了线性系统代数理论。 R.E.Kalman， P.L.Falb and M.A.Arbib， Topics in Mathematical System Theory，McGraw-Hill，1969





多变量频域方法，实质是以状态空间为基础，采 用频率域的系统描述和计算方法，只适用于定常系 统。分类：频率域设计方法（MIMO－SISO，推广 经典频域理论）和多项式矩阵理论（采用传递函数 矩阵的矩阵分式描述，基于多项式矩阵的计算与变 换）。 H.H.Rosenbrock， State Space and Multivariable Theory, Nelson, London,1970. A.G.J.MacFarlane ed., Complex Variable Methods for Linear Multivariable Feedback Systems, Taylorand Francis Ltd., 1980

线性系统理论第二章

线性系统理论第二章

y4 kx4 2kx2 2 y2 y3 kx3 k ( x1 x2 ) y1 y2 y2 kx2 y1 kx1 x1
x4 2 x2 x 2 x3 x1 x2 x
Physical System Validate
Verify Model Control
Analyze
Verification
Model Performance acceptible Update model/analysis Analyze Control
Simulate
Simulation / Visualization
Milestones in development of Control Theory

Classical Control Theory:




Before 1950’s. Characterized by Transfer Function analysis method. Not very good for multi-variable or large-scale system Root Locus, Frequency Response methods are extensively used Very much dependent on design experience
Input System Output

Why we need to study a system?

Because we want to control it.
What is control?

Roughly speaking, control is to make a system behave like we desire.

线性系统理论(xue)

线性系统理论(xue)

线性系统理论Linear System Theory 1-1 状态空间的基本概念例1-1 图示RLC 网络。

设：u i 为输入变量；u o =u c 为输出变量。

2 状态空间描述中常用的基本概念例1-1 图示RLC 网络。

设：u i 为输入变量；u o =u c 为输出变量。

用矩阵表示状态空间表达式：⎪⎨+−−=u x R x x 11&1-2 线性连续系统状态空间表达式的建立1......)((b s b s b s b s Y G n n ++++−1 N(s)/D(s)的串联分解——可控标准型实现x&x x⎤⎡⎡00010L &状态变量图例1-5 已知系统微分方程：u u T y y y +=ω+ωζ+试求系统的状态空间表达式，并绘制该系统的状态变量图。

21u x x x+ζω−ω−=22&2 可观测标准型实现设可控标准型实现为例1-6 已知系统微分方程：试求可观测标准型实现，并绘制其状态变量图。

3 并联分解——Jordan标准型实现⎤⎡−s L 0001ss s s U s G 89)()(23++==例1-7 已知某系统传递函数:⎡1⎤4 矩阵的特征方程、特征值1）方阵2 线性定常连续系统状态方程的求解2-1 齐次状态方程的解⎢⎣⎥⎦⎢⎣−−=⎥⎦⎢⎣22x 32x &解：用拉氏变换的方法:例2-1 求已知状态方程的状态转移矩阵。

2-2 状态转移矩阵的性质例2-2 已知状态转移矩阵，求Φ-1和系统矩阵A。

性质9 若例2-3已知系统矩阵，求状态转移矩阵及其状态转移矩阵的逆。

非齐次状态方程：例2-4 已知状态空间描述及零初始条件，输入为单位阶跃，求状态方程的解SISO系统：例9-29 已知系统动态方程，试求系统的传递矩阵。

⎡x&9-4-2开环与闭环传递矩阵MIMOU(s)E(s)Y(s)由图可知：3-1 线性系统的可控性与可观性3-1-1 问题的提出例3-2 已知系统状态空间表达式，⎧3-2 可控性问题基本概念考虑线性系统：3-3 可观测性的基本概念3-4 线性定常系统可控性判据考虑线性定常系统：例3-3 判断已知系统的可控性。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
作業 (20%)
正式考試 2 次 (各40%)
長庚大學電機系
State feedback and state estimation
Controller and observer design
Minimal realizations (option)
Measure of controllability (option)
長庚大學電機系
1-10
評 量 標 準
Theoretical analysis rather than trial and errors.
Theoretical analysis is important because
– physical system is usually too expensive or too dangerous to be experimented – thorough understanding of system behaviors
1-1
線 性 系 統 理 論 Linear System Theory
林心宇 長庚大學電機工程學系
2010秋
長庚大學電機系
1-2
教師資料
教師：林心宇
– – – – Office Room: 工學大樓六樓 Telephone: Ext. 3221 E-mail: shinylin@.tw Office Hour: 2:00 – 4:00 pm, Thursaourse
Broad applications cover many areas such as control systems, signal processing, communications, aeronautics, etc.
Availability of powerful toolbox MATLAB
長庚大學電機系
1-9
課 程 簡 介
Mathematical description of systems Review of Linear Algebra (when necessary)
State-space solutions and realization
Stability Controllability and observability
l unstretched l
1-8
l +s
m
x
m
s
x=0
equilibrium position mg – ks =0
in motion
– Observed from experiment: damping force ~ velocity – By Newton’s Law:
mg k (s x) x kx x mx x kx 0 mx
Interpretation
Analytic Solutions, Numerical Solutions, or Qualitative Analysis
Understanding Prediction system’s behavior)
Control (Change
長庚大學電機系
Spring/mass system:
長庚大學電機系
1-4
課程目標及背景需求
介紹如何以數學模式去分析線性系統，並 介紹穩定性、可控性、可觀測性、狀態迴 授及估測等重要觀念，以及如何設計控制 器、觀測器。 背景需求
– Linear Algebra – Elementary Differential Equation
長庚大學電機系
長庚大學電機系
1-6
Why Need Theoretical Background
To investigate more insight of system behavior
長庚大學電機系
1-7
Physical Model
Physical Laws
Mathematical Model
Solving
長庚大學電機系
1-3
教
• Textbook:
科
書
– C.-T. Chen, Linear System Theory and Design, 3rd Ed., Oxford University Press, 1999.
• Reference:
– T. Kailath, Linear Systems, Prentice-Hall, 1980.