第五节 传热过程的计算化工生产中广泛采用间壁换热方法进行热量的传递。
间壁换热过程由固体壁的导热和壁两侧流体的对流传热组合而成，导热和对流传热的规律前面已讨论过，本节在此基础上进一步讨论传热的计算问题。
化工原理中所涉及的传热过程计算主要有两类：一类是设计计算，即根据生产要求的热负荷，确定换热器的传热面积；另一类是校核计算，即计算给定换热器的传热量、流体的流量或温度等。
两者都是以换热器的热量衡算和传热速率方程为计算基础。
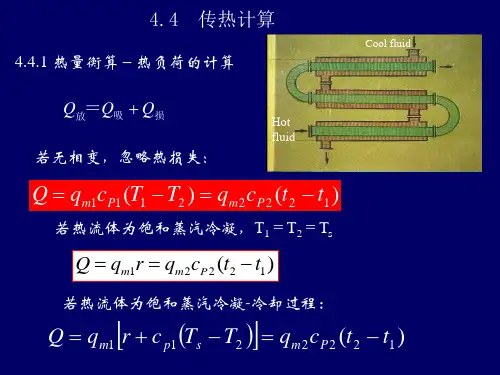
4-5-1 热量衡算流体在间壁两侧进行稳定传热时，在不考虑热损失的情况下，单位时间热流体放出的热量应等于冷流体吸收的热量，即：Q=Q c =Q h （4-59） 式中 Q ——换热器的热负荷，即单位时间热流体向冷流体传递的热量，W ； Q h ——单位时间热流体放出热量，W ； Q c ——单位时间冷流体吸收热量，W 。
若换热器间壁两侧流体无相变化，且流体的比热容不随温度而变或可取平均温度下的比热容时，式（4-59）可表示为()()1221t t c W T T c W Q pc c ph h -=-= （4-60） 式中 c p ——流体的平均比热容，kJ/（kg ·℃）； t ——冷流体的温度，℃； T ——热流体的温度，℃； W ——流体的质量流量，kg/h 。
若换热器中的热流体有相变化，例如饱和蒸气冷凝，则()12t t c W r W Q pc c h -== （4-61） 式中 W h ——饱和蒸气（即热流体）的冷凝速率，kg/h ； r ——饱和蒸气的冷凝潜热，kJ/kg 。
式（4-61）的应用条件是冷凝液在饱和温度下离开换热器。
若冷凝液的温度低于饱和温度时，则式（4-61）变为()[]()122t t c W T T c r W Q pc c s ph h -=-+= （4-62） 式中 c ph ——冷凝液的比热容，kJ/（kg ·℃）； T s ——冷凝液的饱和温度，℃。
