2018届高三数学一轮复习专项检测试题： 计数原理02含答案

内蒙古大学附中2018版《创新设》高考数学一轮复习单元能力提升训练：计数原理本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张.从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多1张.不同取法的种数为( )A ． 472B ． 252C ． 232D ． 484【答案】A2．现要从甲、乙、丙、丁、戊五人中选出三人担任班长、副班长、团支书三种不同的职务，且上届任职的甲、乙、丙都不再连任原职务．．．．．．．的方法种数为( ) A ．48 B ．30 C ．36 D ．32【答案】D3．现有男、女学生共7人，从男生中选1人，从女生中选2人分别参加数学、物理、化A ．男生4人，女生3人B ．男生3人，女生4人C ．男生2人，女生5人D ．男生5人，女生2人. 【答案】B4．512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2，则该展开式中常数项为( ) A ．-40 B ．-20 C ．20 D ．40【答案】D5．八个一样的小球按顺序排成一排，涂上红、白两种颜色，5个涂红色，三个涂白色，求恰好有个三个的连续的小球涂红色，则涂法共有( )A. 24种B. 30种C. 20种D. 36种【答案】A6．在8)1)(1(+-x x 的展开式中5x 的系数是( )A ．−14B ．14C ．−28D ．28【答案】B7．有不同的语文书9本,不同的数学书7本,不同的英语书5本,从中选出不属于同一的书2本,则不同的选法有( )种A ．21B ．315C ． 143D ．153【答案】C8．9名乒乓球运动员，男5名，女4名，现要从中选出2名男队员、2名女队员进行混合双打比赛，不同的配对方法共有( )A ．60种B ．84种C ．120种D ．240种【答案】C9．某种实验中，先后要实施个程序，其中程序A 只能出现在第一步或最后一步，程序B 和C 实施时必须相邻，请问实验顺序的编排方法共有( )A ．24种B ．48种C ．96种D ．144种【答案】C10．将字母a,a,b,b,c,c,排成三行两列，要求每行的字母互不相同，每列的字母也互不相同，则不同的排列方法共有( )A ．12种 B.18种 C.24种 D.36种【答案】A11．将9个相同的小球放入3个不同的盒子，要求每个盒子中至少有1个小球，且每个盒子中的小球个数都不同，则不同的放法共有( )A ．15种B ．18种C ．19种D ．21种【答案】B12．某单位拟安排6位员工在今年6月4日至6日(端午节假期)值班，每天安排2人，每人值班1天，若6位员工中的甲不值14日，乙不值16日，则不同的安排方法共有( )A ．30种B ．36种C ．42种D ．48种【答案】C第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．在5(23)x -的展开式中，各项系数的和为 ． [:数理化]【答案】1-14．设ABCDEF 为正六边形，一只青蛙开始在顶点A 处，它每次可随意地跳到相邻两顶点之一．若在5次之内跳到D 点，则停止跳动；若5次之内不能到达D 点，则跳完5次也停止跳动，那么这只青蛙从开始到停止，可能出现的不同跳法共 种．【答案】26[:15．在65)1()1(x x -+-的展开式中，含3x 的项的系数是【答案】-30[:16．用红、黄、蓝三种颜色之一去涂图中标号为9,,2,1 的9个小正方形（如右图），使得任意相邻（有公共边的）小正方形所涂颜色都不相同，且标号为“1、5、9”的小正方形涂相同的颜色，则符合条件的所有涂法共有 种．【答案】108 三、解答题 (本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．用0、1、2、3、4、5这六个数字，可以组成多少个分别符合下列条件的无重复数字的四位数： (1)奇数；(2)偶数；(3)大于3 125的数.【答案】 (1)先排个位，再排首位，共有A 13·A 14·A 24=144（个）.(2)以0结尾的四位偶数有A 35个，以2或4结尾的四位偶数有A 12·A 14·A 24个，则共有A 35+A 12·A 14·A 24=156（个）.(3)要比3 125大，4、5作千位时有2A 35个，3作千位，2、4、5作百位时有3A 24个，3作千位，1作百位时有2A 13个，所以共有2A 35+3A 24+2A 13=162（个）.18．有9名学生，其中2名会下象棋但不会下围棋，3名会下围棋但不会下象棋，4名既会下围棋又会下象棋；现在要从这9名学生中选出2名学生，一名参加象棋比赛，另一名参加围棋比赛，共有多少种不同的选派方法？【答案】设2名会下象棋但不会下围棋的同学组成集合A ，3名会下围棋但不会下象棋的同学组成集合B ，4名既会下围棋又会下象棋的同学组成集合C ，则选派2名参赛同学的方法可以分为以下4类：第一类：A 中选1人参加象棋比赛，B 中选1人参加围棋比赛，方法数为61312=⋅C C 种；第二类：C 中选1人参加象棋比赛，B 中选1人参加围棋比赛，方法数为121314=⋅C C 种；第三类：C 中选1人参加围棋比赛，A 中选1人参加象棋比赛，方法数为81214=⋅C C 种；第四类：C 中选2人分别参加两项比赛，方法数为1224=A 种；由分类加法计数原理，选派方法数共有：6+12+8+12=38种。

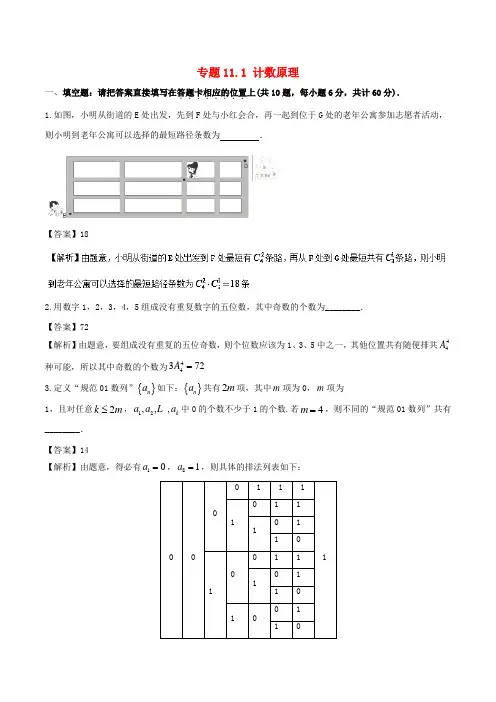
专题11.1 计数原理一、填空题：请把答案直接填写在答题卡相应的位置．．．．．．．．上(共10题，每小题6分，共计60分)． 1.如图，小明从街道的E 处出发，先到F 处与小红会合，再一起到位于G 处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为 ．【答案】182.用数字1，2，3，4，5组成没有重复数字的五位数，其中奇数的个数为________． 【答案】72【解析】由题意，要组成没有重复的五位奇数，则个位数应该为1、3、5中之一，其他位置共有随便排共44A 种可能，所以其中奇数的个数为44372A =3.定义“规范01数列”{}n a 如下：{}n a 共有2m 项，其中m 项为0，m 项为 1，且对任意2k m ≤，12,,,k a a a 中0的个数不少于1的个数.若4m =，则不同的“规范01数列”共有________． 【答案】14【解析】由题意，得必有10a =，81a =，则具体的排法列表如下：4.八个一样的小球按顺序排成一排，涂上红、白两种颜色，5个涂红色，三个涂白色，恰好有三个连续的小球涂红色，则涂法共有________． 【答案】 245. 将3张不同的奥运会门票分给10名同学中的3人，每人1张，则不同的分法种数有________． 【答案】720【解析】第1张有10种分法，第2张有9种分法，第3张有8种分法，∴一共有10×9×8＝720(种)． 6.六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有________种． 【答案】216【解析】最左端排甲，有5!120=种排法；最左端排乙，有44!96⨯=种排法，共有12096216+=种排法. 7. 2014年某通讯公司推出一组手机卡号码，卡号的前七位数字固定，后四位数从“0000”到“9999”共10000个号码.公司规定：凡卡号的后四位带数字“5”或“8”的一律作为“金马卡”，享受一定优惠政策，则这组号码中“金马卡”的个数为________． 【答案】5904【解析】先考虑卡号的后四位不带数字“5”与“8”的号码共有4864644096=⨯=个，所以卡号前七位数字固定，后四位带数字“中5”或“8”的卡号共有1000040965904-=个.8.某班2名同学准备报名参加浙江大学、复旦大学和上海交大的自主招生考试，要求每人最多选报两所学校，则不同的报名结果有________种． 【答案】3639. 如图所示的五个区域中，中心区域是一幅图画，现有要求在其余四个区域中涂色，现有四种颜色可供选择．要求每一个区域只涂一种颜色，相邻区域所涂颜色不同，则不同的涂色方法种数为________．【答案】84【解析】分成两类：A 和C 同色时有4×3×3＝36(种)；A 和C 不同色时4×3×2×2＝48(种)，∴一共有36＋48＝84(种)．10.将一个四棱锥的每个顶点染上一种颜色，并使同一条棱上的两个端点异色，若只有5种颜色可供使用,则不同的染色方法总数有________种． 【答案】420【解析】设四棱锥为P ABCD -，下面分：①C 与B 同色；②C 与B 不同色两种情况讨论．①C 与B 同色：111543:,:,:,P C A C B C C 与B 同色：1，13:D C ，共有11115433C C C C 种；②C 与B 不同色：111543:,:,:,P C A C B C C 与B 不同色：1122,:CD C ，共有1111154322C C C C C 种．由分步计数原理得总共有111111111543354322420C C C C C C C C C +=种不同的染色方法．二、解答题：解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内．．．．．。

成都理工大学附中2018高三数学一轮高考单元辅导与训练单元检测：计数原理 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷 (选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．若变量,a b 满足约束条件6321a b a b a +≤⎧⎪-≤-⎨⎪≥⎩，23n a b =+，则n 取最小值时，21n x ⎛⎫ ⎪⎝⎭二项展开式中的常数项为( ) A ． -80 B ．80C ．40D ．-20【答案】A2．25人排成5×5方阵，从中选出3人，要求其中任意2人既不同行也不同列，则不同的选法为( )A ．60种B ．100种C ．300种D ．600种【答案】D 3．在()()x x --216的展开式中，3x 的系数是( )A ．－55B ．45C ． －25D ．25【答案】A4．若(1＋2x)5＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4＋a 5x 5，则a 0＋a 1＋a 3＋a 5＝( )A ． 122B ． 123C ． 243D ． 244【答案】B5．由1，2，3，4组成没有重复数字的三位数的个数为( )A ． 36B ． 24C ． 12D ．6【答案】B6．自然数1，2，3，…，n 按照一定的顺序排成一个数列：12 n a a a ⋯，，，.若满足12a a -1+-24n a n -≤++，则称数列12 n a a a ⋯，，，为一个“优数列”.当6n =时，这样的“优数列”共有( )A ．24个B ．23个C ．18个D ．16个 【答案】A7．有6个座位连成一排，现有3人就坐，则恰有两个空座位相邻的不同坐法有( )A ．36种B ．48种C ．72种D ．96种 【答案】C8．将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有( ) 种 A ．12 B ．10C ．9D ．8【答案】A9．庆“元旦”的文艺晚会由6个节目组成，演出顺序有如下要求：节目甲必须安排往前两位，节目乙不能安排在第一位，节目丙必须安排在最后一位，则该晚会节目演出顺序的编排方案共有( ) A ．36种； B ．42种；C ．48种；D ．54种【答案】B10．已知两个实数集合A={a 1, a 2, … , a 100}与B={b 1, b 2, … , b 50}，若从A 到B 的映射f 使得B 中的每一个元素都有原象，且f(a 1)≤f(a 2)≤…≤f(a 100)，则这样的映射共有( )A ． 50100C B ． 5090CC ． 49100CD ． 4999C【答案】D11．若n1)x的展开式中各项系数之和为125,则展开式中的常数项为( ) A ．-27 B ．-48C ．27D ．48【答案】D12．从6名学生中，选出4人分别从事A 、B 、C 、D 四项不同的工作，若其中，甲、乙两人不能从事工作A ，则不同的选派方案共有( ) A ．96种 B ．180种 C ．240种D ．280种【答案】C第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．今有2个红球、4个黄球，同色球不加以区分，将这6个球排成一列有____种不同的方法（用数字作答）． 【答案】1514．62)21(x x -展开式中6x 的系数是 。

计数原理01一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．设m∈N*，且m＜25，则(25－m)(26－m)…(30－m)等于( )A．625mA-B．2530mmA--C．630mA-D．530mA-【答案】C2．把10)x-把二项式定理展开，展开式的第8项的系数是( )A．135B．135-C．-D．【答案】D3．球面上有七个点，其中四个点在同一个大圆上，其余无三点共一个大圆，也无两点与球心共线，那么经过球心与球面上的任意两点可作球的大圆有( )A．15个B．16个C．31个D．32个【答案】B4．西大附中数学组有实习老师共5名，现将他们分配到高二年级的1、2、3三个班实习，每班至少1名，最多2名，则不同的分配方案有( )A．30种B．90种C．180种D．270种【答案】B5．6位好朋友在一次元旦聚会中进行礼品交换，任意两位朋友之间最多交换一次，进行交换的两位朋友互赠一份礼品，已知这6位好朋友之间共进行了13次互换，则收到4份礼品的同学人数为( )A ．1或4B ．2或4C ．2或3D ．1或3【答案】B6．从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a ，b 组成复数a ＋bi ，其中虚数有( )A ．30个B ．42个C ．36个D ．35个【答案】C7．编号为1、2、3、4、5、6、7的七盏路灯，晚上用时只亮三盏灯，且任意两盏亮灯不相邻，则不同的开灯方案有( )A ．60B ．20种C ．10种D ．8种【答案】C8．设数列{}n a 的前n 项和为n S ，令n S S S T n n +⋯++=21，称n T 为数列1a ，2a ，……，n a 的“理想数”，已知数列1a ，2a ，……，500a 的“理想数”为2004，那么数列8，1a ，2a ，……，500a 的“理想数”为( )A ．2008B ．2009C ．2010D ．2011【答案】A9．现有男、女学生共7人，从男生中选1人，从女生中选2人分别参加数学、物理、化学三科竞赛，共有108种不同方案，那么男、女生人数分别是( )A ．男生4人，女生3人B ．男生3人，女生4人C ．男生2人，女生5人D ．男生5人，女生2人.【答案】B10．某班由24名女生和36名男生组成，现要组织20名学生外参观，若这20名学生按性别分层抽样产生，则参观团的组成法共有( )A ．824C 1236C 种B ．81224.36AC 种 C ．10102436C C 种D ．2060C 种【答案】A11．3张不同的电影票全部分给10个人,每人至多一张,则有不同分法的种数是( )A ．1260B ．120C ．240D ．720【答案】D12．计划在4个体育馆举办排球、篮球、足球3个项目的比赛，每个项目的比赛只能安排在一个体育馆进行，则在同一个体育馆比赛的项目不超过2项的安排方案共有( )A ．24种B ．36种C ．42种D ．60种 【答案】D二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．n x)1( 的展开式中，某一项的系数为7，则展开式中第三项的系数是________．【答案】2114．某同学有同样的画册2本，同样的集邮册3本，赠送给5位朋友，每位朋友1本，则不同的赠送方法共有种.【答案】1015．7名志愿者中安排6人在周六、周日两天参加社区公益活动．若每天安排3人，则不同的安排方案共有种(用数字作答)。

2018高考数学一轮复习计数原理专题检测试题及答案一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．用数字1，2，3，4，5可以组成没有重复数字，并且比20000大的五位偶数共有( ) A．48个B．36个C．24个D．18个【答案】B2．六名学生从左至右站成一排照相留念，其中学生甲和学生乙必须相邻．在此前提下，学生甲站在最左侧且学生丙站在最右侧的概率是( )A．1301B．10C．140D．120【答案】C3．已知复数a bi，其中a,b为0，1，2，…，9这10个数字中的两个不同的数，则不同的虚数的个数为( )A．36 B．72 C．81 D．90【答案】C4．由1,2,3,4,5,6组成无重复数字且1,3都不与5相邻的六位偶数的个数是( ) A．72 B．96 C．108 D．144【答案】C5．将标号为1、2、3、4、5、6的6张卡片放入3个不同的信封中，若每个信封放2张，其中标号为3，6的卡片放入同一信封，则不同的方法共有( )种A．54 B．18 C．12 D．36【答案】A6．把语文、数学、英语、物理、化学这五门课程安排在一天的五节课里，如果数学必须比化学先上，则不同的排法有( )A．48 B．24 C．60 D．120【答案】C7．(1i)10 (i为虚数单位) 的二项展开式中第七项为( )A．120 i B．210 C．210 D．120 i【答案】C8．从5位男实习教师和4位女实习教师中选出3位教师派到3个班实习班主任工作，每班派一名，要求这3位实习教师中男女都要有，则不同的选派方案共有( )A．210 B．420 C．630 D．840【答案】B9．庆“元旦”的文艺晚会由6个节目组成，演出顺序有如下要求：节目甲必须安排往前两位，节目乙不能安排在第一位，节目丙必须安排在最后一位，则该晚会节目演出顺序的编排方案共有( )A．36种；B．42种；C．48种；D．54种【答案】B- 1 -a10．()5（x R）展开式中x3的系数为10，则实数a等于( ) xxA．-1 B．12C． 1 D．2【答案】D81x11．在的展开式中的常数项是( )32xA．7B．7C．28D．28【答案】A312．若(x)n展开式中存在常数项，则n的最小值为( )3xA．５B．６C．７D．８【答案】A二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．某地教育部门欲派5名工作人员到3所学校进行地震安全教育，每所学校至少1人，至多派2人，则不同的安排方案共有种。

第十二章 计数原理第一节 两个基本计数原理题型135 分类加法计数原理与分步乘法计数原理1.（2107浙江16）从6男2女共8名学生中选出队长1人，副队长1人，普通队员2人组成4人服务队，要求服务队中至少有1名女生，共有 种不同的选法.（用数字作答）1.解析 解法一（间接法）：分2步完成：第一步，8名学生中选4人（至少有1名女生），即8名学生中任选4人去掉全是男生的情况有4486C C -种选法；第二步，分配职务，4人里选2人担任队长和副队长有24A 种选法．所以共有()()442864C C A 701512660-⋅=-⨯=种选法．解法二（直接法）：分2步完成：第一步，8名学生中选4人（至少有1名女生），其中1女3男有1326C C 种选法，2女2男有2226C C 种选法；第二步，分配职务，4人里选2人担任队长和副队长有24A 种选法．所以共有 ()()1322226264C C C C A 22011512660+⋅=⨯+⨯⨯=种选法．第二节 排列与组合题型136 与排列相关的常见问题 题型137 与组合相关的常见问题题型138 排列与与组合综合的常见问题——暂无2.（2017天津理14）用数字1，2，3，4，5，6，7，8，9组成没有重复数字，且至多有一个数字是偶数的四位数，这样的四位数一共有___________个（用数字作答）.2.解析 依题意按分类计数原理操作：(1)当没有一个数字是偶数时，从1，3，5，7，9这五个数字中任取四个数，再进行全排列得无重复数字的四位数有45A 120=个(或4454C A 120=个)；(2)当仅有一个数字是偶数时，先从2，4，6，8中任取一个数，再从1，3，5，7，9中任取三个数，然后再进行全排列得到无重复数字的四位数有134454C C A 960=.故由分类计数原理得这样的四位数共有1209601080N =+=个.3.（2017全国2卷理科6）安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有（ ）.A ．12种B ．18种C ．24种D ．36种3．解析 只能是一个人完成2项工作，剩下的2人各完成一项工作．由此把4项工作分成3份再全排得2343C A 36⋅=.故选D.第三节 二项式定理题型139 二项式定理展开式的通项及系数4．（2017浙江13）已知多项式()()32543211234512x x x a x a x a x a x a +++++++=，则4a =___________，5a =________.4.解析 32322(1)(2)(331)(44)x x x x x x x ++=+++++，所以412416a =+=，54a =．5.（2107山东理11）已知()13nx +的展开式中含有2x 项的系数是54，则n = .5. 解析 ()1C 3C 3rr r r r r n n T x x +==⋅⋅，令2r =，得22C 354n ⋅=，解得4n =．6.（2017全国3卷理科4）()()52x y x y +-的展开式中33x y 的系数为（ ）.A ．80-B ．40-C ．40D ．806．解析 由二项式定理可得，原式展开中含33x y 的项为()()()()23322355C 2C 2x x y y x y ⋅-+⋅-=3340x y ，则33x y 的系数为40，故选C. 7.（2017全国1卷理科6）()62111x x ⎛⎫++ ⎪⎝⎭展开式中2x 的系数为（ ）. A.15 B.20 C.30 D.357. 解析 ()()()66622111+1111x x x x x ⎛⎫+=⋅++⋅+ ⎪⎝⎭，对()61x +二项式展开中2x 项的系数为2665C 152⨯==，对()6211x x ⋅+二项式展开中2x 项的系数为46C =15，所以2x 的系数为151530+=.故选C.。

2018高考文科数计数原理专项100题（WORD版含答案）一、选择题（本题共31道小题）1.21个人按照以下规则表演节目：他们围坐一圈，按顺序从1到3循环报数，报数字“3”的人出来表演节目，并且表演过的人不再参加报数，那么在仅剩两个人没有表演过节目的时候，共报数的次数为（）A．19 B．38 C．51 D．572.甲、乙、丙三人站到共有7级的台阶上，若每级台阶最多站2人，同一级台阶上的人不区分站的位置，则不同的站法种数是（）A．258 B．306 C．336 D．2963.若（3x﹣）n展开式中各项系数之和为32，则该展开式中含x3的项的系数为（）A．﹣5 B．5 C．﹣405 D．4054.现有2门不同的考试要安排在5天之内进行，每天最多进行一门考试，且不能连续两天有考试，那么不同的考试安排方案种数有（）A．6 B．8 C．12 D．165.为便民惠民，某通信运营商推出“优惠卡活动”．其内容如下：卡号的前7位是固定的，后四位从“0000”到“9999”共10000个号码参与该活动，凡卡号后四位带有“6”或“8”的一律作为优惠卡，则“优惠卡”的个数是（）A．1980 B．4096 C．5904 D．80206.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”．该表由若干行数字组成，从第二行起，每一行中的数字均等于其“肩上”的两数之和，表中最后一行仅是一个数，则这个数为（）A．2018×22016B．2018×22015C．2017×22016D．2017×220157.二项式（2x 2﹣）5的展开式中第四项的系数为（ ） A ．﹣40 B ．10 C ．40 D ．﹣208.某小组有男生8人，女生3人，从中随机抽取男生1人，女生2人，则男生甲和女生乙都被抽到的概率为（ ） A ． 61 B ．81C ． 121D ． 2419.3名医生和6名护士被分配到3所学校为学生体检，每校分配1名医生和2名护士．不同的分配方法共有（ ） A ．90种 B ．180种C ．270种D ．540种10.4(1)x 的展开式中2x 的系数为 ( )A. 1B.4C.6D.12 11.某生产基地有五台机器，现有五项工作待完成，每台机器完成每项工作后获得的效益值 如表所示．若每台机器只完成一项工作，且完成五项工作后获得的效益值总和最大，则 下列叙述正确的是A ．甲只能承担第四项工作B ．乙不能承担第二项工作C ．丙可以不承担第三项工作D ．获得的效益值总和为78 12.用数字0，1，2，3，4，5组成没有重复数字的五位数，其中比40000大的偶数共有（ ） A ．144个 B ．120个C ．96个D ．72个13.若（x6）n的展开式中含有常数项，则n 的最小值等于( )A ．3B ．4C ．5D ．614.某班班会准备从甲、乙等7名学生中选派4名学生发言，要求甲、乙两人至少有一人参加，当甲乙同时参加时，他们两人的发言不能相邻，那么不同的发言顺序的种数为（ ） A ．360 B ．520 C ．600 D ．72015.设二项式1)n x的展开式的各项系数和为p ，所有二项式系数的和是s ，若272p s +=，则n =A.6B.5C.4D.8 16.51()(21)ax x x+-的展开式中各项系数的和为2，则该展开式中常数项为(▲)A ．－20B ．－10C ．10D ．2017.有6名男医生、5名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有( )A. 60种B. 70种C. 75种D. 150种18.某班级要从4名男生、2名女生中选派4人参加某次社会活动，如果要求至少有1名女生．那么不同的选派方法共有（ ）A ．14种B ．28种C ．32种D ．48种 19.将2名教师6名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和3名学生组成，不同的安排方案共有 (A)240种 (B)120种 (C)40种 (D)20种20.将2名男生,4名女生分成两个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名男生和2名女生组成,不同的安排方案共有( ))(A 12种)(B 10种 )(C 9种 )(D 8种21.7(1)x +的展开式中2x 的系数是( ))(A 42 )(B 35 )(C 28 )(D 2122.一支人数是5的倍数且不少于1000人的游行队伍，若按每横排4人编队，最后差3人；若按每横排3人编队，最后差2人；若按每横排2人编队，最后差1人．则这只游行队伍的最少人数是( ) A ．1025B ．1035C ．1045D ．105523.将2n 个正整数1、2、3、…、2n （2n ≥）任意排成n 行n 列的数表.对于某一个数表,计算各行和各列中的任意两个数a 、b （a b >）的比值ab,称这些比值中的最小值为这个数表的“特征值”.当2n =时,数表的所有可能的“特征值”最大值为 A ．32 B ．43C ． 2D ． 324.61)x的展开式中常数项等于 A ．1 5B ．一l 5C ．20D ．一2025.二项式102x ⎛⎝的展开式中的常数项是A.第10项B.第9项C.第8项D.第7项 26.6(42)xx -+的展开式的常数项是（ ）（A ）1 （B ）6 （C ）15 （D ）2027.一支人数是5的倍数且不少于1000人的游行队伍，若按每横排4人编队，最后差3人；若按每横排3人编队，最后差2人；若按每横排2人编队，最后差1人．则这只游行队伍的最少人数是 A ．1025B ．1035C ．1045D ．105528.从8名网络歌手中选派4名同时去4个地区演出（每地1人），其中甲和乙只能同去或同不去，甲和丙不同去，则不同的选派方案共有多少种（ ）A ．240B ．360C ．480D ．60029.在7)1(ax +的展开式中，含x 5与x 4项的系数相等，则a 的值是 （ ）30.从9名学生中选出4人参加辨论比赛，其中甲、乙、丙三人至少有两人入选的不同选法的种数为 (A) 36.(B) 96.(C) 63. (D) 51.31.下列等式不成立的是（n ＞m≥1，m ，n ∈Z ）（ ） A ．= B ． +=C ．是奇数D ．=53-35-5335二、填空题（本题共67道小题）32.6个人站成一排，若甲、乙两人之间恰有2人，则不同的站法种数为 ． 33.如果一条直线与一个平面平行，那么称此直线与平面构成一个“平面线面组”．在一个长方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“平行线面组”的个数是 ． 34.现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张．从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多1张．不同取法的种数为 ．（用数字作答） 35.{a n }是无穷数列，若{a n }是二项式（1+2x ）n （n ∈N +）展开式各项系数和，则（++…+）= ．36.在（3﹣x ）7的展开式中，x 5的系数是 （用数字作答）． 37.已知2个小孩和3个大人排队，其中2个小孩不能相邻，则不同的排法种数有 种． 38.若（﹣）a的展开式中只有第5项的二项式系数最大，则展开式中常数项是 ．39.表示一个两位数，记f （n ）=a+b+a ×b ，如f （12）=1+2+1×2=5，则满足f（n ）=n 的两位数共有 个． 40.在（1﹣x ）11的展开式中系数最大的是第 项． 41.如果3nx ⎛⎫ ⎝的展开式中各项系数之和为128，则含31x 项的系数等于 ．（用数字作答） 42.在831⎪⎭⎫ ⎝⎛-x x 的展开式中，其常数项的值为 .43.设关于x 的实系数不等式2(3)()0ax x b +-…对任意[0,)x ∈+∞恒成立，则2a b = . 44.在代数式5221(425)1x x x ⎛⎫--+ ⎪⎝⎭的展开式中，常数等于 .45.已知在62⎪⎭⎫ ⎝⎛+x k x （k 为常数）的展开式中，3x 项的系数等于160，则=k _____________．46.在（a+b ）n的二项展开式中，若二项式系数的和为256，则二项式系数的最大值为 （结果用数字作答）． 47.若二项式展开式中含x 2项的系数为，则= ．48.在上海高考改革方案中，要求每位高中生必须在物理、化学、生物、政治、历史、地理6门学科（3门理科学科，3门文科学科）中选择3门学科参加等级考试，小丁同学理科成绩较好，决定至少选择两门理科学科，那么小丁同学的选科方案有 种． 49.若的二项展开式中各项的二项式系数的和是64，则n= ，展开式中的常数项为 ．（用数字作答） 50.在（1+x+）10的展开式中，x 2项的系数为 （结果用数值表示）．51.已知10()(21)f x x =-1098109810a x a x a x a x a =+++⋅⋅⋅++，则222223344C a C a C a +++21010C a ⋅⋅⋅+=52.在（1+x ）5﹣（1+x ）6的展开式中，含x 3的项的系数是 ．53. 已知展开式中二项式系数之和为1024，则含x 2项的系数为 ．54.（5分）（2015•钦州模拟）已知的展开式中，常数项为14，则a=（用数字填写答案）． 55.用数字“1，2”组成一个四位数，则数字“1，2”都出现的四位数有 个． 56.（4分）四面体的顶点和各棱中点共有10个点，取其中不共面的4点，不同的取法共有 种． 57.在二项式（x ﹣）5的展开式中，含x 5项的系数为 ．（结果用数值表示）58.设8780178(1)x a a x a x a x -=++++ ，则0178||||||||a a a a ++++= . 59.一个不透明袋中有10个不同颜色的同样大小的球，从中任意摸出2个，共有 种不同结果（用数值作答）.60.甲、乙两名同学各自等可能地从数学、物理、化学、生物四个兴趣小组中选择一个小组参加活动，则他们选择相同小组的概率为 。

高考数学一轮复习分类加法计数原理专题检测（带答案）完成一件事，有n类方法，在第1类方法中有m1种不同的方法，在第2类方法中有m2种不同的方法‥‥‥，在第n类方法中有mn种不同的方法，以下是分类加法计数原理专题检测，请考生及时练习。

一、选择题1.如图，用4种不同的颜色涂入图中的矩形A，B，C，D中，要求相邻的矩形涂色不同，那么不同的涂法有()A.72种B.48种C.24种D.12种解析先分两类：一是四种颜色都用，这时A有4种涂法，B 有3种涂法，C有2种涂法，D有1种涂法，共有4321=24种涂法;二是用三种颜色，这时A，B，C的涂法有432=24种，D只需不与C同色即可，故D 有2种涂法.故不同的涂法共有24+242=72种.答案 A2.如图，用6种不同的颜色把图中A、B、C、D四块区域分开，假定相邻区域不能涂同一种颜色，那么不同的涂法共有().A.400种B.460种C.480种D.496种解析从A末尾，有6种方法，B有5种，C有4种，D、A同色1种，D、A不同色3种，不同涂法有654(1+3)=480(种)，应选C.答案 C3.某省高中学校自实施素质教育以来，先生社团失掉迅猛开展，某校高一重生中的五名同窗计划参与春晖文学社、舞者轮滑俱乐部、篮球之家、围棋苑四个社团.假定每个社团至少有一名同窗参与，每名同窗至少参与一个社团且只能参与一个社团.且同窗甲不参与围棋苑，那么不同的参与方法的种数为().A.72B.108C.180D.216解析设五名同窗区分为甲、乙、丙、丁、戊，由题意，假设甲不参与围棋苑，有以下两种状况：(1)从乙、丙、丁、戊中选一人(如乙)参与围棋苑，有C种方法，然后从甲与丙、丁、戊共4人中选2人(如丙、丁)并成一组与甲、戊分配到其他三个社团中，有CA种方法，故共有CCA种参与方法;(2)从乙、丙、丁、戊中选2人(如乙、丙)参与围棋苑，有C 种方法，甲与丁、戊分配到其他三个社团中有A种方法，这时共有CA种参与方法;综合(1)(2)，共有CCA+CA=180种参与方法.答案 C.有4位教员在同一年级的4个班中各教一个班的数学，在数学检测时要求每位教员不能在本班监考，那么监考的方法有()A.8种B.9种C.10种D.11种解析分四步完成，共有3311=9种.答案 B.从6人中选4人区分到巴黎、伦敦、悉尼、莫斯科四个城市旅游，要求每个城市有一人旅游，每人只旅游一个城市，且这6人中甲、乙两人不去巴黎旅游，那么不同的选择方案共有().A.300种B.240种C.144种D.96种解析甲、乙两人不去巴黎旅游状况较多，采用扫除法，契合条件的选择方案有CA-CA=240.答案 B.4位同窗从甲、乙、丙3门课程中选修1门，那么恰有2人选修课程甲的不同选法有().A.12种B.24种C.30种D.36种解析分三步，第一步先从4位同窗中选2人选修课程甲.共有C种不同选法，第二步给第3位同窗选课程，有2种选法.第三步给第4位同窗选课程，也有2种不同选法.故共有C22=24(种).答案 B二、填空题.将数字1,2,3,4,5,6按第一行1个数，第二行2个数，第三行3个数的方式随机陈列，设Ni(i=1,2,3)表示第i行中最大的数，那么满足N1解析由数字6一定在第三行，第三行的排法种数为AA=60;剩余的三个数字中最大的一定排在第二行，第二行的排法种数为AA=4，由分步计数原理满足条件的陈列个数是240.答案 240.数字1,2,3，，9这九个数字填写在如图的9个空格中，要求每一行从左到右依次增大，每列从上到下也依次增大，当数字4固定在中心位置时，那么一切填写空格的方法共有________种.解析必有1、4、9在主对角线上，2、3只要两种不同的填法，关于它们的每一种填法，5只要两种填法.关于5的每一种填法，6、7、8只要3种不同的填法，由分步计数原理知共有223=12种填法.答案 12.假设把个位数是1，且恰有3个数字相反的四位数叫做好数，那么在由1,2,3,4四个数字组成的有反双数字的四位数中，好数共有________个.解析当相反的数字不是1时，有C个;当相反的数字是1时，共有CC个，由分类加法计数原理得共有好数C+CC=12个. 答案 12给n个自上而下相连的正方形着黑色或白色.当n4时，在一切不同的着色方案中，黑色正方形互不相邻的着色方案如以下图所示：由此推断，当n=6时，黑色正方形互不相邻的着色方案共有__________种，至少有两个黑色正方形相邻的着色方案共有________种.(结果用数值表示)三、解答题.如下图三组平行线区分有m、n、k条，在此图形中(1)共有多少个三角形?(2)共有多少个平行四边形?解 (1)每个三角形与从三组平行线中各取一条的取法是逐一对应的，由分步计数原理知共可构成mnk个三角形. (2)每个平行四边形与从两组平行线中各取两条的取法是逐一对应的，由分类和分步计数原理知共可构成CC+CC+CC个平行四边形..设集合M={-3，-2，-1,0,1,2}，P(a，b)是坐标平面上的点，a，bM.(1)P可以表示多少个平面上的不同的点?(2)P可以表示多少个第二象限内的点?(3)P可以表示多少个不在直线y=x上的点?解 (1)分两步，第一步确定横坐标有6种，第二步确定纵坐标有6种，经检验36个点均不相反，由分步乘法计数原理得N=66=36(个).(2)分两步，第一步确定横坐标有3种，第二步确定纵坐标有2种，依据分步乘法计数原理得N=32=6个.(3)分两步，第一步确定横坐标有6种，第二步确定纵坐标有5种，依据分步乘法计数原理得N=65=30个..现布置一份5天的任务值班表，每天有一团体值班，共有5团体，每团体都可以值多天班或不值班，但相邻两天不准由同一团体值班，问此值班表共有多少种不同的排法?可将星期一、二、三、四、五分给5团体，相邻的数字不分给同一团体.星期一：可分给5人中的任何一人，有5种分法;星期二：可分给剩余4人中的任何一人，有4种分法;星期三：可分给除去分到星期二的剩余4人中的任何一人，有4种分法;同理星期四和星期五都有4种不同的分法，由分步计数原理共有54444=1 280种不同的排法..集合A={a1，a2，a3，a4}，B={0,1,2,3}，f是从A到B的映射.(1)假定B中每一元素都有原象，这样不同的f有多少个?(2)假定B中的元素0必无原象，这样的f有多少个?(3)假定f满足f(a1)+f(a2)+f(a3)+f(a4)=4，这样的f又有多少个?(1)显然对应是逐一对应的，即为a1找象有4种方法，a2找象有3种方法，a3找象有2种方法，a4找象有1种方法，所以不同的f共有4321=24(个).(2)0必无原象，1,2,3有无原象不限，所以为A中每一元素找象时都有3种方法.所以不同的f共有34=81(个). (3)分为如下四类：第一类，A中每一元素都与1对应，有1种方法;第二类，A中有两个元素对应1，一个元素对应2，另一个元素与0对应，有CC=12种方法;第三类，A中有两个元素对应2，另两个元素对应0，有CC=6种方法;第四类，A中有一个元素对应1，一个元素对应3，另两个元素与0对应，有CC=12种方法.所以不同的f共有1+12+6+12=31(个).分类加法计数原理专题检测及答案的全部内容就是这些，查字典数学网预祝广阔考生可以考上理想的大学。

核心考点解读——计数原理个不同的步骤，在第一个步骤中有两个计数原理的区别在于完成事情的方法是可以完成事情的所有，还是完成事情的：二项展开式的通项，即1．（2017高考新课标I ，理6）621(1)(1)x x++展开式中2x 的系数为 A ．15B ．20C ．30D ．352．（2017高考新课标II ，理6）安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有 A ．12种B ．18种C ．24种D ．36种3．（2017高考新课标III ，理4）错误！未找到引用源。

的展开式中错误！未找到引用源。

的系数为 A ．错误！未找到引用源。

B ．错误！未找到引用源。

C ．40D ．804.(2016高考新课标I ，理14) 5(2x 的展开式中，x 3的系数是 .（用数字填写答案）5.(2016高考新课标II ，理5)如图，小明从街道的E 处出发，先到F 处与小红会合，再一起到位于G 处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为A ．24B ．18C ．12D ．96.(2016高考新课标III ，理12)定义“规范01数列”{a n }如下：{a n }共有2m 项，其中m 项为0，m 项为1，且对任意2k m ≤，12,,,k a a a 中0的个数不少于1的个数.若m =4，则不同的“规范01数列”共有A ．18个B ．16个C ．14个D ．12个7．(2015高考新课标I ，理10)25()x x y ++的展开式中，52x y 的系数为 A.10 B.20C.30D.608. (2015高考新课标II ，理15)4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32，则a =__________．1．已知的展开式中常数项为，则的值为A.B.C.D.2．党的十九大报告指出，建设教育强国是中华民族伟大复兴的基础工程，必须把教育事业放在优先位置，深化教育资源的均衡发展.现有4名男生和2名女生主动申请毕业后到两所偏远山区小学任教.将这6名毕业生全部进行安排，每所学校至少安排2名毕业生，则每所学校男女毕业生至少安排一名的概率为 A. 错误！未找到引用源。

计数原理
一、选择题(本大题共个小题，每小题分，共分，在每小题给出的四个选项中，只有一项是符合题目要求的)
．设∈*，且＜，则(－)(－)…(－)等于( )
．．．．
【答案】
．把把二项式定理展开，展开式的第项的系数是( ) ．．．．
【答案】
．球面上有七个点，其中四个点在同一个大圆上，其余无三点共一个大圆，也无两点与球心共线，那么经过球心与球面上的任意两点可作球的大圆有( )
．个．个．个．个
【答案】
．西大附中数学组有实习老师共名，现将他们分配到高二年级的、、三个班实习，每班至少名，最多名，则不同的分配方案有( )
．种．种．种．种
【答案】
．位好朋友在一次元旦聚会中进行礼品交换，任意两位朋友之间最多
交换一次，进行交换的两位朋友互赠一份礼品，已知这位好朋友之间共进行了次互换，则收到份礼品的同学人数为( )
．或．或．或．或
【答案】
．从集合{}中任取两个互不相等的数，组成复数＋，其中虚数有( ) ．个．个．个．个
【答案】
．编号为、、、、、、的七盏路灯，晚上用时只亮三盏灯，且任意两盏亮灯不相邻，则不同的开灯方案有( )
．．种．种．种
【答案】
．设数列的前项和为，令，称为数列，，……，的“理想数”，已知数列，，……，的“理想数”为，那么数列，，，……，
的“理想数”为( )
．．．．
【答案】。

“计数原理”双基过关检测一、选择题1．(2017·滨州模拟)甲、乙两人从4门课程中选修2门，则甲、乙所选课程中恰有1门相同的选法有( )A．6种B．12种C．24种D．30种解析：选C 分步完成：第一步，甲、乙选同一门课程有4种方法；第二步，甲从剩余的3门课程选一门有3种方法；第三步，乙从剩余的2门中选出一门课程有2种方法；∴甲、乙恰有1门相同课程的选法有4×3×2＝24(种)．2.现有4种不同颜色要对如图所示的四个部分进行着色，要求有公共边界的两块不能用同一种颜色，则不同的着色方法共有( )A．24种B．30种C．36种D．48种解析：选D 按A→B→C→D顺序分四步涂色，共有4×3×2×2＝48(种)．3．(2017·云南师大附中适应性考试)在(a＋x)7展开式中x4的系数为280，则实数a 的值为( )A．1 B．±1C．2 D．±2解析：选C 由题知，C47a3＝280，得a＝2，故选C.4．(2016·佛山二模)教学大楼共有五层，每层均有两个楼梯，由一层到五层的走法有( )A．10种B．25种C．52种D．24种解析：选D 每相邻的两层之间各有2种走法，共分4步．由分步乘法计数原理，共有24种不同的走法．5．张、王两家夫妇各带一个小孩一起到动物园游玩，购票后排队依次入园．为安全起见，首尾一定要排两位爸爸，另外，两个小孩一定要排在一起，则这六人入园顺序的排法种数为( )A．12 B．24C．36 D．48解析：选B 将两位爸爸排在两端，有2种排法；将两个小孩视作一人与两位妈妈任意排在中间的三个位置上，有2A 33种排法，故总的排法有2×2×A 33＝24(种)．6．某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人)，其中甲和乙不同去，甲和丙只能同去或同不去，则不同的选派方案种数是( )A ．150B ．300C ．600D ．900解析：选C 若甲去，则乙不去，丙去，再从剩余的5名教师中选2名，有C 25×A 44＝240种方法；若甲不去，则丙不去，乙可去可不去，从6名教师中选4名，共有C 46×A 44＝360种方法．因此共有600种不同的选派方案．7．(2017·成都一中模拟)设(x 2＋1)(2x ＋1)9＝a 0＋a 1(x ＋2)＋a 2(x ＋2)2＋…＋a 11(x ＋2)11，则a 0＋a 1＋a 2＋…＋a 11的值为( )A ．－2B ．－1C ．1D ．2解析：选A 令等式中x ＝－1，可得a 0＋a 1＋a 2＋…＋a 11＝(1＋1)(－1)9＝－2，故选A.8．从1,3,5,7,9这五个数中，每次取出两个不同的数分别记为a ，b ，共可得到lg a －lg b 的不同值的个数是( )A ．9B ．10C ．18D ．20解析：选C lg a －lg b ＝lg ab，从1,3,5,7,9中任取两个数分别记为a ，b ，共有A 25＝20种结果，其中lg 13＝lg 39，lg 31＝lg 93，故共可得到不同值的个数为20－2＝18.故选C.二、填空题9.⎝ ⎛⎭⎪⎫2x －1x 5的二项展开式中x 项的系数为________．解析：⎝ ⎛⎭⎪⎫2x －1x 5的展开式的通项是T r ＋1＝C r 5·(2x )5－r ·⎝ ⎛⎭⎪⎫－1x r ＝C r 5·(－1)r ·25－r ·x5－2r.令5－2r ＝1得r ＝2.因此⎝ ⎛⎭⎪⎫2x －1x 5的展开式中x 项的系数是C 25·(－1)2·25－2＝80.答案：8010．(2016·石家庄模拟)将甲、乙、丙、丁四名学生分到两个不同的班，每个班至少分到一名学生，且甲、乙两名学生不能分到同一个班，则不同的分法的种数为________(用数字作答)．解析：第1步，把甲、乙分到不同班级有A 22＝2种分法； 第2步，分丙、丁：①丙、丁分到同一班级有2种方法； ②丙、丁分到两个不同班有A 22＝2种分法．由分步乘法计数原理，不同的分法为2×(2＋2)＝8(种)． 答案：811．如图所示，在A ，B 间有四个焊接点，若焊接点脱落，则可能导致电路不通，今发现A ，B 之间线路不通，则焊接点脱落的不同情况有________种．解析：四个焊点共有24种情况，其中使线路通的情况有：1,4都通，2和3至少有一个通时线路才通，共有3种可能．故不通的情况有24－3＝13(种)可能．答案：1312.(2017·宁波调研)如图，用4种不同的颜色对图中5个区域涂色(4种颜色全部使用)，要求每个区域涂一种颜色，相邻的区域不能涂相同的颜色，则不同的涂色方法有________种．解析：若1,3不同色，则1,2,3,4必不同色，有3A 44＝72种涂色法；若1,3同色，有C 14C 13A 22＝24种涂色法．根据分类计数原理可知，共有72＋24＝96种涂色法．答案：96 三、解答题13．已知(a 2＋1)n展开式中的二项式系数之和等于⎝⎛⎭⎪⎫165x 2＋1x 5的展开式的常数项，而(a 2＋1)n的展开式的二项式系数最大的项等于54，求正数a 的值．解：⎝ ⎛⎭⎪⎫165x 2＋1x 5展开式的通项T r ＋1＝C r 5⎝⎛⎭⎪⎫165x 25－r ·⎝ ⎛⎭⎪⎫1x r ＝C r 5⎝ ⎛⎭⎪⎫1655－r x 20－5r2，令20－5r ＝0，得r ＝4， 故常数项T 5＝C 45·165＝16， 又(a 2＋1)n展开式的各项系数之和为2n， 由题意得2n＝16，∴n ＝4.∴(a 2＋1)4展开式中二项式系数最大的项是中间项T 3， 从而C 24(a 2)2＝54，∴a ＝ 3.14．从1到9的9个数字中取3个偶数4个奇数，试问：(1)能组成多少个没有重复数字的七位数？(2)上述七位数中，3个偶数排在一起的有几个？(3)(1)中的七位数中，偶数排在一起，奇数也排在一起的有几个？解：(1)分三步完成：第一步，在4个偶数中取3个，有C34种情况；第二步，在5个奇数中取4个，有C45种情况；第三步，3个偶数，4个奇数进行排列，有A77种情况．所以符合题意的七位数有C34C45A77＝100 800个．(2)上述七位数中，3个偶数排在一起的有C34C45A33A55＝14 400个．(3)(1)中的七位数中，3个偶数排在一起，4个奇数也排在一起的有C34C45A33A44A22＝5 760个．。

专题11.1 计数原理1.育英学校派出5名优秀教师去边远地区的三所中学进行教学交流，每所中学至少派一名教师，则不同的分配方法有________种．【答案】150【解析】分组法是（1,1,3），（1,2,2），共有113122543542222225C C C C C C A A +=,再分配，乘以33A ，即得总数150. 2. 只用1,2,3三个数字组成一个四位数，规定这三个数必须同时使用，且同一数字不能相邻出现，则这样的四位数有 ________个．【答案】183.各大学在高考录取时采取专业志愿优先的录取原则．一考生从某大学所给的7个专业中，选择3个作为自己的第一、二、三专业志愿，其中甲、乙两个专业不能同时兼报，则该考生有_____________种不同的填报专业志愿的方法（用数字作答）．【答案】180【解析】分三类情况讨论，一是选甲不选乙，有,3325A C 二是选乙不选甲，有,3325A C 三是既不选甲也不选乙,有,3335A C 所以共有+3325A C +3325A C .1803335=A C .4. 6名同学争夺3项冠军，获得冠军的可能性有 种.【答案】729【解析】根据分步乘法计数原理获得冠军的可能性有72933333336==⨯⨯⨯⨯⨯.5. 若a ，b∈N *，且a ＋b≤5，则复数a ＋bi 的个数为______．【答案】10【解析】按a 分类，当a 取1,2,3,4时，b 的值分别有4个、3个、2个、1个，由分类计数原理，得复数a ＋bi 共有4＋3＋2＋1＝10(个)．6. 如图，在A 、B 间有四个焊接点，若焊接点脱落，而可能导致电路不通，如今发现A 、B 之间线路不通，则焊接点脱落的不同情况有 ________．【答案】137.如图，用4种不同的颜色对图中5个区域涂色(4种颜色全部使用)，要求每个区域涂1种颜色，相邻的区域不能涂相同的颜色，则不同的涂色种数有________种．【答案】96【解析】若1,3不同色，则1,2,3,4必不同色，有344A ＝72种涂色法；若1,3同色，有14C 33A ＝24种涂色法．根据分类加法计数原理可知，共有72＋24＝96种涂色法．8从0，1，2，3，4，5这6个数字中任意取4个数字组成一个没有重复数字且能被3整除的四位数，这样的四位数有 个．【答案】96【解析】依题意，只需组成的四位数各位数字的和能被3整除．将这六个数字按照被3除的余数分类，共分为3类：{}0,3，{}1,4，{}2,5，若四位数含0，则另外3个数字为3、1,4之一、2,5之一，此时有11132233C C C A 72=种；若四位数不含0，则4个数字为1,2,4,5，此时有4424A =种，由分类计数原理，这样的四位数有722496+=个．9. 4张卡片的正、反面分别写有0与1,2与3,4与5,6与7，将其中3张卡片排放在一起，可组成________个不同的三位数．【答案】168【解析】要组成三位数，根据首位、十位、个位应分三步：第一步：首位可放8－1＝7(个)数；第二步：十位可放6个数；第三步：个位可放4个数．故由分步计数原理，得共可组成7×6×4＝168(个)不同的三位数．10.工人在安装一个正六边形零件时，需要固定如图所示的六个位置的螺丝，第一阶段，首先随意拧一个螺丝，接着拧它对角线上（距离它最远的，下同）螺丝，再随意拧第三个螺丝，第四个也拧它对角线上螺丝，第五个和第六个以此类推，但每个螺丝都不要拧死;第二阶段，将每个螺丝拧死，但不能连续拧相邻的2个螺丝。

计数原理(2018年4月)一、 知识要点1、分类计数原理(加法原理)：做一件事情，完成它可以有n 类办法，在第一类办法中有1m 种不同的方法，在第二类办法中有2m 种不同的方法，……，在第n 类办法中有n m 种不同的方法．那么完成这件事共有 12n N m m m =+++ 种不同的方法．2、分步计数原理(乘法原理)：做一件事情，完成它需要分成n 个步骤，做第一步有1m 种不同的方法，做第二步有2m 种不同的方法，……，做第n 步有n m 种不同的方法，那么完成这件事有12n N m m m =⨯⨯⨯ 种不同的方法．二、 例题精讲例 1 、电视台在“欢乐今宵”节目中拿出两个信箱，其中存放着先后两次竞猜中成绩优秀的观众来信，甲信箱中有30封，乙信箱中有20封现由主持人抽奖确定幸运观众，若先确定一名幸运之星，再从两信箱中各确定一名幸运伙伴，有多少种不同的结果？ 答案：28800．例2、从集合{1，2，3，…，10}中，选出由5个数组成的子集，使得这5个数中的任何两个数的和不等于11，这样的子集共有多少个?答案：32个例3、某城市在中心广场建造一个花圃，花圃分为6个部分（如下图）现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有_____________种．（以数字作答）答案：120种654321例4、（1）有红、黄、白色旗子各n 面（3n ），取其中一面、二面、三面组成纵列信号，可以有多少不同的信号？（2）有1元、5元、10元的钞票各一张，取其中一张或几张，能组成多少种不同的币值？答案：（1）60；（2）7种．例5、d c b a ,,,排成一行，其中a 不排第一，b 不排第二，c 不排第三，d 不排第四的不同排法共有多少种？答案：9种．例6、关于正整数2160，求：（1）它有多少个不同的正因数？（2）它的所有正因数的和是多少？答案：（1）40个；（2）7440．例7、如图所示,问从A 到D 每次不许走重复的路,共有多少种走法?(注:每次的路线一个地方只能经过一次)答案：16例8、由数字0，1，2，3，4，（1）可组成多少个没有重复数字且比20000大的自然数？（2）2不在千位，且4不在十位的五位数有多少个？答案：（1）72；（2）1600三、课堂练习1、4名男生和3名女生排成一行，按下列要求各有多少种排法：（1）男生必须排在一起；（2）女生互不相邻；（3）男女生相间；（4）女生按指定顺序排列．答案：576；1440；144；840.2、6本不同的书全部送给5人，每人至少1本，有种不同的送书方法．答案：18003、三名男歌手和两名女歌手联合举行一场演唱会,演出时要求两名女歌手之间恰有一名男歌手,则共有出场方案种．答案：364、圆周上有12个不同的点，过其中任意两点作弦，这些弦在圆内的交点个数最多是．答案：4955、7人站一排，甲不站排头，也不站排尾，不同的站法种数有种；甲不站排头，乙不站排尾，不同站法种数有种．答案：3600；3720.6、远洋轮一根旗杆上用红、蓝、白三面旗帜中，一面，二面或三面表示信号，则最多可组成不同信号有___________种．答案：15四、课后作业一、填空题1、十字路口来往的车辆，如果不允许回头，共有_________种行车路线．答案：122、从正方体的6个面中选取3个面，其中有2个面不相邻的选法共有种．答案：123、从1到10的正整数中，任意抽取两个相加，所得和为奇数的不同情形有______种．答案：254、72的正约数（包括1和72）共有__________个．答案：125、从－1，0，1，2这四个数中选三个不同的数作为函数()2f x ax bx c =++的系数，可组成不同的二次函数共有_____________个，其中不同的偶函数共有_____________个．（用数字作答）答案：18；66、如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色．现有4种颜色可供选择，则不同的着色方法共有_____________种．（以数字作答） 答案：72 二、选择题7、某城市的电话号码，由六位升为七位（首位数字均不为零），则该城市可增加的电话部数是( )A 、9×8×7×6×5×4×3B 、8×96C 、9×106D 、81×105答案：D8、从长度分别为1、2、3、4的四条线段中，任取三条的不同取法共有n 种在这些取法中，以取出的三条线段为边可组成的三角形的个数为m ，则n m 等于( ) A 、0 B 、41 C 、21 D 、43 答案：B9、某班新年联欢会原定的6个节目已排成节目单，开演前又增加了3个新节目，如果将这3个节目插入节目单中，那么不同的插法种数为( )A 、504B 、210C 、336D 、120答案：A三、解答题10、在所有两位数中，个位数字大于十位数字的两位数共有多少个？答案：3611、五名学生报名参加四项体育比赛，每人限报一项，报名方法的种数为多少？又他们争夺这四项比赛的冠军，获得冠军的可能性有多少种？答案：（1）1024种；（2）526种．12、三边长均为整数，且最大边长为11的三角形的个数是多少？答案：36⑤④③②①。

计数原理一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．用数字1，2，3，4，5可以组成没有重复数字，并且比20000大的五位偶数共有( )A ．48个B ．36个C ．24个D ．18个 【答案】B2．在()103x -的展开式中，6x 的系数为( )A ．610C 27- B ．410C 27 C ．610C 9-D ．410C 9【答案】D3．若直角坐标平面内A 、B 两点满足条件：①点A 、B 都在f(x)的图象上；②点A 、B 关于原点对称，则对称点对(A ，B)是函数的一个“姊妹点对”(点对(A ，B)与（B ，A ）可看作一个“姊妹点对”). 已知函数 f(x)=⎪⎩⎪⎨⎧≥<+02022x e x xx x，则f(x)的“姊妹点对”有( )个A ．1B ．3C ．2D ．4【答案】C4．101x x ⎛⎫+ ⎪⎝⎭展开式中的常数项为( )A ．第5项B ．第6项C ．第5项或第6项D ．不存在【答案】B5．已知集合A=｛5｝,B=｛1,2｝,C=｛1,3,4｝，从这三个集合中各取一个元素构成空间直角坐标系中点的坐标，则确定的不同点的个数为( )A.33B.34C.35D.36 【答案】A 6．若n展开式中存在常数项，则n 的最小值为( ) A ．５ B ．６ C ．７ D ．８ 【答案】A7．某飞机显示屏上的每个指示灯均以红光或蓝光来表示不同的信号，已知一排有8个指示灯．若每次显示其中的4个，并且恰有3个相邻，则可显示的不同信号共有 ( ） A ．80种 B ．160种 C ．320种 D ．640种 【答案】C8．如果一条直线与一个平面垂直，那么，称此直线与平面构成一个“正交线面对”．在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( ) A ．48 B ．18 C ．24 D ．36 【答案】D9．我们把可表示为两个连续正奇数的平方差的正整数称为“和谐数”，则在集合{}2013,,3,2,1 中，共有“和谐数”的个数是( ) A ．502 B ．503 C ．251 D ．252 【答案】C10．某电视台连续播放5个不同的广告，其中有3个不同的商业广告和2个不同的奥运宣传广告，要求最后播放的必须是奥运宣传广告，且两个奥运宣传广告不能连续播放，则不同的播放方式有( ) A ．120种 B ．48种 C ．36种 D ．18种 【答案】C11．已知点),(y x P ，其中{}2,1∈x ，{}4,3,1∈y ，则在同一直角坐标系中所确定的不同点的个数是( )A ．6B ．12C ．8D ．5 【答案】A12．从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动，每人一天，要求星期五有一人参加，星期六有两人参加，星期日有一人参加，则不同的选派方法共有( ) A ．120种 B ．96种 C ．60种 D ．48种 【答案】C二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．若()44104x a x a a 3x 2+⋅⋅⋅++=+，则()()2312420a a a a a +-++的值为 ．【答案】114．6名运动员比赛前将外衣放在休息室，比赛后都回到休息室取衣服，由于灯光暗淡，有一部分队员拿错了外衣，其中只有2人拿到自己的外衣，且另外的4人拿到别人的外衣情况个数为 . 【答案】13515．6人站成一排，甲、乙、丙3个人不能都站在一起的排法种数为 ． 【答案】576种16．2012年3月10日是第七届世界肾脏日，某社区服务站将5位志愿者分成3组，其中两组各2人，另一组1人，分别去三个不同的社区宣传这届肾脏日的主题：“保护肾脏，拯救心脏”，不同的分配方案有 种．(用数字作答) 【答案】90三、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤) 17．已知n n x x f )1()(+=，n ∈N *.(1) 若)(3)(2)()(654x f x f x f x g ++=，求)(x g 中含2x 项的系数；(2) 若n p 是)(x f n 展开式中所有无理项的系数和，数列}{n a 是各项都大于1的数组成的数列，试用数学归纳法证明：n p )1(21+n a a a ≥(1＋1a )(1＋2a )…(1＋n a )． 【答案】(1) g(x)中含x 2项的系数为C 44＋2C 45＋3C 46＝1＋10＋45＝56.(2) 证明：由题意，p n ＝2n －1.① 当n ＝1时，p 1(a 1＋1)＝a 1＋1，成立；② 假设当n ＝k 时，p k (a 1a 2…a k ＋1)≥(1＋a 1)(1＋a 2)…(1＋a k )成立， 当n ＝k ＋1时，(1＋a 1)(1＋a 2)…(1＋a k )(1＋a k ＋1)≤2k －1(a 1a 2…a k ＋1)(1＋a k ＋1) ＝2k －1(a 1a 2…a k a k ＋1＋a 1a 2…a k ＋a k ＋1＋1)．(*)∵ a k ＞1，a 1a 2…a k (a k ＋1－1)≥a k ＋1－1，即a 1a 2…a k a k ＋1＋1≥a 1a 2…a k ＋a k ＋1，代入(*)式得(1＋a 1)(1＋a 2)…(1＋a k )(1＋a k ＋1)≤2k(a 1a 2…a k a k ＋1＋1)成立．综合①②可知，p n （a 1a 2…a n ＋1）≥（1＋a 1）（1＋a 2）…（1＋a n ）对任意n ∈N *成立．18．有9名学生，其中2名会下象棋但不会下围棋，3名会下围棋但不会下象棋，4名既会下围棋又会下象棋；现在要从这9名学生中选出2名学生，一名参加象棋比赛，另一名参加围棋比赛，共有多少种不同的选派方法？【答案】设2名会下象棋但不会下围棋的同学组成集合A ，3名会下围棋但不会下象棋的同学组成集合B ，4名既会下围棋又会下象棋的同学组成集合C ，则选派2名参赛同学的方法可以分为以下4类： 第一类：A 中选1人参加象棋比赛，B 中选1人参加围棋比赛，方法数为61312=⋅C C 种；第二类：C 中选1人参加象棋比赛，B 中选1人参加围棋比赛，方法数为121314=⋅C C 种；第三类：C 中选1人参加围棋比赛，A 中选1人参加象棋比赛，方法数为81214=⋅C C 种； 第四类：C 中选2人分别参加两项比赛，方法数为1224=A 种；由分类加法计数原理，选派方法数共有：6+12+8+12=38种。

第十一章⎪⎪⎪ 计数原理、概率、随机变量及其分布列第一节排列、组合突破点(一) 两个计数原理1．分类加法计数原理完成一件事有两类不同方案，在第1类方案中有m 种不同的方法，在第2类方案中有n 种不同的方法，那么完成这件事共有N ＝m ＋n 种不同的方法．2．分步乘法计数原理完成一件事需要两个步骤，做第1步有m 种不同的方法，做第2步有n 种不同的方法，那么完成这件事共有N ＝m ×n 种不同的方法．3．两个计数原理的比较能用分类加法计数原理解决的问题具有以下特点：(1)完成一件事有若干种方法，这些方法可以分成n 类．本节主要包括2个知识点：1.两个计数原理；排列、组合问题.(2)用每一类中的每一种方法都可以完成这件事．(3)把各类的方法数相加，就可以得到完成这件事的所有方法数．[例1] (1)在所有的两位数中，个位数字大于十位数字的两位数共有________个．(2)如图，从A 到O 有________种不同的走法(不重复过一点)．(3)若椭圆x 2m ＋y 2n＝1的焦点在y 轴上，且m ∈{1,2,3,4,5}，n ∈{1,2,3,4,5,6,7}，则这样的椭圆的个数为________．[解析] (1)法一：按个位数字分类，个位可为2,3,4,5,6,7,8,9，共分成8类，在每一类中满足条件的两位数分别有1个，2个，3个，4个，5个，6个，7个，8个，则共有1＋2＋3＋4＋5＋6＋7＋8＝36个两位数．法二：按十位数字分类，十位可为1,2,3,4,5,6,7,8，共分成8类，在每一类中满足条件的两位数分别有8个，7个，6个，5个，4个，3个，2个，1个，则共有8＋7＋6＋5＋4＋3＋2＋1＝36个两位数．(2)分3类：第一类，直接由A 到O ，有1种走法；第二类，中间过一个点，有A →B →O 和A →C →O 2种不同的走法；第三类，中间过两个点，有A →B →C →O 和A →C →B →O 2种不同的走法．由分类加法计数原理可得共有1＋2＋2＝5种不同的走法．(3)当m ＝1时，n ＝2,3,4,5,6,7，共6个；当m ＝2时，n ＝3,4,5,6,7，共5个；当m ＝3时，n ＝4,5,6,7，共4个；当m ＝4时，n ＝5,6,7，共3个；当m ＝5时，n ＝6,7，共2个．故共有6＋5＋4＋3＋2＝20个满足条件的椭圆．[答案] (1)36 (2)5 (3)20[易错提醒](1)根据问题的特点确定一个合适的分类标准，分类标准要统一，不能遗漏．(2)分类时，注意完成这件事的任何一种方法必须属于某一类，不能重复．分步乘法计数原理(1)完成一件事需要经过n 个步骤，缺一不可．(2)完成每一步有若干种方法．(3)把各个步骤的方法数相乘，就可以得到完成这件事的所有方法数．[例2] (1)从－1,0,1,2这四个数中选三个数作为函数f (x )＝ax 2＋bx ＋c 的系数，则可组成________个不同的二次函数，其中偶函数有________个(用数字作答)．(2)如图，某电子器件由3个电阻串联而成，形成回路，其中有6个焊接点A，B，C，D，E，F，如果焊接点脱落，整个电路就会不通．现发现电路不通，那么焊接点脱落的可能情况共有________种．[解析](1)一个二次函数对应着a，b，c(a≠0)的一组取值，a的取法有3种，b的取法有3种，c的取法有2种，由分步乘法计数原理知共有3×3×2＝18个二次函数．若二次函数为偶函数，则b＝0，同理可知共有3×2＝6个偶函数．(2)因为每个焊接点都有脱落与未脱落两种情况，而只要有一个焊接点脱落，则电路就不通，故共有26－1＝63种可能情况．[答案(1)186(2)63[易错提醒](1)利用分步乘法计数原理解决问题时要注意按事件发生的过程来合理分步，即分步是有先后顺序的，并且分步必须满足：完成一件事的各个步骤是相互依存的，只有各个步骤都完成了，才算完成这件事．(2)谨记分步必须满足的两个条件：一是各步骤互相独立，互不干扰；二是步与步确保连续，逐步完成．两个计数原理的综合问题数原理，即分类时，每类的方法可能要运用分步完成，而分步时，每步的方法数可能会采取分类的思想求解．分类的关键在于做到“不重不漏”，分步的关键在于正确设计分步的程序，即合理分类，准确分步．[例3](1)用数字0,1,2,3,4,5组成没有重复数字的五位数，其中比40 000大的偶数共有()A．144个B．120个C．96个D．72个(2)某班一天上午有4节课，每节都需要安排1名教师去上课，现从A，B，C，D，E，F 6名教师中安排4人分别上一节课，第一节课只能从A、B两人中安排一个，第四节课只能从A、C两人中安排一人，则不同的安排方案共有________种．(3)如图，矩形的对角线把矩形分成A，B，C，D四部分，现用5种不同颜色给四部分涂色，每部分涂1种颜色，要求共边的两部分颜色互异，则共有________种不同的涂色方法．[解析](1)由题意可知，符合条件的五位数的万位数字是4或5.当万位数字为4时，个位数字从0,2中任选一个，共有2×4×3×2＝48个偶数；当万位数字为5时，个位数字从0,2,4中任选一个，共有3×4×3×2＝72个偶数．故符合条件的偶数共有48＋72＝120(个)．(2)①第一节课若安排A，则第四节课只能安排C，第二节课从剩余4人中任选1人，第三节课从剩余3人中任选1人，共有4×3＝12种安排方案．②第一节课若安排B，则第四节课可由A或C上，第二节课从剩余4人中任选1人，第三节课从剩余3人中任选1人，共有2×4×3＝24种安排方案．因此不同的安排方案共有12＋24＝36(种)．(3)区域A有5种涂色方法，区域B有4种涂色方法，区域C的涂色方法可分2类：若C与A涂同色，区域D有4种涂色方法；若C与A涂不同色，此时区域C有3种涂色方法，区域D也有3种涂色方法．所以共有5×4×1×4＋5×4×3×3＝260种涂色方法．[答案(1)B(2)36(3)260[方法技巧]使用两个计数原理进行计数的基本思想对需用两个计数原理解决的综合问题要“先分类，再分步”，即先分为若干个“既不重复也不遗漏”的类，再对每类中的计数问题分成若干个“完整的步骤”，求出每个步骤的方法数，按照分步乘法计数原理计算各类中的方法数，最后再按照分类加法计数原理得出总数．能力练通抓应用体验的“得”与“失”1．[考点二]某班新年联欢会原定的6个节目已排成节目单，开演前又增加了3个新节目，如果将这3个新节目插入节目单中，那么不同的插法种数为()A．504B．210C．336D．120解析：选A分三步，先插一个新节目，有7种方法，再插第二个新节目，有8种方法，最后插第三个节目，有9种方法．故共有7×8×9＝504种不同的插法．2．[考点二]教学大楼共有五层，每层均有两个楼梯，由一层到五层的走法有() A．10种B．25种C．52种D．24种解析：选D由一层到二层、由二层到三层、由三层到四层、由四层到五层各有2种走法，故共有2×2×2×2＝24种不同的走法．3．[考点一]已知两条异面直线a，b上分别有5个点和8个点，则这13个点可以确定不同的平面个数为()A．40 B．16 C．13 D．10解析：选C分两类情况讨论：第1类，直线a分别与直线b上的8个点可以确定8个不同的平面；第2类，直线b分别与直线a上的5个点可以确定5个不同的平面．根据分类加法计数原理知，共可以确定8＋5＝13个不同的平面．4．[考点一]我们把各位数字之和为6的四位数称为“六合数”(如2 013是“六合数”)，则“六合数”中首位为2的“六合数”共有()A．18个B．15个C．12个D．9个解析：选B依题意知，这个四位数的百位数、十位数、个位数之和为4.由4,0,0组成3个数，分别为400,040,004；由3,1,0组成6个数，分别为310,301,130,103,013,031；由2,2,0组成3个数，分别为220,202,022；由2,1,1组成3个数，分别为211,121,112.共计3＋6＋3＋3＝15个“六合数”．5.[考点三]如图，用4种不同的颜色对图中5个区域涂色(4种颜色全部使用)，要求每个区域涂一种颜色，相邻的区域不能涂相同的颜色，则不同的涂色方法有________种．解析：按区域1与3①区域1与3同色：先涂区域1与3，有4种方法，再涂区域2,4,5(还有3种颜色)，有3×2×1＝6种方法．所以区域1与3涂同色时，共有4×6＝24种方法．②区域1与3不同色：先涂区域1与3，有4×3＝12种方法，第二步，涂区域2有2种涂色方法，第三步，涂区域4只有一种方法，第四步，涂区域5有3种方法．所以这时共有12×2×1×3＝72种方法．故由分类加法计数原理，不同的涂色方法的种数为24＋72＝96.答案：966．[考点三]有A，B，C型高级电脑各一台，甲、乙、丙、丁4个操作人员的技术等级不同，甲、乙会操作三种型号的电脑，丙不会操作C型电脑，而丁只会操作A型电脑．从这4个操作人员中选3人分别去操作这三种型号的电脑，则不同的选派方法有________种(用数字作答)．解析：由于丙、丁两位操作人员的技术问题，要完成“从4个操作人员中选3人去操作这三种型号的电脑”这件事，则甲、乙两人至少要选派一人，可分四类：第1类，选甲、乙、丙3人，由于丙不会操作C型电脑，分2步安排这3人操作的电脑的型号，有2×2＝4种方法；第2类，选甲、乙、丁3人，由于丁只会操作A型电脑，这时安排3人分别去操作这三种型号的电脑，有2种方法；第3类，选甲、丙、丁3人，这时安排3人分别去操作这三种型号的电脑，只有1种方法；第4类，选乙、丙、丁3人，同样也只有1种方法．根据分类加法计数原理，共有4＋2＋1＋1＝8种选派方法．答案：8突破点(二)排列、组合问题1．排列与排列数(1)排列：从n个不同元素中取出m(m≤n)个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列．(2)排列数：从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数叫做从n个不同元素中取出m个元素的排列数，记作A m n.2．组合与组合数(1)组合：从n个不同元素中取出m(m≤n)个元素合成一组，叫做从n个不同元素中取出m个元素的一个组合．(2)组合数：从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数，叫做从n 个不同元素中取出m个元素的组合数，记作C m n.3．排列数、组合数的公式及性质4．排列与组合的比较解决排列问题的主要方法(1)解决“在”与“不在”的有限制条件的排列问题，既可以从元素入手，也可以从位置入手，原则是谁“特殊”谁优先．不管是从元素考虑还是从位置考虑，都要贯彻到底，不能既考虑元素又考虑位置．(2)解决相邻问题的方法是“捆绑法”，即把相邻元素看做一个整体和其他元素一起排列，同时要注意捆绑元素的内部排列．(3)解决不相邻问题的方法是“插空法”，即先考虑不受限制的元素的排列，再将不相邻的元素插在前面元素排列的空当中．(4)对于定序问题，可先不考虑顺序限制，排列后，再除以定序元素的全排列．(5)若某些问题从正面考虑比较复杂，可从其反面入手，即采用“间接法”．[例1](1)用0到9这10个数字，可以组成没有重复数字的三位偶数的个数为() A．324 B．648 C．328 D．360(2)市内某公共汽车站有6个候车位(成一排)，现有3名乘客随便坐在某个座位上候车，则恰好有2个连续空座位的候车方式的种数为()A．48 B．54 C．72 D．84(3)用1,2,3,4这四个数字组成无重复数字的四位数，其中恰有一个偶数夹在两个奇数之间的四位数的个数为________．[解析](1)首先应考虑是否含“0”．当含有0，且0排在个位时，有A29＝9×8＝72个三位偶数，当0排在十位时，有A14A18＝4×8＝32个三位偶数．当不含0时，有A14·A28＝4×8×7＝224个三位偶数．由分类加法计数原理，得符合题意的偶数共有72＋32＋224＝328(个)．(2)先把3名乘客进行全排列，有A33＝6种排法，排好后，有4个空，再将1个空位和余下的2个连续的空位插入4个空中，有A24＝12种排法，则共有6×12＝72种候车方式．(3)首先排两个奇数1,3，有A22种排法，再在2,4中取一个数放在1,3排列之间，有C12种排法，然后把这3个数作为一个整体与剩下的另一个偶数全排列，有A22种排法，即满足条件的四位数的个数为A22C12A22＝8.[答案](1)C(2)C(3)8组合问题组合问题的常见题型及解题思路(1)常见题型：一般有选派问题、抽样问题、图形问题、集合问题、分组问题等．(2)解题思路：①分清问题是否为组合问题；②对较复杂的组合问题，要搞清是“分类”还是“分步”，一般是先整体分类，然后局部分步，将复杂问题通过两个计数原理化归为简单问题．[例2](1)某学校为了迎接市春季运动会，从5名男生和4名女生组成的田径运动队中选出4人参加比赛，要求男、女生都有，则男生甲与女生乙至少有1人入选的方法种数为()A．85 B．86 C．91 D．90(2)若从1,2,3，…，9这9个整数中同时取4个不同的数，其和为偶数，则不同的取法的种数是()A．60 B．63 C．65 D．66(3)现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张．从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多1张，不同取法的种数为________．[解析](1)法一(直接法)：由题意，可分三类考虑：第1类，男生甲入选，女生乙不入选的方法种数为：C13C24＋C23C14＋C33＝31；第2类，男生甲不入选，女生乙入选的方法种数为：C14C23＋C24C13＋C34＝34；第3类，男生甲入选，女生乙入选的方法种数为：C23＋C14C13＋C24＝21.所以男生甲与女生乙至少有1人入选的方法种数为31＋34＋21＝86.法二(间接法)：从5名男生和4名女生中任意选出4人，男、女生都有的选法有C49－C45－C44＝120种；男、女生都有，且男生甲与女生乙都没有入选的方法有C47－C44＝34种．所以男生甲与女生乙至少有1人入选的方法种数为120－34＝86.(2)因为1,2,3，…，9中共有4个不同的偶数和5个不同的奇数，要使取出的4个不同的数的和为偶数，则4个数全为奇数，或全为偶数，或2个奇数和2个偶数，故有C45＋C44＋C25C24＝66种不同的取法．(3)第一类，含有1张红色卡片，不同的取法有C14C212＝264(种)．第二类，不含有红色卡片，不同的取法有C312－3C34＝220－12＝208(种)．由分类加法计数原理知，不同的取法共有264＋208＝472(种)．[答案(1)B(2)D(3)472[方法技巧]有限制条件的组合问题的解法组合问题的限制条件主要体现在取出元素中“含”或“不含”某些元素，或者“至少”或“最多”含有几个元素： (1)“含有”或“不含有”某些元素的组合题型．“含”，则先将这些元素取出，再由另外元素补足；“不含”，则先将这些元素剔除，再从剩下的元素中去选取．(2)“至少”或“最多”含有几个元素的题型．考虑逆向思维，用间接法处理．分组分配问题分组分配问题是排列、组合问题的综合运用，解决这类问题的一个基本指导思想就是先分组后分配．关于分组问题，有整体均分、部分均分和不等分三种，无论分成几组，都应注意只要有一些组中元素的个数相等，就存在均分现象．[例3] (1)教育部为了发展贫困地区教育，在全国重点师范大学免费培养教育专业师范生，毕业后要分到相应的地区任教．现有6个免费培养的教育专业师范毕业生要平均分到3所学校去任教，有________种不同的分派方法．(2)某科室派出4名调研员到3个学校，调研该校高三复习备考近况，要求每个学校至少一名，则不同的分配方案种数为________．(3)若将6名教师分到3所中学任教，一所1名，一所2名，一所3名，则有________种不同的分法．[解析] (1)先把6个毕业生平均分成3组，有C 26C 24C 22A 33种方法，再将3组毕业生分到3所学校，有A 33＝6种方法，故将6个毕业生平均分到3所学校，共有C 26C 24C 22A 33·A 33＝90种不同的分派方法．(2)分两步完成：第一步，将4名调研员按2,1,1分成三组，其分法有C 24C 12C 11A 22种；第二步，将分好的三组分配到3个学校，其分法有A 33种，所以满足条件的分配方案有C 24C 12C 11A 22·A 33＝36种．(3)将6名教师分组，分三步完成： 第1步，在6名教师中任取1名作为一组，有C 16种分法；第2步，在余下的5名教师中任取2名作为一组，有C 25种分法；第3步，余下的3名教师作为一组，有C 33种分法．根据分步乘法计数原理，共有C 16C 25C 33＝60种分法．再将这3组教师分配到3所中学，有A 33＝6种分法，故共有60×6＝360种不同的分法．[答案 (1)90 (2)36 (3)360[方法技巧] 分组分配问题的三种类型及求解策略能力练通 抓应用体验的“得”与“失”1．[考点一]A ，B ，C ，D ，E ，F 六人围坐在一张圆桌周围开会，A 是会议的中心发言人，必须坐在最北面的椅子上，B ，C 二人必须坐相邻的两把椅子，其余三人坐剩余的三把椅子，则不同的座次有( )A ．60种B ．48种C ．30种D ．24种解析：选B 由题知，可先将B ，C 二人看作一个整体，再与剩余人进行排列，则不同的座次有A 22A 44＝48种．2．[考点一]有5列火车分别准备停在某车站并行的5条轨道上，若快车A 不能停在第3道上，货车B 不能停在第1道上，则5列火车不同的停靠方法数为( )A ．56B ．63C ．72D ．78解析：选D 若没有限制，5列火车可以随便停，则有A 55种不同的停靠方法；快车A停在第3道上，则5列火车不同的停靠方法为A 44种；货车B 停在第1道上，则5列火车不同的停靠方法为A 44种；快车A 停在第3道上，且货车B 停在第1道上，则5列火车不同的停靠方法为A 33种．故符合要求的5列火车不同的停靠方法数为A 55－2A 44＋A 33＝120－48＋6＝78.3．[考点三]某局安排3名副局长带5名职工去3地调研，每地至少去1名副局长和1名职工，则不同的安排方法总数为( )A ．1 800B ．900C ．300D ．1 440解析：选B 分三步：第一步，将5名职工分成3组，每组至少1人，则有⎝⎛⎭⎫C 35C 12C 11A 22＋C 15C 24C 22A 22种不同的分组方法；第二步，将这3组职工分到3地有A 33种不同的方法；第三步，将3名副局长分到3地有A 33种不同的方法．根据分步乘法计数原理，不同的安排方案共有⎝⎛⎭⎫C 35C 12C 11A 22＋C 15C 24C 22A 22·A 33A 33＝900(种)，故选B.4．[考点二]如图所示，要使电路接通，则5个开关不同的开闭方式有________种．解析：当第一组开关有一个接通时，电路接通有C12·(C13＋C23＋C33)＝14种方式；当第一组两个都接通时，电路接通有C22(C13＋C23＋C33)＝7种方式，所以共有14＋7＝21种方式．答案：215．[考点二]有9名学生，其中2名会下象棋但不会下围棋，3名会下围棋但不会下象棋，4名既会下围棋又会下象棋；现在要从这9名学生中选出2名学生，一名参加象棋比赛，另一名参加围棋比赛，共有________种不同的选派方法．解析：设2名会下象棋但不会下围棋的同学组成集合A,3名会下围棋但不会下象棋的同学组成集合B,4名既会下围棋又会下象棋的同学组成集合C，则选派2名参赛同学的方法可以分为以下4类：第一类：A中选1人参加象棋比赛，B中选1人参加围棋比赛，选派方法为C12·C13＝6种；第二类：C中选1人参加象棋比赛，B中选1人参加围棋比赛，选派方法为C14·C13＝12种；第三类：C中选1人参加围棋比赛，A中选1人参加象棋比赛，选派方法为C14·C12＝8种；第四类：C中选2人分别参加两项比赛，选派方法为A24＝12种；由分类加法计数原理，不同的选派方法共有6＋12＋8＋12＝38(种)．答案：38[全国卷5年真题集中演练——明规律]1．(2016·全国甲卷)如图，小明从街道的E处出发，先到F处与小红会合，再一起到位于G处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为()A．24 B．18 C．12 D．9解析：选B分两步：第一步，从E→F，有6条可以选择的最短路径；第二步，从F→G，有3条可以选择的最短路径．由分步乘法计数原理可知有6×3＝18条可以选择的最短路径．故选B.2．(2016·全国丙卷)定义“规范01数列”{a n}如下：{a n}共有2m项，其中m项为0，m项为1，且对任意k≤2m，a1，a2，…a k中0的个数不少于1的个数，若m＝4，则不同的“规范01数列”共有()A．18个B．16个C．14个D．12个解析：选C当m＝4时，数列{a n}共有8项，其中4项为0,4项为1，要满足对任意k≤8，a1，a2，…a k中0的个数不少于1的个数，则必有a1＝0，a8＝1，a2可为0，也可为1.(1)当a2＝0时，分以下3种情况：①若a3＝0，则a4，a5，a6，a7中任意一个为0均可，则有C14＝4种情况；②若a3＝1，a4＝0，则a5，a6，a7中任意一个为0均可，有C13＝3种情况；③若a3＝1，a4＝1，则a5必为0，a6，a7中任意一个为0均可，有C12＝2种情况；(2)当a2＝1时，必有a3＝0，分以下2种情况：①若a4＝0，则a5，a6，a7中任一个为0均可，有C13＝3种情况；②若a4＝1，则a5必为0，a6，a7中任一个为0均可，有C12＝2种情况．综上所述，不同的“规范01数列”共有4＋3＋2＋3＋2＝14个，故选C.3．(2012·新课标全国卷)将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有() A．12种B．10种C．9种D．8种解析：选A2名教师各在1个小组，给其中1名教师选2名学生，有C24种选法，另2名学生分配给另1名教师，然后将2个小组安排到甲、乙两地，有A22种方案，故不同的安排方案共有C24A22＝12种，选A.[课时达标检测] 重点保分课时——一练小题夯双基，二练题点过高考[练基础小题——强化运算能力]1．(2016·四川高考)用数字1,2,3,4,5组成没有重复数字的五位数，其中奇数的个数为()A．24 B．48C．60 D．72解析：选D奇数的个数为C13A44＝72.2．世界华商大会的某分会场有A，B，C三个展台，将甲、乙、丙、丁共4名“双语”志愿者分配到这三个展台，每个展台至少1人，其中甲、乙两人被分配到同一展台的不同分法的种数有()A．12种B．10种C．8种D．6种解析：选D因为甲、乙两人被分配到同一展台，所以可以把甲与乙捆在一起，看成一个人，然后将3个人分到3个展台上进行全排列，即有A33种分配方法，所以甲、乙两人被分配到同一展台的不同分法的种数有A33＝6种．3．在1,2,3,4,5这五个数字组成的没有重复数字的三位数中，各位数字之和为奇数的共有()A．36个B．24个C．18个D．6个解析：选B各位数字之和是奇数，则这三个数字中三个都是奇数或两个偶数一个奇数，所以符合条作的三位数有A33＋C13A33＝6＋18＝24(个)．4.如图所示的几何体由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成，现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色)，要求相邻的面均不同色，则不同的染色方案共有________种．解析：先涂三棱锥P-ABC的三个侧面，然后涂三棱柱ABC-A1B1C1的三个侧面，共有3×2×1×2＝12种不同的涂色方案．答案：12[练常考题点——检验高考能力]一、选择题1．从2,3,4,5,6,7,8,9这8个数中任取2个不同的数分别作为一个对数的底数和真数，则可以组成不同对数值的个数为()A．56 B．54C．53 D．52解析：选D在8个数中任取2个不同的数可以组成A28＝56个对数值；但在这56个对数值中，log24＝log39，log42＝log93，log23＝log49，log32＝log94，即满足条件的对数值共有56－4＝52(个)．2．如图所示，在A、B间有四个焊接点1,2,3,4，若焊接点脱落导致断路，则电路不通．今发现A，B之间电路不通，则焊接点脱落的不同情况有()A．9种B．11种C．13种D．15种解析：选C按照焊接点脱落的个数进行分类．若脱落1个，则有(1)，(4)，共2种情况；若脱落2个，有(1,4)，(2,3)，(1,2)，(1,3)，(4,2)，(4,3)，共6种情况；若脱落3个，有(1,2,3)，(1,2,4)，(2,3,4)，(1,3,4)，共4种情况；若脱落4个，有(1,2,3,4)，共1种情况．综上共有2＋6＋4＋1＝13种焊接点脱落的情况．3．现有2门不同的考试要安排在5天之内进行，每天最多进行一门考试，且不能连续两天有考试，那么不同的考试安排方案种数是( )A ．12B ．6C ．8D ．16解析：选A 若第一门安排在开头或结尾，则第二门有3种安排方法，这时共有C 12×3＝6种安排方案；若第一门安排在中间的3天中，则第二门有2种安排方法，这时共有C 13×2＝6种安排方案．综上可得，不同的考试安排方案共有6＋6＝12(种)．4．有5本不同的教科书，其中语文书2本，数学书2本，物理书1本．若将其并排摆放在书架的同一层上，则同一科目书都不相邻的放法种数是( )A ．24B ．48C ．72D ．96解析：选B 据题意可先摆放2本语文书，当1本物理书在2本语文书之间时，只需将2本数学书插在前3本书形成的4个空中即可，此时共有A 22A 24种摆放方法；当1本物理书放在2本语文书一侧时，共有A 22A 12C 12C 13种不同的摆放方法，由分类加法计数原理可得共有A 22A 24＋A 22A 12C 12C 13＝48种摆放方法．5．“住房”“医疗”“教育”“养老”“就业”成为现今社会关注的五个焦点．小赵想利用国庆节假期调查一下社会对这些热点的关注度．若小赵准备按照顺序分别调查其中的4个热点，则“住房”作为其中的一个调查热点，但不作为第一个调查热点的种数为( )A ．13B ．24C ．18D ．72解析：选D 可分三步：第一步，先从“医疗”“教育”“养老”“就业”这4个热点中选出3个，有C 34种不同的选法；第二步， 在调查时，“住房”安排的顺序有A 13种可能情况；第三步，其余3个热点调查的顺序有A 33种排法．根据分步乘法计数原理可得，不同调查顺序的种数为C 34A 13A 33＝72.6．将A ，B ，C ，D ，E 排成一列，要求A ，B ，C 在排列中顺序为“A ，B ，C ”或“C ，B ，A ”(可以不相邻)，这样的排列数有( )A ．12种B ．20种C ．40种D ．60种解析：选C 五个元素没有限制全排列数为A 55，由于要求A ，B ，C 的次序一定(按A ，B ，C 或C ，B ，A )，故除以这三个元素的全排列A 33，可得这样的排列数有A 55A 33×2＝40种．二、填空题7．某班组织文艺晚会，准备从A ，B 等 8 个节目中选出 4 个节目演出，要求A ，B 两个节目至少有一个选中，且A ，B 同时选中时，它们的演出顺序不能相邻，那么不同演出顺序的种数为________．解析：当A，B节目中只选其中一个时，共有C12C36A44＝960 种演出顺序；当A，B节目都被选中时，由插空法得共有C26A22A23＝180 种演出顺序，所以一共有1 140种演出顺序．答案：1 1408．4位同学参加某种形式的竞赛，竞赛规则规定：选甲题答对得100分，答错得－100分，选乙题答对得90分，答错得－90分，若4位同学的总分为0分，则这4位同学不同得分情况的种数是________．解析：由于4位同学的总分为0分，故4位同学选甲、乙题的人数有且只有三种情况：①甲：4人，乙：0人；②甲：2人，乙：2人；③甲：0人，乙：4人．对于①，需2人答对，2人答错，共有C24＝6种情况；对于②，选甲题的需1人答对，1人答错，选乙题的也如此，有C24C12C12＝24种情况；对于③，与①相同，有6种情况，故共有6＋24＋6＝36种不同的得分情况．答案：369．把座位编号为1,2,3,4,5的五张电影票全部分给甲、乙、丙、丁四个人，每人至少一张，至多两张，且分得的两张票必须是连号，那么不同的分法种数为________(用数字作答)．解析：先将票分为符合条件的4份，由题意，4人分5张票，且每人至少一张，至多两张，则三人每人一张，一人2张，且分得的票必须是连号，相当于将1,2,3,4,5这五个数用3个板子隔开，分为四部分且不存在三连号．在4个空位插3个板子，共有C34＝4种情况，再对应到4个人，有A44＝24种情况，则共有4×24＝96种不同分法．答案：9610．有红、蓝、黄、绿四种颜色的球各6个，每种颜色的6个球分别标有数字1,2,3,4,5,6，从中任取3个标号不同的球，这3个球颜色互不相同且所标数字互不相邻的取法种数为________．解析：所标数字互不相邻的取法有135,136,146,246，共4种.3个球颜色互不相同有A34＝4×3×2＝24种取法，所以这3个球颜色互不相同且所标数字互不相邻的取法有4×24＝96(种)．答案：96三、解答题11．有5个男生和3个女生，从中选出5人担任5门不同学科的科代表，求分别符合下列条件的选法数：(1)有女生但人数必须少于男生；(2)某女生一定担任语文科代表；(3)某男生必须包括在内，但不担任数学科代表；(4)某女生一定要担任语文科代表，某男生必须担任科代表，但不担任数学科代表．。

第十三章计数原理考点1 排列与组合1.(2016·全国Ⅱ，5)如图，小明从街道的E处出发，先到F处与小红会合，再一起到位于G处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为()A.24B.18C.12D.91.B [从E点到F点的最短路径有6种，从F点到G点的最短路径有3种，所以从E点到G 点的最短路径为6×3＝18种，故选B.]2.(2016·全国Ⅲ，12)定义“规范01数列”{a n}如下：{a n}共有2m项，其中m项为0，m项为1，且对任意k≤2m，a1，a2，…，a k中0的个数不少于1的个数.若m＝4，则不同的“规范01数列”共有()A.18个B.16个C.14个D.12个2.C [第一位为0，最后一位为1，中间3个0，3个1，三个1在一起时为000111，001110；只有2个1相邻时，共A24种，其中110100；110010；110001，101100不符合题意，三个1都不在一起时有C34种，共2＋8＋4＝14.]3.(2016·四川，4)用数字1，2，3，4，5组成没有重复数字的五位数，其中奇数的个数为()A.24B.48C.60D.723.D [由题可知，五位数要为奇数，则个位数只能是1，3，5；分为两步：先从1，3，5三个数中选一个作为个位数有C13，再将剩下的4个数字排列得到A44，则满足条件的五位数有C13·A44＝72.选D.]4.(2016·北京，8)袋中装有偶数个球，其中红球、黑球各占一半.甲、乙、丙是三个空盒，每次从袋中任意取出两个球，将其中一个球放入甲盒，如果这个球是红球，就将另一个球放入乙盒，否则就放入丙盒.重复上述过程，直到袋中所有球都被放入盒中，则()A.乙盒中黑球不多于丙盒中黑球B.乙盒中红球与丙盒中黑球一样多C.乙盒中红球不多于丙盒中红球D.乙盒中黑球与丙盒中红球一样多4.B [取两个球往盒子中放有4种情况：①红＋红，则乙盒中红球数加1个；②黑＋黑，则丙盒中黑球数加1个；③红＋黑(红球放入甲盒中)，则乙盒中黑球数加1个；④黑＋红(黑球放入甲盒中)，则丙盒中红球数加1个；因为红球和黑球个数一样，所以①和②的情况一样多.③和④的情况随机，③和④对B选项中的乙盒中的红球与丙盒中的黑球数没有任何影响，①和②出现的次数是一样的，所以对B选项中的乙盒中的红球与丙盒中的黑球数的影响次数一样.综上选B.]5.(2015·四川，6)用数字0,1,2,3,4,5组成没有重复数字的五位数，其中比40 000大的偶数共有()A.144个B.120个C.96个D.72个5.B[由题意,首位数字只能是4,5,若万位是5,则有3×A34＝72个；若万位是4，则有2×A34个＝48个，故40 000大的偶数共有72＋48＝120个.选B.]6.(2014·大纲全国，5)有6名男医生、5名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有()A.60种B.70种C.75种D.150种6.C[从中选出2名男医生的选法有C26＝15种，从中选出1名女医生的选法有C15＝5种，所以不同的选法共有15×5＝75种，故选C.]7.(2014·辽宁，6)6把椅子摆成一排，3人随机就座，任何两人不相邻的坐法种数为()A.144B.120C.72D.247.D[3人中每两人之间恰有一个空座位，有A33×2＝12种坐法，3人中某两人之间有两个空座位，有A33×A22＝12种坐法，所以共有12＋12＝24种坐法.]8.(2014·四川，6)六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有()A.192种B.216种C.240种D.288种8.B[当最左端排甲时，不同的排法共有A55种；当最左端排乙时，甲只能排在中间四个位置之一，则不同的排法共有C14A44种.故不同的排法共有A55＋C14A44＝9×24＝216种.]9.(2014·重庆，9)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序，则同类节目不相邻的排法种数是()A.72B.120C.144D.1689.B[依题意，先仅考虑3个歌舞类节目互不相邻的排法种数为A33A34＝144，其中3个歌舞类节目互不相邻但2个小品类节目相邻的排法种数为A22A22A33＝24，因此满足题意的排法种数为144－24＝120，选B.]10.(2014·安徽，8)从正方体六个面的对角线中任取两条作为一对，其中所成的角为60°的共有()A.24对B.30对C.48对D.60对10.C[法一直接法：如图，在上底面中选B1D1，四个侧面中的面对角线都与它成60°，共8对，同样A1C1对应的也有8对，下底面也有16对，这共有32对；左右侧面与前后侧面中共有16对.所以全部共有48对.法二间接法：正方体的12条面对角线中，任意两条垂直、平行或成角为60°，所以成角为60°的共有C212－12－6＝48对.]11.(2014·福建，10)用a代表红球，b代表蓝球，c代表黑球.由加法原理及乘法原理，从1个红球和1个蓝球中取出若干个球的所有取法可由(1＋a)(1＋b)的展开式1＋a＋b＋ab表示出来，如：“1”表示一个球都不取、“a”表示取出一个红球、而“ab”则表示把红球和蓝球都取出来.依此类推，下列各式中，其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球，且所有的蓝球都取出或都不取出的所有取法的是()A.(1＋a＋a2＋a3＋a4＋a5)(1＋b5)(1＋c)5B.(1＋a5)(1＋b＋b2＋b3＋b4＋b5)(1＋c)5C.(1＋a)5(1＋b＋b2＋b3＋b4＋b5)(1＋c5)D.(1＋a5)(1＋b)5(1＋c＋c2＋c3＋c4＋c5)11.A[分三步：第一步,5个无区别的红球可能取出0个,1个,…,5个,则有(1＋a＋a2＋a3＋a4＋a5)种不同的取法；第二步，5个无区别的蓝球都取出或都不取出，则有(1＋b5)种不同取法；第三步，5个有区别的黑球看作5个不同色，从5个不同色的黑球中任取0个，1个，…，5个，有(1＋c)5种不同的取法，所以所求的取法种数为(1＋a＋a2＋a3＋a4＋a5)(1＋b5)(1＋c)5，故选A.]12.(2014·广东，8)设集合A＝{(x1，x2，x3，x4，x5)|x i∈{－1,0,1}，i＝1,2,3,4,5}，那么集合A中满足条件“1≤|x1|＋|x2|＋|x3|＋|x4|＋|x5|≤3”的元素个数为()A.60B.90C.120D.13012.D[易知|x1|＋|x2|＋|x3|＋|x4|＋|x5|＝1或2或3，下面分三种情况讨论.其一：|x1|＋|x2|＋|x3|＋|x4|＋|x5|＝1，此时，从x1，x2，x3，x4，x5中任取一个让其等于1或－1，其余等于0，于是有C15C12＝10种情况；其二：|x1|＋|x2|＋|x3|＋|x4|＋|x5|＝2，此时，从x1，x2，x3，x4，x5中任取两个让其都等于1或都等于－1或一个等于1、另一个等于－1，其余等于0，于是有2C25＋C25C12＝40种情况；其三：|x1|＋|x2|＋|x3|＋|x4|＋|x5|＝3，此时，从x1，x2，x3，x4，x5中任取三个让其都等于1或都等于－1或两个等于1、另一个等于－1或两个等于－1、另一个等于1，其余等于0，于是有2C35＋C35C13＋C35C23＝80种情况.由于10＋40＋80＝130，故答案为D.]13.(2015·广东，12)某高三毕业班有40人，同学之间两两彼此给对方仅写一条毕业留言，那么全班共写了________条毕业留言(用数字作答).13.1 560 [依题两两彼此给对方写一条毕业留言相当于从40人中任选两人的排列数，所以全班共写了A 240＝40×39＝1 560条毕业留言.]14.(2014·北京，13)把5件不同产品摆成一排，若产品A 与产品B 相邻，且产品A 与产品C 不相邻，则不同的摆法有________种.14.36 [将A 、B 捆绑在一起，有A 22种摆法，再将它们与其他3件产品全排列，有A 44种摆法，共有A 22A 44＝48种摆法，而A 、B 、C 3件在一起，且A 、B 相邻，A 、C 相邻有CAB 、BAC 两种情况，将这3件与剩下2件全排列，有2×A 33＝12种摆法，故A 、B 相邻，A 、C 不相邻的摆法有48－12＝36种.]15.(2014·浙江，14)在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有________种(用数字作答).15.60 [分情况：一种情况将有奖的奖券按2张、1张分给4个人中的2个人，种数为C 23C 11A 24＝36；另一种将3张有奖的奖券分给4个人中的3个人，种数为A 34＝24，则获奖情况总共有36＋24＝60(种).]考点2 二项式定理及其应用1.(2016·四川，2)设i 为虚数单位，则(x ＋i)6的展开式中含x 4的项为( ) A.-15x 4 B.15x 4 C.-20i x 4 D.20i x 41. A [由题可知，含x 4的项为C 26x 4i 2＝－15x 4.选A.]2.(2015·新课标全国Ⅰ，10)(x 2＋x ＋y )5的展开式中，x 5y 2的系数为( ) A.10 B.20 C.30 D.602.C [T k ＋1＝C k 5(x 2＋x )5－k y k ，∴k ＝2.∴C 25(x 2＋x )3y 2的第r ＋1项为C 25C r 3x2(3－r )x r y 2，∴2(3－r )＋r ＝5，解得r ＝1，∴x 5y 2的系数为C 25C 13＝30.]3.(2015·湖南，6)已知⎝⎛⎭⎫x －a x 5的展开式中含32x 的项的系数为30，则a ＝( )A. 3B.－ 3C.6D.－63.D [⎝⎛⎭⎫x －a x 5的展开式通项T r ＋1＝C r 5x 5－r 2(－1)r a r ·x －r 2＝(－1)r a r C r 5x 52－r，令52－r ＝32，则r ＝1，∴T 2＝－a C 15x 32，∴－a C 15＝30，∴a ＝－6，故选D.]4.(2015·陕西，4)二项式(x ＋1)n (n ∈N ＋)的展开式中x 2的系数为15，则n ＝( ) A.4 B.5 C.6 D.74.C [由题意易得：C n －2n ＝15，C n －2n ＝C 2n ＝15，即n （n －1）2＝15，解得n ＝6.]5.(2014·湖北，2)若二项式⎝⎛⎭⎫2x ＋a x 7的展开式中1x 3的系数是84，则实数a ＝( ) A.2 B.54 C.1 D.245.C[T r ＋1＝C r 7·(2x )7－r·⎝⎛⎫a x r＝27－r C r7a r ·1x2r －7.令2r －7＝3，则r ＝5.由22·C 57a 5＝84得a ＝1，故选C.]6.(2014·浙江，5)在(1＋x )6(1＋y )4的展开式中，记x m y n 项的系数f (m ，n )，则f (3,0)＋f (2,1)＋f (1,2)＋f (0,3)＝( )A.45B.60C.120D.2106.C [在(1＋x )6的展开式中，x m 的系数为C m 6，在(1＋y )4的展开式中，y n 的系数为C n4，故f (m ，n )＝C m 6·C n 4.从而f (3，0)＝C 36＝20，f (2，1)＝C 26·C 14＝60,f (1，2)＝C 16·C 24＝36,f (0，3)＝C 34＝4，故选C.]7.(2014·四川，2)在x (1＋x )6的展开式中，含x 3项的系数为( ) A.30 B.20 C.15 D.107.C [只需求(1＋x )6的展开式中含x 2项的系数即可,而含x 2项的系数为C 26＝15，故选C.]8.(2014·湖南，4)⎝⎛⎭⎫12x －2y 5的展开式中x 2y 3的系数是( ) A.－20 B.－5 C.5 D.208.A [展开式的通项为T k ＋1＝C k 5(12x )5－k ·(－2y )k ＝(－1)k ·22k －5C k 5x 5－k·y k ，令5－k ＝2，得k ＝3.则展开式中x 2y 3的系数为(－1)3·22×3－5C 35＝－20，故选A.]9.(2016·全国Ⅰ，14)(2x ＋x )5的展开式中，x 3的系数是______________(用数字填写答案). 9.10 [(2x ＋x )5展开式的通项公式T k ＋1＝C k 5(2x )5－k(x )k＝C k 525－k x 5－k2，k ∈{0,1,2,3,4,5}，令5－k 2＝3解得k ＝4，得T 5＝C 4525－4x 5－42＝10x 3，∴x 3的系数是10.]10.(2016·北京，10)在(1－2x )6的展开式中，x 2的系数为________.10. 60 [展开式的通项T r ＋1＝C r 6·16－r ·(－2x )r ＝C r 6(－2x )r .令r ＝2得T 3＝C 26·4x 2＝60x 2，即x 2的系数为60.]11.(2015·北京，9)在(2＋x )5的展开式中，x 3的系数为________(用数字作答).11.40 [展开式通项为：T r ＋1＝C r 525－r x r ，∴当r ＝3时，系数为C 35·25－3＝40.]12.(2015·天津，12)在⎝⎛⎭⎫x －14x 6的展开式中，x 2的系数为________. 12.1516 [⎝⎛⎭⎫x －14x 6的展开式的通项T r ＋1＝C r 6x 6－r ⎝⎛⎭⎫－14x r ＝C r 6⎝⎛⎭⎫－14r x 6－2r ；当6－2r ＝2时，r ＝2，所以x 2的系数为C 26⎝⎛⎭⎫－142＝1516.]13.(2014·新课标全国Ⅰ，13)(x －y )(x ＋y )8的展开式中x 2y 7的系数为________(用数字填写答案).13.－20 [由二项展开式公式可知，含x 2y 7的项可表示为x ·C 78xy 7－y ·C 68x 2y 6，故(x －y )(x ＋y )8的展开式中x 2y 7的系数为C 78－C 68＝C 18－C 28＝8－28＝－20.]14.(2014·新课标全国Ⅱ，13)(x ＋a )10的展开式中，x 7的系数为15，则a ＝________(用数字作答). 14.12 [T r ＋1＝C r 10x 10－r a r ,令10－r ＝7,得r ＝3,∴C 310a 3＝15，即10×9×83×2×1a 3＝15,∴a 3＝18，∴a ＝12.]15.(2014·安徽，13)设a ≠0，n 是大于1的自然数，⎝⎛⎭⎫1＋xa n 的展开式为a 0＋a 1x ＋a 2x 2＋…＋a n x n .若点A i (i ，a i )(i ＝0,1,2)的位置如图所示，则a ＝________.15.3 [根据题意知a 0＝1，a 1＝3，a 2＝4，结合二项式定理得⎩⎨⎧C 1n ·1a＝3，C 2n·1a 2＝4，即⎩⎪⎨⎪⎧n －1＝83a ，n ＝3a ，解得a ＝3.]16.(2014·山东，14)若⎝⎛⎭⎫ax 2＋bx 6的展开式中x 3项的系数为20，则a 2＋b 2的最小值为________. 16.2[T r ＋1＝C r 6(ax 2)6－r⎝⎛⎭⎫b x r＝C r6a 6－rb r x 12－3r ，令12－3r ＝3，则r ＝3. ∴C 36a 3b 3＝20，即ab ＝1.∴a 2＋b 2≥2ab ＝2，即a 2＋b 2的最小值为2.]17.(2014·大纲全国，13)⎝⎛⎭⎫ x y －yx 8的展开式中x 2y 2的系数为________(用数字作答). 17.70[T r ＋1＝C r 8·⎝⎛⎭⎫x y 8－r ·⎝⎛⎭⎫－y x r＝(－1)r ·C r 8·x 16－3r 2·y 3r －82，令⎩⎨⎧16－3r2＝2，3r －82＝2，得r ＝4.所以展开式中x 2y 2的系数为(－1)4·C 48＝70.]。

北京市2018届高三理科数学一轮复习试题选编24：计数原理一、选择题 1 ．（2017北京理）6.从0,2中选一个数字.从1.3.5中选两个数字,组成无重复数字的三位数.其中奇数的个数为 （ ） A ．24 B ．18 C ．12 D ．6 【答案】【解析】由于题目要求的是奇数,那么对于此三位数可以分成两种情况:奇偶奇;偶奇奇.如果是第一种奇偶奇的情况,可以从个位开始分析(3种选择),之后十位(2种选择),最后百位(2种选择),共12种;如果是第二种情况偶奇奇,分析同理:个位(3种情况),十位(2种情况),百位(不能是0,一种情况),共6种,因此总共12+6=18种情况. 【答案】B2 ．（2018北京丰台二模数学理科试题及答案）41()x x-展开式中的常数项是 （ ）A ．6B ．4C ．-4D ．-6 【答案】A ． 3 ．（北京市朝阳区2018届高三上学期期末考试数学理试题 ）某中学从4名男生和3名女生中推荐4人参加社会公益活动，若选出的4人中既有男生又有女生，则不同的选法共有 （ ） A ．140种 B ．120种 C ．35种 D ．34种【答案】D解：若选1男3女有13434C C =种；若选2男2女有224318C C =种；若选3男1女有314312C C =种；所以共有4181234++=种不同的选法。

选 D ．4 ．（2018届北京市延庆县一模数学理）现有12件商品摆放在货架上，摆成上层4件下层8件，现要从下层8件中取2件调整到上层，若其他商品的相对顺序不变，则不同调整方法的种数是 （ ） A ．420 B ．560 C ．840 D ．20160 【答案】C5 ．（2018届北京西城区一模理科）从甲、乙等5名志愿者中选出4名，分别从事A ，B ，C ，D 四项不同的工作，每人承担一项．若甲、乙二人均不能从事A 工作，则不同的工作分配方案共有 （ ）A ．60种B ．72种C ．84种D ．96种【答案】B 6 ．（2010年高考（北京理））8名学生和2位老师站成一排合影,2位老师不相邻的排法种数为 （ ）A ．8289A AB ．8289A CC ．8287A AD ．8287A C【答案】A ;解:8名学生先排成一排,有88A 种排法,在他们的9个空中插入两名教师,有29A 种方法,所以排法总数为8289A A ,选（ ）A ．7 ．（2009高考(北京理)）若5(1)(,a a b =+为有理数),则a b += （ ）A ．45B ．55C ．70D ．80 【答案】C【解析】本题主要考查二项式定理及其展开式. 属于基础知识、基本运算的考查.∵(5123450123455555551CCC CC C=+++++1202041=++++由已知,得41a +=+412970a b +=+=.故选C ．8 ．（2009高考(北京理)）用0到9这10个数字,可以组成没有重复数字的三位偶数的个数为 （ ） A ．324 B ．328 C ．360 D ．648 【答案】B【解析】本题主要考查排列组合知识以及分类计数原理和分步计数原理知识. 属于基础知识、基本运算的考查.首先应考虑“0”是特殊元素,当0排在末位时,有299872A =⨯=(个), 当0不排在末位时,有111488488256A A A ⋅⋅=⨯⨯=(个),于是由分类计数原理,得符合题意的偶数共有72256328+=(个).故选 B ． 9 ．（北京市昌平区2018届高三上学期期末考试数学理试题 ）在高三（1）班进行的演讲比赛中，共有5位选手参加，其中3位女生，2位男生.如果2位男生不能连续出场，且女生甲不能排在第一个，那么出场顺序的排法种数为 （ ） A ．24 B ．36 C ．48 D ．60【答案】D解：先排3个女生，三个女生之间有4个空，从四个空中选两个排男生，共有2343=72A A 种，若女生甲排在第一个，则三个女生之间有3个空，从3个空中选两个排男生，有2232=12A A ，所以满足条件的出错顺序有7212=60-种排法，选 D ． 10．（2018北京海淀二模数学理科试题及答案）用数字1,2,3,4,5组成没有重复数字的五位数,且5不排在百位,2,4都不排在个位和万位,则这样的五位数个数为 （ ）A ．32B ．36C ．42D ．48【答案】 （ ）A ．11．（北京市海淀区2018届高三上学期期末考试数学理试题 ）用数字0,1,2,3组成数字可以重复的四位数, 其中有且只有一个数字出现两次的四位数的个数为 （ ）A ．144B ．120C ．108D ．72【答案】C解：若四位数中不含0，则有12234236C C A =种；若四位数中含有一个0，则有1121333254C C C A =；种若四位数中含有两个0，则有223318C A =种，所以共有365418108++=种，选 C ．12．（北京市石景山区2018届高三一模数学理试题）在(2x 2-1x)5的二项展开式中,x 的系数为（ ）A ．-10B ．10C ．-40D ．40【答案】C 13．（2018北京丰台二模数学理科试题及答案）用5,6,7,8,9组成没有重复数字的五位数,其中两个偶数数字之间恰有一个奇数数字的五位数的个数是 （ ） A ．18 B ．36 C ．54 D ．72 【答案】 B ． 14．（北京市石景山区2018届高三上学期期末考试数学理试题 ）若从1,2,3,…,9这9个整数中同时取4个不同的数，其和为奇数，则不同的取法共有 （ ） A ．60种 B ．63种 C ．65种 D ．66种【答案】A解：若四个数之和为奇数，则有1奇数3个偶数或者3个奇数1个偶数。