第9章 传热过程和换热器的计算

传热过程及换热器1.燃烧炉的平壁是一层耐火砖和一层普通砖砌成，内层耐火砖厚度为230mm ，外层普通砖厚度为240mm ，当达到定态传热时，测得炉内壁温度是700℃，外表面温度是100℃，为了减少热量损失，在普通砖外面加砌一层厚度为40mm 的保温材料，当定态后测得内壁面温度为720℃，保温材料外表面温度为70℃。

求加保温材料前后每平方壁面热损失是多少？耐火砖、普通砖、保温材料的热导率分别为1.163W·m -1·℃-1，0.5815W·m -1·℃-1，0.07W·m -1·℃-1。

解：根据多层平壁热传导公式：i iit Q A δλΣΔ=Σ 加保温材料前：Σt i =t 1-t n+1=700-100=600℃0.230.241.1630.58150.6105i i δλΣ=+= 26000.6105982.8W/m Q A == 加保温材料后：Σt i =t 1-t n+1=720-70=650℃0.230.240.041.1630. 1.18581500720.i i δλΣ=++= 2545W/m 1.186250Q A == 2.如习题1加保温材料后测得内壁面温度为720℃，保温材料外表面温度为70℃。

计算耐火砖与普通砖、普通砖与保温材料间的交界面温度。

解：加保温材料后，传热速率为：2545W/m 1.186250Q A == 根据平壁热传导公式：1211545t t Q Aδλ−== t 1=720；λ1=1.163W·m -1·℃-1，δ1=0.24m 代入上式解得：t 2=1110.23720545 1.1636211.Q t A δλ−⋅=−×=℃ 同理得 t 3=3430.0470545031.74.08Q t A δλ+⋅=+×=℃ 3.平壁炉的炉壁内层为120mm 厚的耐火材料和外壁厚度为230mm 建筑材料砌成，两种材料的导热系数为未知，测得炉内壁面温度为800℃，外侧壁面温度113℃，后来在普通建筑材料外面又包一层厚度为50mm 的石棉以减少热损失，包扎后测得炉内壁面温度为800℃，耐火材料与建筑材料交界面温度为686℃，建筑材料与石棉交界面温度为405℃，石棉外侧温度为77℃，问包扎石棉后热损失比原来减少的百分数？解：包石棉材料前得传热速率1128001130.120.23tQ δλλλΣΔ−==Σ+ 包石棉材料后得传热速率2128004050.120.23tQ δλλλΣΔ−==Σ+ 包扎石棉后热损失比原来减少的百分数=21800405110.425=42.45%800113Q Q −−==−=− 4.φ50mm×5mm 的不锈钢管(λ1=16 W·m -1·K -1)外包扎厚度为30mm 的石棉(λ2=0.22 W·m -1·K -1),若管内壁温度为600℃，石棉外壁面温度100℃，求每米管线的热损失。

换热器的传热及阻力计算换热器是一种用于传递热量的设备，广泛应用于各个领域，如工业生产、能源系统和空调系统等。

在设计换热器时，需要对其进行传热及阻力计算，以确保其正常工作和高效性能。

本文将详细介绍换热器的传热计算方法和阻力计算方法。

换热器的传热计算方法可以通过换热系数和传热面积两个方面来进行。

换热系数是一个反映传热效率的参数，可以通过实验测定或理论计算得到。

传热面积是指换热器内热量传递的表面积，可以通过换热器的几何形状和尺寸进行计算。

换热系数的计算方法主要有理论计算和实验测定两种。

理论计算方法是根据换热过程涉及的热力学和流体力学原理，利用换热器材料的导热性能、流体的物性参数和流体速度等来计算换热系数。

而实验测定方法则是通过实验室或现场实测来确定换热系数。

常见的实验测定方法有柱式法、风洞法、加热线法和表面平均温度法等。

传热面积的计算方法则根据具体的换热器结构形式来进行。

换热面积的计算需要考虑换热器的传热面的几何形状、尺寸和布置等因素。

根据实际情况和设计要求，可以选择适当的换热器结构，如管壳式、板式、管翅片式、环型或螺旋板式等，并根据具体结构进行面积计算。

阻力计算是指换热器在工作过程中对流体流动产生的阻力进行估算。

对流体流动的阻力计算需要考虑流体的运动状态、流量和流速等因素。

阻力计算可以通过实验测定或理论计算来进行。

实验测定方法包括风洞法、压差容器法和管道试验法等，其中风洞法是常用的方法之一、理论计算方法则根据流体流动的基本原理和方程来进行，如伯努利方程、连续性方程和动量方程等。

在进行换热器的阻力计算时，需要考虑流体的性质、流动状态和流道的几何形状等因素。

一般来说，流体的阻力与其粘度、密度、流速和流体的流动形式等有关。

流体的流动形式可以分为层流和紊流两种，其阻力特性也有所不同。

通常情况下，层流和紊流的阻力可以通过一系列经验公式或实验数据进行计算和估算。

除了传热计算和阻力计算，还需要对换热器进行性能评估和优化设计。

第九章 传热过程分析和换热器计算在这一章里讨论几种典型的传热过程，如通过平壁、圆筒壁和肋壁的传热过程通过分析得出它们的计算公式。

由于换热器是工程上常用的热交换设备，其中的热交换过程都是一些典型的传热过程。

因此，在这里我们对一些简单的换热器进行热平衡分析，介绍它们的热计算方法，以此作为应用传热学知识的一个较为完整的实例。

9－1传热过程分析在实际的工业过程和日常生活中存在着的大量的热量传递过程常常不是以单一的热量传递方式出现，而多是以复合的或综合的方式出现。

在这些同时存在多种热量传递方式的热传递过程中，我们常常把传热过程和复合换热过程作为研究和讨论的重点。

对于前者，传热过程是定义为热流体通过固体壁面把热量传给冷流体的综合热量传递过程，在第一章中我们对通过大平壁的传热过程进行了简单的分析，并给出了计算传热量的公式 t kF Q ∆=， 9－1式中，Q 为冷热流体之间的传热热流量，W ；F 为传热面积，m 2；t ∆为热流体与冷流体间的某个平均温差，oC ；k 为传热系数，W/(⋅2m o C)。

在数值上，传热系数等于冷、热流体间温差t ∆=1 o C 、传热面积A =1 m2时的热流量值，是一个表征传热过程强烈程度的物理量。

在这一章中我们除对通过平壁的传热过程进行较为详细的讨论之外，还要讨论通过圆筒壁的传热过程，通过肋壁的传热过程，以及在此基础上对一些简单的包含传热过程的换热器进行相应的热分析和热计算。

对于后者，复合换热是定义为在同一个换热表面上同时存在着两种以上的热量传递方式，如气体和固体壁面之间的热传递过程，就同时存在着固体壁面和气体之间的对流换热以及因气体为透明介质而发生的固体壁面和包围该固体壁面的物体之间的辐射换热，如果气体为有辐射性能的气体，那么还存在固体壁面和气体之间的辐射换热。

这样，固体壁面和它所处的环境之间就存在着一个复合换热过程。

下面我们来讨论一个典型的复合换热过程，即一个热表面在环境中的冷却过程，如图9－1所示。

第九章 传热过程分析和换热器计算在这一章里讨论几种典型的传热过程，如通过平壁、圆筒壁和肋壁的传热过程通过分析得出它们的计算公式。

由于换热器是工程上常用的热交换设备，其中的热交换过程都是一些典型的传热过程。

因此，在这里我们对一些简单的换热器进行热平衡分析，介绍它们的热计算方法，以此作为应用传热学知识的一个较为完整的实例。

9－1传热过程分析在实际的工业过程和日常生活中存在着的大量的热量传递过程常常不是以单一的热量传递方式出现，而多是以复合的或综合的方式出现。

在这些同时存在多种热量传递方式的热传递过程中，我们常常把传热过程和复合换热过程作为研究和讨论的重点。

对于前者，传热过程是定义为热流体通过固体壁面把热量传给冷流体的综合热量传递过程，在第一章中我们对通过大平壁的传热过程进行了简单的分析，并给出了计算传热量的公式 t kF Q ∆=， 9－1式中，Q 为冷热流体之间的传热热流量，W ；F 为传热面积，m 2；t ∆为热流体与冷流体间的某个平均温差，o C ；k 为传热系数，W/(⋅2m o C)。

在数值上，传热系数等于冷、热流体间温差t ∆=1 o C 、传热面积A =1 m 2时的热流量值，是一个表征传热过程强烈程度的物理量。

在这一章中我们除对通过平壁的传热过程进行较为详细的讨论之外，还要讨论通过圆筒壁的传热过程，通过肋壁的传热过程，以及在此基础上对一些简单的包含传热过程的换热器进行相应的热分析和热计算。

对于后者，复合换热是定义为在同一个换热表面上同时存在着两种以上的热量传递方式，如气体和固体壁面之间的热传递过程，就同时存在着固体壁面和气体之间的对流换热以及因气体为透明介质而发生的固体壁面和包围该固体壁面的物体之间的辐射换热，如果气体为有辐射性能的气体，那么还存在固体壁面和气体之间的辐射换热。

这样，固体壁面和它所处的环境之间就存在着一个复合换热过程。

下面我们来讨论一个典型的复合换热过程，即一个热表面在环境中的冷却过程，如图9－1所示。

第五节 传热过程的计算化工生产中广泛采用间壁换热方法进行热量的传递。

间壁换热过程由固体壁的导热和壁两侧流体的对流传热组合而成，导热和对流传热的规律前面已讨论过，本节在此基础上进一步讨论传热的计算问题。

化工原理中所涉及的传热过程计算主要有两类：一类是设计计算，即根据生产要求的热负荷，确定换热器的传热面积；另一类是校核计算，即计算给定换热器的传热量、流体的流量或温度等。

两者都是以换热器的热量衡算和传热速率方程为计算基础。

4-5-1 热量衡算流体在间壁两侧进行稳定传热时，在不考虑热损失的情况下，单位时间热流体放出的热量应等于冷流体吸收的热量，即：Q=Q c =Q h （4-59） 式中 Q ——换热器的热负荷，即单位时间热流体向冷流体传递的热量，W ； Q h ——单位时间热流体放出热量，W ； Q c ——单位时间冷流体吸收热量，W 。

若换热器间壁两侧流体无相变化，且流体的比热容不随温度而变或可取平均温度下的比热容时，式（4-59）可表示为()()1221t t c W T T c W Q pc c ph h -=-= （4-60） 式中 c p ——流体的平均比热容，kJ/（kg ·℃）； t ——冷流体的温度，℃； T ——热流体的温度，℃； W ——流体的质量流量，kg/h 。

若换热器中的热流体有相变化，例如饱和蒸气冷凝，则()12t t c W r W Q pc c h -== （4-61） 式中 W h ——饱和蒸气（即热流体）的冷凝速率，kg/h ； r ——饱和蒸气的冷凝潜热，kJ/kg 。

式（4-61）的应用条件是冷凝液在饱和温度下离开换热器。

若冷凝液的温度低于饱和温度时，则式（4-61）变为()[]()122t t c W T T c r W Q pc c s ph h -=-+= （4-62） 式中 c ph ——冷凝液的比热容，kJ/（kg ·℃）； T s ——冷凝液的饱和温度，℃。

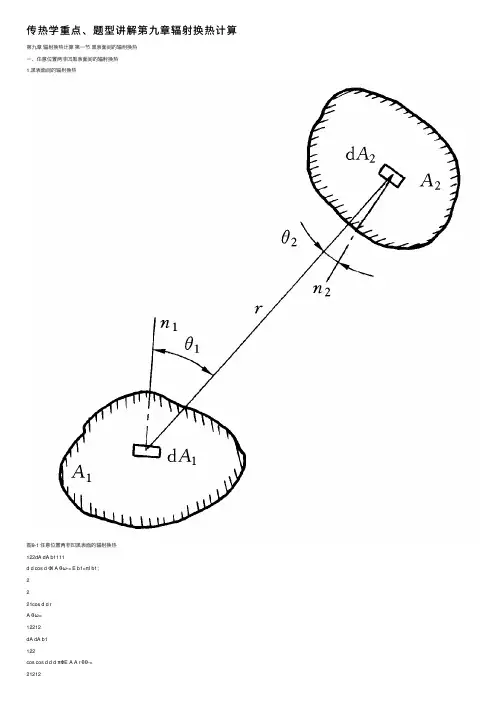
传热学重点、题型讲解第九章辐射换热计算第九章辐射换热计算第⼀节⿊表⾯间的辐射换热⼀、任意位置两⾮凹⿊表⾯间的辐射换热1.⿊表⾯间的辐射换热图9-1 任意位置两⾮凹⿊表⾯的辐射换热122dA dA b1111d d cos d ΦI A θω-= E b1=πI b1；2221cos d d rA θω=12212dA dA b1122cos cos d d d πΦE A A r θθ-=21212dA dA b2122cos cos d d d πΦE A A r θθ-=12122122212dA ,dA dA dA dA dA b1b2122cos cos d d d ()d d πΦΦΦE E A A rθθ--=-=- 1212122121,2dA ,dA b1b2122cos cos d ()d d πA A A A ΦΦE E A A r θθ==- （9-1）2.⾓系数12121122b1122dA dA 12dA ,dA 22dA b11cos cos d d d cos cos πd d d πE A A Φr X A ΦE A r θθθθ-= ==12122121122dA dA 2dA A 12dA ,A 22dA dA d d cos cos d d d πA A ΦΦX A ΦΦr θθ--===12 1212 1112 2dA dA A A12 1,212 2A A1 dcos cos 1d dπA AA AΦΦX A A ΦΦA r θθ--（9-2a）212212AAA1,2ddπcoscos121212AArAΦΦXAA==-θθ（9-2b）21,212,1AXAX=（9-3）3.辐射空间热阻图9-2 辐射空间热阻21,2b2b112,1b2b12,1)(AXEEAXEEΦ-=-=（9-4）b1b21,21,211E EΦX A-=Φ1,2=（E b1－E b2）A = σb（T14- T24）A ⼆、封闭空腔诸⿊表⾯间的辐射换热图9-3 多个⿊表⾯组成的空腔图9-4 三个⿊表⾯组成空腔的辐射⽹络图9-5 例9-1附图：,1,2,,1ni i i i n i j j ΦΦΦΦΦ==++=∑将上式除以i Φ，按⾓系数定义，可得,1,2,n ,11ni i i i j j X X X X ==++=∑（9-5）∑∑∑∑====-=-==nj nj i j i nj i j i i j i nj j i i A X E A X E A X E E ΦΦ11,bj 1,bi ,bj bi 1,)(∑=-=nj j i j i i A X E A E Φ1,bj bi （9-6）【例9-1】∑=-=311,b 1b11j j j j A X E A E Φ（a ）∑=-=312,b 2b22j j j j A X E A E Φ（b ）0313,b 3b33=-=∑=j j j j A X E A E Φ（c ）02,21,22,11,1====X X X X13,23,1==X X31,313,1A X A X =32,323,2A X A X =213,11,33,223/210.252A r X X X A r ππ==?==13,32,31,3=++X X X 5.03,3=X033,3b323,2b213,1b13b3=---A X E A X E A X E A E4b b T E σ=2424143T T T +=T 3=415.6K 或者142.6℃1b11b11,11b22,12b33,1344b11b31,3111344311b 244()()()100100473415.61 5.67()()1801.0W 2100100b ΦE A E X A E X A E X A E A E X A A T T T T AC σπ=---=-=-??=-=???-=????【讨论】π411212121=+=+=∑A A A A A AR 4444b1b2121,2()π5.67 4.73 3.13)1801.0W 4/π4b E E T T ΦRσ--===??-=∑（第⼆节灰表⾯间的辐射换热⼀、有效辐射图9-6 有效辐射⽰意图图9-7 辐射表⾯热阻1.有效辐射J 1=ε1E b1＋ρ1G 1=ε1E b1＋（1－α1）G 1 W/m 2（a ）2.辐射表⾯热阻11b111111G E G J A Φαε-=-= W/m 2 （b ） 1111b11b111111)(1A J E J E A Φεεεε--=--=W （9-7）⼆、组成封闭腔的两灰表⾯间的辐射换热图9-8 两个灰表⾯组成封闭腔的辐射换热⽹络图9-9 空腔与内包壁⾯间的辐射换热22212,1111b2b12,1111A A X A E E Φεεεε-++--=W (9-8a ))11(1)11()(2212,112b 1b 12,1-++--=εεA A X E E A Φ 1,2112()W s b b X A E E ε=- （9-8b ）)11()11(1121,212,1s -+-+=εεεX X1.⽆限⼤平⾏灰平壁的辐射换热A 1=A 2=A ，且X 1,2=X 2,1=1，)(111)(4241b s 212b b12,1T T A E E A Φ-=-+-=σεεε W （9-9）1121s -+=εεε2.其中⼀个表⾯为平⾯或凸表⾯的辐射换热)11(1)(22112b 1b 12,1-+-=εεA A E E A Φ W (9-10)A 2 >>A 1，且ε2的数值较⼤Φ1,2=ε1 A 1（E b1-E b2）W （9-11）三、封闭空腔中诸灰表⾯间的辐射换热1.⽹络法求解图9-10三个灰表⾯组成封闭腔辐射换热⽹络图9-11 例9-4附图图9-12 例题9-5附图节点1013,11312,1121111b1=-+-+-A X J J A X J J A J E εε（a ）321,2212222b2=-+-+--A X J J A X J J A J E εε（b ）节点3 011132,33231,3313333b3=-+-+--A X J J A X J J A J E εε（c ）【例9-4】X 1,2= X 2,1=0.38X 1,3=X 2,3=1-X 1,2=1-0.38=0.62计算⽹络中的各热阻值：A 1=A 2=π?0.32=0.283m 21.14283.02.02.011111=?-＝－A εε m -23.5283.04.04.011222=?=-－A εε m -23.9283.038.01112,1=?=A X m -27.5283.062.011123,213,1=?==A X A X m -2流⼊每个节点的电流总和等于零07.53.91.141b3121b1=-+-+-J E J J J E 07.53.93.52b3212b2=-+-+-J E J J J E 202447731067.5484b1=??==-T E b σW/m 2 35445001067.5484b2=??==-T E b σW/m24593001067.5484b3=??==-T E b σW/m 2J 1=5129W/m 2J 2=2760W/m 2b1111112024451291072W 114.1E J ΦA εε--===- b22222235442760148W 1 5.3E J ΦA εε--===-312()(1072148)1220W ΦΦΦ=-+=-+=-【例9-5】1.1411111=-=A R εεm -23.512222=-=A R εεm -23.9112,12,1==A X R m -27.5113,13,23,1===A X R R m -2E b1=20244W/m 2E b2=3544W/m 2∑++++=23,23,12,11111R R R R R R =14.1+5.243.57.57.513.911=+++m -2b1b21,2202443544682W 24.5E E ΦR --===∑J 1=E b1－Φ1,2?R 1=20244－682?14.1=10627.8W/m 2J 2=E b2＋Φ1,2?R 2=3544＋682?5.3=7185.6 W/m 2J 3=（J 1+J 2）/2=8893.2 W/m 2J 3=G 3=E b3=σb T 341/41/45.6710b E T σ-=== ?2. 值解法图9-13 例9-6（a ）（b ）附图及其辐射换热⽹络∑==ni i j i i j j A X J G A 1,j j εα=∑=-+=ni i j i i j j j j j j A X J A E A J 1,b )1(εε（9-12）∑∑===ni i j i j ni i ji i X J A A XJ 1,1,b ,1(1)nj j j j i j i i J E J X εε==+-∑（9-13）4b 1,11j j j j jni i j i T J X J σεεε-=--∑= （9-14）4111,121,231,31,b 1114212,122,232,32,b 2221,12,231()()111()()11n n n n n n n J X J X J X J X T J X J X J X J X T J X J X J X εσεεεσεε-++++=--+-+++=--?++4,3,b 1()()11n n n n n n n J X T εσεε?++-=?--? （9-15）ii i i i i A J E Φεε--=1b i =1，2，…n （9-16）【例9-6】1,11,21,31,400.150.540.31X X X X ====、、、；2,12,22,32,40.2500.500.25X X X X ====、、、；3,13,23,33,40.270.140.320.27X X X X ====、、、；4,14,24,34,40.310.150.540X X X X ====、、、；4432198.267.5931.054.015.010??=---J J J J 4432183.267.5425.05.0525.0??=--+-J J J J4432186.267.5427.068.414.027.0??=-+--J J J J 4432184.267.55.15.254.015.031.0??=+---J J J JJ 1=440.45 W/m 2； J 2=370.28W/m 2； J 3=382.69W/m 2 ; J 4=380.80W/m 2。

传热过程和换热器热计算基础前言:在工业生产和日常生活中，传热是一个非常重要的过程。

无论是热运输、能源利用、工业生产还是家庭暖气系统，我们都需要了解传热过程和换热器的热计算基础。

在本文中，我们将详细介绍传热过程的基本概念和传热计算的方法。

一、传热过程的基本概念1、传热的基本概念传热是指能量由高温区域传递到低温区域的过程。

传热过程可以通过三种方式进行传递，分别是传导、对流和辐射。

传导是指热量通过物质的直接接触传递，对流是指热量通过流体（液体或气体）的运动传递，辐射是指热量通过电磁辐射传递。

在实际应用中，这三种传热方式常常同时存在。

例如，热水锅炉中的传热过程包括水的对流传热、锅炉壁的传导传热和辐射传热。

2、传热的基本定律传热过程基于以下两个基本定律，它们是传热计算的基础。

(1)热传导定律热传导定律描述了热量沿着温度梯度的方向从一个物体传递到另一个物体的过程。

热传导定律可以用以下公式表示:q = -kA(dT/dx)其中，q是单位时间内通过单位面积的热流量，k是材料的热传导系数，A是传热的横截面积，dT/dx是温度梯度。

(2)牛顿冷却定律牛顿冷却定律描述了通过对流传热的过程。

它指出，对流换热速率正比于温差和表面积，反比于流体和固体的热阻。

牛顿冷却定律可以用以下公式表示:q=hA(Ts−T∞)其中，q是单位时间内通过单位面积的热流量，h是对流传热系数，A 是传热表面积，Ts是固体表面温度，T∞是流体的温度。

二、换热器的计算基础换热器是用于传递热量的设备，广泛应用于各个行业中。

换热器的设计需要进行热计算，主要包括换热面积的计算和换热系数的计算。

1、换热面积的计算换热面积的计算取决于需要传递的热量流率和温度差。

换热面积可以使用以下公式计算:A=Q/(UΔT)其中，A是换热面积，Q是需要传递的热量流率，U是换热系数，ΔT 是温度差。

2、换热系数的计算换热系数是衡量换热器性能的重要指标之一、换热系数可以通过经验公式、理论公式或实验方法进行计算。

换热器的传热计算换热器的传热计算包括两类：一类是设计型计算，即根据工艺提出的条件，确定换热面积；另一类是校核型计算，即对换热面积的换热器，核算其传热量、流体的流量或温度。

这两种计算均以热量衡算和总传热速率方程为根底。

换热器热负荷Q 值一般由工艺包提供，也可以由所需工艺要求求得。

Q=W c p Δt ，假设流体有相变，Q=c p r 。

热负荷确定后，可由总传热速率方程〔Q=K S Δt 〕求得换热面积，最后根据"化工设备标准系列"确定换热器的选型。

其中总传热系数K=0011h Rs kd bd d d Rs d h d o m i i i i ++++ 〔1〕在实际计算中，总传热系数通常采用推荐值，这些推荐值是从实践中积累或通过实验测定获得的，可以从有关手册中查得。

在选用这些推荐值时，应注意以下几点：1. 设计中管程和壳程的流体应与所选的管程和壳程的流体相一致。

2. 设计中流体的性质〔粘度等〕和状态〔流速等〕应与所选的流体性质和状态相一致。

3. 设计中换热器的类型应与所选的换热器的类型相一致。

4. 总传热系数的推荐值一般围很大，设计时可根据实际情况选取中间的*一数值。

假设需降低设备费可选取较大的K 值；假设需降低操作费用可取较小的K 值。

5. 为保证较好的换热效果，设计中一般流体采用逆流换热，假设采用错流或折流换热时，可通过安德伍德〔Underwood〕和鲍曼〔Bowman〕图算法对Δt进展修正。

虽然这些推荐值给设计带来了很大便利，但是*些情况下，所选K值与实际值出入很大，为防止盲目烦琐的试差计算，可根据式〔1〕对K值估算。

式〔1〕可分为三局部，对流传热热阻、污垢热阻和管壁导热热阻，其中污垢热阻和管壁导热热阻可查相关手册求得。

由此，K值估算最关键的局部就是对流传热系数h的估算。

影响对流传热系数的因素主要有：1.流体的种类和相变化的情况液体、气体和蒸气的对流传热系数都不一样。

牛顿型和非牛顿型流体的也有区别，这里只讨论牛顿型对流传热系数。

换热器的传热计算解析换热器是一种常用的传热设备，用于在两个流体之间转移热量。

它采用传导、对流和辐射传热方式，通过对热传导方程和对流换热方程的求解，可以得到换热器的传热计算解析。

第一步，确定传热区域和传热方式。

换热器的传热区域通常包括管内和管外两个区域，传热方式根据具体的条件可以分为对流传热、辐射传热和传导传热。

第二步，建立传热方程。

对于传热区域内的热传导，可以根据热传导方程进行计算。

对于对流传热，可以使用牛顿冷却定律或其他适用的换热关系进行计算。

对于辐射传热，可以使用斯蒂芬-玻尔兹曼定律进行计算。

第三步，边界条件的确定。

边界条件包括温度边界条件和流体流动边界条件。

温度边界条件可以根据实际情况进行确定，流体流动边界条件可以根据流体流动的特性进行确定。

第四步，求解传热方程。

对于热传导方程，可以使用数值求解方法（如有限差分法、有限元法等）进行计算。

对于对流传热和辐射传热，可以使用经验公式进行估算或者使用数值方法进行求解。

第五步，计算换热系数。

换热器的传热系数是一个重要的参数，它反映了换热器的传热性能。

传热系数可以通过实验测量或者基于经验公式进行估算。

第六步，进行传热计算解析。

根据所得到的传热方程和边界条件，可以进行传热计算解析。

根据实际需求，可以计算换热器的传热速率、传热效率、温度分布等参数，从而评估和优化换热器的设计。

在进行换热器的传热计算解析时，还需要考虑换热器的结构、材料的热物性、流体流动的特性等因素，以及适用的传热理论和模型。

此外，还需要进行传热计算解析的验证和优化，以确保计算结果的准确性和可靠性。

总之，换热器的传热计算解析是一个复杂的过程，需要根据具体情况确定传热方式、建立传热方程、确定边界条件、求解传热方程、计算传热系数等，从而得到相应的传热计算解析结果。

这些结果可以用于优化换热器的设计和评估换热器的传热性能。

第九章传热过程分析与换热器计算思考题1、对于q m1c1≥q m2c2，q m1c1<q m2c2，和q m1c1=q m2c2三种情况，画出顺流与逆流时，冷、热流体温度沿流动方向的变化曲线，注意曲线的凹向和q m c的相对大小。

解：逆流时：q m1c1≥q m2c2q m1c1<q m2c2q m1c1=q m2c2顺流时：q m1c1≥q m2c2q m1c1<q m2c2q m1c1=q m2c22、对壳管式换热器来说，两种流体在下列情况下，何种走管内，何种走管外？(1)清洁与不清洁的；(2)腐蚀性大与小的；(3)温度高与低的；(4)压力大与小的；(5)流量大与小的；(6)粘度大与小的。

答：(1)不清洁流体应在管内，因为壳侧清洗比较困难，而管内可定期折开端盖清洗；(2)腐蚀性大的流体走管内，因为更换管束的代价比更换壳体要低，且如将腐蚀性强的流体置于壳侧，被腐蚀的不仅是壳体，还有管子；(3)温度低的流体置于壳侧，这样可以减小换热器散热损失；(4)压力大的流体置于管内，因为管侧耐压高，且低压流体置于壳侧时有利于减小阻力损；(5)流量大的流体放在管外，横向冲刷管束可使表面传热系数增加；(6)粘度大的流体放在管外，可使管外侧表面传热系数增加。

3、为强化一台冷油器的传热，有人用提高冷却水流速的办法，但发现效果并不显著c试分析原因。

答：冷油器中由于油的粘度较大，对流换热表面传热系数较小，占整个传热过程中热阻的主要部分，而冷却水的对流换热热阻较小，不占主导地位，因而用提高水速的方法，只能减小不占主导地位的水侧热阻，故效果不显著。

4、有一台钢管换热器，热水在管内流动，空气在管束间作多次折流横向冲刷管束以冷却管内热水。

有人提出，为提高冷却效果，采用管外加装肋片并将钢管换成铜管。

请你评价这一方案的合理性。

答：该换热器管内为水的对流换热，管外为空气的对流换热，主要热阻在管外空气侧，因而在管外加装肋片可强化传热。