吉林省榆树市2017-2018学年高一第一学期期中数学试卷

吉林省榆树一中2018-2019学年高一物理上学期期中试题一、选择题：(本大题共12小题，每小题5分，共60分．在每小题的4个选项中，只有一项是符合题目要求的)1．设全集U=R ，集合 {}5,3,1=A ，{}5,4,3,2=B ， 则图中阴影部分表示的集合为 （ ）A ．{}5,3B ．{}3,1 C ．{}5,1 D ． {}4,22．下列四个图形中，不能．．表示函数)(x f y =图像的是 ( )．A B C D3．已知函数 f (x )＝3x -1，1)(+=x x g ，则[])(x g f 的解析式为 ( )．A ．13-xB ．x 3C ．13+xD ．23+x4．函数)12(21log 1)(+=x x f 定义域为 ( )A. ⎪⎭⎫ ⎝⎛-0,21 B. ⎪⎭⎫ ⎝⎛-2,21 C. ⎪⎭⎫ ⎝⎛+∞-,21 D. ()+∞⎪⎭⎫⎝⎛-,00,21 5．下列四组函数中，表示同一函数的是 ( )．A ．f (x )＝1＋x ·1－x ，g (x )＝1－2xB ．f (x )＝|x |，g (x )＝2xC ．f (x )＝1－1－2x x ，g (x )＝x ＋1 D ．f (x )＝lg x 2，g (x )＝2lg x6. 设函数⎩⎨⎧<≥-=1,21,3)(x x x x f x , 若1)(=a f , 则=a ( )A.1或2B.0或1C.0或4D.1或47. 下列函数f (x )中，满足“对任意x 1，x 2∈(0，＋∞)，当x 1＜x 2时，都有f (x 1)＞f (x 2)”的是 ( ). A ．f (x )＝x1 B ．f (x )＝x2C ．f (x )＝e xD ．f (x )＝ln x8．已知定义在R 上的函数f (x )的图象是连续不断的，且有如下对应值表：那么函数f (x )一定存在零点的区间是 （ ） A. (－∞，1) B. (1，2) C. (2，3) D. (3，+∞)9．已知 函数⎪⎩⎪⎨⎧≤+>-+=2),3(2,21)(x x f x x x x f ， 则的值等于 ( )A. B . C . D. 无意义10. 若 2-=πa， 2e b =，⎪⎭⎫⎝⎛=212log c ，则c b a ,,的大小关系是( )A. c b a >> B c a b >> C a b c >> D. b c a >>11．已知 函数m x x f -=)(是定义在区间[]m m---1,3上的奇函数,则 ( )A .B .C. D .与大小不确定12. 已知：偶函数f (x )定义域为 (-∞，0) ∪ (0，+∞)且∈21,x x (-∞，0)上有.)(21x x ≠，若f (－1)＝0，则不等式f (x )＜0的解集是 ( ). A ．(－∞，－1)∪(0，1) B ．(－∞，－1)∪(1，＋∞) C ．(－1，0)∪(0，1)D ．(－1，0)∪(1，＋∞)二、填空题：（本大题共4小题，每小题5分，共20分）x 1 2 3 f (x ) 6.1 2.9 －3.513．已知：函数xx x f 2log 2)(+=，则=)1(f14. 计算：=-+521log lg lg 323．15．已知：已知函数)10(,1)(3≠>+=-a a ax f x 且过定点),(n m则函数n x m x x f ++-=)1()(2的单调递增区间是 ． (用区间表示)16．已知奇函数()x f 的定义域是[]2,2-， 对于任意∈21,x x []2,0有[]0)()()(2121<--x f x f x x .)(21x x ≠，若()0)1(>-+m m f ,则m 的取值范围是 ．三、解答题：（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤）17（本题10分）设全集为R ，{}63<<=x x A ，{}9121<-<=x x B求 ( Ⅰ ) B A （本小题5分）( Ⅱ ) ()R C A B （本小题5分）18. （本题10分） 已知函数1)(-=x a x f 的图像经过点⎪⎭⎫ ⎝⎛21,2，其中10≠>a a 且( Ⅰ )求a 的值 （本小题5分）( Ⅱ ) 若,1)(0≥x f 求0x 的取值范围 （本小题5分）19．（本题10分）已知函数)2lg()(x x f +=，)lg()(x m x g -=且0)1(=g( Ⅰ )求函数)(x g 的解析式； （本小题5分）( Ⅱ )判断函数)()()(x g x f x F +=的奇偶性，并说明理由．（本小题5分）20.（本题15分）已知全集R U =,集合A 是函数)4lg(1)(x xx g -+=的定义域． 集合B 是函数][26,2,1∈-=x x y 的值域，( Ⅰ )求集合A ，B ； （本小题10分） ( Ⅱ )求)(B C A U ． （本小题5分）21．（本题15分）已知函数1)(2-++=c bx x x f 且21(=）f ． ( Ⅰ )若0b =,求函数()x f 在区间[]32-，上的最大值和最小值； （本小题8分）( Ⅱ )要使函数()x f 在区间[]32-，上单调递增，求b 的取值范围. （本小题7分）22．（本题10分）已知函数24)(2-+-=a x x x f ，1)(+-=m mx x g ( Ⅰ )若函数()y f x =在()10，上存在零点，求实数a 的取值范围； （本小题5分）( Ⅱ )当0a =时，若存在[]5,01∈x ，对于任意的[]3,22∈x都有()12()f x g x =成立，求实数m 的取值范围． （本小题5分）答案： 榆树一中2018学年高一数学第一学年期中测试卷 一选择题 ACDDBC ACCBAB二填空题 （13）2 （14） 1 （15）),2(+∞ （16）)⎢⎣⎡-21,1三解答题 17 ( Ⅰ ){}53<<=⋂x x B A( Ⅱ ) {}6,1)(≥≤=⋃x x x B A C R18( Ⅰ ) 21=a( Ⅱ ) [),10+∞∈x19 ( Ⅰ ) )-2lg()(x x g =( Ⅱ ) )4lg()(2x x F -= 4lg()(2x x F -=为偶函数20 ( Ⅰ ){}40<<=x x A {}51≤≤=y y B( Ⅱ ) {}10)(<<=⋂x x B C A u21 ( Ⅰ )10)(,1)(max min ==x f x f( Ⅱ )4≥b22 ( Ⅰ )52<<a( Ⅱ ) 127-≤≤m-----精心整理参考模板，希望对您有所帮助!!。

2017-2018学年度上学期高一期中考试数学试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，附加题20分.考试时间120分钟.第Ⅰ卷（选择题，共60分）一、选择题（每小题5分，12小题，共60分）1．已知集合}01|{2=-=x x A ，则下列式子表示正确的有（ ） ①A ∈1 ②A ∈-}1{③A ⊆φ ④A ⊆-}1,1{A ．1个B ．2个C ．3个D ．4个2．已知全集{1,2,3,4,5,6},{2,3,5},{4,5}U M N ===，则集合{1，6}= （ ）A ．MN B ．MN C ．()U C MND ．()U C MN3、下列各组函数是同一函数的是 （ ）①()f x =()g x =f(x)=x 与()g x =③0()f x x =与01()g x x=；④2()21f x x x =--与2()21g t t t =--。

A 、①② B 、③④ C 、①③ D 、①④4、函数0(1)()||x f x x x+=-的定义域是（ ）A （－∞，0）B （－∞，－1）∪（－1，0）C （0，＋∞）D （－∞，－1）∪（－1，0）∪（0，＋∞）5. 下列函数中，在定义域内既是奇函数又是增函数的是（ ）A ．y ＝e xB ．y ＝lgxC ．y ＝2x ＋1D ．y ＝x 36．如图所示，M ，P ，S 是V 的三个子集，则阴影部分所表示的集合是( )A ．(M ∩P )∩SB ．(M ∩P )∪SC ．(M ∩S )∩(∁S P )D ．(M ∩P )∪(∁V S )7．定义在R 上的函数f (x )对任意两个不相等的实数a ，b ，总有f (a )－f (b )a －b>0成立，则必有( )A ．函数f (x )先增后减B ．函数f (x )先减后增C ．f (x )在R 上是增函数D ．f (x )在R 上是减函数8．设集合A ＝{x |0≤x ≤2}，B ＝{y |1≤y ≤2}，若对于函数y ＝f (x )，其定义域为A ，值域为B ，则这个函数的图象可能是( )．9．函数lg y x =( )A ． 是偶函数，在区间(,0)-∞ 上单调递增B ． 是偶函数，在区间(,0)-∞上单调递减C ． 是奇函数，在区间(0,)+∞ 上单调递增D ．是奇函数，在区间(0,)+∞上单调递减10．已知0.1 1.32log 0.3,2,0.2a b c ===，则,,a b c 的大小关系是（ ）A ．a b c <<B ．c a b <<C ．a c b <<D ．b c a <<11．如果奇函数f (x )在区间[1,5]上是减函数，且最小值为3，那么f (x )在区间[－5，－1]上是( )A ．增函数且最小值为3B ．增函数且最大值为3C ．减函数且最小值为－3D ．减函数且最大值为－312．若f (x )是偶函数，且当x ∈[0，＋∞)时，f (x )＝x －1，则f (x －1)<0的解集是( )A ．(－1,0)B ．(－∞，0)∪(1,2)C ．(1,2)D ．(0,2)第Ⅱ卷（非选择题）二、填空题（每小题5分，4小题，共20分）13、已知函数，则f (f (－2))=_________________________14、计算()2lg5lg 2lg50+⋅＝ .15．已知幂函数)(x f y =的图象过点=)9(),2,2(f 则16、已知()()()34,1log ,1a a x a x f x x x --<⎧⎪=-∞+∞⎨≥⎪⎩是，上的增函数，那么a 的取值范围是三、解答题 （解答应写出文字说明，证明过程或演算步骤） 17．（ 10分）已知集合{|121}A x a x a =-<<+，{|01}B x x =<<，若A B =∅，求实数a 的取值范围。

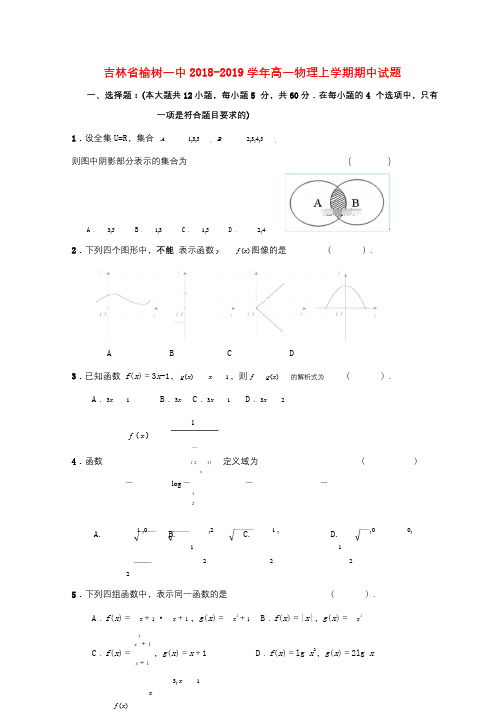
吉林省榆树一中2018-2019学年高一物理上学期期中试题一、选择题：(本大题共12小题，每小题5分，共60分．在每小题的4个选项中，只有一项是符合题目要求的)1．设全集U=R，集合A1,3,5，B2,3,4,5，则图中阴影部分表示的集合为（）A．3,5B．1,3C．1,5D．2,42．下列四个图形中，不能表示函数y f(x)图像的是( )．A B C D3．已知函数f(x)＝3x-1，g(x)x1，则f g(x)的解析式为( )．A．3x1B．3x C．3x1D．3x21f(x)4．函数(21)定义域为( )xlog121,0,21,,00,A. B. C. D.1122225．下列四组函数中，表示同一函数的是( )．A．f(x)＝x＋1·x＋1，g(x)＝x2＋1B．f(x)＝|x|，g(x)＝x22x＋1C．f(x)＝，g(x)＝x＋1 D．f(x)＝lg x2，g(x)＝2lg xx＋13,x1xf(x)x f(a)1a6. 设函数, 若, 则( )2,x1A.1或2B.0或1C.0或4D.1或47. 下列函数f(x)中，满足“对任意x1，x2∈(0，＋∞)，当x1＜x2时，- 1 -都有f(x1)＞f(x2)”的是( ).1A．f(x)＝B．f(x)＝x2 C ．f(x)＝e x D．f(x)＝ln xx8．已知定义在R上的函数f (x)的图象是连续不断的，且有如下对应值表：x 1 2 3f (x) 6.1 2.9 －3.5那么函数f (x)一定存在零点的区间是（）A. (－∞，1)B. (1，2)C. (2，3)D. (3，+∞)1x,x29．已知函数x2，则的值等于( )f(x)f(x3),x2A. B . C . D. 无意义1a2b e2c log a,b,c210. 若，，，则的大小关系是( )2A. a b c B b a c C c b a D. a c bf()m3m,1mx x11．已知函数是定义在区间上的奇函数,则( )A .B .C. D . 与大小不确定12. 已知：偶函数f(x)定义域为(-∞，0) ∪(0，+∞)且1,x(-∞，0)上有. ，若f(－1)＝0，x(1x)x22则不等式f(x)＜0的解集是( ).A．(－∞，－1)∪(0，1) B．(－∞，－1)∪(1，＋∞)C．(－1，0)∪(0，1) D．(－1，0)∪(1，＋∞)二、填空题：（本大题共4小题，每小题5分，共20分）- 2 -f x)2log(f(1)x x13．已知：函数，则21214. 计算：log lg2lg5．3315．已知：已知函数f(x)a1,(01)过定点x3a且ax3a且a(m,n)则函数f(x )x2(m1)x n的单调递增区间是．(用区间表示)16．已知奇函数f x 的定义域是2,2，对于任意有x1,x0,22(x1x)f x f x(1x)()()0x f m(m 1). ，若,2122则m的取值范围是．三、解答题：（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤）17（本题10分）设全集为R，Ax3x 6，Bx 12x 19求( Ⅰ) A B（本小题5分）( Ⅱ) C(A U B)（本小题5分）R(x ax1f)12,18. （本题10分）已知函数的图像经过点，2其中a0且a1( Ⅰ)求a的值（本小题5分）f x0( Ⅱ) 若(x)1,求的取值范围（本小题5分）19．（本题10分）已知函数f(x)lg(2x)，g(x)lg(m x)且g(1)0 ( Ⅰ)求函数g(x)的解析式；（本小题5分）- 3 -( Ⅱ)判断函数F(x)f(x)g(x)的奇偶性，并说明理由．（本小题5分）120.（本题15分）已知全集U R,集合A是函数g(lg(4x)的定义域．x)x集合B是函数y x1,x2,26的值域，( Ⅰ)求集合A，B；（本小题10分）( Ⅱ)求A(C B)．（本小题5分）U21．（本题15分）已知函数f(x)x2bx c1且f(1）2．( Ⅰ)若b0,求函数f x在区间-2，3上的最大值和最小值；（本小题8分）( Ⅱ)要使函数f x在区间-2，3上单调递增，求b的取值范围. （本小题7分）22．（本题10分）已知函数f(x)x24x a2，g(x)mx m1 ( Ⅰ)若函数f(x)在0，1上存在零点，求实数a的取值范围；（本小题5分）( Ⅱ)当a0时，若存在0,5，对于任意的2x2,31x都有f x g x成立，求实数m的取值范围．（本小题5分）1(2)- 4 -答案：榆树一中2018学年高一数学第一学年期中测试卷一选择题ACDDBC ACCBAB1二填空题（13）2 （14） 1 （15）(2,)（16）1,2三解答题17( Ⅰ) A B x3x5( Ⅱ) C(A B)x x1,x6R1a18( Ⅰ) 2( Ⅱ) 1,)x19( Ⅰ) g(x)lg(2-x)( Ⅱ) F(x)lg(4x2)F(x)为偶函数20( Ⅰ) A x0x4B y1y5( Ⅱ) A(C B)x0x1umin f x21( Ⅰ) f(x)1,()10max( Ⅱ)b422( Ⅰ) 2a57( Ⅱ) 12- 5 -。

吉林省榆树一中2017-2018学年高一数学下学期期末考试试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

试卷满分150分，考试时间120分钟。

注意事项：1）、开始答卷前，考生务必将自己的姓名、准考证号填写清楚，并贴好条形码。

请认真核准条形码上的准考证号、姓名。

2）、将选择题用2B 铅笔把答题卡上对应题目的答案标号涂黑，非选择题用0.5毫米黑色墨水签字笔将答案答在答题卡上对应的答题区域内，在试卷上作答无效。

3）、考生必须保持答题卡的整洁。

第 I 卷 （选择题共60分）一、 选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1.sin 210= （ ） A12 B 12-2.已知角α的始边在x轴非负半轴上，终边上一点的坐标是()，则tan α=（ ）BD 3.已知在空间直角坐标系中，O 是坐标原点，向量()()1,1,1,1,0,1OA OB =-=-，则AB =（ ） A 31( ) A sin 2-cos 2B cos 2-sin 2C ±(sin 2-cos 2)D sin 2+cos 25. 有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为 ( ) A13 B 12 C 23 D 346. 某中学采用系统抽样方法，从该校高一年级全体800名学生中抽50名学生做牙齿健康检查．现将800名学生从1到800进行编号．已知从33～48这16个数中取的数是39，则在第1小组1～16中随机抽到的数是 ( ) A 5 B 7 C 11 D 137. 按如图所示程序框图运算，若输出2k =,则输入的x 的取值范围是 ( ) A (28,+∞) B (-∞,57］ C (28,57］ D ［28,57)8. 已知一个小虫在边长为2的正三角形内部爬行，到各个顶点的距离不小于1时为安全区域，则小虫在安全区域内爬行的概率是 （ ）A 1 C 16π- D 6π 9. 已知点M 是直线3420x y +-=上的动点，点N 为圆()()22111x y +++= 上的动点，则|MN|的最小值是 ( )9413A B 1 C D55510.函数()()sin 0,2f x A x B πωϕωϕ⎛⎫=++><⎪⎝⎭的图象如下， 则()()()()301220182S f f f f =++++-等于 ( )A 0B 504C 1 009D 2 01810. 已知向量(2sin ,m B =，2cos 2,2cos12B n B ⎛⎫=- ⎪⎝⎭， 且m ∥n ，则锐角B 的值为 ( )AB C D 12643ππππ 12.下列说法正确的有几个 （ ） ①回归直线y bx a =+至少过散点中的某一个。

高二联考数学试卷（文科）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

试卷满分150分，考试时间120分钟。

注意事项：1）、开始答卷前，考生务必将自己的姓名、准考证号填写清楚，并贴好条形码。

请认真核准条形码上的准考证号、姓名。

2）、将选择题用2B 铅笔把答题卡上对应题目的答案标号涂黑，非选择题用0.5毫米黑色墨水签字笔将答案答在答题卡上对应的答题区域内，在试卷上作答无效。

3）、考生必须保持答题卡的整洁。

第I 卷一、选择题（本大题包括12题，每小题5分，共60分） 1.已知全集U=R ，集合A={x|-2≤x ＜0},B={x|2x-1＜14}，则()=B A C R ( ) A (-∞,-2)∪-1,+∞) B (-∞,-2］∪(-1,+∞) C (-∞,+∞) D (-2,+∞) 2.已知复数21iz i=+，则共轭复数z =( ) A 1i -+ B 1i - C 1i + D 1i --3. 设()()()2,106,10x x f x f f x x -≥⎧⎪=⎨+<⎪⎩错误！未找到引用源。

则()5f 的值为( )A 10B 11C 12D 134. 某客运部门规定甲、乙两地之间旅客托运行李的费用为：不超过25 kg 按0.5元/kg 收费，超过25 kg 的部分按0.8元/kg 收费，计算收费的程序框图如图所示，则①②处应填( )A 0.8y x =0.5y x =B 0.5y x =0.8y x =C 0.87.5y x =-0.5y x =D 0.812.5y x =+0.8y x =5. 方程ln 62x x =-的根必定属于区间( )A (-2,1)B (错误！未找到引用源。

,4)C (1,错误！未找到引用源。

)D (错误！未找到引用源。

,错误！未找到引用源。

)6. 若实数,a b 满足0a b +<，则( ) A ,a b 都小于0B ,a b 都大于0C ,a b 中至少有一个大于0D ,a b 中至少有一个小于07.设()11,x y ,()22,x y ，…，(),n n x y 是变量x 和y 的n 个样本点，直线l 是由这些样本点通过最小二乘法得到的线性回归直线(如图)，以下结论中正确的是( )A x 和y 的相关系数为直线l 的斜率B x 和y 的相关系数在0到1之间C 当n 为偶数时，分布在l 两侧的样本点的个数一定相同D 直线过l 点(x,y )8.函数()ln f x x x =的图象大致是( )A B C D9.已知函数()y f x =是可导函数，且()'12f =，则()()11limx f x f x∆→+∆-=∆( )A12B 2C 1D 1-10.若偶函数()f x 在(-∞,0)上单调递减，则不等式()()1lg f f x -<的解集是 ( ) A (0，10) B (110,10) C (110,+∞) D (0,110)∪(10,+∞)11.如图是2018年元宵节灯展中一款五角星灯连续旋转闪烁所成的三个图形，照此规律闪烁，下一个呈现出来的图形是( )A B C D12. 已知函数()f x 的定义域为R ，(2)2022f -=，对任意(,)x ∈-∞+∞，都有'()2f x x <成立，则不等式2()2018f x x >+的解集为（ ） A ．(2,)-+∞ B ．(2,2)-C ．(,2)-∞-D ．(,)-∞+∞第II 卷二、填空题（本大题包括4小题，每小题5分，共20分） 13..函数2log (1)()3x f x x -=-的定义域为．14. 已知函数()sin f x a x =且()'2f π=，则a 的值为．15.甲、乙、丙三名同学在考试中只有一名同学得了满分。

榆树一中2019—2020学年度高一上学期期中考试数学（理）试题时间 120分钟总分150分一．选择题（本题共12个小题，每个小题5分，共60分）1.已知集合A={1,2,3}，B={1,3}，则A∩B=( )A{2} B {1,2} C {1,3} D {1,2,3}2.3.4.5.函数y＝x|x|， x∈R ，满足( )A ．既是奇函数又是减函数B ．既是偶函数又是增函数C ．既是奇函数又是增函数D ．既是偶函数又是减函数6.若函数f(x)为奇函数，且当x>0时，f(x)=x−1，则当x<0时，有（）A. f(x)>0.B. f(x)<0C. f(x)f(−x) 0D. f(x)−f(−x)>07.8.若幂函数f(x)=xα在(0,+∞)上是增函数，则（）。

A. α>0B. α<0C. α=0D. 以上都不对9.函数y=a x与y=-log a x（a＞0，且a≠1）在同一坐标系中的图像形状只能是（）10.11.12. 设)(x f 是定义在),(+∞-∞上的偶函数，且它在),0[+∞上单调递增，若)2(),21(log ),31(log32-===f c f b f a ，则a,b,c 的大小关系是（ ） AC二，填空题（本题共4个小题，每个小题5分，共20分） 13. 函数f(x)=lg(2x-2)的定义域是 _______________________. 14.15.已知f(x 6)=log 2X,那么f(8)=---------16. 已知函数f(x)=log 2(4x+1)+mx ，当m>0时，关于x 的不等式f(log 3x)<1的解集为________．三，解答题（本题共6个题，共70分） 17. （本题满分10分）设集合A={x|x+m ≥ 0},B={x|−2<x<4}, 全集U=R,且(∁U B)∪A=R 求实数m 的取值范围。

高中数学学习材料马鸣风萧萧*整理制作榆树一中2016-2017学年度上学期高一期中考试数学试卷时间：120分钟，满分150分）一、选择题（本大题共12个小题，每小题5分共60分，每小题只有一个正确答案）1． 已知全集U ={0，2，4，6，8，10}，集合A ={2，4，6}，B ＝{1}，则A ∪B 等于（A ）{0，1，8，10} （B ）{1，2，4，6}（C ）{0，8，10} （D ）Φ2. 下列关系中正确的个数为①0∈{0}，②Φ{0}，③{0，1}⊆{（0，1）}.（A ）0 （B ）1 （C ）2 （D ）33. 下列四个函数,与y =x 表示同一函数的是A.y =(x )2B.y =33xC.y =2xD.y =xx 24不等式（x ＋1）（x －2）＞0的解集为（A ）{|12}x x x <->或 （B ）{|21}x x x <->或（C ）{|21}x x -<< （D ）{|12}x x -<<5下列幂函数中过点(0,0),(1,1)的偶函数是 A.21x y = B. 2x y = C. 1-=x y D.3x y =6．若函数32)2(+=+x x g ，则)3(g 的值是A ． 9B ． 7C ． 5D ． 37．下列函数中，既是奇函数又在区间（0．+∞）上单调递增的函数是A ．y= 1nxB ．y=x 3C ．y=2| x |D ．y= -x8．如图，设a,b,c,d>0，且不等于1，y=a x , y=b x ,y=c x ,y=d x 在同一坐标系中的图象如图，则a,b,c,d 的大小顺序A 、a<b<c<dB 、a<b<d<cC 、b<a<d<cD 、b<a<c<d9．已知函数f (x )=x 2+2(a －1)x +b 在区间(-∞,4］上递减,则a 的取值范围是A.［-3,+∞）B (-∞,-3] C.(-∞,5］ D.［3,+∞) 10．数x y ln 1-=的定义域为A.(]e ,0B.(]e ,∞-C. (]10,0D. (]10,∞-11.数60.7 ，0.76，log 0.76的大小顺序是A ．0.76＜log 0.76＜60.7 B. 0.76＜60.7＜log 0.76C. log 0.76＜60.7＜0.76D. log 0.76＜0.76＜60.7 12．已知0<a<1,b<-1,函数f(x)=a x +b 的图象不经过:A.第一象限;B.第二象限;C.第三象限;D.第四象限二、 填空题（本大题共4小题，每小题5分，共20分）13.若1,0≠>a a ，则函数y =a x －1+2的图象一定过定点____________。

2017-2018学年度榆树一中学校高二期中考试试题理科数学考试时间：120分钟；1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、单选题（本题共12个小题，每题5分，共60分） 1．求函数()sin cos f x a x =+的导数（ ）A. cos sin a x +B. cos sin a x -C. 0D. sin x -2．复数121ii-=+（ ） A. i B. i - C. 132i -- D. 332i-3．曲线ln y x x =在x e =处的切线方程为（ ）A. y x e =-B. 2y x e =-C. y x =D. 1y x =+ 4．复数2i 1iz -=（i 是虚数单位）在复平面内对应的点在（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 5．函数f (x )＝12x 2－ln x 的最小值为( )A.12B. 1C. 0D. 不存在 6．函数f （x ）=2x 2-4lnx 的单调减区间为A. （-1，1）B. （1，+∞）C. （0，1）D. -1，0） 7．已知函数，其导函数的图象如图，则对于函数的描述正确的是（ ）．A. 在上为减函数B. 在处取得最大值C. 在上为减函数D. 在处取得最小值8．若,则,某学生由此得出结论:若,则,该学生的推理是 ( )A. 演绎推理B. 逻辑推理C. 归纳推理D. 类比推理9．正弦函数是奇函数，f(x)＝sin(x 2＋1)是正弦函数，因此f(x)＝sin(x 2＋1)是奇函数．以上推理( ) A ．结论正确 B ．大前提不正确 C ．小前提不正确 D ．全不正确10．函数()3212f x x x =-+的图象大致是11．如图是函数()y f x =的导函数()'y f x =的图象，给出下列命题： ①-2是函数()y f x =的极值点； ②1是函数()y f x =的极值点；③()y f x =的图象在0x =处切线的斜率小于零； ④函数()y f x =在区间()2,2-上单调递增. 则正确命题的序号是（ ）A. ①③B. ②④C. ②③D. ①④ 12．设复数()211i z i-=+，则z =（ ）A. 4B. 2C.D. 1第II 卷（非选择题）二、填空题（本题共4个小题，每题5分，共20分） 13．1x =-为函数()3223f x x ax =-的一个极值点，则函数()f x 的极小值为__________． 14．计算()0cos 1x dx π+=⎰_________.15．5名工人分别要在3天中选择一天休息，不同方法的种数是____________． 16．给出下列等式：观察各式：221,3,a b a b +=+=3344554,7,11,a b a b a b +=+=+=，则依次类推可得66a b += ；四、解答题（本题共6个题，共70分）17．（本题12分）复数()()22563m m m m i -++-， m R ∈， i 为虚数单位．(I)实数m 为何值时该复数是实数； (Ⅱ)实数m 为何值时该复数是纯虚数．18．（本题12分）已知复数121i,46i z z =-=+． ⑴求21z z ； ⑵若复数1i z b =+ ()R b ∈满足1z z +为实数，求z ．19．（本题12分）若()32133f x x x x =+-， x R ∈，求： （1）()f x 的单调增区间；（2）()f x 在[]0,2上的最小值和最大值。

榆树一中2017—2018学年度高一下学期期中考试英语试题第一部分听力（1—20小题）在笔试结束后进行。

注意事项：英语听力共两节，共20小题；每小题1.5分，满分30分。

做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1.What is the woman?A. A studentB.A secretaryC. A teacher2.What does the woman say about Tom?A. He works hardB. He is cleverC.He is popular3.What are the speakers talking about?A.Where to meet Mr JacksonB.Whether to call Mr JacksonC.When to meet Mr Jackson4.How will the man go to the airport tomorrow?A. By busB.By taxiC. By car5.Where will the woman go tonight?A. A restaurant.B. A theaterC.A bar第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

每段对话或独白后有几个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。

听每段对话或独白前, 你将有时间阅读各个小题, 每小题5秒钟；听完后, 各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料, 回答第6、7题。