第五章习题--最终稿重庆大学信号与信统杨浩版答案

信号系统习题解答_3版_徐天成_南理工老师留的平时作业题信号系统习题解答_3版_徐天成_南理工老师留的平时作业题第2章习题答案 2-1 绘出下列各时间函数的波形图1 2 3 45 6解2-5 已知波形如图题2-5所示试画出下列信号的波形图图题2-53 5 解2-6 已知波形如图题2-6所示试画出下列信号的波形图图题2-64 6解2-7 计算下列各式1 2 3 4 5 6 7 8 910 11 12 解 1 原式2 原式3 原式4 原式5 原式6 原式7 原式8 原式9 原式10 原式11 原式12 原式2-8 画出图题2-8所示各信号的偶分量和奇分量的波形图题2-8解 bc已知求的表达式并画出的波形图解2-13 已知的波形如图题2-13所示求和并分别画出和的波形图图题2-13解2-14 对下列函数进行积分运算并画出积分后的波形图1 2 3解23第3章习题答案3-1 已知周期矩形脉冲信号的重复频率脉宽幅度如图题3-1所示用可变中心频率的选频回路能否从该周期矩形脉冲信号中选取出512205080及频率分量来要求画出图题3-1所示信号的频谱图图题3-1解频谱图为从频谱图看出可选出52080kHz的频率分量3-3 求图题3-3 所示周期锯齿信号指数形式的傅里叶级数并大致画出频谱图图题3-3解在一个周期0T1内的表达式为傅氏级数为频谱图为3-4 求图题3-4 所示半波余弦信号的傅里叶级数若大致画出幅度谱图题3-4解由于是偶函数所以展开式中只有余弦分量故傅氏级数中另由图可知有直流分量在一个周期内的表达式为其中所以的三角形式的傅里叶级数为3-6 利用信号的对称性定性判断图题3-6中各周期信号的傅里叶级数中所含有的频率分量图题3-6解 a 为偶函数及奇谐函数傅氏级数中只包含奇次谐波的余弦分量b 为奇函数及奇谐函数傅氏级数中只包含奇次谐波的正弦分量c 为偶谐函数而且若将直流分量12去除后为奇函数所以傅氏级数中只包含直流以及偶次谐波的正弦分量d 为奇函数傅氏级数中只包含正弦分量e 为偶函数及偶谐函数傅氏级数中只包含直流以及偶次谐波的余弦分量f 为奇谐函数傅氏级数中只包含奇次谐波分量3-7 已知周期函数前四分之一周期的波形如图题3-7所示根据下列各种情况的要求画出在一个周期的波形1是偶函数只含有直流分量和偶次谐波分量2是偶函数只含有奇次谐波分量3是偶函数含有直流分量偶次和奇次谐波分量解1由画出在内的波形由在内的波形及是偶谐函数它在内的波形与它在内的波形相同它在内的波形与它在内的波形相同根据上述分析可画出在内的波形按上述类似的方法可画出2和3233-8 求图题3-8 所示半波余弦脉冲的傅里叶变换并画出频谱图图题3-8解法一按定义求由于是偶函数所以化简得解法二利用卷积定理求设则于是而故的频谱是将矩形脉冲的频谱分别向左右移动幅度乘以后叠加的结果3-10 求图题3-10所示的傅里叶逆变换图题3-10解ab3-13 求函数的傅里叶变换解利用对偶性求因为所以令则即F3-15 对图题3-15所示波形若已知利用傅里叶变换的性质求图中和的傅里叶变换图题3-15解已知F3-21 已知三角脉冲信号如图题3-21 a 所示试利用有关性质求图题3-21 b 中的的傅里叶变换图题3-21解设F则F而FF3-23 利用傅里叶变换的微分与积分特性求图题3-23所示信号的傅里叶变换图题3-23解33-25 若已知利用傅里叶变换的性质求下列信号的傅里叶变换 2 4 5解2FF4F5FF3-29 根据附录B中给出的频谱公式粗略地估计图题3-29所示各脉冲的频带宽度图中时间单位为图题3 -29解a若时间单位为则频带为MHz即250KHzb若时间单位为则频带为MHz即250KHzd若时间单位为则频带为1 MHzf频若时间单位为则带为MHz即500KHz 3-32 周期矩形脉冲信号如图题3-32所示 1求的指数形式的傅里叶级数并画出频谱图 2求的傅里叶变换并画出频谱图图题3-32解 1指数形式的傅里叶级数为频谱图如下图所示图中2F频谱图为3-33 求下列函数的拉氏变换设1 46 8解14683-35 求下列函数的拉氏变换注意阶跃函数的跳变时间 1 2 3 解1233-39 求下列函数的单边拉普拉斯逆变换 3 4 7解3473-40 试利用拉氏变换的时域卷积定理求下列拉氏变换的原函数1解所以3-43 分别求下列函数的逆变换之初值和终值 1 3 解13第4章习题答案4-2 已知系统微分方程相应的齐次方程为 1试求两系统的零输入响应并粗略画出波形解124-3 给定系统微分方程起始状态及激励信号分别如下试判断系统在起始点是否发生跳变并据此写出的值123解 1因为方程在t 0时存在冲激作用则起始点会发生跳变设得a 32因为方程在t 0时存在冲激作用则起始点会发生跳变设得a 053因为方程在t 0时存在冲激和冲激偶作用则起始点会发生跳变设4-4 给定系统微分方程为若激励信号与起始状态为以下二种情况时分别求它们的全响应并指出其零输入响应零状态响应自由响应和强迫响应各分量应注意在起始点是否发生跳变12解1齐次解特解完全解因为方程在t 0时存在冲激作用则起始点会发生跳变设得a 1则完全解设零输入响应为则自由响应强迫响应152微分方程右边为原方程为由上述微分方程可知t 0后方程右边没有输入因此系统没有强迫响应完全响应和自由响应相同零输入和零状态响应的形式均为齐次解形式且零输入响应同1为零状态响应的形式为设得a 1则4-6 一线性时不变系统在相同的起始状态下当输入为时全响应为当输入为2时全响应为求输入为4时的全响应解系统的零状态响应为当输入为4x t 时系统的全响应为4-7 系统的微分方程由下列各式描述分别求系统的冲激响应与阶跃响应1解1首先求阶跃响应原方程变为方程右边没有冲激作用则起始点不会发生跳变特征方程齐次解特解B,05则代入初始值系统的阶跃响应为系统的冲激响应为4-12 一线性时不变系统当激励信号为时全响应为当激励信号为时全响应为求系统的冲激响应两种激励下起始状态相同解式 1 –式 2 得上式求导设代入上式方程两边函数相等4-13 试求下列各函数与的卷积13解134-14 对图题4-14所示的各组信号求二信号的卷积并绘出的波形解a4-15 已知分别求和画出和的波形并比较二者的区别解4-16 对图题4-16所示的各组信号求二信号的卷积并绘出的波形图题4-16 解d4-17 图题4-17所示系统是由几个子系统组合而成的各子系统的冲激响应分别为试求总系统的冲激响应并画出的波形图题4-17解第5章习题答案5-1 图题5-1所示RC电路中当t 0时开关S闭合求输出信号输入信号分别为以下几种情况1 3 4图题5-1解1345-3 电路如图题5-3所示当t 0时电路元件无储能当t 0时开关闭合求电压的表达式并画出的波形图题5-3解电流源电流为5-6 系统的微分方程为初始状态为若激励为1试用拉氏变换分析法求全响应2分别求零输入响应和零状态响应然后叠加得全响应解5-7 电路如图题5-7所示已知当t 0时开关S打开电路已达稳态设当t 0时开关S闭合求时的和图题5-7解5-10 当F s 的一阶极点落于图题5-10所示s平面中各方框所处位置时画出对应的f t 的波形填入方框中图中给出了示例此例极点实部为正波形是增长振荡解画图5-12 求图题5-12所示各网络的电压转移函数在s平面画出其零极点分布若激励信号为冲激函数 t 求响应并画出波形图题5-12解 ac5-14 写出图题5-14所示各梯形网络的电压转移函数在s平面示出其零极点分布图题5-14解 ab零极点图与a相同略d零点为0 4阶极点为5-15 已知策动点阻抗函数分别为下列各式试画出对应的电路图 1 2 34 5 6解即电路中电流源作为激励信号而电路中的电压作为响应信号 1 2 3 4 5 6 5-19 已知系统的阶跃响应为为使其零状态响应为求激励信号解5-20 某系统的起始状态一定已知输入时全响应为输入时全响应为试求输入时的全响应解5-24 如图题5-24所示电路已知激励信号为求响应并指出响应中的强迫分量自由分量暂态分量与稳态分量各分量题图5-24解所以响应为是自由响应是强迫响应是暂态响应稳态响应为05-29 给定的零极点分布如图题5-29所示令s沿j 轴移动由矢量因子之变化分析频响特性粗略绘出幅频与相频特性曲线解abcdef5-30 若的零极点如图题5-30所示试讨论它们分别是哪种滤波网络低通高通带通带阻并绘出各自的幅频特性曲线解abcdefgh5-35 图题5-35所示格形网络写出电压转移函数设在s平面画出H s 零极点分布图指出是否为全通网络在网络参数满足什么条件下才能构成全通网络题图5-35解极点为零点为当网络参数满足时系统为全通系统5-37 求图题5-37所示各流图的增益图题5-37解b5-38 试绘出下列微分方程描述的系统直接形式的模拟框图或信号流图2解25-39 用级联形式和并联形式模拟上题的系统并画出方框图解2和系统的级联形式的方框图为系统的并联形式的方框图为或用各自的信号流图表示为级联并联5-41 图题5-41所示反馈电路中是受控源 1求电压转移函数 2k满足什么条件时系统稳定图题5-41解1而所以2要使系统稳定对于二阶系统只要分母多项式各次系数非负即k 3第6章习题答案6-1 已知现用的时间间隔对其进行理想采样 1画出的波形图 2求并画出频谱图解12FF6-2 已知三角脉冲信号的频谱见附录B求图题6-2中各脉冲被冲激采样后信号的频谱并大致画出频谱图采样间隔图题6-2解ab6-3 确定下列信号的奈奎斯特采样率与奈奎斯特间隔 1 2 3 4解1F所以的最高角频率为这样奈奎斯特取样率为或奈奎斯特间隔2由于信号自乘频带展宽一倍3与叠加最高频率同4 由于的最高角频率为而的最高角频率展宽一倍即又的最高角频率为所以的最高角频率为这样6-4 已知某系统如图题6-4所示输入信号理想低通滤波器的频响特性为 1求并画出频谱图2画出的频谱图3求输出的表达式解123根据F以及F可得6-5 已知带限信号的频谱函数如图题6-5 a 所示试画出当通过图题6-5 b 所示系统时在系统中ABCD各点信号的频谱图图题6-5 b 中两个理想滤波器的频响特性分别为图题6-5解6-6 对于图64-6所示的抑制载波调幅信号的频谱由于的偶对称性使在和左右对称利用此特点可以只发送如图题6-6所示的信号的频谱称为单边带信号以节省频带试证明在接收端用同步解调的方法可以恢复原信号证明同步解调就是使单边带信号在时域上乘以在频域上则是与卷积幅度上乘以卷积结果如下图所示从此图可以看到卷积结果得到了原信号和一载频为的单边带信号再利用一低通滤波器滤除载频为的单边带信号后就得到了原信号6-12 电路如图题6-12所示写出系统频率响应特性为得到无失真传输元件参数应满足什么关系图题6-12解由电路图得可见为了得到无失真传输应有也即这样所以满足无失真传输的条件6-14 一个理想低通滤波器的网络函数为其幅频特性与相频特性如图题6-14所示试证明此滤波器对于和的响应是相同的图题6-14证明设则因为式中所以因此故两者响应一样即F6-18 图题6-18所示系统中为理想低通特性即 1若为单位阶跃信号写出的表达式2若写出的表达式解1由图知直接加在滤波器上的信号是因为而理想低通滤波器的阶跃响应为所以响应为2若则因此的频带范围限制在内最高频率又的截止频率故对是无失真传输从而有第7章习题答案7-1 分别绘出下列各序列的图形1 2 3 4解7-2 分别绘出下列各序列的图形1 2 3 4解7-3 分别绘出下列各序列的图形1 2解7-5 序列x[n]如图题7-5所示把x[n]表示为 [n]的加权与延迟之线性组合图题7-5解7-7 求下列序列的z变换X z 并注明收敛域绘出X z 的零极点图1u[n] [n] 4 u[n] u[n8] 5 [n] [n2]解7-8 求双边序列的变换标明收敛域及绘出零极点图7-11 画出X z 的零极点图三种收敛域下哪种情况对应左边序列哪种情况对应右边序列哪种情况对应双边序列并求各对应序列2 2 05 305 2解1 当时为右边序列2 当时为左边序列3 当时为双边序列7-13 已知X z1确定与X z 有关的收敛域可能有几种情况画出各自的收敛域图2求以上各种收敛域3以上序列中哪一种存在傅氏变换1收敛域可能有三种情况2对应的序列分别为3序列的收敛域包括单位圆所以此序列存在傅氏变换7-14 已知X z 若收敛域分别为1 2和2 3两种情况求对应的逆变换7-21 利用卷积定理求y[n] x[n] h[n]已知3x[n] RN[n] u[n] u[nN]h[n] anu[n]0 a 1解3根据卷积定理得由于均为因果序列因此亦为因果序列根据移位性质可求得7-24 计算下列序列的傅里叶变换n] 3 [42n] 解第8章习题答案8-2 列出图题8-2所示系统的差分方程指出其阶次图题8-2解二阶8-3 列出图题8-3所示系统的差分方程已知边界条件y[1] 0分别求以下输入序列时的输出y[n]并绘出其图形用逐次迭代方法求1 2 图题8-3 解1 28-7 求解下列差分方程的完全解1 2解1方程齐次解为特解为代入原方程完全响应为代入得2方程齐次解为特解为代入原方程完全响应为代入得8-12 用单边变换解下列差分方程y[n] 01y[n1] 002y[n2] 10u[n]y[1] 4y[2] 62y[n] 09y[n1] 005 u[n]y[1] 1 3y[n] 2y[n1] n2 u[n]y[0] 1解 2差分方程两边同时进行z变换3由差分方程得差分方程两边同时进行z变换8-13 若描述某线性时不变系统的差分方程为y[n] y[n 1] 2y[n 2]x[n] 2x[n 2]已知y[1] 2y[2] 12x[n] u[n]求系统的零输入响应和零状态响应解差分方程两边同时进行Z变换8-16 对于差分方程yy[n 1] x[n]所表示的离散系统1求系统函数H z 及单位样值响应h并说明系统的稳定性2若系统起始状态为零 10 u[n]求系统的响应y系统的收敛域不包括单位圆所以不稳定8-19 因果系统的系统函数H z 如下试说明这些系统是否稳定1 2 3 4解1收敛域为包括单位圆所以稳定2收敛域为不包括单位圆所以不稳定3收敛域为不包括单位圆所以不稳定4收敛域为不包括单位圆所以不稳定8-20 已知系统函数H z 分别在 10及05 10两种收敛域情况下系统的单位样值响应并说明系统的稳定性与因果性系统是因果不稳定的系统是非因果稳定的8-21 建立图题8-21所示各系统的差分方程并求单位样值响应h[n] 图题8-21解ab8-23 如下各序列中x[n]是系统的激励序列h[n]是线性时不变系统的单位样值响应分别求出各响应y[n]画出y[n]的图形用卷积方法1x[n] h[n]如图题8-23 a 所示 2x[n] h[n]如图题8-23 b 所示 3且图题8-23解1238-24 已知线性时不变系统的单位样值响应h[n]和输入x[n]分别如下所示求输出序列y[n]并绘出y[n]的图形1 3解138-25 图题8-25所示的系统包括两个级联的线性时不变系统它们的单位样值响应分别为h1[n]和h2[n]已知令1按下式求y[n]y[n] x[n] h1[n] h2[n] 2按下式求y[n]y[n] x[n] h1[n] h2[n] 注以上两种方法的结果应该相同卷积结合律解128-27 用计算机对测量的随机数据进行平均处理当收到一个测量数据后计算机就把这一次输入数据与前三次输入数据进行平均试求这一运算过程的频率响应则本次与前三次数据的平均值为对上式进行z变换得8-28 利z平面零极点作图法画出下列系统函数所对应系统的幅1H z 2H z 3H z解 1238-29 已知横向数字滤波器的结构如图题示试以M 8为例写出差分方2求系统函数H z 3求单位样值响应h4画出H z 的零极点图5粗略画出系统的幅频特性图题8-29解7阶为保证系统稳定设 1则零极点图如下8-36 由下列差分方程画出离散系统的结构图求系统函数H z 及单位样值响应hy[n] 6y[n 1] x [n] 2y[n] x[n] 5x[n 1]8x[n 2]3y[n] 3y[n 1] 3y[n 2] y[n 3] x [n]4y[n] 5y[n 1] 6y[n 2] x [n] 3x[n 2]解8-37 已知某离散系统的系统函数为H z m为常数1写出对应的差分方程 2画出该系统的结构图3求系统的频率响应特性并画出m 0 05 1三种情况下系统的幅频特性与相频特性曲线28-38 画出系统函数H z 所表示的系统的级联和并联形式结构图 2并联形式第9章习题答案9-1 建立图题9-1所示电路的状态方程图题9-1解b9-2 建立图题-2所示电路的状态方程若指定输出为 R2上的电压图题9-2 解b9-4 将图题-4 a 所示系统画成流图形式并列写系统的状态方程和输出方程9-4解a9-5 系统为如图题9-5所示的方框图试列写状态方程和输出方程图题9-5 解9-7 给定系统的状态方程和起始条件为求解该系统9-10 系统的状态方程和输出方程为且已知 1 0 1 2 0 1x t u t1求系统函数矩阵H s 2求输出y t 解9-12 一离散系统如图题-12所示1当输入x[n] [n]时求 1[n] 2[n]和h[n]2列系统的差分方程129-13 系统的状态方程和输出方程为已知1画出模拟框图和信号流图2求系统函数Hz 3求解1231tf1t 321tf2t 105tf3t 11π2π图题3-7tS t图题4-140 t 1 2 1t s 1 0 t 2 4 1 t s 2tS t 312ab4 3ab4 -1153-3-5tv2 t 0 jtv2 t 0jjajci tv t 1F 1Hi tv t 1 1Hi tv t 1F1Hi t v t 1 1Fi t v t 1 1H1Fi t v t 1 1HjH j 0jH j 0jH j1jH j1jH j1jH j1jH j 0低通滤波器jH j 0带通滤波器jH j 0高通滤波器jH j 0带通滤波器带通滤波器jj 0j 0H j 0带阻滤波器jj 1j 1 j 2j 2H j 02高通滤波器jj 0j 0H j 0带阻滤波器jj 1j 1 j 2 j 2H j21s 1 s 1 3s 1322XsYs1s 1 s 1 s 1 32XsYs321s 1 s 12s 1112XsYs1s 1 s 1111s 12Xs2Yss 1 s 1 s 1112XsYs2s 1 s 111s 12XsYs21t图题6-4 图题6-6 02 0 2 0 m2 0 m 2 0F1 j 图题6-18 12Re zjIm z 14Re zjIm z 1272Re z jIm z jIm z 122Re z 2z 2Re z jIm z 12z 12Re z jIm z 12 z 2 jIm z Re z 图题8-25 Re z jIm z 0051ωωH ejω 223Re z jIm z051ω223ωH ejω 0ω-05 01Re z jIm z H ejω ω320571Re z jIm z x [n] 213y [n] -58x [n] y[n] x[n] y [n] 3 -3x[n] y[n] -35-6mx[n] y[n] ω 1ωφ ωa 0223π2πω13ππ6-π6 π2πωφ ωb 05π2πωωφ ω π2ππ2-π2 0c 3-5102-5x[n] y[n] 2 x[n] y[n] 2 -5图题9-12。

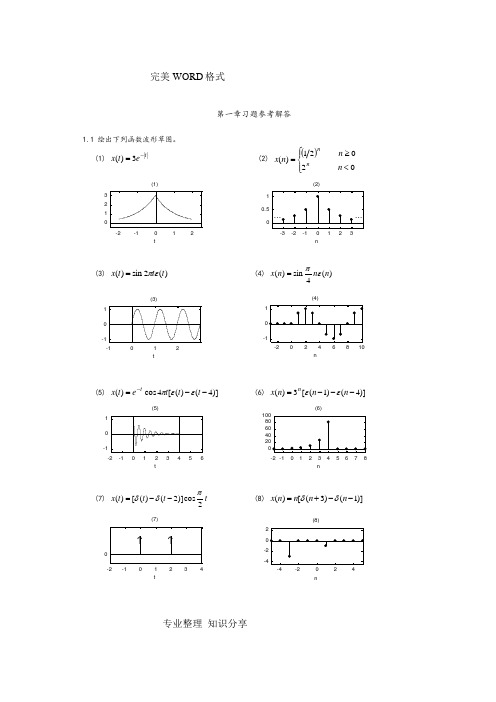
完美WORD 格式专业整理 知识分享第一章习题参考解答1.1 绘出下列函数波形草图。

(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n(3) )(2sin )(t t t x επ=(4) )(4sin )(n n n x επ=(5) )]4()([4cos )(--=-t t t et x tεεπ(6) )]4()1([3)(---=n n n x nεε(7) t t t t x 2cos)]2()([)(πδδ--=(8) )]1()3([)(--+=n n n n x δδ完美WORD 格式专业整理 知识分享(9) )2()1(2)()(-+--=t t t t x εεε(10) )5(5)]5()([)(-+--=n n n n n x εεε(11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε(13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率，并指出是能量信号还是功率信号，或两者均不是。

(1) ||3)(t et x -=解 能量有限信号。

信号能量为：()⎰⎰⎰⎰∞-∞-∞∞--∞∞-+===02022||2993)(dt edt edt e dt t xE ttt ∞<=⋅-⋅+⋅⋅=∞-∞-9)21(92190202tte e(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。

信号能量为：()∞<=+=+==∑∑∑∑∑∞=--∞=∞=--∞=∞-∞=35)41(4])21[(2)(0102122n n n nn n n n n n xE(3) t t x π2sin )(=完美WORD 格式专业整理 知识分享 解 功率有限信号。

周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率，t π2sin 的周期为1。

第5章连续时间信号的抽样与量化5.1试证明时域抽样定理。

证明：设抽样脉冲序列是一个周期性冲激序列，它可以表示为T(t)(tnT)sn由频域卷积定理得到抽样信号的频谱为：1F s ()F()T 2()1 T snFns式中F()为原信号f(t)的频谱，T ()为单位冲激序列T (t)的频谱。

可知抽样后信 号的频谱()F 由F()以s 为周期进行周期延拓后再与1T s 相乘而得到，这意味着如果 s s2，抽样后的信号f s (t)就包含了信号f(t)的全部信息。

如果s2m ，即抽样m 间隔 1 Tsf2m，则抽样后信号的频谱在相邻的周期内发生混叠，此时不可能无失真地重建 原信号。

因此必须要求满足1 Tsf2 m，f(t)才能由f s (t)完全恢复，这就证明了抽样定理。

5.2确定下列信号的最低抽样频率和奈奎斯特间隔：2t （1）Sa(50t)（2）Sa(100)2t （3）Sa(50t)Sa(100t)（4）(100)(60)SatSa解：抽样的最大间隔 T s 12f 称为奈奎斯特间隔，最低抽样速率f s 2f m 称为奈奎m斯特速率，最低采样频率s 2称为奈奎斯特频率。

m（1）Sa(t[u(50)u(50)]，由此知m50rad/s ，则50)5025 f ， m由抽样定理得：最低抽样频率50 f s 2f m ，奈奎斯特间隔1 T 。

sf50s2t（2）)Sa(100)(1100200脉宽为400，由此可得radsm200/，则100f，由抽样定理得最低抽样频率m200f s2f m，奈奎斯特间隔1T。

sf200s（3）Sa[(50)(50)]，该信号频谱的m50rad/s(50t)uu50Sa(100t)[u(100)u(100)],该信号频谱的m100rad/s10050Sa(50t)Sa(100t)信号频谱的m100rad/s,则f，由抽样定理得最低m抽样频率100f s2f m，奈奎斯特间隔1T。

1、序列 f(n)=cos(πn/2)[ξ(n?2)?ξ(n?5)]的正确图形是（）。

•A、•B、•C、•D、•A、H(s)的零点•B、H(s)的极点•C、系统的输入信号•3、信号f1(t),f2(t)波形如图所示，设f(t)=f1(t)*f2(t)，则f(0)为（）•A、1•B、2•C、3•4、积分等于（）•A、•B、•C、•D、5、积分等于（）•A、•B、•C、•D、6、信号f1(t),f2(t)波形如图所示，设f(t)=f1(t)*f2(t),则f(0)为（）•A、0•B、1•C、2•7、信号f1(t) 和 f2(t)分别如图(a)和图(b)所示，已知 [f1(t)]=F1(jω)，则f2(t)的傅里叶变换为（）•A、•B、•C、•D、•A、f（-2t）右移5•B、f（-2t）左移5•C、f（-2t）右移5/2•9、连续周期信号的频谱有( )。

•A、连续性，周期性•B、连续性，收敛性•C、离散性，周期性•10、若系统的起始状态为0，在x（t）的激励下，所得的响应为———（）•A、强迫响应•B、稳态响应•C、暂态响应•11、已知信号f(t)的傅里叶变换F(jω)=δ(ω?ω0)，则 f(t)为（）•A、e jw0t /2π•B、12πe?jw0t•C、12πejw0tξ(t)•12、已知 f(t)，为求f(t0-at) 应按下列哪种运算求得正确结果？（式中t0,a 都为正值）（）。

•A、f(at) 右移t0•B、f(at) 右移t0•C、f(at) 左移t0/a•13、下列论断正确的为（）。

•A、两个周期信号之和必为周期信号•B、非周期信号一定是能量信号•C、能量信号一定是非周期信号•14、连续信号f(t)与δ(t?t0)的卷积，即f(t)*δ(t?t0)=（）。

•A、f(t)•B、f(t-t0)•C、δ(t)•15、信号 f(t)=e2tξ(t)的拉氏变换及收敛域为（）•A、•B、•C、•D、16、若序列f(n)的图形如图（a）所示，那么f(-n+1)的图形为图（b）中的（）•A、。

重庆大学测试技术习题详解第二章习题解答2-1．什么是信号？信号处理的目的是什么？2-2．信号分类的方法有哪些？22-3．求正弦信号某tAint的均方值某。

解：1T21T22某tdtAintdtT0T022T22T1co2t2AintdtAdt00TT222TinTA2AT4422某A2也可先求概率密度函数：p(t)则：某p(某)d某222A某2某22-4．求正弦信号某tAin(t)的概率密度函数p(某)。

某dt1,Ad某某()2A解：tarcinA某22代入概率密度函数公式得：p(某)limt12dt12lim某0某某0TTA2某2d某T21222A2某2A某2-5．求如下图所示周期性方波的复指数形式的幅值谱和相位谱某-T解在某(t)的一个周期中可表示为t-T1T1T1某(t)tT1T1tT2该信号基本周期为T，基频0=2/T，对信号进行傅里叶复指数展开。

由于某(t)关于t=0对称，我们可以方便地选取-T/2≤t≤T/2作为计算区间。

计算各傅里叶序列系数cn当n=0时，常值分量c0：c0a0当n0时，2T11T1dtTT1TT1T1cn最后可得1T1jn0t1jn0tedteTT1jn0Tejn0tejn0tcnn0T2j2cn其幅值谱为：cn注意上式中的括号中的项即in(n0T1)的欧拉公式展开，因此，傅里叶序列系数cn可表示为2in(n0T1)2inc(n0T1)，n0n0TT2T1inc(noT1)，相位谱为：n0,,频谱图如下：TCn2T1/T/T100Cn2T1/T/T100n02-6．设cn为周期信号某(t)的傅里叶级数序列系数，证明傅里叶级数的时移特性。

即：若有FS某tcnFS则某tt0e'cnj0t0cn证明：若某(t)发生时移t0（周期T保持不变），即信号某(t-t0)，则其对应的傅立叶系数为TT某tej0tdt令tt0，代入上式可得'cnT某eTj0(t0)dd1Tej0t0cnej0t0因此有某eTj0FS某tt0ej0t0cnej(2/T)t0cn同理可证FS某tt0ej0t0cnej(2/T)t0cn证毕！2-7．求周期性方波的（题图2-5）的幅值谱密度解：周期矩形脉冲信号的傅里叶系数Cn2T11Tjn0tedtinc(n0T1)T1TT则根据式，周期矩形脉冲信号的傅里叶变换，有某()22T1inc(n0T1)(n0)nT此式表明，周期矩形脉冲信号的傅里叶变换是一个离散脉冲序列，集中于基频0以及所有谐频处，其脉冲强度为4T1/T0被inc(t)的函数所加权。

目　录2014年重庆大学841信号与系统考研真题2013年重庆大学841信号与线性系统考研真题2012年重庆大学841信号与系统考研真题2010年重庆大学842信号与线性系统考研真题及详解2009年重庆大学842信号与线性系统考研真题2008年重庆大学842信号与线性系统考研真题2007年重庆大学443信号与线性系统考研真题2006年重庆大学443信号与线性系统考研真题2005年重庆大学450信号与系统考研真题2004年重庆大学450信号与系统考研真题2003年重庆大学450信号与系统考研真题2002年重庆大学591信号与线性系统考研真题2001年重庆大学555信号与线性系统考研真题2000年重庆大学103信号与线性系统考研真题2014年重庆大学841信号与系统考研真题重庆大学2014年硕士研宪生入学考属械题科目代码；四1科目名称：信号与系统总分：150分特别提醒：所有答案一律写在答题纸上，直接写在试题或草稿纸上的无效，-、(每小瞻10分，共计SQ分)回答下列问题1.戮性时不变系统具有哪些特性？最基本的特性是什么,为什么？2.什么坦。

一状态和S状态？系统有无起始点的跳变量(即从0.到3,状态的转换)怎么判断？3.什农是理想抽样？何为奈童斯特(Nyquist)额率？简述时域抽样定理’4.一个因果稳定系统，其零极点是否都在左半E平面？为什久？5.如果己知电路结构和参数，如何直观列写状态方程，堵写出一般步骤，二、(】5分)已知某线性时不变系统，激励为勺*)=m(r)时，零状态响应匕(*)如图1所示"若激励为如图2所示曲)时,试用时域法计算：(1)单位冲激响应M，｝：<2)零状态响应r(r)；(3)画出零状态畴应波形*2 [卜W)A_,2-]，的)0123401234图1&2三'(】S分)周期单位冲激序列为(0=££*-耳7；)的波形如图3所示.试求:(1)为。

重庆大学《841信号与系统》例题1-1 已知等概独立的二进制数字信号的信息速率为2400 bit/s 。

(1) 求此信号的码速率和码元宽度；(2) 将此信号变为四进制信号，求此四进制信号的码速率、码元宽度和信息速率。

解 (1) R B =R b /log 2M =(2400/log 22)Bd=2400 BdT =BR 1=24001 s=0.42 ms(2) R B =(2400/log 24)Bd=1200 Bd T=BR 1=12001 s=0.83 ms R b =2400 b/s 1-2 进制离散信源输出四个独立符号A 、B 、C 、D 。

(1) A 、B 、C 、D 出现的概率分别为41、81、81、21，求A 、B 、C 、D 每个符号所携带的信息量和信源熵； (2) A 、B 、C 、D 等概，求信源熵。

解 (1) 根据式(1.4-3)，有 =)(A I (-log241)bit=2 bit ==)()(C I B I (-log 281)bit=3 bit =)(D I (-log 221)bit=1 bit 根据式（1.4-9），有H (X )=（41×2+818×3+81×3+21×1）bit/符号=143bit/符号 (2) 根据式(1.4-9)，有H (X )=(log 24)bit/符号=2 bit/符号1-3、一个由字母A ，B ，C ，D 组成的字。

对于传输的每一个字母用二进制脉冲编码，00代替A ，01代替B ，10代替C ，11代替D 。

每个脉冲宽度为5ms（1）不同的字母是等概率出现时，试计算传输的平均信息速率。

（2）若每个字母出现的概率为P A =1/5, P B =1/4, P C =1/4, PD =3/10,试计算传输的平均信息速率。

解：首先计算平均信息量。

(1) H=-ΣP(x i )log 2 P(x i ) =441log )41(2?-?=2bit/字母平均信息速率=s /200bit /5m s 2/2=?字母字母bit(2) H= -ΣP(x i )log 2 P(x i ) =1.985 bit/字母平均信息速率=s /bit .198/5ms 2/985.1=?字母字母bit 3-1 计算机终端通过电话信道传输计算机数据，电话信道带宽为3.4 kHz ，信道输出的信噪比S/N=20 dB 。