当前位置：文档之家 › 第十、十一章 动荷载和循环应力概述

第十、十一章 动荷载和循环应力概述

  • 格式：ppt
  • 大小：1.96 MB
  • 文档页数：52

下载文档原格式

  / 52

合集下载

材料力学 第十章 动载荷

材料力学 第十章 动载荷

a t
max
m
max 2 m 2 a
min 0
r0
a
t
（3）静应力：如拉压杆
max min m
a 0
r 1
（4）非对称循环：

a 0
max min m t
max min 0 max min a
第二节 交变应力的循环特性和应力幅值
应力循环:一点的应力由某一数值开始，经过一次完整的变 化又回到这一数值的一个过程。

a
m
T
1.最大应力： max
2.最小应力： min
min
max
t 5.循环特性：
3.平均应力：
m
max min
2
4.应力幅：
a
max min
疲劳极限或有限寿命持久极限：
材料在规定的应力循环次数N下，不发生疲劳破环的最大 应力值，记作 rN ( rN ) 。 无限寿命疲劳极限或持久极限 r ： 当 max 不超过某一极限值，材料可以经受“无数次”应力 循环而不发生破坏，此极限值称为无限寿命疲劳极限或持久极限。
疲劳失效特点 a、在交变应力下构件破坏时，最大应力不仅低于材料强 度极限和屈服极限，甚至低于比例极限； b、在交变应力作用下，构件破坏前，总是要经历若干次 应力重复；而且即使是塑性很好的材料，在经历若干次应力 重复后，也会像脆性材料一样突然断裂，断裂前没有明显的 塑性变形。 c、疲劳破坏的断口存在三个区域： 疲劳源区——在光滑区内有以微裂纹 起始点，又称为裂纹源（①区域）为中心 并逐渐扩展的弧形曲线； 疲劳扩展区——又称为光滑区（②区 域），有明显的纹条，类似被海浪冲击后 的海滩，它是由裂纹的传播所形成；

第十一章动载荷

第十一章动载荷

第十一章 动载荷一、基本内容1. 动载荷的基本概念极其分类;2. 动静法及其应用。

3. 工程中的冲击问题。

4. 构件受冲击时的应力与变形计算 二、教学目的１．了解动载荷的基本概念极其分类。

２．掌握动静法的应用３．会计算构件作匀加速运动、匀角速度转动时的强度。

４．掌握动动载系数的计算方法。

５．了解构件受冲击时的动应力与动变形的概念。

６．会计算落体冲击与水平冲击作用时的动载系数 三、重点和难点重点掌握动载荷的基本概念、动载系数的概念重点掌握动载系数的计算了解构件受冲击时的应力与变形计算。

难点是各种条件下的动载系数的计算方法四、典型例题分析例 一钢索起吊重物如图13-1，以等加速度 a 提升。

重物M 的重力为 P ，钢索的横截面积为A ，钢索的重量与 P 相比甚小而可略去不计。

试求钢索横截面上的动应力 d 。

解：钢索除受重力 P 作用外，还受动载荷（惯性力）作用。

根据动静法，将惯性力a gP加在重物上，这样，可按静载荷问题求钢索横截面上的轴力 d N 。

由静力平衡方程：0=--a gPP N d 解得)1(ga P a g P P N d +=+= 从而可求得钢索横截面上的动应力为：st d st d d k gag a A P A N σσσ=+=+==)1()1( 其中APst =σ 是P 作为静载荷作用时钢索横截面上的应力，ga k d +=1 是动荷系数。

对于有动载荷作用的构件，常用动系数 d k 来反映动载荷的效应。

此时钢索的强度条件为][σσσ≤=st d d K 其中 ][σ 为构件静载下的许用应力。

例 图13-2中一平均直径为 D ，壁厚为 t 的薄壁圆环，绕通过其圆心且垂直于环平面的轴作均速转动。

已知环的角速度 ω ，环的横截面积 A 和材料的容重 γ ，求此环横截面上的正应力。

解：因圆环等速转动，故环内各点只有向心加速度。

又因为 D t << ，故可认为环内各点的向心加速度大小相等，都等于22ωD a n =沿环轴线均匀分布的惯性力集度 d q 就是沿轴线单位长度上的惯性力，即：221ωγγgD A a g A q n d =⋅⋅=上述分布惯性力构成全环上的平衡力系。

第十章-动载荷

第十章-动载荷
2 动载荷问题分类
2
2 动载荷问题分类 1) 构件有加速度时旳应力计算; 2) 冲击问题； 3) 振动问题； 4) 交变载荷。
3
§10. 2 动静法旳应用
1 动静法
即为理论力学中简介旳达朗伯原理。
2 匀加速平动构件中旳动应力分析
例子 设杆以匀加速度a作平动，
b
R
aR
截面积为A，比重为 。
加上惯性力系。
3 求解冲击问题旳能量法 线弹性系统
任一线弹性杆件或构造都可简化为线性弹簧。 15
3 求解冲击问题旳能量法 线弹性系统
任一线弹性杆件或构造都可简化为线性弹簧。
l Pl EA
P EA l l
等价弹簧旳弹性
系数 k EA
l
16
l Pl EA
等价弹簧旳弹性系数 能量法
P EA l l
k EA l
工程实例 气缸
在满足刚度和强度要求旳前提下
28
冲击问题旳一般解题环节
1) 判断是垂直冲击还是水平冲击；
2) 求 △st ； 3) 求 Kd ;
4) 计算静应力 st ； 5) 计算动应力 d = Kd st .
注意
1) 对于不是垂直冲击或水平冲击问题，或不满 足条件（冲击前无应力和变形），则需要应
a g
)
记： 若忽视自重，则
对线性系统
a
Kd Kd
1 a
g
g
动荷系数
内力、应力、应变和变形都与外力成线性关系。
动载荷问题旳求解 1) 求出动荷系数； 2) 按静载荷求解应力、应变、变形等； 3) 将所得成果乘以动荷系数 Kd 即可。 6
动载荷问题旳求解
1) 求出动荷系数；

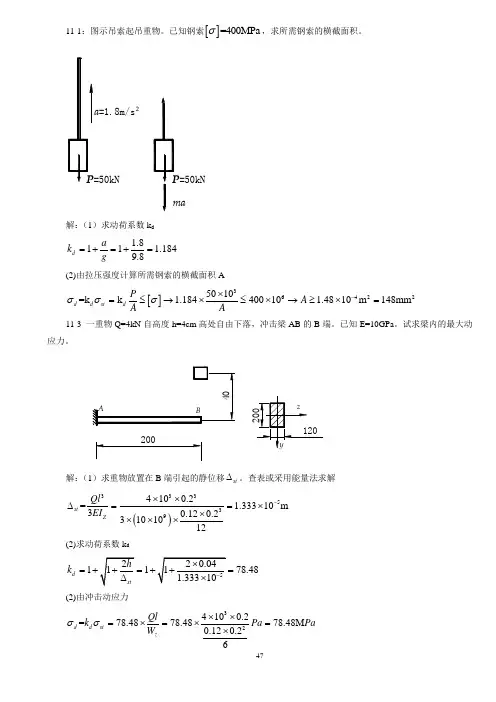
第十一、十二章 动荷载和循环应力

第十一、十二章 动荷载和循环应力

11-1：图示吊索起吊重物。

已知钢索[]=400MPa σ，求所需钢索的横截面积。

2=1.8m/s=50kN解：（1）求动荷系数k d1.811 1.1849.8d a k g =+=+= (2)由拉压强度计算所需钢索的横截面积A[]364225010=k k 1.18440010 1.4810m 148mm d d st d P A A Aσσσ-⨯=≤→⨯≤⨯→≥⨯=11-3 一重物Q=4kN 自高度h=4cm 高处自由下落，冲击梁AB 的B 端。

已知E=10GPa 。

试求梁内的最大动应力。

解：（1）求重物放置在B 端引起的静位移st ∆。

查表或采用能量法求解()3335394100.2= 1.33310m 30.120.23101012st ZQl EI -⨯⨯∆==⨯⨯⨯⨯⨯(2)求动荷系数k d1178.48d k =+=+= (2)由冲击动应力324100.2=78.4878.4878.48M 0.120.26d d st z Ql k Pa Pa W σσ⨯⨯=⨯=⨯=⨯11-4 图示工字钢梁右端置于弹簧上，弹簧常数c=0.8kN/mm,梁的E=200GPa，[]=160MPaσ，重物Q自由下落，求许可下落高度h。

z4433=113010mm=14110mmzzW⨯⨯解：（1）求C截面的静挠度st∆333394-1233-4-3-451021510 =+4822c48200101130101040.810/103.68710+1.56251019.31210mstQl QEI-⨯⨯⨯∆⋅=+⨯⨯⨯⨯⨯⨯⨯=⨯⨯=⨯（）（）（2）求动荷系数d11k=+=+（3）求危险点在静力荷载时的应力339(510)244Pa=17.73MPa1411010z zQlMW Wσ-⨯⨯===⨯⨯max,j（4）由强度条件求冲击时的许可高度[]17.73160=(10.0612m=612mmd dhkσσσ==⨯≤→+≤max，max,j.11-8 重物Q自H高处自由下落到曲拐上，试按第三强度理论写出危险点的相当应力。

材料力学第10章(动载荷)

材料力学第10章(动载荷)
突加荷载 h 0,
Kd 2
二、水平冲击 mg v
d
Fd d ， Pst st
Pst mg 其中： mgl st EA
Fd
st
Pst
mv2 冲击前：动 T1 能 2
冲击后： 应变能Vε 2 Fd d 2
2 F 2 st mv d mg
h
P
h
解：
st
Pl 1.7 102 (mm) EA
2h K d 1 1 st
2 500 1 1 243 2 1.7 10
l
l
d 2 A 4
P 2 103 0.028(MPa) st 4 A 7.1 10 d Kd st
假设： (1)冲击物为刚体； (2)不计冲击过程中的声、光、热等能量损耗（能量守恒）；
(3)冲击过程中被冲击物的变形为线弹性变形过程。(保守计算)
一、自由落体冲击
P
冲击前： T 0
V P(h d )
B
h
A
冲击后：
1 Vε d Fd d 2
A
Δd
能量守恒： T V Vd
B
2h st
l
4 Pl 3 22mm st 3 EI
K d 1 1 2 50 3.35 22
40 C 30
d Kd st
M max Pl 50(MPa) st W W
d Kd st 161 MPa) (
A
Δd
Fd
B
1 P (h d ) Fd d 2 Fd d P st
2 Fd 1 Fd P (h st ) st P 2 P

材料力学动荷载和交变应力(xu)

材料力学动荷载和交变应力(xu)

Mechanics of Materials
FNd ( x)
=
( Axγ
+
P)(1 +
a) g
=
FNst (1 +
a) g
FNd ( x)
σd (x) =
FNd A
=
Axγ + P (1 + a )
A
g
=
σ
st (1 +
a )
g Ax γ
令
Kd
= 1+
a g
----动荷因数
Ax γ
a
xg
则 Fd = Kd FNst σ d = Kdσ st
强度条件: σ d max = k d (σ st )max ≤ [σ ]
[ 材料力学 \
Mechanics of Materials
Kd = 1+
1 + 2h Δ st
$注意：动荷系数中的 Δst为把冲击物作为静荷载置于
被冲击物的冲击点处，被冲击物的冲击点沿 冲击方向的静位移。
$讨论：
1.当h=0时，k d = 2 表明把重物挨着构件,突然松手,
=
1 2
× 201.1×12
= 1 206.6 N
2m
2m
12m
FN
qst
FN
2m
2m
12m
[ 材料力学 \
Mechanics of Materials
FN
qst
2m 12m
2 q st
＋
6 q st
FN 吊索的静应力
2m
σ st
=
FN A
=
1 206.6 108

第十、十一章 动荷载和循环应力解读

钢索
Mechanic of Materials
a
W
例1
§ 10.1 概述
钢索
解：（1）对重物进行受力分析
Mechanic of Materials
惯性力: FI ma （2）沿竖直方向建立
FT a
W
a
W
“平衡方程”： Y 0 FT W FI 0 a FT ma mg (1 )W g （3）求动应力若钢索截面积为A
3、掌握作加速直线运动或匀速转动时的动应力计 算、构件受冲击荷载时的动应力计算。
重点：冲击荷载时的动应力计算 难点：疲劳极限曲线 学时安排：2
第二十七讲目录 第十章 动载荷
§ 10.1 概述 §10.4 杆件受冲击时的应力和变形
Mechanic of Materials
第十一章 交变应力
§ 11.1 交变应力与疲劳失效
Mechanic of Materiaห้องสมุดไป่ตู้s
y
qd ds an
Nn F
惯性力:
qd Ag AgD 2 an w g 2g

平衡方程
j
Nn F
x
2 N qd sin
0
D d 0 2
2 N qd D 0 qd D Ag D 2 2 N w 2 4g
§ 10.1 概述
kd
v g st
2
§10.4 杆件受冲击时的应力和变形 Mechanic of Materials
例题 图中所示的两根受重物Q冲击的钢梁，其中一根是支承于刚性 支座上，另外一根支于弹簧刚度系数k=100N/mm的弹性支座上。 已知l = 3m, h=0.05m, Q=1kN, I=3.4×107mm4, E=200GPa,比较 两者的冲击应力。

材料力学课件11_动荷载与交变应力_浙江大学

1、动应力
基本思想 —— 将动力学问题转化为静力学 问题，建立方程求解。
方法： 基于达朗伯原理的动静法 工程上通过动荷因素描述
例11-1. 杆OA长为L，横截面积为A，重量为P1，弹性模
量为E，A端固结物重为P，杆与物以角速度ω在水平面 内转动。试求杆的最大动应力与伸长。
ω
O
A
解： 动力学问题（静时无水平力）
d,max
FN,m ax A
L 2
2gA (P1 2P)
由 d,max [ ]得
(3) 杆伸长
2gA[ ]
L(P1 2P)
——许可角速度
L
L 0
FN dx EA
1 EA (FAL
1 3
qAL2 )
L2 2
3EAg
(P1
3P)
例11-2. 圆杆直径为d，长AB＝l，质量密度为，于C、D处
(1) 确定等效静力学问题的荷载——惯性力
按质点→微段dx： 质量 dx P1 , 加速度 a x 2
惯性力 P1 2 xdx L g
q
FA x
gL
O
——线性分布
A
物A的惯性力
FA
P g
L 2
P1 2 g
(2) 杆拉伸
轴力
FN
FA
1 2
qA(L
x2 L
)
O端
FN,m ax
L 2
2g
(P1
2P)
最大动应力
max r 1 ——对称循环交变应力
r 1 ——非对称循环交变应力 r 0 ——脉动循环交变应力
(2) 疲劳寿命——交变应力 ( ma下x )疲劳破坏所
经历的应力循环次数N S－N曲线 max

第十一章动荷载优秀课件

Q(hd)12Fdd 动载荷、静载荷下虎克定律都成立
Q Fd
st d
Fd
Q
st
d
得Q(hd)12Q stdd
Q
h Fd
d
Q st
Q(hd)12Fdd
Q Fd
st d
Fd
Q
st
d
得Q(hd)12Q stdd
整理 d 2 得 2std ： 2 hst0 d可解
dst s2t2hst (实际 d st, “”不取
一、冲击问题的假定
1.不计冲击物的变形(刚体）； 2.冲击物与构件（被冲击物）接触后无回弹，
二者合为一个运动系统； 3.被冲击物的质量（惯性）与冲击物相比很小，
可略去不计，冲击应力瞬时传遍整个被冲击物； 4.整个冲击过程中，构件在线弹性范围内； 5.冲击过程中，声、热等能量损耗很小，可略去
不计。（能量守恒）
q d (5)求动应力
d
FNd 2A
A
FNd
d
R2 2
g
qd
2R
qd
A
qd
A R2
g
FNdqd2R2AgR22
FNd (5)求动应力
d
R2 2
g
vR圆环轴线上的点的 度线速
d
v2 g
说明：圆环内的动应力只与γ和v有关，而与横截面面积无关， 要保证旋转圆环的强度，只能限制圆环的转速，增加面积是不起 作用的。
二、自由落体冲击
Q
h
Fd
d
Q
冲击物Q由高h的地方自由落下 h 被冲击物在线弹性范围
d
Fd 冲 击 荷 载
d 动变形
冲击前
重物Q 被冲击杆
动能

材料力学10动载荷

目录
当载荷突然全部加到被冲击物上， 此时T=0
2T Kd 1 1 Q st
2
Q
由此可知,突加载荷的动荷系数是2，这时所引 起的应力和变形都是静荷应力和变形的2倍。 1.若已知冲击物自高度 h 处无初速下落,冲击
物与被冲击物接触时的速度为v
T
Qv 2g
2
h
v 2 2 gh
2
v 2h 2T 1 1 1 1 Kd 1 1 g st st Q st
d
a
目录
b
设冲击物体与弹簧开始接触的瞬时动能为 T 根据机械能守恒定律，冲击物的动能T和势能 V的变化应等于弹簧的变形能 V d,即
动能T
d
T V V d
1 V d Fd d 2
a
V Qd
b
1 T Q d Fd d 2
在线弹性范围内，载荷、变形和应力成正比， 即：
Ebh 4 wB d K d st 1 1 3 2 Ql
4Ql 3 Ebh3
目录
例10-3：图示钢杆的下端有一固定圆盘，盘
上放置弹簧。弹簧在 1kN的静载荷作用下缩
短0.625mm。钢杆直径d=40mm, l =4m，许用 应力[σ]=120MPa, E=200GPa。若有重为 15kN的重物自由落下，求其许可高度h。
Fd d d Q st st
d Fd Q st
a
b
1 2 d V d Q 2 st
c
目录
V Qd
b
T V V d
a
1 2 d V d Q 2 st
c
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Mechanic of Materials
因此，在此条件下，动应力沿杆长作线性分布，如图:
d
F/A
0
L
x
例2
§ 10.1 概述
a m F
（5）构件轴向变形 取构件当中一微段 dx
dx Fd(x)+dFd
Mechanic of Materials
Fd ( x)dx d ( x) d (L) dx d ( x)dx EA E Fd ( x) Fx d ( x) A AL
FT d A (1 a )W a g (1 ) st A g
FI
st 静载荷情况下的钢索中的应力：
例1
§ 10.1 概述
讨论 1：
FT a
Mechanic of Materials
引入：动载荷因数kd
W
a kd 1 g
有:
FI
d k d st
a (1 )W FT a g d (1 ) st A A g
y qd ds an
Nn F
圆截面上的应力为:
N g D2 2 g v 2 d w A 4g g
Mechanic of Materials
j
Nn F
则强度条件可以写为 :
钢索
Mechanic of Ma1
§ 10.1 概述
钢索
解：（1）对重物进行受力分析
Mechanic of Materials
惯性力: FI ma （2）沿竖直方向建立
FT a
W
a
W
“平衡方程”： Y 0 FT W FI 0 a FT ma mg (1 )W g （3）求动应力若钢索截面积为A
Mechanic of Materials
§ 10.1 概述 交变载荷（交变载荷引起疲劳破坏） Mechanic of Materials
§ 10.1 概述
一、构件作等速直线运动时的动应力与动变形
Mechanic of Materials
1、此类问题的特点:
加速度保持不变或加速度数值保持不变，即角速度w =0 2、解决此类问题的方法: 牛顿第二定律 动静法（达朗伯原理）
§ 10.1 概述
3、达朗伯原理的回顾 用静力学的方法求解动力学的问题。 虚拟的“惯性力”
Mechanic of Materials
FI ma
惯性力与主动力、约束力共同构成“平衡力 系”，通过静力学平衡方程求解未知力。
§ 10.1 概述 例1： 起重机以等加速度 a 起吊重量为 W的物体，求钢索中的应力。
3、动应力、动变形 构件由于动荷载所引起的应力、变形 4、分类：惯性载荷、冲击载荷、振动载荷、交变载荷
5、研究意义
§ 10.1 概述
二、实例 惯性载荷
Mechanic of Materials
§ 10.1 概述
冲击载荷
Mechanic of Materials
§ 10.1 概述
振动载荷（Tacoma大桥共振断裂）
§ 10.1 概述
4、动应力、动变形与动载荷因数的关系
Mechanic of Materials
动应力:
d k d st
d k d st
[ ] st kd
在线弹性范围内，动变形亦有: 强度条件:
d k d st [ ]
§ 10.1 概述
例 2： 设有等直杆，长度为L，截面积为A，比
Mechanic of Materials
y
qd ds an
Nn F
惯性力:
qd Ag AgD 2 an w g 2g

平衡方程
j
Nn F
x
2 N qd sin
0
D d 0 2
2 N qd D 0 qd D Ag D 2 2 N w 2 4g
§ 10.1 概述
§ 11.2 交变应力的循环特征、应力幅和平均应力
§ 11.3 持久极限 § 11.4 影响持久极限的因素
§ 10.1 概述
一、什么是动载荷，与静荷载的区别。
Mechanic of Materials
1、静荷载： 从零开始缓慢地增到终值，然后保持不变的载荷 2、动载荷：
使构件产生明显的加速度的载荷或随时间变化 的载荷。动载荷本质：是惯性力
Mechanic of Materials
重g，受拉力F的作用，以等加速度a运动，求构件 的应力和变形。（不计摩擦力）
a m F
例2
§ 10.1 概述
a m F
解：（1）构件加速度:
a F F Fg m ALg / g ALg
Mechanic of Materials
（2）构件单位长度上的惯性力(集度):
第二十七讲的内容、要求、重难点 教学内容：
Mechanic of Materials
构件作加速直线运动或匀速转动时的动应力计算， 构件受冲击荷载时的动应力计算；交变应力的概念， 交变应力下材料的疲劳破坏，疲劳极限。
教学要求：
1、了解材料疲劳极限曲线、提高疲劳强度措施；
2、理解动荷载和循环应力概念，循环应力的类型；
qd
gA 1
g
a
F L
（3）用截面法取构件的一部分加以分析各截面的轴力:
x qd Fd(x)
X 0
Fd ( x) qd x 0
F Fd ( x) x L
例2
§ 10.1 概述
d ( x)
Fd ( x) Fx x st A AL L
a m F
（4）动应力为: 静载荷条件下的应力-静应力: st
3、掌握作加速直线运动或匀速转动时的动应力计 算、构件受冲击荷载时的动应力计算。
重点：冲击荷载时的动应力计算 难点：疲劳极限曲线 学时安排：2
第二十七讲目录 第十章 动载荷
§ 10.1 概述 §10.4 杆件受冲击时的应力和变形
Mechanic of Materials
第十一章 交变应力
§ 11.1 交变应力与疲劳失效
L
l 0
Fd(x)
Fx FL dx EAL 2 EA
§ 10.1 概述 二、构件作等速转动时的动应力 设圆环以等角速度w 绕通过圆心且垂直 于圆环平面的轴旋转，如图所示（平均直 径D>>厚度t，讨论环内的应力。 Mechanic of Materials
w
D
§ 10.1 概述
二、构件作等速转动时的动应力 环内任意一点有向心加速度an，设圆环的横截 面积为A，单位体积的重量为g。