应力应变关系

应力应变关系及材料力学性能研究引言：应力应变关系是材料力学性能研究的基础，关乎着材料在外力作用下的变形与破坏。

本文将探讨应力应变关系的基本概念，并分析其对材料力学性能的影响。

一、应力与应变的定义：应力是指材料在外力作用下受到的内部力，为单位面积上的力。

常见的应力类型有拉应力、压应力、剪应力等。

应变是材料在受力作用下发生的变形程度，为单位长度上的变化量。

常见的应变类型有线性应变、剪应变等。

二、线弹性材料的应力应变关系：对于线弹性材料而言，应力应变关系可以通过胡克定律来描述。

胡克定律表明应力与应变之间呈线性关系，且比例系数为弹性模量。

应力=弹性模量 ×应变这意味着线弹性材料在弹性区内总是遵循胡克定律，即应力的增加与相应的应变呈线性关系。

三、非线性材料的应力应变关系：然而，并非所有材料都遵循胡克定律。

在超出线弹性范围的情况下，材料可能表现出非线性应力应变关系。

例如，在塑性变形时，材料产生塑性畸变，应力与应变之间的关系失去了线性性。

此时，材料的应力应变关系可由应力应变曲线来描述。

四、应力应变关系对材料强度和韧度的影响：应力应变关系直接决定了材料的力学性能，其中强度和韧度是两个重要的指标。

强度是指材料在外力作用下承受的最大应力，可以通过应力应变曲线中的极限强度来衡量。

强度高的材料能够承受更大的外力，具有较好的抗压能力。

韧度是指材料在断裂前能够吸收的能量，可以通过应力应变曲线下的面积来衡量。

韧度高的材料具有较好的抗拉伸能力和耐冲击性。

应力应变关系的形状和斜率都会对材料的强度和韧度产生影响。

通过调整材料的成分、结构和加工方式，可以改变应力应变关系，从而改善材料的力学性能。

五、应力应变关系的实验测定：测量材料的应力应变关系是材料力学性能研究的重要手段。

常见的实验方法包括拉伸试验、压缩试验和剪切试验等。

在实验中，使用应变计和力传感器等设备来测量应变和应力的变化。

通过绘制应力应变曲线，可以获取材料的弹性模量、屈服强度、极限强度、延伸率等参数。

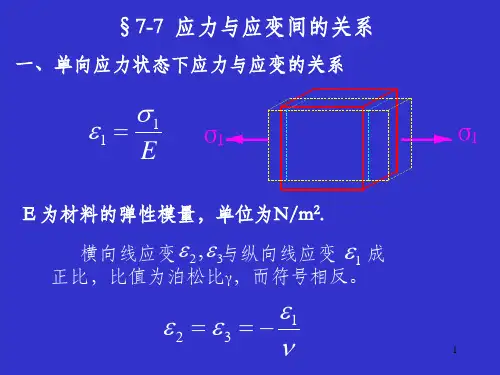
弹性体力学中的应变与应力关系弹性体力学是研究物体在力的作用下变形和恢复原状的力学分支学科，研究的对象主要是固体物质。

在弹性体力学中，应变与应力是两个重要的概念，它们描述了物体的变形和受力状态。

应变和应力之间的关系在弹性体力学中具有重要意义，它们可以通过材料力学模型来描述。

应变是物体在受力作用下发生形变的程度。

一般来说，我们可以将应变分为线性应变和非线性应变。

线性应变是指物体的形变与受力成正比。

例如，当我们拉伸一根弹簧时，弹簧的长度会发生变化，而这种形变与拉力之间是线性相关的。

用数学的语言来表达，线性应变可以用应变量ε表示，其与外力F之间存在着关系ε=ΔL/L，其中ΔL为物体长度的增量，L为物体的原始长度。

非线性应变则是指物体的形变与受力不成比例。

在高强度材料的情况下，非线性应变是不可忽视的。

非线性应变与材料的本构关系有关，常用的本构关系模型包括背应变率本构关系、黏弹性本构关系等。

这些模型可以更准确地描述材料的力学行为，使得我们能够更准确地计算应变。

与应变相对应的是应力。

应力可以看作是物体单位面积的受力情况。

一般来说，应力可以分为正应力和剪应力。

正应力是指垂直于物体内部某一面的力的作用情况。

例如，当我们用一把剪刀剪断一根木棍时，剪刀的受力情况可以被描述为正应力。

剪应力则是指平行于物体内部某一面的力的作用情况。

例如，当我们剪断一个绳索时，绳索的受力情况可以被描述为剪应力。

应变与应力之间的关系又可以通过应力-应变曲线来描述。

应力-应变曲线是弹性体力学研究中的一个重要工具，它可以体现材料的力学性质。

一般来说，应力-应变曲线可以分为弹性阶段、屈服阶段、塑性阶段和断裂阶段。

在弹性阶段，应力与应变成正比。

这个阶段的曲线是一个直线，斜率即为弹性模量，用来描述材料的刚度。

当应力超过一定值时，物体进入屈服阶段。

在屈服阶段，物体的应变不再与应力成正比，而是呈现出非线性关系。

此时物体会发生塑性变形，形成剩余应变。

当应力进一步增加时，物体可能发生断裂。

我所认识的应力应变关系应力应变都是物体受到外界载荷产生的响应。

物体由于受到外界载荷后，在物体内部各部分之间要产生互相之间的力的作用，由于受到力的作用就会产生相应的变形;或者由于变形引起相应的力的作用。

则一定材料的物体其产生的应力和应变也必然存在一定的关系。

一 应力－应变关系影响本构关系的因素有很多,例如材料、环境、加载类型（载荷、温度)、加载速度(动载荷、静载荷）等,当然，本构关系有很多类型，包括弹性、塑性、粘弹性、粘塑性、各向同性、各向异性本构关系,那么首先来叙述一下简单情况本构关系，所谓简单情况就是六个应力分量x y xy yz zx σσστττ、、z 、、、只有一个不为零,六个应变分量x y xy yz zx εεεγγγ、、z 、、、只有一个自由变化，应力应变关系图1－1。

图1-1 应力应变关系图图中O Ａ为线弹性阶段，AB 为非线弹性阶段，故ＯB 为初始弹性阶段，C 点位初始屈服点,()s σ+为初始屈服应力，CBA 为弹性阶段卸载,这一阶段中E σε=,初始弹性阶段结束之后，应力继续增大,进入塑性阶段,CDE 为强化阶段，应变强化硬化,EF 为颈缩阶段，应变弱化软化。

如果在进入塑性阶段卸载后再加载，例如在D 点卸载至零,应力应变关系自D 点沿'DO 到达'O 点,且'DO ∥O Ａ，其中'O O 为塑性应变p ε，ＤG 为弹性应变e ε，总应变为它们之和。

此后再继续加载，应力应变关系沿ODE Ｆ变化,D 点为后继屈服点,ＯD 为后继弹性阶段，()'s σ+为后继屈服应力，值得一提的是初始屈服点只有一个,而后继屈服点有无数个（由加载历史决定）。

若在卸除全部载荷后反向加载,弹性阶段'COC ,()()s s σσ+-=,而在强化阶段'DOD ，()()s s σσ+->,称为Bau ｓchin ｇｅr 效应。

从上述分析得出材料弹塑性行为有一定的特殊性,主要表现在:弹性应力应变关系是线性，且是单值对应关系，而塑性应力应变关系是非线性的非单值对应。

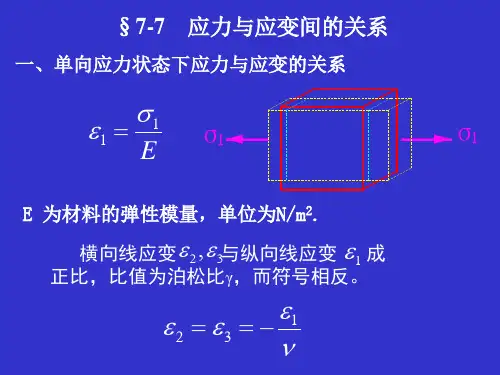
4 应力应变关系4.1弹性变形时应力和应变的关系当材料所受应力小于其线弹性极限时，材料应力应变间的关系服从广义Hooke 定律，即1()1()1()111222x x y z y yx zz z x yxy xy yz yz zx zxE E E G G G εσνσνσεσνσνσεσνσνσετετετ⎧=--⎪⎪⎪=--⎪⎨⎪=--⎪⎪⎪===⎩，， （4.1） 式中，E 为拉压弹性模量，G 为剪切模量，ν为泊松比，对于各向同性材料，三个常数之间满足()21E G ν=+关系。

由上式可得11212()()33m x y z x y z m E E ννεεεεσσσσ--=++=++= （4.2） 于是11()'2x m x m x E G νεεσσσ+-=-= 或1112''22x m x x m G G Eνεεσσσ-=+=+ 类似地可以得到1112''22y m y y m G G E νεεσσσ-=+=+ 1112''22z m z z m G G Eνεεσσσ-=+=+于是，方程（4.1）可写成如下形式1212'00'0000'x xy xz x xy xz m v yx y yz yx y yz m G E m zx zy z zx zy z εγγσττσγεγτστσσγγεττσ-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭即'1122ij ij m ij ij m G Eνεεεσδσ-'=+=+ （4.3）显然，弹性变形包括体积改变的变形和形状改变的变形。

前者与球应力分量成正比，即12m m E νεσ-= （4.4）后者与偏差应力分量成正比，即''12''12''12111222x x m x G y y m y G z z m z G xy xy yz yz zx zxG G G εεεσεεεσεεεσετετετ⎧=-=⎪=-=⎪⎨=-=⎪⎪===⎩，，或简写为2ij ij G σε''= （4.5）此即为广义Hooke 定律。

应力-应变
应力-应变关系是材料力学中的重要概念，用于描述材料在受到外力作用下的变形行为。

应力（stress）指单位面积上的力，通常用力（force）除以面积（area）来计算。

应变（strain）则指材料单位长度的变化量，通常用长度变化（change in length）除以初始长度（original length）来计算。

应力和应变之间的关系可以通过材料的应力-应变曲线表示。

在弹性阶段，应力与应变成正比，即呈线性关系，这称为胡克定律。

当超过弹性极限后，材料可能发生塑性变形，应力-应变曲线非线性上升。

最终，在断裂点达到时，材料会发生破坏。

值得注意的是，不同材料具有不同的应力-应变特性，因此需要使用适当的试验方法来确定每种材料的特定应力-应变曲线。

这些实验通常在材料力学测试机上进行，例如拉伸试验、压缩试验或剪切试验等。

总而言之，应力-应变关系是描述材料变形行为的重要概念，可以通过应力-应变曲线来了解材料的力学特性。

流体力学中应力应变关系流体力学是力学的一个分支，研究的是流体的运动、应力和应变。

在流体力学中，应力和应变之间的关系是一个基础性问题，本文将对流体力学中应力应变关系进行讲解。

一、应力和应变的概念应力是指在物体内部的任意一个点处，单位面积受到的力的大小。

在流体力学中，应力分为正应力和剪应力两种。

正应力是指垂直于物体表面的应力，它的方向和大小与物体表面的法线方向相同。

剪应力是指平行于物体表面的应力，它的方向和大小与物体表面的切线方向相同。

应变是指物体受到应力作用后，形态发生改变的程度。

在流体力学中，应变分为体积应变和剪应变两种。

体积应变是指流体的体积在受到压力作用后发生的变化，它是指流体体积的变化与初始体积的比值。

剪应变是指物体受到剪应力作用后，产生的形变的强度，它是指变形的尺寸与原始尺寸的比值。

流体在受到应力作用时，会发生形变，而应力和应变之间的关系便是描述形变程度的应变和导致形变的应力之间的关系。

在流体力学中，应力和应变之间的关系有两种：1. 线性应力应变关系在一些情况下，流体的应变与应力之间具有线性关系。

这种关系表示为：ε = K σ其中，ε是流体的应变，K是常数，σ是流体的应力。

这种关系在流体受到小应力时是适用的，通常称为胡克定律。

当流体所受到的应力超过一定的范围时，线性应力应变关系不再成立，流体的应变不再是应力的线性函数。

这时，应力和应变的关系可以用更复杂的非线性关系进行描述。

液滴的表面张力、黏度和压缩强度是非线性的。

流变学是研究物质的变形和流动行为的学科，它探究物体在不同的应力作用下，应变的变化规律。

在流体力学的领域中，流体的应力应变关系可以被分成三类：粘弹性流体是一种介于固体和液体之间的物质，它的应变不仅与应力有关，而且与应变历史有关。

它们的应力应变关系可以用弹性模量、黏度和时间来描述。

塑性流体是指流体在受到一定应力作用后会发生永久变形的流体。

在塑性流体中，应变随着应力的增大，在一定的应力范围内也是线性的，但超过一定的范围后便不再线性。