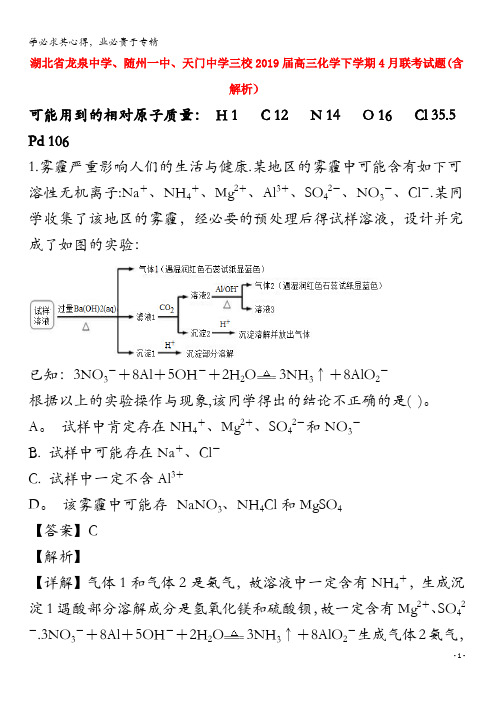
湖北省2019年龙泉中学、随州一中、天门中学三校高三四月联考理科数学

湖北天门2019高三下联考（一）-数学(理）数学试卷〔理〕【一】选择题〔本大题共10小题，每小5分，共50分，在每题给出的四个选项中，只有一项为哪一项符合题目要求的〕 1、复数z 1=2＋i ，z 2=3＋2i ，那么21z z z =在复平面内所对应的点是 A 、(81,55)B 、81(,)55- C 、81(,)55--D 、81(,)55- 2、假设5()ax x+的展开式中3x 的系数为10，那么实数a 的值是A.3B.2C.1-D. 123、函数2()21log f x x x =-+的零点所在区间是A 、〔18，14〕B 、〔14，12〕C 、〔12，1〕D 、〔1，2〕①“2,0x x x ∀∈->R ”的否定是“2,0x x x ∃∈->R ”； ②假设|21|1x ->，那么101x <<或10x<； ③5,21x x *∀∈+N 是奇数、 A 、0 B 、1C 、2D 、35、直线l α⊥平面，直线m β⊂平面，有下面四个命题： ①α∥β,l m ⇒⊥②l αβ⊥⇒∥,m ③l ∥,m αβ⇒⊥， ④l m ⊥⇒α∥β.其中正确的两个命题是 A 、①与②B 、①与③ C 、②与④ D 、③与④6、如图给出的是计算111124620++++的值的一个 程序框图，其中判断框内应填入的内容是 A 、i ＞20 ？ B 、i ＜20 ？C 、i ＜10？ D 、i ＞10？7、函数2()sin cos f x x x x =+-A、2(,3πB、5(,6πC、2(3π-D 、(,0)3π8、函数2|log |1()2x f x x x =--，那么不等式1()2f x f ⎛⎫< ⎪⎝⎭的解集等于 A 、(14，12)∪(3，+∞) B 、(14，3) C 、(0，12)∪(2，+∞)D 、(12，2)9、双曲线2222:1(0,0)x y C a b a b-=>>的半焦距为c ，过焦点且斜率为1的直线与双曲线C 的左右两支各有一个交点，假设抛物线24y cx =的准线被双曲线C2〔e 为双曲线C 的离心率〕，那么e 的值为 ABC 、32或3D10、方程(1)(||2)4y x ++=，假设对任意[,](,)x a b a b ∈∈Z ，都存在[0,1]y ∈使方程成立，且任意[0,1]y ∈，都有[,](,)x a b a b ∈∈Z 使方程成立，那么a b +的最大值等于A 、0B 、2C 、4D 、6【二】填空题〔本大题共5小题，每题5分，共25分，把答案填在答题卷中相应的横线上〕 11、某中学开学后从高一年级的学生中随机抽取80名学生进行家庭情况调查，通过一段时间后再从那个年级随机抽取100名学生进行学情调查，发明有20名同学上次被抽到过，可能那个学校高一年级的学生人数为、12、某几何体的三视图如下图，那么它的体积是、13、S n 是数列{}n a 的前n 项和，向量(1,2)n a =--a ，(4,)n S =b 满足⊥a b ，那么53S S =、14、假设自然数n 使得作加法(1)(2)n n n ++++运算均不产生进位现象，那么称n 为“理想数”、例如32是“理想数”，因32+33+34不产生进位现象；23不是“理想数”，因23+24+25产生进位现象、设小于1000的所有“理想数”的各个数位上的数字组成集合A ， 那么用集合A 中的数字可组成无重复数字的三位偶数的个数为、 15〔1〕、如图，圆O 的直径AB ＝8，C 为圆周上一点，BC ＝4，过点C 作圆的切线l ，过点A 作直线l 的垂线AD ，D 为垂足，AD 与圆O 交于点E ，那么线段AE 的长为、〔2〕、在平面直角坐标系下，曲线122:x t a C y t =+⎧⎨=-⎩〔t 为参数〕，，曲线22sin :12cos x C y θθ=⎧⎨=+⎩〔θ为参数〕，假设曲线C 1、C 2有公共点，那么实数a 的取值范围为、【三】解答题〔本大题共6个小题，共75分，解承诺写出文字说明，证明过程或演算步骤〕16、〔本小题总分值12分〕函数2()2sin(0)2xf x x ωωω->的最小正周期为3π、〔Ⅰ〕求函数()f x 的表达式；〔Ⅱ〕在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对的边，且a b c <<2sin c A =，求角C 的大小； 〔Ⅲ〕在〔Ⅱ〕的条件下，假设311()2213f A π+=，求cos B 的值、17、〔本小题总分值12分〕实验小学三年级的英语老师要求学生从星期一到星期四每天学习3个英语单词；每周五对一周内所学单词随机抽取假设干个进行检测〔一周所学的单词每个被抽到的可能性相同〕 〔Ⅰ〕英语老师随机抽了4个单词进行检测，求至少有3个是后两天学习过的单词的概率； 〔Ⅱ〕某学生对后两天所学过的单词每个能默写对的概率为45，对前两天所学过的单词每个能默写对的概率为35、假设老师从后三天所学单词中各抽取一个进行检测，求该学生能默写对的单词的个数ξ的分布列和期望、18、〔本小题总分值12分〕如图，在四棱锥ABCD -PGFE 中，底面ABCD 是直角梯形，侧棱垂直于底面，AB //DC ，∠ABC＝45o ，DC ＝1，AB ＝2，PA ＝1、 〔Ⅰ〕求PD 与BC 所成角的大小； 〔Ⅱ〕求证：BC ⊥平面PAC ； 〔Ⅲ〕求二面角A -PC -D 的大小、 19、〔本小题总分值12分〕 函数2()ln ,f x x ax x a =+-∈R 、〔Ⅰ〕假设0a =，求曲线()y f x =在点〔1，(1)f 〕处的切线方程； 〔Ⅱ〕假设函数()f x 在[1，2]上是减函数，求实数a 的取值范围；〔Ⅲ〕令2()()g x f x x =-，是否存在实数a ，当(0,]x e ∈〔e 是自然对数的底数〕时，函数()g x 的最小值是3？假设存在，求出a 的值；假设不存在，说明理由、20、〔本小题总分值13分〕 如图，椭圆2222:1(0)x y E a b a b +=>>，E 的左顶点为A 、上顶点为B ，点P 在椭圆上，且△PF 1F 2的周长为4+〔Ⅰ〕求椭圆的方程；〔Ⅱ〕设C 、D 是椭圆E 上两不同点，CD //AB ，直线CD与x 轴，y 轴分别交于M 、N 两点，且存在实数,λμ 使得MC CN λ=，MD DN μ=，求λμ+的取值范围、21、〔本小题总分值14分〕函数()f x 的图象通过点〔1，λ〕，且对任意x ∈R ，都有(1)()2f x f x +=+、数列{}n a 满足12a λ=-，12,(),nn n n a f a n +⎧⎪=⎨⎪⎩ 〔Ⅰ〕求()()f n n *∈N 的表达式； 〔Ⅱ〕设3λ=，求1232n a a a a ++++；〔Ⅲ〕假设对任意n *∈N ，总有112n n n n a a a a +++<，求实数λ的取值范围、2018届天门市高三联考(一)参考答案【一】选择题〔每题5分，共40分〕 1、A 【解析】32(32)(2)88125555i i i i z i i ++-+====++对应的点〔81,55〕在第一象限,应选A 、2、B 【解析】略3、C 【解析】因为211()log 1022f ==-<，2(1)1log 110f =+=>，因此()f x 的零点在 〔12，1〕内，应选C 、4、C 【解析】①错，应是2,0x x x ∃∈-≤R 、②正确，由|21|1x ->，得211x -<-或211x ->，为奇数 为偶数即0x <或1x >，因此101x <<或10x<、③正确，5,2x x *∀∈N 是偶数，4,21x x *∀∈+N 是奇数，应选C 、5、B 【解析】略6、D 【解析】111124620S =++++为10个偶数之和，因此判断框内应填入i ＞10，应选D 、7、B 【解析】化简得：()sin(2)3f x x π=+，应选B 、8、D 【解析】当1x ≥时，2|log |111()2()x f x x x x x x x =--=-+=，111()2(2)222f =+-=， 因此由()f x <1()2f 得112x >，解得12x ≤<、当01x <<时，2|l o g|111()2()x f x x x x xxx =--=+-=，因此由()f x <1()2f 得102x <<、综上得选C 、 9、B 【解析】由题意，得2222b a =，即2b =，因此222429c a a e -=， 即422990e e -+=，22(23)(3)0e e --=，因此23e =或232e =，又因为1b a >，因此2e >，因此23e =，应选B 、 10、B 【解析】先画出函数41||2y x +=+的图象，由题意和图象可得20,22,02(,)a b a b a b -≤≤==-≤≤∈Z 或，因此a b +的最大值为0+2=2，应选B 、【二】填空题〔每题5分，共30分〕 11、400【解析】2080805400100÷=⨯=，故填400、 12、2250【解析】几何体为一个长方体截去一个三棱柱，因此体积为15×10×2012-×15×5×20=2250，故填2250、13、317【解析】由41)20n n =(a S --=a b ，得22n n S a =-、当1n =时，由11122a S a ==-，得12a =；当2n ≥时，由1122(22)n n n n n a S S a a --=-=---，得12n n a a -=，因此2n n a =，从面55332(12)2(12)S S -==-317、故填317、14、10【解析】由题意，得A ={0，1，2，3}，个位数是0的三位偶数有236A =个；个位数是2的三位偶数有2224A =个，共有10个、故填10、15、〔1〕【解析】连接AC ，那么AC ⊥BC 、由条件得AC =∠DCA ＝60o，因此DC =，6DA =、由切割线定理，得2DC DE DA =，因此1226DE ==， 因此624AE =-=、故填4、〔2〕[1，1【解析】化为一般方程，得1:220C x y a +-=，222:(1)4C x y +-=、2≤，即1a -≤11a ≤≤+[1，1+]、【三】解答题〔共80分〕 16、〔Ⅰ〕1cos ()22sin()126x f x x x ωπωω-=-=+-………………………………2分 函数()f x 的最小正周期为3π，即23ππω=，解得23ω=、∴2()2sin()136f x x π=+-……3分2sin c A =∴sin sin a A c C ==……………5分又sin 0A ≠，∴sin C =…………6分又a b c <<，∴23C π=……7分 〔Ⅲ〕由311()2213f A π+=，得12cos 13A =………………9分 ∵03A π<<，∴5sin 13A =………………………………11分∴cos cos()cos cos sin sin 333B A A A πππ=-=+……………12分17、〔Ⅰ〕设英语老师抽到的4个单词中，至少含有3个后两天学过的事件为A ，那么由题意可得314666412C C +C 3()C 11P A ==…………………………………………………5分 〔Ⅱ〕由题意可得ξ可取0，1，2，3，那么有P (ξ=0)2122()55125=⨯=………6分P (ξ=1)1224121319C ()55555125=⨯⨯⨯+⨯=，P (ξ=2)2124241356()+C 55555125=⨯⨯⨯⨯=，…………………………………9分 P (ξ=3)24348()55125=⨯=…………………………………………………10分 因此ξ的分布列为：…11分故E ξ=0×2125+1×19125+2×56125+3×48125=115……………………………12分18、〔Ⅰ〕取的AB 中点H ，连接DH ，易证BH//CD ，且BD =CD …………………1分因此四边形BHDC 为平行四边形，因此BC//DH因此∠PDH 为PD 与BC 所成角………………………………………………2分 因为四边形，ABCD 为直角梯形，且∠ABC =45o ，因此⊥DA ⊥AB又因为AB =2DC =2，因此AD =1，因为Rt △PAD 、Rt △DAH 、Rt △PAH 都为等腰直角三角形，因此PD =DH =PH，故∠PDH =60o………………………4分〔Ⅰ〕连接CH ，那么四边形ADCH 为矩形，∴AH =DC 又AB =2，∴BH =1 在Rt △BHC 中，∠ABC =45o，∴CH =BH =1，CB∴AD =CH =1，AC∴AC 2+BC 2=AB 2∴BC ⊥AC ……6分又PA 平面ABCD ∴PA ⊥BC ……7分∵PA ∩AC =A ∴BC ⊥平面PAC ………………………………………8分〔Ⅲ〕如图，分别以AD 、AB 、AP 为x 轴，y 轴，z 轴建立空间直角坐标系，那么由题设可知：A (0，0，0)，P (0，0，1)，C (1，1，0)，D (1，0，0)， ∴AP =(0，0，1)，PC =(1，1，-1)…………………………………………9分设m =(a ，b ，c )为平面PAC 的一个法向量，那么00AP PC ⎧=⎪⎨=⎪⎩m m ，即00c a b c =⎧⎨+-=⎩设1a =，那么1b =-，∴m =(1，-1，0)………………………………………10分 同理设n =(x ，y ，z )为平面PCD 的一个法向量，求得n =(1，1，1)………11分∴1cos ,2===m n m n m n因此二面角A -PC -D 为60o…………………………………………………12分19、〔Ⅰ〕当0a =时，2()ln f x x x =-…………………………………………………1分 因此1()2f x x x'=-，(1)1f '=…………………………………………………2分又(1)1f =，因此曲线()y f x =在点〔1，(1)f 〕处的切线方程为0x y -=……………3分〔Ⅱ〕因为函数在[1,2]上是减函数， 因此2121()20x ax f x x a x x+-'=+-=≤在[1,2]上恒成立、……………4分 令2()21h x x ax =+-,有(1)0(2)0h h ≤⎧⎨≤⎩，得172a a ≤-⎧⎪⎨≤-⎪⎩…………………………5分故72a ≤-………………………………………………………………………6分〔Ⅲ〕假设存在实数a ，使()ln ((0,])g x ax x x e =-∈有最小值3，11()ax g x a x x-'=-=①0a ≤时，()0g x '<，因此()g x 在(0,]e 上单调递减，min ()()13g x g e ae ==-=，4a e=〔舍去〕②当1ea≥时，()0g x '<在(0,]e 上恒成立，因此()g x 在(0,]e 上单调递减，min ()()13g x g e ae ==-=4a e=〔舍去〕……………………………9分③当10e a <<时，令()0g x '<，得10x a<<，因此()g x 在1(0,)a 上单调递减，在1(,]e a上单调递增因此min1()()1ln 3g x g a a==+=，2a e =，满足条件…………………11分 综上，存在实数2a e =，使得x ∈(0,]e 时，()g x 有最小值3、………12分 20、〔Ⅰ〕由题意得224a c c e a ⎧+=+⎪⎨==⎪⎩2分解得24a =，23c =，从而21b =， 因此椭圆的方程为2214x y +=……………………………………………4分〔Ⅱ〕因为A 〔-2，0〕，B 〔0，1〕，因此12ABk =…………………………………5分由CD//AB ，可设直线CD 的方程为12y x m=+〔1m ≠±〕………………6分 由得(2,0)M m -，(0,)N m设11(,)C x y ，22(,)D x y 由221412x y y x m ⎧+=⎪⎪⎨⎪=+⎪⎩得222220x mx m ++-=……………………………………………………7分 由22(2)4(22)0m m =-->，得22m <…………………………………8分因此，122x x m +=-，21222x x m =-……………………………………9分由MC CN λ=得1111(2,)(,)x m y x m y λ+=--因此112x m x λ+=-，即121m x λ=--，同理，由MD DN μ=，得221m x μ=--……………………………………11分因此1212121122()22x x m m x x x x λμ++=--+=--⨯=22222211m m m -+=--………………………………………………12分 由22m <⇒221m -(,2](2,)∈-∞-⋃+∞ 因此λμ+(,2](2,)∈-∞-⋃+∞………………………………………………13分 21、〔Ⅰ〕记()nb f n =，由(1)()2f x f x +=+，有12n n bb +-=对任意n *∈N 都成立……………………………………………1分又1(1)b f λ==，因此数列{n b }为首项为λ，公差为2的等差数列………2分故n b =22n λ+-…………………………………………………………………3分即()22f n n λ=+-………………………………………………………………4分〔Ⅱ〕由题设3λ=，假设n 为偶数，那么12n n a -=………………………………………………………5分假设n 为奇数，且3n ≥，那么21111()222222221n n n n n n a f a a λλλ-----==+-=+-=+-=+ (7)分又121a λ=-=故111,121,2,n n n n a n n--=⎧⎪=+⎨⎪⎩a 1+a 2+a 3+…+a 2n =(a 1+a 3+…+a 2n -1)+(a 2+a 4+…+a 2n )=(20+22+…+22n －2+n -1)(21+23+…+22n －1)……………………………………9分 =(1+21+22+…+22n －1)+n -1=22n +n -2……………………………………10分〔Ⅲ〕当n =1时，显然成立，当n 为奇数且n ≥3时，a n +1a n +2-a n a n +1=a n +1(a n +2-a n )=2n [2n +12λ+--(2n -12)λ+-]=3×22n －10>…11分当n 为偶数时，a n +1a n +2-a n a n +1=a n +1(a n +2-a n )=(2n 2)λ+-(2n +1-2n －1)=3×2n －1(2n 2)λ+-………………………………………………………………12分为奇数且n ≥3为偶数∵a n a n +1<a n +1a n +2，∴2n 2λ+-0>…………………………………………13分 ∵n 为偶数，∴n ≥2∵2n 2λ+-单调递增，∴420λ+->∴2λ>- 故λ的取值范围为〔-2，+∞〕………………………………………………14分。

2019届下学期湖北省重点高中联考协作体高三4月月考试卷理科数学注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷一、选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写．．．．．在答题卷上．．．．．） 1．在复平面内，复数满足，则的共轭复数对应的点位于（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．已知集合，集合，则（ ）A ．B ．C ．D ．3．根据如下样本数据：得到回归方程，则（ ） A ．变量与之间是函数关系 B ．变量与线性正相关 C ．线性回归直线经过上述各样本点D ．4．《张丘建算经》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有女不善织，日减功迟，初日织五尺，末日织一尺，今三十织迄，问织几何．”其意思为：有个女子不善于织布，每天比前一天少织同样多的布，第一天织五尺，最后一天织一尺，A ．30尺 B ．150尺 C ．90尺 D ．180尺5．已知实数满足，则目标函数的最大值等于（ ）A ．-14B ．-5C ．4D ．66．已知直线，平面，且，，下列命题：①； ②③；④其中正确的序号是（ ） A ．①②B ．①③C ．②④D ．③④7．运行如图所示的程序框图，若输出是126，则①应为（ ）A ．B ．C ．D ．8．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为（ ）A ．B ．C ．D ．9．若双曲线的中心为原点，是双曲线的焦点，过直线与双曲线交于两点，且的中点为，则双曲线的方程为（ ）z (1)2z i -=z {12}M x x =-<{(1)(3)0}N x Z x x =∈+-≤M N ={0,1,2}{1,0,1,2}-{1,0,2,3}-{0,1,2,3}^1.412.4yx =-+x y x y 5a =,x y 11021x y x x y -≤⎧⎪+≥⎨⎪+≤⎩42Zx y =+,l m ,αβl α⊥m β⊂//l m αβ⇒⊥//l m αβ⊥⇒//l m αβ⇒⊥//l m αβ⊥⇒S 7?n ≤5?n <5?n ≤6?n ≤112π163π173π356π(2,0)F -F l ,M N (1,3)P 此卷只装订不密封班级 姓名 准考证号考场号 座位号A ．B ．C ．D ． 10．已知函数（）的图象与直线的某两个交点的横坐标分别为，若的最小值为，且将函数的图象向右平移个单位得到的函数为奇函数，则函数的一个递增区间为（ ） A ． B ． C ．D ．11．已知点是抛物线的焦点，点为抛物线的对称轴与其准线的交点，过作抛物线的切线，切点为，若点恰在以为焦点的双曲线上，则双曲线的离心离为（ ） A ．BC ．D12．已知函数是上的奇函数，当时，，则函数在上的所有零点之和为（ ） A ．0B ．4C ．8D ．16第Ⅱ卷二、填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上．．．．．．．．．．） 13．在中，，，则 ． 14．已知，的展开式中项的系数为1，则的值为 ． 15．已知各项都为正数的数列，对任意的，恒成立，且，则 ．16．若以曲线上任意一点为切点作切线，曲线上总存在异于的点，以点为切点作线，且，则称曲线具有“可平行性”，下列①；②；③；④三、解答题（本题共6个小题，共70分．解答应写出必要的文字说明、证明过程或演．．．．．．．．．．．．．．．．．．．算步骤，请把答案写在答题卷上．．．．．．．．．．．．．．） 17．（12分）在中，设内角的对边分别为，且．（1）求角；（2）若且，求的面积．18．（12分）从某校高中男生中随机选取100名学生，将他们的体重（单位：）数据绘制成频率分布直方图，如图所示：2213x y -=2213x y -=2213y x -=2213y x-=()2sin()f x x ωϕ=+0ϕπ<<2y =12,x x 21x x -π()f x 4π()f x (,0)2π-(,)44ππ-(0,)2π3(,)44ππ1F 24x y =2F 2F A A 12,F F 2121()f x R 0x >112,02()1(2),22x x f x f x x --⎧<≤⎪=⎨->⎪⎩()()1g x xf x =-[7,)-+∞ABC ∆AB AC AB AC -=+3AB =AB BC ∙=0a >4(1)(2)ax x ++2x a {}n a *,m n N ∈m n m n a a a +∙=35472a a a ∙+=212227log log log a a a +++=()y f x =(,)M x y l M 11(,)N x y N 1l 1//l l ()y f x =1y x=3y x x =-cos y x =2(2)ln y x x =-+ABC ∆,,A B C ,,a b c sin()sin()442C C ππ-++=C c =sin 2sin A B +ABC ∆kg（1）估计该校的100名同学的平均体重（同一组数据以该组区间的中点值作代表）； （2）若要从体重在，内的两组男生中，用分层抽样的方法选取5人，再从这5人中随机抽取3人，记体重在内的人数为，求其分布列和数学期望．19．（12分）等边的边长为3，点分别为上的点，且满足（如图1），将沿折起到的位置，使二面角成直二面角， 连接，（如图2） （1）求证：平面；（2）在线段上是否存在点，使直线与平面所成的角为？若存在， 求出的长；若不存在，请说明理由．20．（12分）在平面直角坐标系中，点，圆， 点是圆上一动点，线段的中垂线与线段交于点． （1）求动点的轨迹的方程；（2）若直线与曲线相交于两点，且存在点（其中不共线），使得被轴平分，证明：直线过定点．[60,70)[70,80)[60,70)ξ()E ξABC ∆,E F ,AB BC 12AD CE DB EA ==ADE ∆DE 1A DE ∆1A DE B --1A B 1A C 1A D ⊥BCED BC P 1PA 1A BD 060PBxOy 1(F222:130F x y +--=Q 1F Q 2F Q P P E l E ,A B (4,0)D ,,A B D ADB ∠x l21．（12分）已知函数．（1）若，函数的极大值为，求实数的值；（2）若对任意的，，在上恒成立，求实数的取值范围．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．做答时，用2B 铅笔在答题卡上把所选题目对应的题号涂黑． 22．（10分）【选修4-4：坐标系与参数方程】已知曲线的参数方程为，其中为参数，且在直角坐标系中，以坐标原点为极点，以轴正半轴为极轴建立极坐标系． （1）求曲线的极坐标方程；（2）设是曲线上的一点，直线被曲线点的极坐标．23．（10分）【选修4-5：不等式选讲】 已知函数，（1）求，的取值范围；（2）若，对，都有不等式恒成立，求的取值范围．2()()x f x ax x a e -=++()a R ∈0a ≥()f x 5ea 0a ≤()ln(1)f xb x ≤+[0,)x ∈+∞b C cos 1sin x y αα=+⎧⎨=⎩α[0,]απ∈xOy O x C T C OT C T ()f x x x a =-a R ∈(1)(1)1f f +->a 0a >,(,]x y a ∀∈-∞5()4f x y y a ≤++-a2019届下学期湖北省重点高中联考协作体高三4月月考试卷理 科 数 学 答 案一、选择题． 1-5：DADCC6-10：BDBDA 11-12：BC二、填空题． 13．9-14．15．21 16．①③三、简答题． 17．【答案】（1）；（2）．【解析】（1），故由已知可得：，即， 又．（2）由及正弦定理得， 由（1），又，故由余弦定理得，解得，从而，． 18．【答案】（1）；（2）分布列见解析，．【解析】（1）依频率分布直方图得各组的频率依次为， 故估计100名学生的平均体重约为：61π3C =ABC S =△ )4cos(42sin )4sin(C C C +=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-=-ππππ22)4sin()4cos(=+++C C ππ21cos 22)2sin(2=∴=+C C π30ππ=∴<<C C B A sin 2sin =b a 2=3π=C 33=c 3cos )2(2)2()33(222πb b b b -+=3=b 6=a 239233621sin 21=⨯⨯⨯==∴∆C ab S ABC 64.5() 1.8E ξ=10.0,20.0,30.0,35.0,05.0．（2）由（1）及已知可得：体重在的男生分别为：， ，从中用分层抽样的方法选5人，则体重在内的应选3人，体重在内的应选2人，从而的可能取值为1，2，3，且得，， ，其分布列为：故得． 19．【答案】（1）证明见解析；（2）存在满足条件的点P ，且PB 的长为． 【解析】（1）证明：如图1，由已知可得：， 从而， 故得，， 即图2中：，为二面角的平面角，而二面角为直二面角，，即，，．（2）由（1）两两垂直，分别以建立5.6410.08520.07530.06535.05505.045=⨯+⨯+⨯+⨯+⨯[)[)807070,60，及0.30100=30⨯（人）0.20100=20⨯（人）[)60,70[)70,80ξ()10313513===C C P ξ()532352312===C C C P ξ()10133533===C C P ξ8.110135321031)(=⨯+⨯+⨯=ξE 2560,1,2===A AD AE 360cos 2122122=⨯⨯⨯-+= DE 222AE DE AD =+DE BD DE AD ⊥⊥∴,DE BD DE D A ⊥⊥,1DB A 1∠∴B DE A --1B DE A --1 901=∠∴DB A DB D A ⊥1BCED ,平面且⊂=DB DE D DB DE BCED D A 平面⊥∴1DE DB DA ,,1轴所在直线为z y x DA DE DB ,,,,1空间直角坐标系，则由已知及（1）可得， 令，则因， 故， 即，由（1）知为平面的一个法向量， 又， 若存在满足条件的P ，则， 即， 解得，而，故存在满足条件的点P ，且PB 的长为． 20．【答案】（1）；（2）证明见解析．【解析】（1）由已知，，圆的半径为， 依题意有：，，故点P 的轨迹是以为焦点，长轴长为4的椭圆，即，故点P 的轨迹E 的方程为．（2）令，因A ，B ，D 不共线，故的斜率不为0，)0,233,21(),1,0,0(),0,0,2(),0,0,0(1C A B D )10(≤≤=→→λλBC BP )0,0,2(),0,233,23(=-=→→DB BC )0,233,232()0,233,23()0,0,2(λλλλ-=-+=+=+=→→→→→BC DB BP DB DP )0,233,232(λλ-P )0,1,0(=→n BD A 1)1,233,232(1--=→λλAP 2360sin ,cos 1==→→ P A n 23)1()233()232(233222=-++-λλλ65=λ25,3==∴=→→→BC BP BC λ251422=+y x )0,3(1-F )0,3(2F 2F 4=r PQ PF =142221===+=+∴r QF PF PQ PF PF 21,F F 1,2,3=∴==b a c 1422=+y x ),(),,(2211y x B y x A l可令的方程为，则由，得， 则，① 被轴平分，， 即，亦即② 而， 代入②得③①代入③得， 时得：此时的方程为：过定点（1，0）， 时，亦满足此时的方程为：，综上所述，直线恒过定点（1，0）． 21．【答案】（1）；（2）． 【解析】（1）由题意，．①当时，， 令，得；，得，所以在单调递增单调递减． 所以的极大值为，不合题意． ②当时，，令，得；，得或，l n my x +=2244x my n x y =+⎧⎨+=⎩042)4(222=-+++n mny y m 44,422221221+-=⋅+-=+m n y y m mn y y ADB ∠ x 0=+∴DB DA k k 0442211=-+-x y x y 0)(4211221=+-+y y x y x y )(2)()(212112211221y y n y my n my y n my y x y x y ++=+++=+0))(4(22121=+-+y y n y my m 2)44(22+-m n 0)42)(4(2=+--+m mn n 0≠m 1=n l 1+=my x 0=m 1=n l 1=x l 2=a 1b ≥)(x f )1,(-∞),1(+∞)(x f ee f 51)1(≠=所以在单调递增，，单调递减．所以的极大值为，得． 综上所述． （2）令，，当时，，故上递增，， 原问题上恒成立，①当时，，，，此时，不合题意．②当时，令，，则，其中，，令，则在区间上单调递增， （ⅰ）时，，所以对，，从而在上单调递增，所以对任意，， 即不等式在上恒成立． （ⅱ）时，由，及在区间上单调递增， 所以存在唯一的使得，且时，．从而时，，所以在区间上单调递减，)(x f )1,11(a -)11,(a --∞),1(+∞)(x f ee af 512)1(=+=2=a 2=a (]0-)(，于∞a g )0(,)0()(≥=≤∴-x xe g a g x ∴[)+∞∈+≤⇔-,0)1ln(x x b xe x 于)(x p [)+∞,0则时，，即，不符合题意．综上所述． 22．【答案】（1）；（2）． 【解析】（1）根据曲线的参数方程得曲线C 的普通方程为， 曲线的极坐标方程为．（2）由题得，，则解得． 故点的极坐标为． 23．【答案】（1）；（2）． 【解析】（1）由得或或，， 综上所述，． （2）当时，记， 则， 即， 当，， 2cos (0,)2πρθθ⎡⎤=∈⎢⎥⎣⎦)6πC 22（x-1）1y +=C 2cos (0,)2πρθθ⎡⎤=∈⎢⎥⎣⎦3=OT 2cos θ=0,2πθ⎡⎤∈⎢⎥⎣⎦6πθ=(3,)6π)21,(--∞∈a (]0,5a ∈R a a x x x f ∈-=,)(1111)1()1(>+--⇔>-+a a f f {11)1()1(-<>++-⇔a a a {111)1()1(≤≤->+--a a a {11)1()1(>>+--a a a φ∈-<≤--<⇔a a a 或或211121-<⇔a )21,(--∞∈a (])0(,>∞-∈a a y a y y y g -++=45)()45(,454545)(=≤≤-+=+≥-++=时取a y a a y a y y g a y g +45)(的最小值为(])0(,>∞-∈a a x 4)2()()(22a a x x a x x f +--=-=时的最大值为， 故原问题， 又，∴．2a x =∴)(x f 42a 5105445422≤≤-⇔≤--⇔+≤⇔a a a a a 0a >(]0,5a ∈。

2019年龙泉中学、随州一中、天门中学三校高三4月联考理科综合能力测试注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔在答题卡上填写自己的准考证号、姓名、试室号和座位号。

用2B型铅笔把答题卡上试室号、座位号对应的信息点涂黑。

2．选择题每小题选出答案后，用2B型铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡整洁。

考试结束后，将试卷和答题卡一并交回。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 Cl 35.5 Pd 106一、选择题：本题共13小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．关于细胞代谢的叙述，正确的是A．外界溶液浓度大于细胞液浓度时，即使细胞没有发生质壁分离，也不能判断是死细胞B．细胞内能量通过ATP分子在吸能反应和放能反应之间循环流通C．在剧烈运动过程中，肌细胞释放CO2量/吸收O2量的值将增大D．无氧呼吸能产生ATP，但没有[H]的生成过程2．二倍体植物(AaBb)用秋水仙素处理后获得四倍体植物。

下列关于该二倍体植物有丝分裂后期细胞和该四倍体植物减数第一次分裂后期细胞的叙述，正确的是A．两者的基因型相同，移向细胞两极的基因可能不同B．两者的染色体数目相同，染色体的形态结构不同C．两者的DNA分子数目相同，但前者无染色单体D．两者的染色体行为变化相同3．某种植物的叶色与花色皆是由一对等位基因控制，研究人员任取红叶植株与绿叶植株杂交，F1均表现淡红叶;任取红花植株与白花植株杂交，F1均表现淡红花。

研究人员经分析认为叶色和花色是由同一对基因控制的，若让淡红叶淡红花植株自交，则下列关于子代的预期不能支持该看法的是A．红叶植株皆开红花B．绿叶植株皆开白花C．淡红叶淡红花植株占1/4 D．红叶红花植株占1/4 4．下列有关人体内环境稳态和生命活动的调节的说法，正确的是A．稳态是机体在神经系统的调节下，通过各个器官、系统的协调活动来共同维持的B．兴奋传导时，突触前膜释放的神经递质通过胞吐进入下一个神经元发挥作用C．免疫系统由免疫器官、淋巴细胞、免疫活性物质组成D．人体饥饿时，血液流经肝脏后，血糖的含量升高；血液流经胰岛后，血糖的含量减少5．假设某种群的起始数量为N0，N t表示t年后种群的数量，如图表示N t/N0值随着时间变化的曲线。

湖北天门2019高三下联考（二）-数学(理）数学试卷〔理〕【一】选择题〔本大题共10小题，每题5分，共50分.在每题列出的四个选项中,选出最符合题目要求的一项〕 1、集合A ＝{0，2}，B ＝{-1，0，a ＋3}，且A B ⊆，那么a 等于 A 、1B 、0C 、-1D 、-32、i 是虚数单位，那么复数23z i 2i 3i =++所对应的点是 A 、〔2，2〕B 、〔-2，2〕C 、〔-2，-2〕D 、〔2，-2〕3、在△ABC 中，“0>AB BC ”是“△ABC 为钝角三角形”的A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分又不必要条件4、设随机变量ξ服从正态分布(3,4)N ，假设(23)(2)P a P a ξξ<-=>+ 那么a 的值为 A 、5B 、3C 、73D 、535、六棱锥P -ABCDEF 的底面是正六边形，PA ⊥平面ABC 、那么以下结论正确的个数是 ①CD //平面PAF ②DF ⊥平面PAF ③CF //平面PAB ④CF //平面PAD A 、1B 、2试C 、3D 、46、双曲线222212x y b -=的渐近线与圆22(2)1x y +-=相切，那么双曲线的焦距为A 、8B 、4C 、2D 、1 7、0t >，假设(21)6t x dx -=⎰，那么t 的值等于A 、2B 、3C 、6D 、88、函数sin()(0)y x πϕϕ=+>的部分图象如下图，设P 是图象的最高点，A 、B 是图象与x 轴的交点，那么tan APB ∠＝ A 、10B 、8C 、87D 、479、数列{}n a 的通项公式为|13|n an =-，那么满足119102k k k a a a +++++=的整数kA 、有0个B 、有1个C 、有2个D 、有3个10、设点A 〔1，0〕，B 〔2，1〕，假如直线1ax by +=与线段AB 有一个公共点，那么22a b +A 、最小值为15BC 、最大值为15D【二】填空题〔本大题共5小题，每题5分，共25分.其中15题为选做题〕 11、在△ABC 中，假设B ＝2A ，a ：b ＝1，那么A ＝、 12、在521x x ⎛⎫+ ⎪⎝⎭的展开式中，x 2的系数是、13、定义某种运算⊗，a ⊗b 的运算原理如下图、 设()(0)(2)f x x x x =⊗-⊗、那么(2)f ＝、 14、数列{}n a 满足11a =，11n nn a a n λ+-=+，其中λ∈R ，n =1，2…、〔1〕当0λ=时，20a ＝、〔2〕假设存在正整数m ，当n ＞m 时，0n a <恒成立，那么λ的取值范围是、15、〔1〕如图，AB 是圆O 的直径，P 在AB 的延长线上，PD 切圆O 于 点C 、圆OOP ＝2，那么PC ＝，∠ACD 的大小为、 〔2〕在极坐标系中，点A2,2π⎛⎫⎪⎝⎭关于直线:cos 1l ρθ=的对称点的一个极坐标为、【三】解答题〔本大题共6小题，共75分、解承诺写出必要的文字说明、证明过程或演算步骤〕16、〔本小题总分值12分〕函数cos2()sin()4x f x x π=+的定义域为D ，集合A=[,]ππ-、〔Ⅰ〕求D A ；〔Ⅱ〕假设4()3f x =，求sin 2x 的值、 17、〔本小题总分值12分〕如图，菱形ABCD 的边长为6，∠BAD ＝60o ，AC ∩BD ＝O 、将菱形ABCD 沿对角线AC 折起，使BD ＝B -ACD 、〔Ⅰ〕假设点M 是棱BC 的中点，求证：OM //平面ABD ； 〔Ⅱ〕求二面角A -BD -O 的余弦值；〔Ⅲ〕设点N 是线段BD 上一个动点，试确定点N 的位置，使得CN＝结论、18、〔本小题总分值12分〕甲班有2名男乒乓球选手和3名女乒乓球选手，乙班有3名男乒乓球选手和1名女乒乓球选手，学校计划从甲、乙两班各选2名选手参加体育交流活动、 〔Ⅰ〕求选出的4名选手均为男选手的概率；〔Ⅱ〕记X 为选出的4名选手中女选手的人数，求X 的分布列和期望、 19、〔本小题总分值12分〕 函数()(1)(0)xa f x e x x=->，其中e 为自然对数的底数、 〔Ⅰ〕当a ＝2时，求曲线()y f x =在〔1，(1)f 〕处的切线与坐标轴围成的面积； 〔Ⅱ〕假设函数()f x 存在一个极大值点和一个极小值点，且极大值与极小值的积为e 5，求a 的值、 20、〔本小题总分值13分〕椭圆2222:1(0)x y M a b a b +=>>的离心率为3，且椭圆上一点与椭圆的两个焦点构成的三角形周长为6+〔Ⅰ〕求椭圆M 的方程；〔Ⅱ〕设直线l 与椭圆M 交于A 、B 两点，且以AB 为直径的圆过椭圆的右顶点C ，求△ABC 面积的最大值、21、〔本小题总分值14分〕函数()()ln 1f x x ax =+-的图象在1x =处的切线与直线210x y +-=平行、〔Ⅰ〕求实数a 的值； 〔Ⅱ〕假设方程()()134f x m x =-在[]2,4上有两个不相等的实数根，求实数m 的取值范围；〔Ⅲ〕设常数1p ≥，数列{}n a 满足()1ln n n n a a p a +=+-〔n ∈+N 〕，1ln a p =、求证：1n na a +≥、2018年天门卷2参考答案【一】选择题〔每题5分，共50分〕1、C 【解析】因为A B ⊆，因此2B ∈，从而32,1a a +==-，应选C 、2、C 【解析】232312322z i i i i i =++=--=--对应的点是〔-2，-2〕，应选C 、3、A 【解析】由于0AB BC >，得0BA BC <，从而B 为钝角，反之，△ABC 为钝角三角形，可能是A 或C 为钝角，应选A 、 4、C 【解析】(3,4),(23)(2)N P a P a ξξξ<-=>+，23a 2a ∴-+与关于3μ=对称.23232.a a -++∴=，解得73a ∴=，应选C 、5、C 【解析】由CD//AF 知A 正确，由DF ⊥AF 知B 正确，由CF//BA 知C 正确，应选C 、6、A 【解析】由直线0bx ay ±=与圆22(2)1x y +-=1=，得22224a a b c =+=,因此28c =，应选A 、7、B 【解析】由2200(21)()|6tt x dx x x t t -=-=-=⎰，且0t >，解得2t =，应选B 、8、B 【解析】过P 点作PC ⊥x 轴C ，那么由条件得22AB πω==，11,2PC AC ==，因此1322tan tan()813122APB APC BPC +∠=∠+∠==-⨯，应选B 、 9、C 【解析】因为102不是10的倍数，因此13k <，因此由119102k k k a a a +++++=，得(13)(12)101(6)k k k -+-+++++++(13)(14)(6)(7)22k k k k --++=+27112102k k =-+=，即27100k k -+=，解得2k =或5k =，应选C 、10、A 【解析】线段AB 的方程为1(12)y x x =-≤≤，与1ax by +=联立，解得1b x a b+=+、因此由112b a b +≤≤+，得0121a b a a b +>⎧⎪≤⎨⎪+≥⎩或0121a b a a b +<⎧⎪≥⎨⎪+≤⎩可行域如下图，显然22a b +无最大值，22a b +的最小值即为原点到直线21a b +=的距离的平方，即为215=，应选A 、【二】填空题〔每题5分，共25分〕 11、30o【解析】因为sin sin sin sin sin 22sin cos a A A A b B A A A====，因此cos A =，又0o＜A ＜180o ，因此A ＝30o ，故填30o 、 12、5531015521C C rr rr r r T x xx --+⎛⎫== ⎪⎝⎭、令3102r -=，得4r =、因此2x 的系数是45C 5=，故填5、13、-2【解析】(2)(02)2(22)0222f =⊗⨯-⊗=⨯-=-、故填-2说明：另外此题能够增加求()f x 在区间[－2，2]上的最小值，那么： 当20x -≤≤时，2()f x x x x x x =-=-+取最小值－6、当02x <≤时，()0f x x x x =-=-取最小值－2、因此()f x 在区间[－2，2]上的最小值为-6、14、120；(21,2),k k k *-∈N 【解析】〔1〕0λ=时，11n n n a a n +=+，11n n a n a n +=+， 因此201922019181191817111201918220a aa a a a a ===、 〔2〕1231(2)(1)1,,,223a a a λλλ---===⨯4(3)(2)(1),4!a λλλ---=(1)(2)(1)!n n n a n λλλ-----=、要使0n a <，需负因数的个数为奇数个，当212k k λ-<<，如今存在2(*)m k k N ≥∈,当n m >时，0n a <恒成立。

【校级联考】湖北省龙泉中学、随州一中、天门中学三校2019届高三四月联考理科数学试题学校_________ 班级__________ 姓名__________ 学号__________一、单选题1. 已知复数z在复平面上对应的点的坐标为（-1,1）,则( )A．z-1是实数B．z-1是纯虚数C．z-是实数D．z+是纯虚数2. 设A，B，U是三个集合，且“”是“”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件3. 知，则的大小为（）A．B．C．D．4. 命题“若则且”的否定是（）A．若B．若C．若D．若5. 如图，角为始边，终边与单位圆O分别交于点A，B，则（）A．B．C．D．6. 在正方形网格中，某四面体的三视图如图所示，如果小正方形网格的边长为1，那么该四面体的体积为（）C．D．A．B．7. 我国南宋时期的数学家秦九韶（约1202-1261）在他的著作（数书九章）中提出了多项式求值的秦九韶算法.如图所示的框图给出了利用秦九韶算法求多项式的一个实例.若输入的，，，则程序框图计算的结果为（）A．15 B．31 C．63 D．1278. 某公司为了解用户对其产品的满意度，从甲、乙两地区分别随机调查了100个用户，根据用户对产品的满意度评分，分别得到甲地区和乙地区用户满意度评分的频率分布直方图．若甲地区和乙地区用户满意度评分的中位数分别为m1，m2；平均数分别为s1，s，则下面正确的是（）2A．m1＞m2，s1＞s2B．m1＞m2，s1＜s2C．m1＜m2，s1＜s2D．m1＜m2，s1＞s29. 如图所示，正方形上连接着等腰直角三角形，等腰直角三角形腰上再连接正方形，…，如此继续下去得到一个树形图形，称为“勾股树”.若某勾股树含有255个正方形，且其最大的正方形的边长为，则其最小正方形的边长为（）A．B．C．D．10. 在直角坐标系中,对于点,定义变换:将点变换为点,使得其中.这样变换就将坐标系内的曲线变换为坐标系内的曲线.则四个函数,,,在坐标系内的图象,变换为坐标系内的四条曲线（如图）依次是A．②,③,①,④B．③,②,④,①C．②,③,④,①D．③,②,①,④11. 已知直线与，并且公共点的横、纵坐标均为整数，则这样的直线共有（）条.A．60 B．66 C．72 D．78二、填空题12. 若展开式的二项式系数之和为8，则展开式中含项的系数为_______.13. 已知函数的部分图象如图所示，则函数图象的对称中心为__________ .14. 若任取实数对，则“”的概率为________.15. 在底面是菱形的四棱锥P-ABCD中，∠点E为线段PD上一点，且，则点P到平面ACE的距离为_________.三、解答题16. 已知△ABC的内角A，B，C的对边长分别为a，b，c，且（1）求角A的大小；（2）若a=2，求△ABC的面积的最大值.17. 如图，在四棱锥P-ABCD中，已知且四边形ABCD为直角梯形，分别为PA，PD的中点.（1）求证：∥平面；（2）点Q是线段BP上的动点，当直线CQ与DM所成角最小时，求线段BQ的长.18. 在信息时代的今天，随着手机的发展，“微信”成为人们交流的一种主要方式，某机构通过网络平台对“使用微信交流”的态度进行调查，有数万人参与（全部参与者年龄均在[15，65]之间），现从参与者中随机选出200人，经统计这200人中使用微信交流的占.将这些使用微信交流的人按年龄分组：第1组[15，25)，第2组[25，35)，第3组[35，45)，第4组[45，55)，第5组[55，65]，得到的频率分布直方图如图所示.（1）从第1，2，3组中用分层抽样的方法抽取12人，再从这12人中随机抽取3人参加网络春晚活动，求至少有1人年龄在[35，45)的概率；（2）把年龄在第1，2，3组的人称为青少年组，年龄在第4，5组的人称为中老年组，若选出的200人中不使用微信交流的的中老年人有26人，问是否有99%的把握认为“使用微信交流”与年龄有关？附：0.15 0.10 0.05 0.025 0.010 0.005 0.0012.072 2.7063.841 5.024 6.635 7.879 10.828参考公式：19. 如图，已知椭圆焦距为2，F为椭圆C的右焦点，A（－a,0），（1）求椭圆C的方程；（2）设O为原点，P为椭圆C上一点，AP的中点为M，直线OM与直线交于点D，过O且平行于AP的直线与直线求证：20. 已知函数（1）求函数的极值.（2）当时，证明21. 在平面直角坐标系中，直线的倾斜角为，且过点M（0，1）.以原点O为极点，轴非负半轴为极轴且取相同的单位长度建立极坐标系，曲线C的极坐标方程为（1）求直线的参数方程（设为参数）与曲线C的直角坐标方程；（2）若直线经过点（1，0），且与曲线C相交于A，B两点，求的值.22. 已知函数（1）当时，求不等式的解集；（2）若不等式的解集为，求实数的取值范围.。

2019年龙泉中学、随州一中、天门中学三校高三4月联考理科综合物理试题二、选择题：本题共8小题，每小题6分，共48分。

在每小题给出的四个选项中，第14～17题只有一项符合题目要求，第18～21题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分。

1.甲、乙两物体同时从同一地点出发，其速度-时间图象如图所示。

下列说法正确的是A. 第1s末两物体相遇B. 前2s内两物体的平均速度相同C. 甲、乙两物体运动的加速度相同D. 甲的位移不断减小，乙的位移不断增大【答案】B【解析】【详解】A．由图象与时轴所围的面积表示位移可知，甲的位移比乙的位移更大，故A错误；B．由图象可知，前2s内两物体的位移相同，所以前2s两物体的平均速度相同，故B正确；C．图象的斜率表示加速度，由图象可知，两物体的加速度方向相反，故C错误；D．由图象与时轴所围的面积表示位移可知，甲、乙两物体的位移都增大，故D错误。

2.用轻弹簧连接的A、B两小球质量分别为m和M(m<M)，静止在光滑水平面上。

若使A球获得瞬时速度v(如图甲)，弹簧压缩到最短时的长度为L1；若使B球获得瞬时速度v(如图乙)，弹簧压缩到最短时的长度为L2，则L1与L2的大小关系为A. L1>L2B. L1<L2C. L1=L2D. 不能确定【答案】C【解析】 【分析】当弹簧压缩到最短时，两球的速度相同，A 、B 两球组成的系统动量守恒，根据动量守恒定律和能量守恒定律结合判断；【详解】当弹簧压缩到最短时，两球的速度相同，对甲图取A 的初速度方向为正方向，由动量守恒定律得：由机械能守恒定律得：。

联立解得弹簧压缩到最短时有：同理：对乙图取B 的初速度方向为正方向，当弹簧压缩到最短时有：故弹性势能相等，则有：，故ABD 错误，C 正确。

【点睛】本题考查动量守恒定律及机械能守恒定律，要注意明确能量的转化情况，并掌握动量守恒的条件。

3.如图甲所示，x 轴上固定两个点电荷Q 1、Q 2（Q 2位于坐标原点O ），其上有M 、N 、P 三点，间距MN =NP 。