几何组成分析

几何组成分析的体会与收获几何学作为一个基础学科，在我们的日常生活和科学研究中都有着重要的地位。

在几何学中，对于图形的组成、结构以及空间中物体的位置和关系有着深刻的研究，而几何组成分析就是一种极其重要的思维方式和方法。

在我的学习和实践中，我深刻感受到了几何组成分析的体会与收获。

一、领会几何组成分析的重要性几何组成分析是几何学中最为重要的分析方法之一，它通过将图形的形态分解成基本的几何元素，从而更好地理解和刻画复杂的物体和空间结构。

因此，几何组成分析在工程技术、艺术、建筑设计等方面都有着广泛的应用。

在我的设计课程中，我曾经遇到过如何设计一个高层建筑的难题。

通过几何组成分析，我将建筑的形态分解成几何元素，再将它们组合起来，设计出了一个兼具美观和实用的建筑。

这一设计的成功，深刻体现了几何组成分析思维的重要性。

二、感受几何组成分析的启示力几何组成分析的思想不仅仅停留在几何学领域，它还可以指导我们在生活中更好地观察和理解事物的本质。

几何组成分析常常被使用于科学研究中，例如通过观察自然界中的几何形态来深入掌握自然的本质规律。

通过运用几何组成分析的思维方式，我们可以更好地理解自然、社会和文化的复杂性，为我们解决实际问题提供有力的启示。

三、探讨几何组成分析的应用前景随着计算机技术的发展，几何组成分析技术得到了极大的应用和发展。

利用计算机几何学和三维数字化技术，可以将几何组成分析应用于制造、计算机辅助设计、数字化娱乐等领域，进一步提高实现精度和效率。

同时，几何组成分析技术将在机器人、人工智能、虚拟现实等领域得到广泛应用和发展。

可以预计，在未来几乎所有的科学和工程技术中，几何组成分析都将起到举足轻重的作用。

四、总结几何组成分析的体会与收获几何组成分析是一种极其重要的思维方式和方法，在我们的日常生活、科学研究和工程技术中都有广泛的应用。

通过几何组成分析的思维方式，我们可以更好地理解并刻画复杂的物体和空间结构，从而更好地解决实际问题。

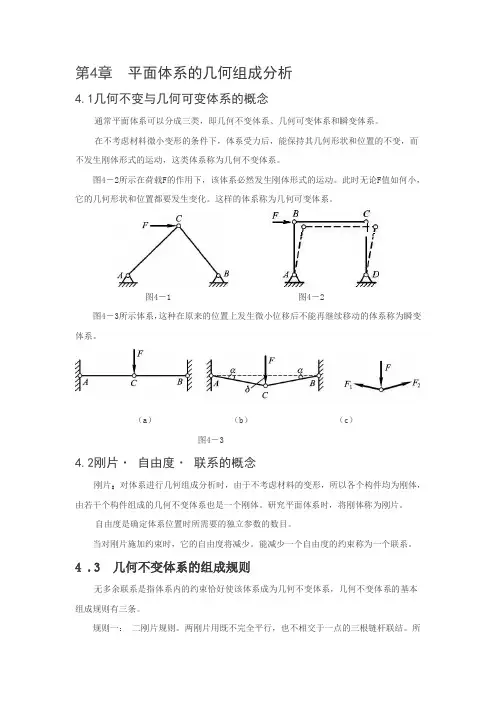
第4章平面体系的几何组成分析4.1几何不变与几何可变体系的概念通常平面体系可以分成三类，即几何不变体系、几何可变体系和瞬变体系。

在不考虑材料微小变形的条件下，体系受力后，能保持其几何形状和位置的不变，而不发生刚体形式的运动，这类体系称为几何不变体系。

图4－2所示在荷载F的作用下，该体系必然发生刚体形式的运动。

此时无论F值如何小，它的几何形状和位置都要发生变化。

这样的体系称为几何可变体系。

图4－1 图4－2图4－3所示体系，这种在原来的位置上发生微小位移后不能再继续移动的体系称为瞬变体系。

（a）（b）（c）图4－34.2刚片·自由度·联系的概念刚片：对体系进行几何组成分析时，由于不考虑材料的变形，所以各个构件均为刚体，由若干个构件组成的几何不变体系也是一个刚体。

研究平面体系时，将刚体称为刚片。

自由度是确定体系位置时所需要的独立参数的数目。

当对刚片施加约束时，它的自由度将减少。

能减少一个自由度的约束称为一个联系。

4 .3 几何不变体系的组成规则无多余联系是指体系内的约束恰好使该体系成为几何不变体系，几何不变体系的基本组成规则有三条。

规则一：二刚片规则。

两刚片用既不完全平行，也不相交于一点的三根链杆联结。

所组成的体系是几何不变的。

规则二：三刚片规则。

三个刚片用不在一条直线的铰两两相联结组成的体系是几何不变的。

规则三：二杆结点规则。

在刚片上加或减去二杆结点时，形成的体系是几何不变的。

4 .4 静定结构和超静定结构·常见的结构形式4.4.1静定结构和超静定结构几何不变体系可分为无多余联系和有多余联系两类。

无多余联系的几何不变体系称为静定结构，有多余联系的几何不变体系则称为超静定结构。

4.4.2常见的结构形式1.梁板体系2.桁架体系3.拱结构体系4.框架、筒体体系5.悬索体系6.薄壳体系7. 膜结构8.树状结构小结(1)体系可以分为几何不变体系和几何可变体系，只有几何不变体系才能用作结构，几何可变及瞬变体系不能用作结构。

几何组成分析的几个概念1、几何不变体系与几何可变体系几何不变体系是指受到任意荷载作用下，若不考虑材料的应变，其几何形状和位置均能保持不变的体系。

几何可变体系是指即使不考虑材料的应变，在微小的荷载作用下也会产生刚体位移，而不能保持原有的几何形状和位置。

几何可变体系分为几何常变体系和几何瞬变体系。

几何可变体系在很小的荷载作用下会产生刚体位移，经微小位移后仍能继续发生刚体运动，这样的几何可变体系称为几何常变体系。

若原为几何可变体系，经微小位移后即转化为几何不变体系，这类几何可变体系称为几何瞬变体系。

工程结构绝不能采用几何瞬变体系，而且也应避免采用接近于瞬变的体系。

2、自由度指体系在所受限制的许可条件下独立的运动方式，即能确定体系几何位置的彼此独立的几何坐标数目。

平面内一点的自由度为2，一个刚片的自由度为3。

3、约束（联系）约束是指限制体系运动的各种装置，包括外部约束（支座约束）和内部约束。

（1）外部约束一个活动铰支座、固定铰支座和固定支座分别相当于1、2、3个约束。

（2）内部约束一根单链杆相当于1个约束；连接j（j>2）个结点的复链杆，相当于2j-3个单链杆，即相当于2j-3个约束；一个单铰相当于2个约束；连接m（m>2）个刚片的复铰，可折合成（m-1）个单铰，即相当于2(m-1)个约束作用；一单刚结点相当于3个约束；连接m（m>2）个刚片的刚结点称为复刚结点，可折合成（m-1）个单刚结点，即相当于3(m-1)个约束。

约束从能否减少体系的自由度方面来考虑，可分为必要约束和多余约束。

为保持体系几何不变所必须具有的约束称为必要约束，不能使体系的自由度数目减少的约束称为多余约束。

4、瞬铰（虚铰）两个刚片间用两个不共线链杆相连，其约束作用相当于这两根链杆交点位置处的一个铰所起的约束作用，这个铰称为虚铰或瞬铰（图1a）。

在几何组成分析中，尤其要注意：两刚片间用两根相互平行的链杆相连，两平行链杆所起的约束作用相当于无穷远处的瞬铰所起的约束作用，如图1b所示。

几何组成分析几何组成分析（也称为结构几何学）是结构力学的一个重要方法，用于研究结构的形态、几何特性及其对结构力学特性的影响。

通过对结构的几何分析，可以获得结构的稳定性、刚度、位移、变形等重要信息，对结构的设计和优化具有重要意义。

几何组成分析的基本原理是根据结构的形态及其载荷情况，利用几何学的基本概念和计算方法，对结构的各个组成部分进行几何分析，并结合材料力学原理，求解结构的刚度矩阵、位移向量和变形矩阵等重要参数。

其中，结构的刚度矩阵描述结构在载荷作用下的刚度特性；位移向量表示结构在载荷作用下的位移；而变形矩阵则描述结构在载荷作用下的变化情况。

1.结构的坐标系及基本概念：建立合适的坐标系，确定结构的基本要素，如结构的节点、杆件或面坯等。

2.结构的构件模型：根据结构的具体形态和几何特性，采用适当的模型对结构的构件进行建模和描述。

3.结构的几何约束：根据结构的形态和几何特性，确定结构的几何约束条件，如节点和杆件的位移、角度等。

4.结构的刚度计算：根据结构的几何模型和几何约束条件，利用刚度法或变分原理，求解结构的刚度矩阵和刚度方程。

5.结构的位移计算：通过求解结构的刚度方程，得到结构的位移向量，描述结构在载荷作用下的位移的大小和方向。

6.结构的变形分析：根据结构的位移向量和几何约束条件，计算结构的变形矩阵，描述结构在载荷作用下的形变情况。

通过几何组成分析，可以定量描述结构的形态、几何特性及其对结构力学特性的影响。

它既可以作为结构静力分析的一种方法，用于求解结构的刚度、位移和变形等参数；也可以应用于结构动力分析，研究结构在动载荷作用下的动力响应。

几何组成分析在工程实践中具有非常重要的应用价值。

首先，它可以辅助结构工程师进行结构设计和优化，提高结构的稳定性和刚度性能。

其次，在结构检测和维修中，几何组成分析可以用于评估结构的变形和破坏情况，指导结构的维修方案和控制措施。

此外，几何组成分析还可以应用于结构材料的研究和性能表征，为结构材料的选择和设计提供科学依据。

结构的几何组成分析结构的几何组成分析是建筑设计中的一个重要环节，它涉及到结构的形式和几何特征，通过分析结构的几何组成，可以评估结构的稳定性、刚度和性能，并为后续的结构设计提供依据。

以下是对结构的几何组成分析的详细介绍。

1.结构的几何形式结构的几何形式是指结构的整体形状和布局，它包括建筑的平面形式和立面形式。

建筑的平面形式通常是对称的，例如对称轴线、对称平面。

立面形式主要体现建筑的垂直方向的几何特征，包括建筑的高度、层高、外墙的形式等。

通过分析结构的几何形式，可以了解结构的总体布局和形态特征。

2.结构的几何参数结构的几何参数是指结构中各个构件和元件的尺寸和形状，它包括构件的截面形状、长度、宽度、高度等参数。

通过分析结构的几何参数，可以确定结构的尺寸比例，进而评估结构的刚度和稳定性。

例如，在分析桥梁的几何参数时，通过确定桥梁的主跨长度、桥梁墩高和桥梁宽度等参数，可以评估桥梁的刚度和承载能力。

3.结构的几何构造结构的几何构造是指结构中的构件和元件之间的相互连接方式和排列方式。

不同的几何构造方式会影响结构的刚度和稳定性。

常见的几何构造包括平行构造、直交构造、等距构造等。

通过分析结构的几何构造，可以评估结构的整体刚度和受力性能，并为结构的材料选择和构造方式提供依据。

4.结构的几何约束结构的几何约束是指结构中各个构件和元件之间的相互约束关系。

几何约束决定了结构的运动自由度，影响结构的整体稳定性和刚度。

常见的几何约束方式包括铰支约束、弹性支座约束、弹簧约束等。

通过分析结构的几何约束，可以确定结构的运动自由度，进而评估结构的刚度和稳定性。

在进行结构的几何组成分析时，通常采用计算机辅助设计软件进行建模和分析。

通过建立结构的几何模型，可以对结构的几何特征进行精确描述，并对结构的性能进行定量分析。

同时，可以通过调整结构的几何参数和几何构造，优化结构的性能和经济性。

总之，结构的几何组成分析是建筑设计中不可或缺的一个环节，通过对结构的几何形式、几何参数、几何构造和几何约束进行分析，可以评估结构的稳定性、刚度和性能，为结构的后续设计和施工提供依据。

几何组成分析
几何组成分析是几何学中一个相当重要且普遍应用的一个技术，它凭借空间的几何结构及形状，可以帮助人们快速的把复杂的几何图形划分为其组成的几何元素，比如体积、曲面等等，为后续的分析提供了有力的帮助。

几何组成分析的主要步骤包括：首先，利用图形采样技术对空间图形进行采样；其次，利用几何分析技术，进行各个采样点之间的连接；然后，在图形中进行分割和识别，完成形状划分；最后，空间图形拓扑结构化，得到图形的几何元素。

目前，几何组成分析技术在各行各业中得到了广泛的应用，主要用于几何形状的划分及识别，如制造工程中零件的设计、机械工程中机器人识别，以及地理信息系统等。

例如，在精密制造中，几何组成分析可以帮助把复杂的零件形状划分为若干元素，有效提高加工精度和加工效率；而在机器人加工中，几何组成分析还可以帮助机器人识别目标零件的形状，提高机器人加工准确性。

此外，几何组成分析技术也在地理信息系统中被广泛应用，特别是有关城市建筑物、地表尺度及地面走行路线的分析，几何组成分析技术用于对各种尺度的建筑物进行划分，或分析街道、道路和其它地表特征，对地理信息系统的建设及使用有着重要的作用。

总之，几何组成分析技术在几何学及相关领域有着重要的应用潜力，它不仅可以帮助人们快速的把复杂的几何图形划分为其组成的几何元素，还可以在制造、机器人等行业中发挥重要作用，极大的提高
了生产效率、降低了成本，应被广泛的重视及使用。

平面体系的几何组成分析平面体系是指在二维平面上展示和分析的几何结构，可以是二维图形、图表或者平面上的线条、点等。

几何组成分析是对平面体系中组成要素的形态和关系进行研究、描述和解释的过程。

在平面体系的几何组成分析中，主要包括以下几个方面的内容：1.几何形态分析：几何形态分析是对平面体系中的形状、大小、比例关系等几何特征进行分析和描述的过程。

在几何形态分析中，可以通过测量、标注、计算等方法获取图形的尺寸信息，并通过比较、计算等方法揭示出图形的相似性、对称性等几何特征。

2.几何结构分析：几何结构分析是对平面体系中各个组成要素之间的关系进行研究和解释的过程。

在几何结构分析中，可以根据图形之间的相对位置、相互连接关系等，判断图形的层次结构、组合关系等几何关系，并通过分析这些几何关系揭示出图形之间的相互作用和约束关系。

3.几何变换分析：几何变换分析是对平面体系中的图形进行变换、平移、旋转等操作，以研究和揭示几何要素之间的关系和规律的过程。

在几何变换分析中，可以通过变换操作改变图形的形态、位置等几何特征，并观察这些变换对图形的几何关系和性质的影响，进而揭示出图形之间的变换关系和对称性等几何规律。

4.几何拓扑分析：几何拓扑分析是对平面体系中的点、线、面等几何要素之间的拓扑关系进行研究和表示的过程。

在几何拓扑分析中，可以通过判断要素之间的相交、包含、连接等关系，建立起点、边、面等要素之间的拓扑关系，并通过分析这些拓扑关系揭示出图形的几何拓扑特征和性质。

5.几何组合分析：几何组合分析是对平面体系中的各个组成要素进行组合、排列等操作，以研究和描述图形的整体特征和性质的过程。

在几何组合分析中，可以将各个组成要素进行组合或排列，形成新的图形，并通过分析这些组合或排列揭示出图形的组成特征、数量关系等几何特征。

几何组成分析不仅可以帮助我们理解和描述平面体系中的几何特征和规律，还可以应用于许多领域，如建筑设计、工程规划、地理信息系统等。

【例2-3】对如图2-18所示体系进行几何组成分析。

图2-18 例2-3图【解】如图2-18(a)所示体系，分别将曲杆AC、曲杆BD及基础当作刚片Ⅰ、Ⅱ及Ⅲ。

其中，刚片Ⅰ、Ⅲ间通过实铰A相连，刚片Ⅱ、Ⅲ间通过实铰B相连，刚片Ⅰ、Ⅱ间通过链杆CD、EF相连（虚铰在其交点O处）。

三刚片间通过两个实铰A、B及一个虚铰O两两相连，这三铰不共线，形成几何不变体系且无多余约束。

如图2-18(b)所示体系，分别以杆CD、杆AB及基础作为三个刚片：Ⅰ、Ⅱ和Ⅲ。

刚片Ⅰ、Ⅱ间通过平行链杆AC、BD相连（虚铰（Ⅰ, Ⅱ）在无穷远处），刚片Ⅰ、Ⅲ间分别通过C、D处的支座链杆相连（虚铰在结点D处），刚片Ⅱ、Ⅲ间分别通过A、B处的支座链杆相连（虚铰在结点A处）。

三刚片间通过两个有限远虚铰（在结点A和D处）及一个无限远处虚铰（Ⅰ, Ⅱ）两两相连，由于两个有限远处虚铰的连线AD，与形成无穷处虚铰的平行链杆（杆AC、BD）不平行，因此形成的是几何不变体系且无多余约束。

如图2-18(c)所示体系，分别以铰结三角形124、铰结三角形237及杆56作为基本刚片：刚片Ⅰ、Ⅱ和Ⅲ。

刚片Ⅰ、Ⅱ间通过实铰2相连，刚片Ⅰ、Ⅲ间通过平行链杆16、45相连，刚片Ⅱ、Ⅲ间通过平行链杆35、67相连，这两对平行链杆形成的虚铰（Ⅰ,Ⅲ）、（Ⅱ,Ⅲ）均位于无穷远处。

这样，三刚片通过三铰两两相连，其中两铰位于无穷远处，由于形成两个无穷远处虚铰的两对平行链杆不互相平行，因此上部体系为无多余约束的几何不变部分。

上部体系再分别通过三个支座链杆与基础相连，按两刚片规则，形成的整个体系为无多余约束的几何不变体系。

如图2-18(d)所示体系，分别以杆15、36及24作为三个基本刚片Ⅰ、Ⅱ和Ⅲ。

刚片Ⅰ、Ⅱ间通过一对平行链杆13、56相连，刚片Ⅰ、Ⅲ间通过一对平行链杆12、54相连，刚片Ⅱ、Ⅲ通过一对平行链杆23、46相连。

三对平行链杆形成的虚铰均在无穷远处，因而形成的上部体系是几何瞬变体系。