事故树的定量分析
- 格式:ppt
- 大小:911.50 KB
- 文档页数:48
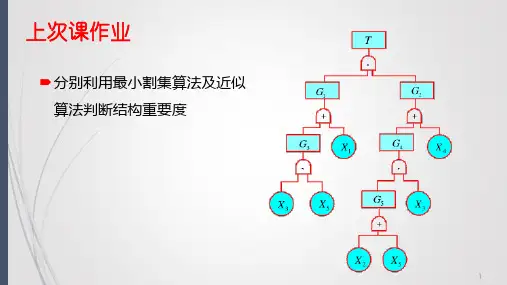










事故树的定性定量分析一、计算题1、某事故树的最小割集为K1={X1,X2,X5};K2={X1,X3,X5};K3={X1,X4,X5},各基本事件的发生概率为q1=q3=q4=0.01,q2=0.1,q5=0.95,求顶上事件发生概率。
2、某事故树的最小割集为K1={X1,X2};K2={X3,X4};K3={X5,X6},各基本事件的发生概率为q1=q2 =0.01,q3=q4=0.02,q5=q6=0.05,求顶上事件发生概率3、某事故树有三个最小径集:P 1={ X1},P 2={ X2,X3},P 3={ X4, X5 ,X6}。
求基本事件的结构重要度。
二、选择题1、某事故树的最小径集为:Pl={Xl,X2,X4},P2={Xl,X2,X5},P3={Xl,X3,X6},P4={Xl,X3,X7},则结构重要程度为()A、I(1)>I(2)=I(3)>I(4)=I(5)B、I(1)>I(2)<I(3)>I(4)=I(5)C、I(1)>I(2)>I(3)<I(4)=I(5)D、I(3)>I(2)<I(1)>I(4)=I(5)三、填空题1、基本事件的概率重要度是指顶上事件发生概率对该基本事件发生概率的()。
2、临界重要度也称(),它是基本事件发生概率的变化率与顶上事件发生概率的变化率的比来确定基本事件的重要程度。
答案:一、1、,本题中最小割集有重复因子,因此需将公式展开后消去重复因子才能带入数据进行计算。
P(T)=q1q2q5+q1q3q5+q1q4q5-(q1q2q3q5+q1q2q4q5+q1q3q4q5)+ q1q2q3q4q5=1.12020 x10-32、本题中最小割集没有重复因子,因此公式不需要展开,直接带数据进行计算。
=1-(1-qK1)·(1-qK2)·(1-qK3)=1-(1-q1q2)(1-q3q4)(1-q5q6)=1.4996x10-3 3、I(1)>I(i) i=2,3 )> I(i)i= 4,5,6二、1、A三、1、变化率;2、危险重要度火力发电厂应当建在哪里我国某大型产煤矿区要建设坑口火力发电厂(p),已知有n 处产煤矿口,并且修建至电厂的运煤轨道的费用与产煤量及距离成正比(W*L ),运用MPA学科中定量分析的方式方法,为坑口火力发电厂选址,要求目标是费用最小。
一、引言随着社会经济的快速发展,各类事故的发生频率也在不断增加,给人民生命财产和社会稳定带来了严重影响。
为了有效预防和控制事故风险,提高应急救援能力,本文将对应急预案事故风险进行定量分析,为制定合理的应急救援措施提供科学依据。
二、事故风险定量分析方法1. 事故树分析法(FTA)事故树分析法是一种系统安全分析方法,通过对事故发生的因果关系进行定性和定量分析,找出事故发生的主要原因。
FTA的基本步骤如下:(1)确定顶事件:顶事件是指事故发生的最终结果,如火灾、爆炸、中毒等。
(2)分析中间事件:中间事件是指导致顶事件发生的原因,如设备故障、操作失误、人为因素等。
(3)分析基本事件:基本事件是指导致中间事件发生的原因,如设备老化、维护不当、操作人员培训不足等。
(4)建立事故树:将基本事件、中间事件和顶事件按照因果关系连接起来,形成事故树。
(5)计算事故发生概率:根据基本事件发生的概率,通过事故树进行定量分析,得出事故发生的概率。
2. 事件树分析法(ETA)事件树分析法是一种基于概率的定量分析方法,通过对事故发生过程中的各种可能事件进行概率计算,预测事故发生的风险。
ETA的基本步骤如下:(1)确定初始事件:初始事件是指事故发生的起点,如设备启动、操作人员接触危险物质等。
(2)分析可能事件:分析初始事件发生后可能出现的各种事件,如正常、异常、故障等。
(3)计算事件概率:根据各种可能事件的概率,计算事故发生的概率。
(4)建立事件树:将各种可能事件按照因果关系连接起来,形成事件树。
(5)计算事故发生概率:根据事件树进行定量分析,得出事故发生的概率。
三、应急预案事故风险定量分析实例以下以某化工厂为例,进行应急预案事故风险定量分析。
1. 确定顶事件:化工厂发生火灾。
2. 分析中间事件:火灾发生的原因包括设备故障、操作失误、人为因素等。
3. 分析基本事件:设备老化、维护不当、操作人员培训不足等。
4. 建立事故树:将基本事件、中间事件和顶事件按照因果关系连接起来,形成事故树。