r(r=1,2, … ,k) 相互独立, 可 以证明其对立事件E/r 也是独立事件, 则有:
对于式(3-25), 由于 Xi=O( 不发生 ) 的概率接近于 1, 故不适用 于最小径集的计算 ,否则误差较大。
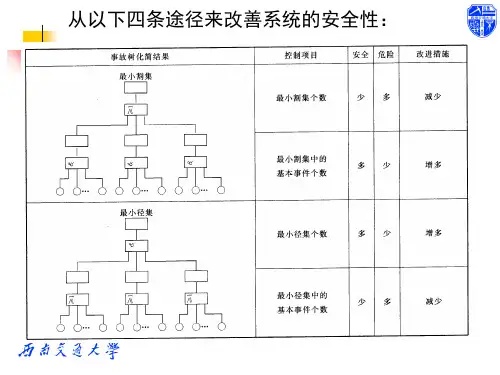
重要度分析
一个基本事件对顶事件发生的影响大小称为该基本事件的重要 度。重要度分析在系统的事故预防、事故评价和安全性设计等方面 有着重要的作用。事故树中各基本事件的发生对顶事件的发生有着 程度不同的影响, 这种影响主要取决于两个因素 , 即各基本事件发 生概率的大小以及各基本事件在事故树模型结构中处于何种位置。 为了明确最易导致顶事件发生的事件, 以便分出轻重缓急采取有效 措施,控制事故的发生, 必须对基本事件进行重要度分析。
事故树定量分析
用 “与门” 连接的顶事件的发生概率为: 用 “或门” 连接的顶事件的发生概率为: 式中 qi -- 第 i 个基本事件的发生概率 ( i=1,2, … , n)。 如图 3-15所示的事故树。已知各基本事 件的发生概率q1 =q2 =q3 =0.1, 顶事件的 发生概率为: P (T) = q1[1-(1- q2)(1- q3)] = 0.1[1-(1-0.1)(1-0.1)] = 0.019
事故树定量分析 例:以图事故树为例, 试用最小割集 法、最小径集法计算顶事件的发生概 率。 各基本事件发生的概率分别为:q1 =0.01; q2=0.02; q3=0.03; q4=0.04; q5=0.05 解:事故树有三个最小割集:K1={ X1, X2, X3} , K2={ X1, X4}, K3={ X3, X5} 事故树有四个最小径集: P1={X1, X3,}; P2={X1, X5}; P3={X3, X4}; P4={X2, X4, X5}
事故树定量分析