当前位置：文档之家 › 理想介质中的平面波

理想介质中的平面波

  • 格式：ppt
  • 大小：1002.00 KB
  • 文档页数：29

下载文档原格式

  / 29

合集下载

【高中物理】优质课件：理想介质中的均匀平面波

【高中物理】优质课件：理想介质中的均匀平面波


E y
k2
E y
,
d2 d
H z x2
k 2H z
式中 k j j —传播常数 ( propagation constant)，
通解 E y E e j x E e j x
H z
H e j x H e j x
1 (E ej x E e j x ) Z0
2 —波数、相位常数 ( phase constant) rad/m ，
特点：Ey 和 Ez 振幅相同，相位差90°。
合成后 E Ey2 Ez2 C 即 Ey2 Ez2 C2
tanα Ez tan( t )
Ey
Ey 超前 Ez 为右旋极化波。 Ey 滞后 Ez 为左旋极化波。
图6.4.2 圆极化的平面波
返回 上页 下页
椭圆极化（Elliptical Polarization)
返回 上页 下页
感 谢 观 看
H z H ze xe j x H ze xe j x
振幅呈指数衰减,电磁波是减幅波。
当 ，称为良导体， ' ，忽略位移电流。 j
k2 j , k j (1 j) 1 (1 j)
2
d
1 2d
返回 上页 下页
良导体中波的传播特性： E , H 为减幅波（集肤效应) ； 波阻抗为复数, E 超前 H 45
图6.2.1 理想介质中正弦均匀 平面波沿 x 方向的传播
返回 上页 下页
例 6.2.1 自由空间中 B 106 cos(6π 108t 2πz)(ex ey ) 试求：a. f ,v,, 及传播方向；b. E 和 S。
解：a. 波沿 z 轴方向传播; 2π rad/m
2π 1 m f 2π 3108 Hz
无界理想介质中均匀平面波传播特点

无界理想介质中均匀平面波传播特点

无界理想介质中均匀平面波传播特点一、介质的概念和分类介质是指电磁波传播的物质媒介，包括空气、水、金属等。

根据介质的性质，可以将其分为导体和绝缘体两种。

导体是一种能够导电的物质，其内部存在自由电子，并且能够吸收和散射电磁波；绝缘体则是一种不能导电的物质，其内部不存在自由电子，对电磁波具有反射、折射和透射等性质。

二、无界理想介质中均匀平面波的定义无界理想介质是指在空间中没有边界限制，并且不存在任何形式的损耗或散射的理想介质。

均匀平面波是指在空间中具有相同振幅和相位，并且沿着同一方向传播的平面波。

三、无界理想介质中均匀平面波传播特点1. 传播速度恒定：在无界理想介质中，均匀平面波沿着一个方向传播时，其速度始终保持不变。

这是因为在理想情况下不存在任何形式的损耗或散射，因此波的传播速度保持恒定。

2. 波长和频率关系：在无界理想介质中，均匀平面波的波长和频率之间存在一定的关系。

根据电磁波的传播公式，速度等于频率乘以波长，因此当频率增加时，波长会相应地减小。

3. 透射和反射：在无界理想介质中，均匀平面波遇到边界时会发生透射和反射。

如果边界是一个绝缘体，则电磁波会被反射回来；如果边界是一个导体，则电磁波会被吸收。

而当均匀平面波从一个介质进入另一个介质时，也会发生透射和反射现象。

4. 极化方向：在无界理想介质中，均匀平面波的极化方向与传播方向垂直。

这意味着在水平传播的电磁波中，电场垂直于传播方向；而在竖直传播的电磁波中，电场则沿着传播方向。

5. 衍射效应：当均匀平面波遇到障碍物或孔径时，会发生衍射现象。

衍射效应是电磁波传播中的一种重要现象，它使得电磁波能够绕过障碍物或通过孔径。

四、总结在无界理想介质中，均匀平面波的传播特点主要包括传播速度恒定、波长和频率关系、透射和反射、极化方向以及衍射效应等。

这些特点对于电磁波的传播和应用具有重要意义，深入了解其特性可以帮助我们更好地理解电磁波的本质和原理。

第六章-平面波详解

第六章-平面波详解


E exEx ey Ey
两个分量可以表示成为
Ex

E e jkz jx xm
Ey

E e jkz jy ym
第六章 平面波
合成场矢量E可以写为
E ex Exme jkz jx ey Eyme jkz jy
瞬时值表达式分别为
Ex Exm cos(t kz x ) Ey Eym cos(t kz y ) E ex Exm cos(t kz x ) ey Eym cos(t kz y )
E2

1 4

E02e2az
第六章 平面波
平均磁能密度：
wav,m

1 4
H
2

1 4
E02
2
f
e2az

1 4

E02
e2
az
1 ( )2
总的平均能量密度：
wav

wav,e

wav,m

1 4

E02e2
z

1 4

E02e2
z
1 ( )2

1 4

E E
Ex2

E
2 y

Em
合成场矢量E与x轴正方向的夹角α为

arctan
Ey Ex

arctan

sin(t cos(t
x x
) )


(t

x
)
圆极化波有左旋和右旋之分，规定如下：
将大拇指指向电磁波的传播方向，其余四指指向电
第六章 平面波
场矢量E矢端的旋转方向，若符合右手螺旋关系，则 称之为右旋圆极化波；
42-理想介质中的均匀平面波

42-理想介质中的均匀平面波


2H 1 2H x 2 v 2 t 2
上式是理想介质中均匀平面波的方程。
将电磁场基本方程式在直角坐标系中展开，得
2019/10/3
华北电力大学电气与电子工程学院
9
工程电磁场
主讲人： 王泽忠
( Hz y

H z
y
)e
x
( H x z

H z x
)e y
( H y x
H yey 和 H zez 是 H 的两个分量。
3．理想介质中均匀平面波的传播
一维波动方程，以 E y 和 Hz 为例，其通解为
Ey x, t f1 t x / v f2 t x / v

E
y

x,
t


Ey

x,
t

2019/10/3
华北电力大学电气与电子工程学院
华北电力大学电气与电子工程学院
4
工程电磁场
H E t
E H t
H 0
主讲人： 王泽忠
E 0 前两个方程中，每个方程都含有 E 和 H ，
可将上述方程综合成只含有一个变量的方程式。
对第 2 个方程式取旋度得
2019/10/3
华北电力大学电气与电子工程学院
6
工程电磁场
2E


2E t 2
用同样的方法，可得
主讲人： 王泽忠
2H


2H t 2
将 v 1 代入式，得
2E

1 v2
2E t 2
2019/10/3
华北电力大学电气与电子工程学院
7
工程电磁场
第六章-平面波详解

第六章-平面波详解

Exm Eym Em
x y
2
则
Ex Em cos(t x )
E y Em cos(t x ) Em sin(t x ) 2
第六章 平面波
合成场矢量E的大小为
2 E E Ex2 E y Em
合成场矢量E与x轴正方向的夹角α为
合成场矢量E的大小为
2 2 2 2 E E Ex Ey Exm E ym cos(t )
合成场矢量E与x轴正方向的夹角α为
arctan
Ey Ex arctan Eym Exm 常数
第六章 平面波
同理，假设 Ex 和 Ey 两个分量反相，即 φx-φy=π ，则合 成场矢量E的大小为


2 1 ( ) 1 2
导电介质的波阻抗
f 1/ 2 (1 j ) f e j f j
第六章 平面波
相速
vp dz 1 [ dt 1 ]1/ 2 1 ( )2 1 2
第六章 平面波
平面电磁波 : 等相面为平面的电磁波，并且它的等相 面是与电磁波的传播方向相垂直的无限大平面。平面 电磁波简称为平面波，它是矢量波动方程的一个特解。 均匀平面波 : 对于平面波而言，如果其等相面无限大， 而且等相面上各点的场强大小相等、方向相同，即沿 着某个传播方向的平面波的场量除了与时间有关之外， 只与电磁波传播方向的坐标有关，而与其它方向的坐 标无关，即平面波的电场和磁场只沿着波的传播方向 变化，而在等相面内电场和磁场的方向、振幅以及相
arctan
Ey sin(t x ) arctan (t x ) Ex cos(t x )
理想介质中的均匀平面电磁波

理想介质中的均匀平面电磁波


(x,
t)
g1(t
x) v
g
2(t
x) v
v 1
f1 、f2 、g1 、g2 的具体形式与产生该波的 激励方式有关。
一、一维波动方程的解及其物理意义
E
y
(x,
t)
E
y
(x,
t
)
E
y
(x,
t)
f 1(t
x) v
f 2(t
x) v
H
z
(x, t)
H
z
(x,
t)
H
z
(x,
t)
g1(t
x) v
一、一维波动方程的解及其物理意义
E
y
(x,
t)
E
y
(x,
t
)
E
y
(x,
t)
f 1(t
x) v
f 2(t
x) v
H
z
(x, t)
H
z
(x,
t)
H
z
(x,
t)
g1(t
x) v
g2 (t
x) v
v 1
入射波和反射波：
理想介质中均匀平面波的传播速度是一常数。
1
v
c
c
rr n
n rr 称为介质的折射率。
2. 理想介质中的正弦均匀平面波
电场强度和磁场强度在时间上同相，振幅比为实数 电磁波无衰减地传播，是等振幅波 相位因子，相速等于波速且与频率无关
2 H H 2 H
x2
t
t 2
0
x22E
E t
2 E t 2
0
这两个一维波动方程的解分别为
第8章 平面电磁波

第8章 平面电磁波


时间相位变化 所经历的时间称为电磁波的周期 周期， 表示， 时间相位变化 2π 所经历的时间称为电磁波的周期，以 T 表示，而 的次数称为频率 频率， 表示。 一秒内相位变化 2π 的次数称为频率，以 f 表示。那么由 ωT = 2π的关系 式，得 2π 1 T= = ω f 所经过的距离称为波长 波长， 表示。 空间相位 kz 变化 2π 所经过的距离称为波长，以 λ 表示。那么由关 系式 kλ = 2π，得 2π λ= k 由上可见，电磁波的频率是描述相位随时间的变化特性， 波长描述相 由上可见，电磁波的频率是描述相位随时间的变化特性，而波长描述相 频率是描述相位随时间的变化特性 位随空间的变化特性。 空间的变化特性 位随空间的变化特性。
由关系式 H y = j ∂E x 可得
ωµ ∂z
Hy =
ε E x 0 e − jkz = H y 0 e − jkz µ
式中
H y0 =
ε E x0 µ
可见， 理想介质中 均匀平面波的电场与磁场相位相同 介质中， 相位相同， 可见，在理想介质中，均匀平面波的电场与磁场相位相同，且两者 有关，但振幅不会改变。 空间相位均与变量 z 有关，但振幅不会改变。
此式称为齐次矢量亥姆霍兹方程， 此式称为齐次矢量亥姆霍兹方程，式中 齐次矢量亥姆霍兹方程
k = ω µε
在直角坐标系中，可以证明， 在直角坐标系中，可以证明，电场强度 E 及磁场强度 H 的各个分 量分别满足下列方程： 量分别满足下列方程：
∇ 2 Ex (r ) + k 2 Ex (r ) = 0 2 2 ∇ E y (r ) + k E y (r ) = 0 2 2 ∇ Ez (r ) + k Ez (r ) = 0 ∇ 2 H x (r ) + k 2 H x (r ) = 0 2 2 ∇ H y (r ) + k H y (r ) = 0 2 2 ∇ H z (r ) + k H z (r ) = 0
理想介质中的均匀平面波

理想介质中的均匀平面波

（3）坡印廷矢量和平均坡印廷矢量。
解：由已知条件可知：频率: f 100MHz
(1) vp
振幅: Ex0 104V / m 1 1 1 3 108 m / s
r r 00 2
k 2 108 2 108 4
3
3
l 2 1.5m
k
(2)设 E ex E0 cos(t kz 0 )
0
0 0
4 107 120 377()
1 109
36
在自由空间中传播的电磁波，电场幅度与磁场幅度之比为377。
能量密度和能流密度
实数表达形式
电场能量密度： we
1 2
E2
磁场能量密度：wm
1 2
H
2
1 2
(
E)2 1 E2
2
we wm
结论：理想媒质中均匀平面波的电场能量等于磁场能量。
z
1 2
Re
ex 50e-
jkz
ey
50 377
e
jkz
ez
1 2
2500 377
W
m2
垂直穿过半径R=2.5m的圆平面的平均功率为
P
S
S平均
dS
S平均
R2
2500 2.52
2 377
65.11
W
例
空气中传播的均匀平面波的电场为 E ez E0e j(3x4 y)
试求:(1)波的传播方向； (2)波的频率和波长； (3)与E相伴的磁场H；(4)坡印廷矢量和平均坡印廷矢量； (5)波的能量密度。
k exkx eyky ezkz , r exx ey y ez z 则：k r (exkx eyky ezkz )(exx ey y ez z)
(整理)第十八讲：理想介质中的均匀平面波

(整理)第十八讲：理想介质中的均匀平面波

5.1理想介质中的均匀平面电磁波3、理解和掌握均匀平面波在无界理想介质中的传播特性。

重点：1）波的表示方法；2）均匀平面波在无界理想介质中的传播特性。

难点：均匀平面波在无界理想介质中的传播特性。

讲授、练习2学时第五章均匀平面电磁波在无界空间中的传播变化着的电场和磁场互相激发，形成在空间中传播的电磁波。

电磁波已在广播通讯、光学和其它科学技术中得到广泛应用。

前面一章已经从麦克斯韦方程组出发导出了电磁场的波动方程，从本章开始到第七章我们将分别讨论电磁波在无界、半无界及有界空间中的传播规律和特点。

本章研究对象与内容如下：研究对象：无界空间中的电磁波主要内容：1、均匀平面电磁波在无界的理想介质和导电媒质中的传播特性；2、电磁波的极化；3、均匀平面电磁波在各向异性媒质中的传播（自学）；4、相速与群速。

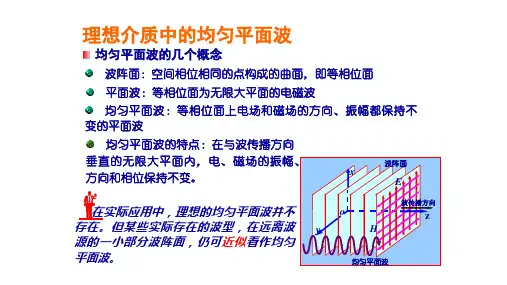
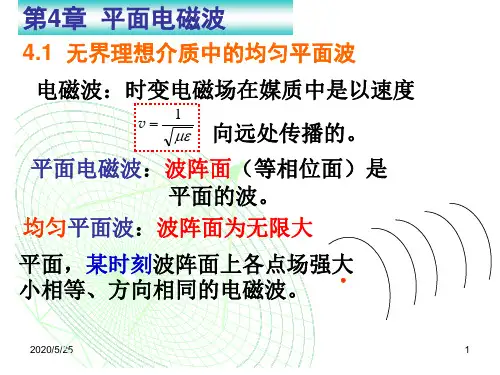
授课学时：6学时5.1理想介质中的均匀平面电磁波平面电磁波是指电磁波沿某一方向传播，其波阵面为与传播方向垂直的平面。

均匀平面波是指电磁波的场矢量只沿着它的传播方向变化，在与传播方向垂直的无限大平面内，场矢量的方向、振幅、相位都保持不变。

均匀平面波是一种理想化的模型，但它又能表征电磁波的重要和主要性质，并且在某些情况下实际波可以近似看作均匀平面波，因此研究均匀平面波既有理论意义又有实用价值。

一、理想介质中均匀平面波函数设电磁波沿z 轴方向传播，并且在z =常数的平面上各点场矢量都相同（均匀平 面电磁波），即：()(),,E r t E z t =、()(),,H r t H z t =与,x y 无关，即：0E E x y ∂∂==∂∂， 0H Hx y∂∂==∂∂ 同时，由0E ∇⋅=和0H ∇⋅=，有：0z E z ∂=∂， 0zH z∂=∂ 再根据波动方程(亥姆霍兹方程)，有： 220E k E ∇+=0z z E H ==即均匀平面波的电矢量和磁矢量都与传播方向垂直，这种波称为横电磁波（TEM 波）。

此时电磁场满足的亥姆霍兹方程为：()()2220i i d E z k E z dz +=， ()()2220i i d H z k H z dz+=(),i x y = 其特解： 1212,j j jkz jkz m m A e e A e e φφ-（im A 为常量），分别代表沿z 轴正向和负向传播的无损耗的单色均匀平面波。

7.1-7.2_波动方程_理想介质中平面波及偏振

7.1-7.2_波动方程_理想介质中平面波及偏振

简振的一维电场有形式解：
见 P178
电磁场与电磁波
z Ex f t v
相位因子
7
同理：简振的一维电场有另一种形式解：
z Ex f t v
综合考虑入射波(z方向)和反射波(反方向)：
z z Ex f t f t v v
Ex 2 k Ex 0 2 z
2
2H y z 2
k 2H y 0
标量亥姆霍兹方程
电磁场与电磁波
16
均匀平面波的标量解
2 Ex k 2 Ex 0 z 2 2 2
k
E x E0 e
jkz
e jkz E0
－z方向,反射波
＋z方向,入射波
H J D t
——交变的电场产生交变的磁场。 E dl B t dS E B t
C S
——交变磁场又产生交变的电场。 这种交变的电场、磁场互相产生的现象无限地 循环下去。
于是它们脱离场源，由近及远地传播出去，我 们把这种波动着的电磁场称为电磁波。
E0 E0 j(t kz ) j(t kz ) e e / /
17
波动方程的解
H j E E j H H 0 E 0
Maxwell Eq. Helmholtz eq.
E x ( r , t ) E0 e j (t kz ) H y( r , t ) H 0 e j (t kz ) H y (r , t ) 1



E x (r , t )

k k x ex k y e y k z ez
4.1无界理想介质中的均匀平面波

4.1无界理想介质中的均匀平面波


对于正弦电磁场，复数形式的波动方程为：
E E 0
2 2
复数不加“
”
若为平面波，则上式可写为： （假定电场只有x分量）
Ex 2 k Ex 0 2 z
2
其通解为：
Ex E e
- jkz m
E e
m
jkz
(4.8)
考虑式（4.8）右边第一项，正是式（4.5） 的复数形式。
2019/1/14 2
于是电场的波动方程为
Ex Ex 0 2 2 z t
2 2
（4.1）
该方程的通解为
1 E x f1 z t f2 z t （4.2） 1
f1和f2是任意函数，将(3.2)代入(3.1)，通解满 足电场的波动方程.
jkz j jkz j 1 1 3 3 Re ex 4e ey e 2 10 1 ez W / m2 5
2019/1/14
18
Ex Ex Ex



Ey Ey Ey



1
入、反 射波
Hy Hy Hy
3、入射波－－沿 反射波－－沿
2019/1/14
z 轴方向以速度 z轴方向以速度 v
Hx Hx Hx
v
1
传播。 传播。
10
4、电场和磁场相位 相同，振幅不同， 电场振幅比磁场振 幅大 倍
jkz jt E ( z , t ) Re( E e e ) E 有： x m m cos(t kz )
2019/1/14 7
无界空间没有反射波，电场可写为：

电磁场与电磁波课件7.1 无限大理想介质中的均匀平面波


S av ( ： z)

S ( z ) R e ( E H ) a v
设
j j k z e E a Ee a E e e xx 0

j k z 0 x x
j k z j j k z e H a He a H ee 0 y y y y 0
2
令
k
2 2 2
dE z ) 2 x( E z )0 x( 2 dz
2

其中:
为传播常数;
为相位常数.
在此其与波数k相同
j
rad m
实数
方程的解：

() z e E E
x x 0



z
e E


z x 0
E x E x0 e E x0 e
8 x
2 2 rad /m
1
2
即
j (t z) E(z, t) Im[ ax 20 2e ] jz jt Im[ ax 20 2e e ] Im[ ax 20 e
复振幅 jz jt
2

e
]
复有效 j 2 z x 值 E ( z ) a 20 e (V/m) x x 由于电场（x)、磁场、传播方向(z)符 合右手螺旋定则：故磁场为 y 方向。
E 1 1 1 2 w( zt , ) H zt ,) E y ( x 2 2 2
则 故
w ( z , t ) w ( z , t ) e m
对均匀平面波来说, 电场能量密度与磁场能量密 度相等。

5 理想介质的均匀平面波

2
4
2 2 E E E 2 2 2 2 k E 0 x y z 2 Ex 2 Ex 2 Ex 2 k Ex 0 2 2 2 y z x 2 Ey 2 Ey 2 Ey 2 k 2 Ey 0 x y 2 z 2 2 2 2 Ez Ez Ez 2 x 2 y 2 z 2 k Ez 0
同理可以推得： E
H k
12
从公式可知：均匀平面电磁波中电场幅度和磁场幅度 之比为一定值。定义电场幅度和磁场幅度比为媒质本征 阻抗，用 表示，即：
E ＝ ——媒质本征阻抗 H
7
特殊地：真空（自由空间）的本振阻抗为：
0 0 0
结论：在自由空间中传播的电磁波，电场幅度与磁场 幅度之比为377。 13
1

讨论：1、电磁波传播的相位速度仅与媒质特性相关。
2、真空中电磁波的相位速度：
1 9 4 10 10 36 8 v p 0 3 10 ( m/ s c 光速) ) (
7
vp0
1
0 0

1
真空中电磁波相位速度为光速。
11
3、 =
1 f

vp f
vp f
4 10 120 377() 1 9 10 36
说明： E H k H 1 E、 、k 三者相互垂直，且满 H k E 足右手螺旋关系。

6、能量密度和能流密度
实数表达形式
1 2 电场能量密度： we E 2 1 2 1 2 1 2 磁场能量密度：wm H ( E) E 2 2 2 we wm

§61均匀平面波在理想介质中的传播

在理想介质中，散射系数通常是一个恒定的值，表 示波在单位路径上受到的散射程度。
吸收系数
吸收系数描述了波在传播过程中能量被介质吸收 的程度。
吸收系数与介质的电导率、磁导率和介电常数等 因素有关。
在理想介质中，吸收系数通常是一个恒定的值， 表示波在单位路径上被吸收的能量。
散射与吸收的物理机制
散射机制
当波遇到介质中的微小粒子时，粒子会将部分波的能量反射回周围空间，形成 散射现象。散射的程度取决于粒子的尺寸、形状和分布情况。
吸收机制
当波在介质中传播时，介质中的分子或原子会与波相互作用，将部分波的能量 转化为热能或其他形式的能量，导致波的能量逐渐减少。吸收的程度取决于介 质的电导率、磁导率和介电常数等因素。
根据不同介质界面，菲涅尔公式有不同的形式， 但都反映了能量守恒和边界条件。
应用范围
适用于理想介质和非理想介质，是研究波传播的重要工具。
04
均匀平面波的散射与吸收
散射系数
01
散射系数描述了波在传播过程中受到介质中微小粒 子散射的程度。
02
散射系数与介质的微观结构、波长以及入射角度等 因素有关。
03
高频电磁波在真空中的传播
高频电磁波
01
高频电磁波是指频率较高的电磁波，如可见光、紫外线和X射线
等。
真空中的传播
02
在真空中，由于没有介质吸收和散射，高频电磁波可以以光速
传播。
电磁场
03
高频电磁波是由变化的电场和磁场相互激发而传播的。
低频声波在液体中的传播
低频声波
低频声波是指频率较低的声波，如次声波。
能量与功率流密度
能量密度
在理想介质中，均匀平面波的能量密度是指单位 时间内通过单位面积的能量。

理想介质中的平面波解

理想介质中的平面波若介质中的传导电流与位移电流相比完全可以忽略，这样的介质称为理想介质，或称为完全介质、无损耗介质(σ = 0)。

由前面，我们有：220ωμε∇+=E E令22k ωμε=对于给定频率，它是一个常数。

由此得：220k ∇+=E E此方程称为其次亥姆霍兹矢量方程。

由此我们得到三个其次亥姆霍兹标量方程：220x x E k E ∇+= 220y y E k E ∇+=220z z E k E ∇+=现在，我们用分离变量法先求解第一个方程。

令(,,)()()()x x E E x y z X x Y y Z z ==将其带入第一个方程，并除以XYZ ，我们得到：22222221d 1d 1d 0d d d X Y Zk X Y Z x y z+++= 重新整理为：22222221d 1d 1d d d d X Y Z k X Y Z x y z ++=- 上式左边仅是x 和y 的函数，而右边仅是z 的函数，它们相等只能说明它们等于同样一个常数。

我们将此常数写为2z k 。

因此，我们得到：222d 0d z Zk Z z+= 重复此过程，我们还可得到：222d 0d x Xk X x+= 222d 0d y Y k Y y+= 2x k 和2yk 也是常数。

三个分离变量常数k x 、k y 和 k z 并不全是独立的，它们满足： 2222x y z k k k k ++=由于我们仅对行波解感兴趣，对于前行波，场的相位随坐标变量的增加而延迟。

因此，我们得到上面方程前行波解为：x y z ik x f ik yf ik zf X X e Y Y eZ Z e ===下标表示前行（forward-traveling ）即有：i x xf E E e =k x式中E xf = X f Y f Z f 。

同样地有：i y yf E E e =k x i z zf E E e =k x式中E xf 、E yf 和E zf 为积分常数。

理想介质中的平面波(中文)


由上求得 式中
vp 1 f f 0 0
0 f
1
0 0
0 r r
rr 0
0 为平面波在真空中传播时的波长。
0 的现象称为波长缩短效应，或简称为缩
波效应。 由 H y 可j 得Ezx
Hy
Ex0e
jkz
H
e jkz
y0
H y0
E x0
可见，在理想介质中，电场与磁场相位相同， 且两者空间相位均与变量 z 有关，但振幅不会改变。
Ex
Hy
1 Z
ez
Ex
z
或
E x ZH y ez
Hy
对于传播方向而言，电场及磁场仅具有横向
分量，因此称为横电磁波，或称为 TEM 波。以后
将会遇到在传播方向上具有电场或磁场分量的非
TEM 波。
T－
均匀平面波是TraTnEsvMer波se ，只有非均匀平面波
才 可形成非 TEM 波，但是 TEM 波也可以是非均
均匀平面波的波面是无限大的平面，波面上各点的 场强振幅又均匀分布，因而波面上各点的能流密度相 同，可见这种均匀平面波具有无限大的能量。因此， 实际中不可能存在这种均匀平面波。
当观察者离开波源很远时，因波面很大，若观察 者 仅限于局部区域，则可以近似作为均匀平面波。
利用空间傅里叶变换，可将非平面波展开为很多 平面波之和。

H (z)
1 Z0
ez
E
ey
1 6π
e
j2πz
A/m
③
Sc
E
H*
e z
10 3π
W/m2
④
vp ve
3108 m/s
k
电磁波的波段划分及其应用

9.1.5理想介质中的均匀平面波+-+问题-09-1-2

问题-09-1-2 在理想介质中，对于某已知的正弦均匀平面电磁波，如何判断其传播方向？其电场强度与磁场强度的大小和方向满足怎样的关系？
问题解答：在理想介质中，对于某已知的正弦均匀平面电磁波，主要通过
正弦函数中相位的时空关系也就是等相位面的传播特性进行判断。

具体而言，（1）对于时域表达的正弦均匀平面电磁波，当相位的时空关系为(ωt -kx) 时，其传播方向为+x方向。

当相位的时空关系为(ωt +kx) 时，其传播方向为-x 方向；（2）对于复数表达的正弦均匀平面电磁波，当相位因子为e-jkx 时，其传播方向为+x 方向。

当相位因子为e+jkx 时，其传播方向为-x 方向。

正弦均匀平面电磁波的电场强度与磁场强度的大小之比为理想介质的特性阻抗，电场强度方向、磁场强度方向、传播方向三者依次满足右手正交关系。

参考资料：1、王泽忠主编，《工程电磁场》，清华大学出版社
2、倪光正主编，《工程电磁场原理》，高等教育出版社
关键词：理想介质中的均匀平面电磁波、电磁波的波阻抗。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平面波的参数 Ex (t) E0 cos(t kz)
空间相位kz变化2π所经过的距离称为波长或相位波长, 以λ表
示。 由kλ=2π得
k 2
k称为波数, 因为, 空间相位变化2π相当于一个全波, k表示单位
长度内所具有的全波数目。
时间相位ωt变化2π所经历的时间称为周期, 以T表示; 而一秒 内相位变化2π的次数称为频率, 用f表示。因ωT=2π, 得
即一个波长对应 2
2.
平面波在空间某点z=z0处的Ex与t的关系曲线 如图。 由图可以看出， 均匀平面波在空间 任意观察点处， 其场强是以角频率ω随时间 按正弦规律变化的。当t增加一个周期T， ωT=2π， 场强恢复其初始的大小和相位。
Ex
T
z＝z0
0
t
电场与时间的关系
空间固定点（如z=0）电场随时间振荡
f 1 T 2
等相面(波前)传播的速度称为相速。我们来考察波前上的一个
特定点, 这样的点对应于cos(ωt-kz)=const. 即ωt-kz=const., 由此可得
ωdt-kdz=0, 故相速为
vp
dz dt
k
1
Ex t1 t2
(t2＞t1)
0
z
对于真空,
vp
1
0 0
1
3 108m / s c
电磁波的磁场强度:
ex ey ez
H j E j
x
y
z
ey
j
Ex z
Ex 0 0
ey
j（
jk）E0e jkz
ey
k
E0e jkz
ey
E0
e jkz
/
η具有阻抗的量纲, 单位为欧姆(Ω), 它的值与媒质的参数有关, 因 此它被称为媒质的波阻抗。在真空中
0
1
36
109 F
/ m, 0
式中E0是z=0处电场强度的振幅。ωt称为时间相位, kz称为空间相 位。 空间相位相同的场点所组成的曲面称为等相面（波前或波 面）。 可见, z=const.的平面为波面。因此称这种电磁波为平面电 磁波。 又因Ex与x, y无关, 在z=const.的波面上各点场强相等。这 种在波面上场强均匀分布的平面波称为均匀平面波。它是最基本 的电磁波形式。
r r
3.
由于平面波在任意给定的时刻（t=t0）， 其波形 随距离z按正弦波变化， 如图所示。 因此， 任 意给定时刻, 相位相差2π的两平面间的距离λ称 为波长(Wave length)， kλ=2π
2 , k 2
k
Ex
t＝t0
0 z
电磁波的波长
6.2.3 平面波的传播特性
Ex ex E0e jkz
它是横波, 称为横电磁波 TEM(Transverse Electro-Magnetic)波。
(2) E, H处处同相, 二者振幅之比为媒质的波阻抗η(实数)。
(3) 复坡印廷矢量为:
S
1 2
E H*
1 2
xˆE0e jkz
yˆ
E0
e jkz
zˆ 1 2
E02
S av
a)均匀平面波沿传播方向传输实功率, 无虚功率。
反射波
对应的瞬时值为
Ex E0 cos(t kz) E0' cos(t kz)
+z方向
－z方向
+Z方向传播的电磁波的瞬时波形
Ex
t＝t0
0 z
固定时刻，电场随传播方向的变化
Ex
T
z＝z0
0
t
固定位置，电场随时间振荡
6.2.2 平面波的参数
电场复振幅和瞬时值可表示为
Ex E0e jkz, Ex (t) E0 cos(电磁场
标量波动方程:
2Ex k2Ex 0, k
设Ex仅与坐标z有关而与x, y无关, 则
2
2 x2
2 y 2
2 z 2
2 z 2
化为
d 2Ex dz2
k2Ex
0
这是二阶常微分方程, 其解为
Ex
Ex
Ex
Em e jkz
Eme
jkz
入射波
4
107 H
/m
0 0 /0 377 120 ()
即
H
1
ez
E
E ez H
此关系为均匀平面波的电场E和磁场H的互换关系（一维）。
x (Ex)
S
E
O z
H
y
(Hy)
无耗媒质中传播的均匀平面波及电场E、 磁场H与S的关系
x (Ex)
S
E
O z
H y (Hy)
沿z轴传播的平面波坐标关系
(1) E, H互相垂直, 并与传播方向 zˆ 垂直, 即都无纵向分量, 因此
行波既然是一个行进的波， 那么， 必然 可以找到一个物理量来表示其行进的速度。
我们定义平面波的等相位面移动的速度称为相 速(Phase Velocity)， 所谓等相位面即满足下 列关系的平面
ωt-kz= 将上式两边对时间t微分， 整理得行波的相速：
p
dz dt
k
1
• 相速还可以表示为
p
c n
,n
(b) xz平面上的瞬时E和H(S=E×H处处指向传播方向)
沿任意方向传播的平面波:
1
H es E E es H
es E 0 es H 0
利用此法求例题7.1
例 电磁波在真空中传播，其电场强度矢量的复数表达式为
E (ex jey )104 e j20 z (V / m)
试求： (1) 工作频率f; (2) 磁场强度矢量的复数表达式； (3) 坡印廷矢量的瞬时值和时间平均值；
场强也随z变化。 图给出的是不同时刻t1和 t2(t2>t1)的电场对距离z的关系曲线。 由图可 见， 在任一固定时刻， 场强随距离z同样按 正弦规律变化， 且随着时间的推移， 函数的
各点沿+z方向向前移动， 因此称之为行波 (Traveling Wave)。
Ex t1 t2
(t2＞t1)
0
z 电场与距离z的关系
4 107 1 109
36
可见, 电磁波在真空中的相速等于真空中的光速。
小结：平面波的参数:
1.
t kz
代表了场的波动状态，称为电磁波的相位。其中，ωt表 示随时间变化部分； -kz表示随空间距离变化部分。
令t=t0， 作出相位φ与传播方向z的关系：
0
z
相位与传输距离的关系
说明：波的相位沿传播 方向呈连续的线性滞后， 滞后系数为K(rad/m)，
b)平均功率密度为常数，表明与传播方向垂直的所有平面上，
每单位面积通过的平均功率都相同，电磁波在传播过程中没有能
量损失(沿传播方向电磁波无衰减)。因此理想媒质中的均匀平面电
磁波是等振幅波。
平面波的传播特性 E exE0e jkz H eyH0e jkz
均匀平面波的电磁场分布 (a) 某一时刻E和H沿z轴的变化(E和H相互垂直, 同相);