北邮概率论与数理统计统计量及其分布(6.3)
- 格式:doc
- 大小:717.50 KB
- 文档页数:13

概率论与数理统计课后答案北邮版(第三章)(总18页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题三1.将一硬币抛掷三次,以X表示在三次中出现正面的次数,以Y表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X和Y的联合分布律.222⨯⨯222⨯⨯=2.盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球,以X表示取到黑球的只数,以Y表示取到红球的只数.求X和Y的联合分布律.【解】和的联合分布律如表:223247C3C35=313247C2C35=11232247C C6C35=21132247C C12C35=313247C2C35=12132247C C6C35=223247C3C35=3.设二维随机变量(X,Y)的联合分布函数为F(x,y)=⎪⎩⎪⎨⎧≤≤≤≤.,020,2,sinsin其他ππyxyx求二维随机变量(X,Y)在长方形域⎭⎬⎫⎩⎨⎧≤<≤<36,4πππyx内的概率.【解】如图πππ{0,}(3.2)463P X Y<≤<≤公式ππππππ(,)(,)(0,)(0,)434636F F F F--+ππππππsin sin sin sin sin0sin sin0sin4346361).4=--+=题3图说明:也可先求出密度函数,再求概率。
4.设随机变量(X ,Y )的分布密度f (x ,y )=⎩⎨⎧>>+-.,0,0,0,)43(其他y x A y x e求:(1) 常数A ;(2) 随机变量(X ,Y )的分布函数;(3) P {0≤X <1,0≤Y <2}. 【解】(1) 由-(34)0(,)d d e d d 112x y A f x y x y A x y +∞+∞+∞+∞+-∞-∞===⎰⎰⎰⎰得 A =12 (2) 由定义,有 (,)(,)d d yxF x y f u v u v -∞-∞=⎰⎰(34)340012ed d (1e )(1e )0,0,0,0,y yu v x y u v y x -+--⎧⎧-->>⎪==⎨⎨⎩⎪⎩⎰⎰其他(3) {01,02}P X Y ≤<≤<12(34)3800{01,02}12e d d (1e )(1e )0.9499.x y P X Y x y -+--=<≤<≤==--≈⎰⎰5.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<<--.,0,42,20),6(其他y x y x k(1) 确定常数k ;(2) 求P {X <1,Y <3}; (3) 求P {X <};(4) 求P {X +Y ≤4}. 【解】(1) 由性质有242(,)d d (6)d d 81,f x y x y k x y y x k +∞+∞-∞-∞=--==⎰⎰⎰⎰故 18R =(2) 13{1,3}(,)d d P X Y f x y y x -∞-∞<<=⎰⎰130213(6)d d 88k x y y x =--=⎰⎰ (3) 11.5{ 1.5}(,)d d a (,)d d x D P X f x y x y f x y x y <<=⎰⎰⎰⎰如图1.5402127d (6)d .832x x y y =--=⎰⎰(4) 24{4}(,)d d (,)d d X Y D P X Y f x y x y f x y x y +≤+≤=⎰⎰⎰⎰如图b240212d (6)d .83xx x y y -=--=⎰⎰题5图6.设X 和Y 是两个相互独立的随机变量,X 在(0,)上服从均匀分布,Y 的密度函数为f Y (y )=⎩⎨⎧>-.,0,0,55其他y y e求:(1) X 与Y 的联合分布密度;(2) P {Y ≤X }.题6图【解】(1) 因X 在(0,)上服从均匀分布,所以X 的密度函数为1,00.2,()0.20,.X x f x ⎧<<⎪=⎨⎪⎩其他 而55e ,0,()0,.y Y y f y -⎧>=⎨⎩其他所以(,),()()X Y f x y X Y f x f y 独立5515e25e,00.20,0.20,0,yy x y --⎧⎧⨯<<>⎪==⎨⎨⎩⎪⎩且其他. (2) 5()(,)d d 25e d d y y x DP Y X f x y x y x y -≤≤=⎰⎰⎰⎰如图0.20.2-550-1d 25e d (5e 5)d =e 0.3679.xyx x y x-==-+≈⎰⎰⎰7.设二维随机变量(X ,Y )的联合分布函数为F (x ,y )=⎩⎨⎧>>----.,0,0,0),1)(1(24其他y x y x e e求(X ,Y )的联合分布密度.【解】(42)28e ,0,0,(,)(,)0,x y x y F x y f x y x y -+⎧>>∂==⎨∂∂⎩其他. 8.设二维随机变量(X ,Y )的概率密度为f (x ,y )= 4.8(2),01,0,0,.y x x y x -≤≤≤≤⎧⎨⎩其他求边缘概率密度. 【解】()(,)d X f x f x y y +∞-∞=⎰x204.8(2)d 2.4(2),01,=0,.0,y x y x x x ⎧⎧--≤≤⎪=⎨⎨⎩⎪⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰12y 4.8(2)d 2.4(34),01,=0,.0,y x x y y y y ⎧-⎧-+≤≤⎪=⎨⎨⎩⎪⎩⎰其他题8图 题9图9.设二维随机变量(X ,Y )的概率密度为f (x ,y )=e ,0,0,.y x y -⎧<<⎨⎩其他求边缘概率密度. 【解】()(,)d X f x f x y y +∞-∞=⎰e d e ,0,=0,.0,y x x y x +∞--⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰0e d e ,0,=0,.0,yy x x y y --⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他题10图10.设二维随机变量(X ,Y )的概率密度为f (x ,y )=22,1,0,.cx y x y ⎧≤≤⎨⎩其他(1) 试确定常数c ;(2) 求边缘概率密度. 【解】(1)(,)d d (,)d d Df x y x y f x y x y +∞+∞-∞-∞⎰⎰⎰⎰如图2112-14=d d 1.21xx cx y y c ==⎰⎰ 得214c =. (2) ()(,)d X f x f x y y +∞-∞=⎰212422121(1),11,d 840,0,.x x x x x y y ⎧⎧--≤≤⎪⎪==⎨⎨⎪⎪⎩⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰522217d ,01,420,0,.y y x y x y y -⎧⎧≤≤⎪⎪==⎨⎨⎪⎪⎩⎩其他 11.设随机变量(X ,Y )的概率密度为f(x,y)=1,,01, 0,.y x x⎧<<<⎨⎩其他求条件概率密度f Y|X(y|x),f X|Y(x|y).题11图【解】()(,)dXf x f x y y+∞-∞=⎰1d2,01,0,.xxy x x-⎧=<<⎪=⎨⎪⎩⎰其他111d1,10,()(,)d1d1,01,0,.yY yx y yf y f x y x x y y-+∞-∞⎧=+-<<⎪⎪⎪===-≤<⎨⎪⎪⎪⎩⎰⎰⎰其他所以|1,||1,(,)(|)2()0,.Y XXy xf x yf y x xf x⎧<<⎪==⎨⎪⎩其他|1,1,1(,)1(|),1,()10,.X YYy xyf x yf x y y xf y y⎧<<⎪-⎪⎪==-<<⎨+⎪⎪⎪⎩其他12.袋中有五个号码1,2,3,4,5,从中任取三个,记这三个号码中最小的号码为X,最大的号码为Y.(1)求X与Y的联合概率分布;(2)X与Y是否相互独立【解】(1)X与Y的联合分布律如下表345{}iP X x= YX1 3511C 10= 3522C 10= 3533C 10= 610 2 0 3511C 10= 3522C 10= 310 32511C 10= 110{}i P Y y =110 310 610(2) 因6161{1}{3}{1,3},101010010P X P Y P X Y ===⨯=≠=== 故X 与Y 不独立13.设二维随机变量(X ,Y )的联合分布律为 2 5 8(1)求关于X 和关于Y 的边缘分布;(2) X 与Y 是否相互独立2 5 8 P {Y=y i }{}i P X x =(2) 因{2}{0.4}0.20.8P X P Y ===⨯0.160.15(2,0.4),P X Y =≠=== 故X 与Y 不独立.14.设X 和Y 是两个相互独立的随机变量,X 在(0,1)上服从均匀分布,Y 的概率密度为f Y (y )=⎪⎩⎪⎨⎧>-.,0,0,212/其他y y e(1)求X 和Y 的联合概率密度;(2) 设含有a 的二次方程为a 2+2Xa +Y =0,试求a 有实根的概率.【解】(1) 因1,01,()0,X x f x <<⎧==⎨⎩其他; 21e ,1,()20,yY y f y -⎧>⎪==⎨⎪⎩其他.故/21e01,0,(,),()()20,.y X Y x y f x y X Y f x f y -⎧<<>⎪=⎨⎪⎩独立其他XYX Y题14图(2) 方程220a Xa Y ++=有实根的条件是2(2)40X Y ∆=-≥故 X 2≥Y , 从而方程有实根的概率为:22{}(,)d d x yP X Y f x y x y ≥≥=⎰⎰21/2001d e d 212[(1)(0)]0.1445.x y x yπ-==Φ-Φ=⎰⎰15.设X 和Y 分别表示两个不同电子器件的寿命(以小时计),并设X 和Y 相互独立,且服从同一分布,其概率密度为f (x )=⎪⎩⎪⎨⎧>.,0,1000,10002其他x x求Z =X /Y 的概率密度.【解】如图,Z 的分布函数(){}{}Z XF z P Z z P z Y=≤=≤ (1) 当z ≤0时,()0Z F z =(2) 当0<z <1时,(这时当x =1000时,y =1000z)(如图a) 3366102222101010()d d d d yz Z zx y zF z x y y x x y x y +∞≥==⎰⎰⎰⎰ 33610231010=d 2z zy yzy +∞⎛⎫-= ⎪⎝⎭⎰题15图 (3) 当z ≥1时,(这时当y =103时,x =103z )(如图b )3366222210101010()d d d d zy Z x y zF z x y y x x yx y +∞≥==⎰⎰⎰⎰ 336231010101=d 12y y zy z +∞⎛⎫-=- ⎪⎝⎭⎰即 11,1,2(),01,20,.Z z z zf z z ⎧-≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他故 21,1,21(),01,20,.Z z z f z z ⎧≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他16.设某种型号的电子管的寿命(以小时计)近似地服从N (160,202)分布.随机地选取4只,求其中没有一只寿命小于180h 的概率.【解】设这四只寿命为X i (i =1,2,3,4),则X i ~N (160,202),从而123412{min(,,,)180}{180}{180}i P X X X X X P X P X ≥≥≥之间独立34{180}{180}P X P X ≥≥1234[1{180}][1{180}][1{180}][1{180}]P X P X P X P X =-<-<-<-<44144180160[1{180}]120[1(1)](0.158)0.00063.P X ⎡-⎤⎛⎫=-<=-Φ ⎪⎢⎥⎝⎭⎣⎦=-Φ== 17.设X ,Y 是相互独立的随机变量,其分布律分别为P {X =k }=p (k ),k =0,1,2,…, P {Y =r }=q (r ),r =0,1,2,….证明随机变量Z =X +Y 的分布律为P {Z =i }=∑=-ik k i q k p 0)()(,i =0,1,2,….【证明】因X 和Y 所有可能值都是非负整数,所以 {}{}Z i X Y i ==+={0,}{1,1}{,0}X Y i X Y i X i Y =====-==于是{}{,},i k P Z i P X k Y i k X Y =====-∑相互独立0{}{}ik P X k P Y i k ===-∑()()ik p k q i k ==-∑18.设X ,Y 是相互独立的随机变量,它们都服从参数为n ,p 的二项分布.证明Z =X +Y 服从参数为2n ,p 的二项分布.【证明】方法一:X +Y 可能取值为0,1,2,…,2n .{}{,}ki P X Y k P X i Y k i =+====-∑00202(){}2ki ki n i k i n k ii k k n k i k n k P X i P Y k i n n p q p qi k i n n p qi k i n p q k =---+=-=-===-⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭⎛⎫⎛⎫= ⎪⎪-⎝⎭⎝⎭⎛⎫= ⎪⎝⎭∑∑∑方法二:设μ1,μ2,…,μn ;μ1′,μ2′,…,μn ′均服从两点分布(参数为p ),则X =μ1+μ2+…+μn ,Y =μ1′+μ2′+…+μn ′, X +Y =μ1+μ2+…+μn +μ1′+μ2′+…+μn ′,所以,X +Y 服从参数为(2n ,p )的二项分布.(2) 求V =max (X ,Y )的分布律; (3) 求U =min (X ,Y )的分布律;(4) 求W =X +Y 的分布律.【解】(1){2,2}{2|2}{2}P X Y P X Y P Y ======5{2,2}0.051,0.252{,2}i P X Y P X i Y ========∑ {3,0}{3|0}{0}P Y X P Y X P X ======3{0,3}0.011;0.033{0,}j P X Y P X Y j ========∑ (2){}{max(,)}{,}{,}P V i P X Y i P X i Y i P X i Y i ====<+≤=10{,}{,},i ik k P X i Y k P X k Y i -=====+==∑∑ 0,1,2,3,4,5i =所以V 的分布律为(3) {}{min(,)}P U i P X Y i ===351{,}{,}{,}{,}k ik i P X i Y i P X i Y i P X i Y k P X k Y i ==+==≥+>====+==∑∑0,1,2,3,i =(1) 求P {Y >0|Y >X };(2) 设M =max{X ,Y },求P {M >0}.题20图【解】因(X ,Y )的联合概率密度为22221,,(,)π0,.x y R f x y R⎧+≤⎪=⎨⎪⎩其他 (1){0,}{0|}{}P Y Y X P Y Y X P Y X >>>>=>0(,)d (,)d y y xy xf x y f x y σσ>>>=⎰⎰⎰⎰π2π/405π42π/401d d π1d d πRR r rR r r R θθ=⎰⎰⎰⎰3/83;1/24==(2) {0}{max(,)0}1{max(,)0}P M P X Y P X Y >=>=-≤00131{0,0}1(,)d 1.44x y P X Y f x y σ≤≤=-≤≤=-=-=⎰⎰21.设平面区域D 由曲线y =1/x 及直线y =0,x =1,x=e 2所围成,二维随机变量(X ,Y )在区域D 上服从均匀分布,求(X ,Y )关于X 的边缘概率密度在x =2处的值为多少题21图【解】区域D 的面积为 22e e 0111d ln 2.S x x x===⎰(X ,Y )的联合密度函数为211,1e ,0,(,)20,.x y f x y x ⎧≤≤<≤⎪=⎨⎪⎩其他(X ,Y )关于X 的边缘密度函数为1/2011d ,1e ,()220,.x X y x f x x⎧=≤≤⎪=⎨⎪⎩⎰其他 所以1(2).4X f =22.设随机变量X 和Y 相互独立,下表列出了二维随机变量(X ,Y )联合分布律【解】因21{}{,}j j iji P Y y P P X x Y y ======∑,故11121{}{,}{,},P Y y P X x Y y P X x Y y ====+== 从而11111{,}.6824P X x Y y ===-= 而X 与Y 独立,故{}{}{,}i j i i P X x P Y y P X x Y y =====,从而11111{}{,}.624P X x P X x Y y =⨯==== 即:1111{}/.2464P X x ===又1111213{}{,}{,}{,},P X x P X x Y y P X x Y y P X x Y y ====+==+==即1,3111{},4248P X x Y y =++== 从而131{,}.12P X x Y y === 同理21{},2P Y y == 223{,}8P X x Y y ===又31{}1j j P Y y ===∑,故3111{}1623P Y y ==--=.同理23{}.4P X x == 从而23313111{,}{}{,}.3124P X x Y y P Y y P X x Y y ====-===-=故23.设某班车起点站上客人数X 服从参数为λ(λ>0)的泊松分布,每位乘客在中途下车的概率为p (0<p <1),且中途下车与否相互独立,以Y 表示在中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率;(2)二维随机变量(X ,Y )的概率分布.【解】(1) {|}C (1),0,0,1,2,m m n mn P Y m X n p p m n n -===-≤≤=.(2) {,}{}{|}P X n Y m P X n P Y m X n ======e C (1),,0,1,2,.!m m n mnnp p n m n n n λλ--=-≤≤=24.设随机变量X 和Y 独立,其中X 的概率分布为X ~⎪⎪⎭⎫⎝⎛7.03.021,而Y 的概率密度为f (y ),求随机变量U =X +Y 的概率密度g (u ).【解】设F (y )是Y 的分布函数,则由全概率公式,知U =X +Y 的分布函数为(){}0.3{|1}0.7{|2}G u P X Y u P X Y u X P X Y u X =+≤=+≤=++≤=0.3{1|1}0.7{2|2}P Y u X P Y u X =≤-=+≤-=由于X 和Y 独立,可见()0.3{1}0.7{2}G u P Y u P Y u =≤-+≤-0.3(1)0.7(2).F u F u =-+-由此,得U 的概率密度为()()0.3(1)0.7(2)g u G u F u F u '''==-+-0.3(1)0.7(2).f u f u =-+-25. 设随机变量X 与Y 相互独立,且均服从区间[0,3]上的均匀分布,求P {max{X ,Y }≤1}.解:因为随即变量服从[0,3]上的均匀分布,于是有1, 03,()30, 0,3;x f x x x ⎧≤≤⎪=⎨⎪<>⎩ 1, 03,()30, 0, 3.y f y y y ⎧≤≤⎪=⎨⎪<>⎩ 因为X ,Y 相互独立,所以1, 03,03,(,)90, 0,0,3, 3.x y f x y x y x y ⎧≤≤≤≤⎪=⎨⎪<<>>⎩ 推得 1{max{,}1}9P X Y ≤=.26. 设二维随机变量(X ,Y )的概率分布为1 0 11 0 1 a 0 b 0 c其中a ,b ,c 为常数,且X 的数学期望E (X )=,P {Y ≤0|X ≤0}=,记Z =X +Y .求:(1) a ,b ,c 的值; (2) Z 的概率分布; (3) P {X =Z }.解 (1) 由概率分布的性质知,a+b+c +=1 即 a+b+c = . 由()0.2E X =-,可得0.1a c -+=-.再由 {0,0}0.1{00}0.5{0}0.5P X Y a b P Y X P X a b ≤≤++≤≤===≤++,得 0.3a b +=.解以上关于a ,b ,c 的三个方程得0.2,0.1,0.1a b c ===.(2) Z 的可能取值为2,1,0,1,2,X Y{2}{1,1}0.2P Z P X Y =-==-=-=,{1}{1,0}{0,1}0.1P Z P X Y P X Y =-==-=+==-=,{0}{1,1}{0,0}{1,1}0.3P Z P X Y P X Y P X Y ===-=+==+==-=,{1}{1,0}{0,1}0.3P Z P X Y P X Y ====+===,{2}{1,1}0.1P Z P X Y =====,即Z 2 1 0 1 2(3) {}{0}0.10.20.10.10.20.4P X Z P Y b ====++=++=.27. 设随机变量X,Y 独立同分布,且X 的分布函数为F(x),求Z=max{X,Y}的分布函数.解:因为X,Y 独立同分布,所以F X (z )=F Y (z),则F Z (z )=P{Z ≤z}=P{X ≤z ,Y ≤z}=P{x ≤z}·P{Y ≤z}=[F (z )]2.28.设随机变量X 与Y 相互独立,X 的概率分布为1{},1,0,1,3P X i i ===-Y 的概率密度为1,01,()0,Y y f y ≤<⎧=⎨⎩其他.记Z =X +Y .(1)求1{|0};2P Z X ≤= (2)求Z 的概率密度()Z f z分析 题(1)可用条件概率的公式求解.题(2)可先求Z 的分布函数,再求导得密度函数.解(1) 1{0,}12{|0}2{0}P X Z P Z X P X =≤≤===1{0,}2{0}P X Y P X =≤== 11{}22P Y =≤=(2)(){}{}Z F z P Z z P X Y z =≤=+≤{,1}{,0}{,1}P X Y z X P X Y z X P X Y z X =+≤=-++≤=++≤= {1,1}{,0}{1,1}P Y z X P Y z X P Y z X =≤+=-+≤=+≤-= {1}{1}{}{0}{1}{1}P Y z P X P Y z P X P Y z P X =≤+=-+≤=+≤-=1[{1}{}{1}]3P Y z P Y z P Y z =≤++≤+≤-1[(1)()(1)]3Y Y Y F z F z F z =+++-'1()()[(1)()(1)]3Z Z Y Y Y f z F z f z f z f z ==+++-1,1230,.z ⎧-≤<⎪=⎨⎪⎩其他29.设随机变量(X,Y)服从二维正态分布,且X 与Y 不相关,f X (x),f Y (y)分别表示X,Y 的概率密度,求在Y=y 的条件下,X 的条件概率密度f X |Y (x |y).解:由第四章第三节所证可知,二维正态分布的不相关与独立性等价,所以f(x,y)=f X (x) ·F Y (y),由本章所讨论知,/()()(,)(/)()()()X Y X Y X Y Y f x f y f x y f x y f x f y f y ===.30.设二维随机变量(X ,Y )的概率密度为2,01,01,(,)0,.x y x y f x y --<<<<⎧=⎨⎩其他(1)求{2};P X Y >(2)求Z =X +Y 的概率密度()Z f z .分析 已知(X,Y)的联合密度函数,可用联合密度函数的性质{(,)P X Y ∈}(,)GG f x y dxdy =⎰⎰ 解(1); Z=X+Y 的概率密度函数可用先求Z 的分布函数再求导的方法或直接套公式求解. 解 (1)2{2}(,)x yP X Y f x y dxdy >>=⎰⎰120120(2)57().824x dx x y dyx x dx =--=-=⎰⎰⎰(2)()(,),Z f z f x z x dx +∞-∞=-⎰其中 2()01,01(,)0x z x x z x f x z x ---<<<-<⎧-=⎨⎩其他201,01z x z x -<<<-<⎧=⎨⎩其他当02z z ≤≥或时,()0Z f z =; 当01z <<时,0()(2)(2);zZ f z z dx z z =-=-⎰ 当12z ≤<时,121()(2)(2),Z z f z z dx z -=-=-⎰即Z 的概率密度为2(2)01()(2)120Z z z z f z z z -<<⎧⎪=-≤<⎨⎪⎩其他。


概率论与数理统计教案-统计量和抽样分布一、教学目标1. 理解统计量的概念,掌握常见统计量的计算方法。
2. 了解抽样分布的定义,掌握正态分布、t分布、卡方分布等常见抽样分布的特点及应用。
3. 学会使用抽样分布进行假设检验和置信区间的估计。
二、教学内容1. 统计量的概念及计算方法统计量的定义样本均值、样本方差、样本标准差等常见统计量2. 抽样分布的定义及特点抽样分布的定义正态分布、t分布、卡方分布等常见抽样分布的特点3. 抽样分布的应用假设检验置信区间的估计三、教学方法1. 讲授法:讲解统计量的概念、计算方法,抽样分布的定义及特点。
2. 案例分析法:通过具体案例,让学生学会使用抽样分布进行假设检验和置信区间的估计。
3. 互动教学法:引导学生参与课堂讨论,提问、解答问题,提高学生的积极性和主动性。
四、教学步骤1. 引入统计量的概念,讲解样本均值、样本方差、样本标准差等常见统计量的计算方法。
2. 讲解抽样分布的定义,介绍正态分布、t分布、卡方分布等常见抽样分布的特点及应用。
3. 通过具体案例,让学生学会使用抽样分布进行假设检验和置信区间的估计。
五、课后作业1. 复习本节课的内容,整理笔记。
2. 完成课后习题,加深对统计量和抽样分布的理解。
3. 选择一个感兴趣的话题,运用抽样分布进行实际问题的分析。
六、教学评估1. 课堂提问:通过提问了解学生对统计量和抽样分布的理解程度。
2. 课后习题:检查学生对课堂内容的掌握情况。
3. 实际案例分析:评估学生运用抽样分布解决实际问题的能力。
七、拓展与延伸1. 引导学生探讨抽样分布在其他领域的应用,如经济学、生物学等。
2. 介绍与抽样分布相关的高级主题,如非参数统计、贝叶斯统计等。
3. 鼓励学生参加相关竞赛、研究项目,提高实践能力。
八、教学资源1. 教材:概率论与数理统计相关教材。
2. 课件:PPT课件,辅助学生理解统计量和抽样分布的概念及应用。
3. 案例资料:提供具体案例,方便学生学会使用抽样分布进行假设检验和置信区间的估计。

概率论与数理统计课后答案北邮版(第四章)(总18页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题四1.设随机变量X 的分布律为X ??1 0 12P 1/8 1/2 1/81/4求E (),(),(2+3). 【解】(1) 11111()(1)012;82842E X =-⨯+⨯+⨯+⨯= (2) 2222211115()(1)012;82844E X =-⨯+⨯+⨯+⨯=(3) 1(23)2()32342E X E X +=+=⨯+=2.已知100个产品中有10个次品,求任意取出的5个产品中的次品数的数学期望、方差. X 0 1 2 3 4 5P 5905100C 0.583C = 1410905100C C 0.340C = 2310905100C C 0.070C = 3210905100C C 0.007C = 4110905100C C 0C = 5105100C 0C = 故 ()0.58300.34010.07020.00730405E X =⨯+⨯+⨯+⨯+⨯+⨯ 0.501,= 52()[()]iii D X x E X P ==-∑222(00.501)0.583(10.501)0.340(50.501)00.432.=-⨯+-⨯++-⨯=3.X ??1 01P p 1 p 2 p 3且已知E ()=,()=,求1,2,3. 【解】因1231P P P ++=……①,又12331()(1)010.1E X P P P P P =-++=-=……②,222212313()(1)010.9E X P P P P P =-++=+=……③由①②③联立解得1230.4,0.1,0.5.P P P ===4.袋中有N 只球,其中的白球数X 为一随机变量,已知E (X )=n ,问从袋中任取1球为白球的概率是多少【解】记A ={从袋中任取1球为白球},则(){|}{}Nk P A P A X k P X k ===∑全概率公式1{}{}1().NNk k k P X k kP X k N Nn E X N N========∑∑5.设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧≤≤-<≤.,0,21,2,10,其他x x x x求E (X ),D (X ). 【解】12201()()d d (2)d E X xf x x x x x x x +∞-∞==+-⎰⎰⎰21332011 1.33x x x ⎡⎤⎡⎤=+-=⎢⎥⎢⎥⎣⎦⎣⎦122232017()()d d (2)d 6E X x f x x x x x x x +∞-∞==+-=⎰⎰⎰ 故 221()()[()].6D XE X E X =-= 6.设随机变量X ,Y ,Z 相互独立,且E (X )=5,E (Y )=11,E (Z )=8,求下列随机变量的数学期望. (1) U =2X +3Y +1;(2) V =YZ ??4X .【解】(1) [](231)2()3()1E U E X Y E X E Y =++=++ 25311144.=⨯+⨯+=(2) [][4][]4()E V E YZ X E YZ E X =-=- ,()()4()Y Z E Y E Z E X -因独立1184568.=⨯-⨯=7.设随机变量X ,Y 相互独立,且E (X )=E (Y )=3,D (X )=12,D (Y )=16,求E(3X ??2Y ),D (2X ??3Y ). 【解】(1) (32)3()2()3323 3.E X Y E X E Y -=-=⨯-⨯=(2) 22(23)2()(3)412916192.D X Y D X DY -=+-=⨯+⨯=8.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<<.,0,0,10,其他x y x k试确定常数k ,并求E (XY ). 【解】因101(,)d d d d 1,2xf x y x y x k y k +∞+∞-∞-∞===⎰⎰⎰⎰故k =2 1()(,)d d d 2d 0.25xE XY xyf x y x y x x y y +∞+∞-∞-∞===⎰⎰⎰⎰.9.设X ,Y 是相互独立的随机变量,其概率密度分别为f X (x )=⎩⎨⎧≤≤;,0,10,2其他x x f Y (y )=(5)e ,5,0,.y y --⎧>⎨⎩其他求E (XY ).【解】方法一:先求X 与Y 的均值 12()2d ,3E X x x x ==⎰ 5(5)5()e d 5e d e d 51 6.z y y z z E Y y yz z z +∞+∞+∞=-----=+=+=⎰⎰⎰令由X 与Y 的独立性,得2()()()6 4.3E XY E X E Y ==⨯=方法二:利用随机变量函数的均值公式.因X 与Y 独立,故联合密度为(5)2e ,01,5,(,)()()0,,y X Y x x y f x y f x f y --⎧≤≤>==⎨⎩其他 于是11(5)2(5)552()2ed d 2de d 6 4.3y y E XY xy x x y x xy y +∞+∞----===⨯=⎰⎰⎰⎰10.设随机变量X ,Y 的概率密度分别为f X (x )=⎩⎨⎧≤>-;0,0,0,22x x x e f Y (y )=⎩⎨⎧≤>-.0,0,0,44y y y e 求(1) E (X +Y );(2) E (2X ??3Y 2). 【解】22-200()()d 2e d [e]e d xx x X X xf x x x x x x +∞+∞+∞--+∞-∞==-⎰⎰⎰201e d .2x x +∞-==⎰401()()d 4e dy .4y Y E Y yf y y y +∞+∞--∞==⎰⎰22242021()()d 4e d .48y Y E Y y f y y y y +∞+∞--∞====⎰⎰从而(1)113()()().244E X Y E X E Y +=+=+=(2)22115(23)2()3()23288E X Y E X E Y -=-=⨯-⨯= 11.设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧<≥-.0,0,0,22x x cx xke 求(1) 系数c ;(2) E (X );(3) D (X ). 【解】(1) 由222()d ed 12k x cf x x cx x k+∞+∞--∞===⎰⎰得22c k =. (2) 222()()d()2e d k x E X xf x x x k x x +∞+∞--∞==⎰⎰22220π2ed .k x kx x +∞-==⎰(3) 222222201()()d()2e .kxE X x f x x x k x k+∞+∞--∞==⎰⎰故 222221π4π()()[()].24D X E X E X k k k⎛-=-=-= ⎝⎭ 12.袋中有12个零件,其中9个合格品,3个废品.安装机器时,从袋中一个一个地取出(取出后不放回),设在取出合格品之前已取出的废品数为随机变量X ,求E (X )和D (X ).【解】设随机变量X 表示在取得合格品以前已取出的废品数,则X 的可能取值为0,1,2,3.为求其分布律,下面求取这些可能值的概率,易知9{0}0.750,12P X === 39{1}0.204,1211P X ==⨯= 329{2}0.041,121110P X ==⨯⨯= 3219{3}0.005.1211109P X ==⨯⨯⨯= 于是,得到的概率分布表如下:X0 1 2 3 P由此可得()00.75010.20420.04130.0050.301.E X =⨯+⨯+⨯+⨯=22222222()075010.20420.04130.0050.413()()[()]0.413(0.301)0.322.E X D X E X E X =⨯+⨯+⨯+⨯==-=-=13.一工厂生产某种设备的寿命X (以年计)服从指数分布,概率密度为f (x )=⎪⎩⎪⎨⎧≤>-.0,0,0,414x x xe为确保消费者的利益,工厂规定出售的设备若在一年内损坏可以调换.若售出一台设备,工厂获利100元,而调换一台则损失200元,试求工厂出售一台设备赢利的数学期望.【解】厂方出售一台设备净盈利Y 只有两个值:100元和??200元 /41/411{100}{1}e d e 4x P Y P X x +∞--==≥==⎰1/4{200}{1}1e .P Y P X -=-=<=-故1/41/41/4()100e (200)(1e )300e 20033.64E Y ---=⨯+-⨯-=-= (元).14.设X 1,X 2,…,X n 是相互独立的随机变量,且有E (X i )=μ,D (X i )=σ2,i =1,2,…,n ,记∑==n i i S X n X 12,1,S 2=∑=--n i i X X n 12)(11. (1) 验证)(X E =μ,)(X D =n2σ;(2) 验证S 2=)(11122∑=--ni i X n X n ;(3) 验证E (S 2)=σ2.【证】(1) 1111111()()().n nn i i i i i i E X E X E X E X nu u n n n n ===⎛⎫===== ⎪⎝⎭∑∑∑22111111()()n nni i i ii i i D X D X D X X DXn nn ===⎛⎫== ⎪⎝⎭∑∑∑之间相互独立2221.n n nσσ==(2) 因222221111()(2)2nnnniii ii i i i i XX X X X X X nX X X ====-=+-=+-∑∑∑∑2222112nniii i XnX X nX X nX ===+-=-∑∑故22211()1ni i S X nX n ==--∑.(3) 因2(),()i i E X u D X σ==,故2222()()().i i i E X D X EX u σ=+=+ 同理因2(),()E X u D X nσ==,故222()E X u nσ=+.从而222221111()()[()()]11n ni i i i E s E X nX E X nE X n n ==⎡⎤=-=-⎢⎥--⎣⎦∑∑221222221[()()]11().1ni i E X nE X n n u n u n n σσσ==--⎡⎤⎛⎫=+-+=⎢⎥ ⎪-⎝⎭⎣⎦∑15.对随机变量X 和Y ,已知D (X )=2,D (Y )=3,Cov(X ,Y )=??1,计算:Cov (3X ??2Y +1,X +4Y ??3).【解】Cov(321,43)3()10Cov(,)8()X Y X Y D X X Y D Y -++-=+- 3210(1)8328=⨯+⨯--⨯=-(因常数与任一随机变量独立,故Cov(X ,3)=Cov(Y ,3)=0,其余类似).16.设二维随机变量(X ,Y )的概率密度为f (x ,y )=221,1,π0,.x y ⎧+≤⎪⎨⎪⎩其他试验证X 和Y 是不相关的,但X 和Y 不是相互独立的. 【解】设22{(,)|1}D x y x y =+≤.2211()(,)d d d d πx y E X xf x y x y x x y +∞+∞-∞-∞+≤==⎰⎰⎰⎰ 2π1001=cos d d 0.πr r r θθ=⎰⎰同理E (Y )=0. 而 Cov(,)[()][()](,)d d X Y x E x y E Y f x y x y +∞+∞-∞-∞=--⎰⎰222π1200111d d sin cos d d 0ππx y xy x y r r r θθθ+≤===⎰⎰⎰⎰, 由此得0XY ρ=,故X 与Y 不相关. 下面讨论独立性,当|x |≤1时,2212112()1.ππx X x f x y x ---- 当|y |≤1时,2212112()1ππy Y y f y x y ---. 显然()()(,).X Y f x f y f x y ≠故X和Y不是相互独立的.17.??1 0 1??111/8 1/8 1/81/8 0 1/81/8 1/81/8验证X和Y是不相关的,但和不是相互独立的.【解】联合分布表中含有零元素,X与Y显然不独立,由联合分布律易求得X,Y及XY的分布律,其分布律如下表X??101P382838Y??101P382838XY??101P284828由期望定义易得E(X)=E(Y)=E(XY)=0.从而E(XY)=E(X)·E(Y),再由相关系数性质知ρXY=0,即X与Y的相关系数为0,从而X和Y是不相关的.又331{1}{1}{1,1}888P X P Y P X Y=-=-=⨯≠==-=-从而X与Y不是相互独立的.18.设二维随机变量(X,Y)在以(0,0),(0,1),(1,0)为顶点的三角形区域上服从均匀分布,求Cov(X,Y),ρXY.【解】如图,S D=12,故(X,Y)的概率密度为题18图2,(,),(,)0,x y Df x y∈⎧=⎨⎩其他.XY()(,)d d DE X xf x y x y =⎰⎰11001d 2d 3x x x y -==⎰⎰22()(,)d d DE X x f x y x y =⎰⎰112001d 2d 6xx x y -==⎰⎰从而222111()()[()].6318D XE X E X ⎛⎫=-=-= ⎪⎝⎭同理11(),().318E Y D Y == 而 1101()(,)d d 2d d d 2d .12xDDE XY xyf x y x y xy x y x xy y -====⎰⎰⎰⎰⎰⎰所以1111Cov(,)()()()123336X Y E XY E X E Y =-=-⨯=-. 从而 112)()XY D Y ρ-===-19.设(X ,Y )的概率密度为f (x ,y )=1ππsin(),0,0,2220.x y x y ,⎧+≤≤≤≤⎪⎨⎪⎩其他求协方差Cov (X ,Y )和相关系数ρXY . 【解】π/2π/21π()(,)d d d sin()d .24E X xf x y x y x xx y y +∞+∞-∞-∞==+=⎰⎰⎰⎰ππ2222201ππ()d sin()d 2.282E X x x x y y =+=+-⎰⎰从而222ππ()()[()] 2.162D XE X E X =-=+-同理 2πππ(),() 2.4162E Y D Y ==+- 又 π/2π/2π()d sin()d d 1,2E XY x xy x y x y =+=-⎰⎰故 2ππππ4Cov(,)()()()1.2444X Y E XY E X E Y -⎛⎫⎛⎫=-=--⨯=- ⎪ ⎪⎝⎭⎝⎭222222π4(π4)π8π164.πππ8π32π8π32)()2162XY D Y ρ-⎛⎫- ⎪--+⎝⎭===-=-+-+-+- 20.已知二维随机变量(X ,Y )的协方差矩阵为⎥⎦⎤⎢⎣⎡4111,试求Z 1=X ??2Y 和Z 2=2X ??Y 的相关系数.【解】由已知知:D (X )=1,D (Y )=4,Cov(X ,Y )=1.从而12()(2)()4()4Cov(,)1444113,()(2)4()()4Cov(,)414414,D Z D X Y D X D Y X Y D Z D X Y D X D Y X Y =-=+-=+⨯-⨯==-=+-=⨯+-⨯=12Cov(,)Cov(2,2)Z Z X Y X Y =--2Cov(,)4Cov(,)Cov(,)2Cov(,)2()5Cov(,)2()215124 5.X X Y X X Y Y Y D X X Y D Y =--+=-+=⨯-⨯+⨯=故 12122)()Z Z D Z ρ===21.对于两个随机变量V ,W ,若E (V 2),E (W 2)存在,证明:[E (VW )]2≤E (V 2)E (W 2).这一不等式称为柯西许瓦兹(Couchy??Schwarz )不等式. 【证】令2(){[]},.g t E V tW t R =+∈显然22220()[()][2]g t E V tW E V tVW t W ≤=+=++222[]2[][],.E V t E VW t E W t R =++∀∈可见此关于t 的二次式非负,故其判别式Δ≤0, 即2220[2()]4()()E VW E W E V ≥∆=- 2224{[()]()()}.E VW E V E W =-故222[()]()()}.E VW E V E W ≤22.假设一设备开机后无故障工作的时间X 服从参数λ=1/5的指数分布.设备定时开机,出现故障时自动关机,而在无故障的情况下工作2小时便关机.试求该设备每次开机无故障工作的时间Y 的分布函数F (y ).【解】设Y 表示每次开机后无故障的工作时间,由题设知设备首次发生故障的等待时间X ~E (λ),E (X )=1λ=5.依题意Y =min(X ,2). 对于y <0,f (y )=P {Y ≤y }=0. 对于y ≥2,F (y )=P (X ≤y )=1.对于0≤y <2,当x ≥0时,在(0,x )内无故障的概率分布为 P {X ≤x }=1??e ??λx ,所以F (y )=P {Y ≤y }=P {min(X ,2)≤y }=P {X ≤y }=1??e ??y/5.23.已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品.从甲箱中任取3件产品放乙箱后,求:(1)乙箱中次品件数Z 的数学期望;(2)从乙箱中任取一件产品是次品的概率. 【解】(1) Z 的可能取值为0,1,2,3,Z 的概率分布为33336C C {}C k k P Z k -==, 0,1,2,3.k =因此,()0123.202020202E Z =⨯+⨯+⨯+⨯= (2) 设A 表示事件“从乙箱中任取出一件产品是次品”,根据全概率公式有3(){}{|}k P A P Z k P A Z k ====∑191921310.202062062064=⨯+⨯+⨯+⨯= 24.假设由自动线加工的某种零件的内径X (毫米)服从正态分布N (μ,1),内径小于10或大于12为不合格品,其余为合格品.销售每件合格品获利,销售每件不合格品亏损,已知销售利润T (单位:元)与销售零件的内径X 有如下关系T =⎪⎩⎪⎨⎧>-≤≤<-.12,5,1210,20,10,1X X X 若若若 问:平均直径μ取何值时,销售一个零件的平均利润最大【解】(){10}20{1012}5{12}E T P X P X P X =-<+≤≤->{10}20{1012}5{12}(10)20[(12)(10)]5[1(12)]25(12)21(10) 5.P X u u P u X u u P X u u u u u u u u =--<-+-≤-≤--->-=-Φ-+Φ--Φ---Φ-=Φ--Φ--故2/2d ()25(12)(1)21(10)(1)0(()),d x E T u u x u ϕϕϕ-=-⨯---⨯-= 令这里得 22(12)/2(10)/225e 21eu u ----=两边取对数有2211ln 25(12)ln 21(10).22u u --=--解得 125111ln11ln1.1910.91282212u =-=-≈(毫米) 由此可得,当u =毫米时,平均利润最大.25.设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧≤≤.,0,0,2cos 21其他πx x 对X 独立地重复观察4次,用Y 表示观察值大于π/3的次数,求Y 2的数学期望.(2002研考)【解】令 π1,,3(1,2,3,4)π0,3i X Y i ⎧>⎪⎪==⎨⎪≤⎪⎩X .则41~(4,)i i Y Y B p ==∑.因为ππ{}1{}33p P X P X =>=-≤及π/30π11{}cos d 3222x P X x ≤==⎰,所以111(),(),()42,242i i E Y D Y E Y ===⨯=2211()41()()22D YE Y EY =⨯⨯==-,从而222()()[()]12 5.E Y D Y E Y =+=+=26.两台同样的自动记录仪,每台无故障工作的时间T i (i =1,2)服从参数为5的指数分布,首先开动其中一台,当其发生故障时停用而另一台自动开启.试求两台记录仪无故障工作的总时间T =T 1+T 2的概率密度f T (t ),数学期望E (T )及方差D (T ). 【解】由题意知:55e ,0,()0,0t i t f t t -⎧≥=⎨<⎩. 因T 1,T 2独立,所以f T (t )=f 1(t )*f 2(t ).当t <0时,f T (t )=0;当t ≥0时,利用卷积公式得55()5120()()()d 5e 5e d 25e tx t x t T f t f x f t x x x t +∞-----∞=-==⎰⎰故得525e ,0,()0,0.t T t t f t t -⎧≥=⎨<⎩ 由于T i ~E (5),故知E (T i )=15,D (T i )=125(i =1,2)因此,有E (T )=E (T 1+T 2)=25.又因T 1,T 2独立,所以D (T )=D (T 1+T 2)=225. 27.设两个随机变量X ,Y 相互独立,且都服从均值为0,方差为1/2的正态分布,求随机变量|X ??Y |的方差.【解】设Z =X ??Y ,由于22~0,,~0,,22X N Y N ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭且X 和Y 相互独立,故Z ~N (0,1).因22()()(||)[(||)]D X Y D Z E Z E Z -==-22()[()],E Z E Z =-而22/2()()1,(||)||e d 2πz E Z D Z E Z z z +∞--∞===⎰ 2/202e d π2πz z z +∞-== 所以 2(||)1πD X Y -=-. 28.某流水生产线上每个产品不合格的概率为p (0<p <1),各产品合格与否相互独立,当出现一个不合格产品时,即停机检修.设开机后第一次停机时已生产了的产品个数为X ,求E (X )和D (X ).【解】记q =1??p ,X 的概率分布为P {X =i }=q i ??1p ,i =1,2,…,故12111()().1(1)i ii i q p E X iq p p q p q q p ∞∞-=='⎛⎫'===== ⎪--⎝⎭∑∑ 又221211121()()i i i i i i E X i qp i i q p iq p ∞∞∞---=====-+∑∑∑2232211()12112.(1)ii q pq q pq p q p pq q p q p p p∞=''⎛⎫''=+=+⎪-⎝⎭+-=+==-∑所以 22222211()()[()].p pD XE X E X p p p--=-=-=题29图29.设随机变量X 和Y 的联合分布在点(0,1),(1,0)及(1,1)为顶点的三角形区域上服从均匀分布.(如图),试求随机变量U =X +Y 的方差. 【解】D (U )=D (X +Y )=D (X )+D (Y )+2Cov(X ,Y )=D (X )+D (Y )+2[E (XY )??E (X )·E (Y )].由条件知X 和Y 的联合密度为2,(,),(,)0,0.x y G f x y t ∈⎧=⎨<⎩ {(,)|01,01,1}.G x y x y x y =≤≤≤≤+≥ 从而11()(,)d 2d 2.X xf x f x y y y x +∞-∞-===⎰⎰因此11122300031()()d 2d ,()2d ,22X E X xf x x x x E X x x =====⎰⎰⎰22141()()[()].2918D XE X E X =-=-=同理可得 31(),().218E Y D Y ==1115()2d d 2d d ,12xGE XY xy x y x x y y -===⎰⎰⎰⎰541Cov(,)()()(),12936X Y E XY E X E Y =-=-=- 于是 1121()().18183618D U D X Y =+=+-= 30.设随机变量U 在区间[??2,2]上服从均匀分布,随机变量X =1,1,1,1,U U -≤-⎧⎨>-⎩ Y =1,1,1, 1.U U -≤⎧⎨>⎩若 试求(1)X 和Y 的联合概率分布;(2)D (X +Y ).【解】(1) 为求X 和Y 的联合概率分布,就要计算(X ,Y )的4个可能取值(??1,??1),(??1,1),(1,??1)及(1,1)的概率.P {x =??1,Y =??1}=P {U ≤??1,U ≤1} 112d d 1{1}444x x P U ---∞-=≤-===⎰⎰P {X =??1,Y =1}=P {U ≤??1,U >1}=P {∅}=0, P {X =1,Y =??1}=P {U >??1,U ≤1}11d 1{11}44x P U -=-<≤==⎰21d 1{1,1}{1,1}{1}44x P X Y P U U P U ===>->=>=⎰. 故得X 与Y 的联合概率分布为(1,1)(1,1)(1,1)(1,1)(,)~1110424X Y ----⎡⎤⎢⎥⎢⎥⎣⎦. (2) 因22()[()][()]D X Y E X Y E X Y +=+-+,而X +Y 及(X +Y )2的概率分布相应为202~111424X Y -⎡⎤⎢⎥+⎢⎥⎣⎦, 24()~1122X Y ⎡⎤⎢⎥+⎢⎥⎣⎦. 从而11()(2)20,44E X Y +=-⨯+⨯= 211[()]042,22E X Y +=⨯+⨯=所以22()[()][()] 2.D X Y E X Y E X Y +=+-+=31.设随机变量X 的概率密度为f (x )=x-e 21,(??∞<x <+∞)(1) 求E (X )及D (X );(2) 求Cov(X ,|X |),并问X 与|X |是否不相关(3) 问X 与|X |是否相互独立,为什么【解】(1)||1()e d 0.2x E X xx +∞--∞==⎰ 2||201()(0)e d 0e d 2.2x x D X x x x x +∞+∞---∞=-==⎰⎰ (2) Cov(,|)(||)()(||)(||)X X E X X E X E X E X X =-= ||1||e d 0,2x x x x +∞--∞==⎰所以X 与|X |互不相关.(3) 为判断|X |与X 的独立性,需依定义构造适当事件后再作出判断,为此,对定义域??∞<x <+∞中的子区间(0,+∞)上给出任意点x 0,则有0000{}{||}{}.x X x X x X x -<<=<⊂<所以000{||}{} 1.P X x P X x <<<<<故由00000{,||}{||}{||}{}P X x X x P X x P X x P X x <<=<><<得出X 与|X |不相互独立.32.已知随机变量X 和Y 分别服从正态分布N (1,32)和N (0,42),且X 与Y的相关系数ρXY =??1/2,设Z =23YX +.(1) 求Z 的数学期望E (Z )和方差D (Z ); (2) 求X 与Z 的相关系数ρXZ ;(3) 问X 与Z 是否相互独立,为什么 【解】(1) 1().323X Y E Z E ⎛⎫=+=⎪⎝⎭ ()2Cov ,3232XY X Y D Z D D ⎛⎫⎛⎫⎛⎫=++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭11119162Cov(,),9432X Y =⨯+⨯+⨯⨯ 而1Cov(,))()3462XY X Y D Y ρ⎛⎫==-⨯⨯=- ⎪⎝⎭所以 1()146 3.3D Z =+-⨯= (2) 因()()11Cov(,)Cov ,Cov ,Cov ,3232X Y X Z X X X X Y ⎛⎫=+=+ ⎪⎝⎭ 119()(6)3=0,323D X =+⨯-=- 所以 0.)()XZ D Z ρ==(3) 由0XZ ρ==,得X 与Z 不相关.又因1~,3,~(1,9)3Z N X N ⎛⎫ ⎪⎝⎭,所以X 与Z 也相互独立.33.将一枚硬币重复掷n 次,以X 和Y 表示正面向上和反面向上的次数.试求X 和Y 的相关系数XY ρ.【解】由条件知X +Y =n ,则有D (X +Y )=D (n )=0.再由X ~B (n ,p ),Y ~B (n ,q ),且p =q =12, 从而有 ()()4nD X npq D Y ===所以 0()()()2()()XY D X Y D X D Y D X D Y ρ=+=++2,24XY n nρ=+ 故XY ρ=??1. 34. ??1 0 11试求X 和Y 的相关系数ρ.【解】由已知知E (X )=,E (Y )=,而XY 的概率分布为YX ??1 01P所以E (XY )=??+=Cov(X ,Y )=E (XY )??E (X )·E (Y )=??×=0从而 XY ρ=035.对于任意两事件A 和B ,0<P (A )<1,0<P (B )<1,则称ρ=())()()()()()(B P A P B P A P B P A P AB P ⋅-为事件A 和B 的相关系数.试证:(1) 事件A 和B 独立的充分必要条件是ρ=0;(2) |ρ|≤1.【证】(1)由ρ的定义知,ρ=0当且仅当P (AB )??P (A )·P (B )=0.而这恰好是两事件A 、B 独立的定义,即ρ=0是A 和B 独立的充分必要条件. (2) 引入随机变量X 与Y 为1,,0,A X A ⎧⎪=⎨⎪⎩若发生若发生; 1,,0,B Y B ⎧⎪=⎨⎪⎩若发生若发生.由条件知,X 和Y 都服从0??1分布,即01~1()()X P A P A ⎧⎨-⎩ 01~1()()Y P B P B ⎧⎨-⎩从而有E (X )=P (A ),E (Y )=P (B ),D (X )=P (A )·P (A ),D (Y )=P (B )·P (B ),Cov(X ,Y )=P (AB )??P (A )·P (B )所以,事件A 和B 的相关系数就是随机变量X 和Y 的相关系数.于是由二元随机变量相关系数的基本性质可得|ρ|≤1.36. 设随机变量X 的概率密度为Y Xf X (x )=⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<<-.,0,20,41,01,21其他x x令Y =X 2,F (x ,y )为二维随机变量(X ,Y )的分布函数,求: (1) Y 的概率密度f Y (y ); (2) Cov(X ,Y );(3)1(,4)2F -.解: (1) Y 的分布函数为2(){}{}Y F y P Y y P X y =≤=≤.当y ≤0时, ()0Y F y =,()0Y f y =; 当0<y <1时,(){{0}{0Y F y P X P X P X =≤≤=<+≤≤=,()Y f y =;当1≤y <4时,1(){10}{02Y F y P X P X =-≤<+≤≤=()Y f y =;当y ≥4时,()1Y F y =,()0Y f y =. 故Y 的概率密度为1,()04,0,.Y y f y y <<=≤<⎪⎩其他(2) 0210111()()d d d 244+X E X =xf x x x x x x ∞∞=+=⎰⎰⎰--,022********()()()d d d )246+X E Y =E X =x f x x x x x x ∞∞=+=⎰⎰⎰--,02233310117()()()d d d 248+X E XY =E Y =x f x x x x x x ∞∞=+=⎰⎰⎰--,故 Cov(X,Y ) =2()()()3E XY E X E Y =⋅-.(3) 2111(,4){,4}{,4}222F P X Y P X X -=≤-≤=≤-≤11{,22}{2}22P X X P X =≤--≤≤=-≤≤-11{1}24P X =-≤≤-=.37. 设随机变量X 服从参数为1的泊松分布,求P{X=E(X 2)}.解:因为其分布律为P{x=k}=1!e k -,k=0,1,2,…,12211011121111()!(1)!(1)!11(2)!(1)!() 2.k k k k k e k k E X k e e k k k e k k e e e -∞∞∞--===∞∞-==--+===--⎛⎫=+ ⎪--⎝⎭=+=∑∑∑∑∑所以211{()}{2}.2!2P x E X P X e e --=====所以。

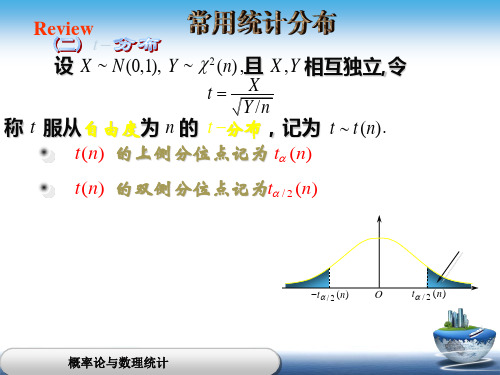
§6.3 统计量及抽样分布6.3.1 统计量为研究一个问题而收集数据,数据就是样本,样本中含有总体的信息。
要实施统计推断,则要依据样本所提供的信息。
样本本身是一堆杂乱无章的数字,需要对这些数字进行加工、整理把样本中所含的信息集中起来以反映总体的各种特征,也就是要由样本计算出一些量以用于统计推断。
这些量是样本的函数而且完全由样本所确定,在统计学中,把凡是由样本算出的量称为统计量。
因此有下面定义。
定义 6.3.1 设n x x x ,..,,21为取自某总体的样本,若样本的函数),...,,(21n x x x T T =中不含任何未知参数,则称T 为统计量。
在此要强调一点:统计量只依赖于样本,而不能与任何未知的量有关,特别地不能依赖于未名参数。
换言之,统计量是能由样本完全确定的量.在具体的统计问题中选用什么统计量,当然要看问题的性质.一个好的统计量应该能很好地集中与问题有关的信息.例如: 样本均值.设n X X X ,...,,21为来自某总体的样本,则样本均值定义为∑==ni i X n X 11若要对总体均值作推断(估计、检验),那么我们很自然地会想到样本均值. 例如: 样本方差.设n X X X ,...,,21为来自某总体的样本,则样本方差定义为212)(11X X n S n i i--=∑= 若要对总体方差作推断(估计、检验),那么我们很自然地会想到样本方差.在这里我们常说“2S 的自由度为1-n ”,自由度这个名词有如下两种解释:(1) 2S 是n 个数X X -1,…,X X n -的平方和,而这n 个数受到一个(也只有一个)约束: ∑==-ni i X X 10)(,故只有1-n 个自由度.(2) 若∑==ni i X n X 11代入21)(X X ni i -∑=中,并将其整理为二次型AX X ',则A 的秩为1-n .自由度就定义为这个秩。
下面列举一些常用的统计量:样本均值: ∑==ni i X n X 11,样本方差: 2111)X -X (-n S ni i 2∑==, 样本标准差:2S S =样本k 阶原点矩:∑==n i k i k X n A 11样本k 阶中心矩:∑==ni k i k )X -(X n B 11样本偏度 2/323ˆB B s =β 样本峰度 3ˆ224-=βB B k次序统计量:设有样本n X ,,X 1,按如下方式定义随机变量)i (X ,当有了样本值n x ,,x 1后,将样本值从小到大排序为)n ((2))x x x ≤≤≤ 1(,那么)i (X 的取值为)i (x ,称i)X (为第i 个次序统计量,称)X X X(n))()2(1,,, (为样本n X ,,X 1的次序统计量, )x x x (n))()2(1,,, (是)X X X (n))()2(1,,, (的一次实现.)(X 1和)n (X 分别称为极小和极大次序统计量. =R )n (X )(X 1-称为样本极差.样本分位数:样本)p p(10<<分位数定义为⎪⎩⎪⎨⎧+=++是整数不是整数,,)p ],[X 21np )1((np 1])np [(n X X m np p 样本中位数为⎪⎪⎩⎪⎪⎨⎧+=++是偶数是奇数,,n X X m n ],[X 21n )12()2n ()21n (5.0 注:样本分位数的定义在不同的教材上可能会有所差异。
样本经验分布函数:对于任意的实数x ,}21{#n ,,,i ,x X )x (V i n =≤=,即)x (V x 表示样本n X ,,X 1中小于或等于x 的频数. 经验分布函数定义为+∞<<-∞=x ,n)x (V )x (F n n . 对应于样本的二重性,统计量也有二重性.若样本n X ,,X 1是n 个随机变量,则统计量)X ,,X (T T n 1=是随机变量. 而对于具体的样本值n x ,,x 1,),,(1n x x T 是一个具体的取值,称此具体取值为统计量的观察值.在统计分析和统计推断中,统计量起着重要作用,对统计量的统计性质的了解就很重要. 比如计算统计量的特征数(比如,期望、方差等),推导统计量的概率分布.例如, 对于任意给定的实数x ,经验分布函数值)(x F n 是一个随机变量,并且)(x nF n 服从二项分布))(,(x F n B ,其中)(x F 为总体分布函数.对于具体的样本观察值n x x ,,1 ,那么经验分布函数)(x F n 的观察值 (经验分布函数)(x F n 的观察值仍记为)(x F n )是一个阶梯形的函数,例如,若样本值n x x ,,1 两两不相等,其次序统计量为)()2()1(,,,n x x x ,则⎪⎪⎩⎪⎪⎨⎧≥-=<≤<=+.,1,1,2,1,,,0,)()()1()()1(n k k n x x n k x x x n kx x x F例6.3.1 设总体X 的数学期望为μ,方差为2σ,n X ,,X 1为来自该总体的简单随机样本,2S ,X 为样本均值和样本方差,则 (1)μ=)X (E(2)n)X (Var 2σ=(3)22σ=)S (E证明:(1)μ===∑∑==ni i n i i )X (E n )X n (E )X (E 1111(2) n)X (Var n )X n (Var )X (Var n i i n i i 212111σ===∑∑==;(3)由于 ∑∑==+=n i i in i i )X X X -X ()X -X (122122∑==ni i X n -X 122,从而∑=n i i )X -X ((E 12)X (nE -)X (E ni i ∑==122221-(n )n /n(-)(n σσμσμ)=++=222 所以 22σ=)S (E例6.3.2 设总体X 的数学期望为μ,方差为2σ,n X ,,X 1为来自该总体的简单随机样本,X 为样本均值.求(1))j i )(X X ,X X Cov(j i ≠--, (2))X X (Var i - 解:(1) j i ≠时)X ,X (Cov )X ,X (Cov )X ,Cov(X )X ,Cov(X )X X ,X X Cov(j i j i j i +--=--222211110σσσσnnnn-=+--=(2) =-)X X (Var i 211σ)n()X X ,X X (Cov i i -=--. 或=-)X X (Var i )X ,X (Cov )X (Var )X Var(i i 2-+211σ)n(-=例 6.3.3 设n X ,,X 1为来自总体))(,(U 00>θθ的简单随机样本,)n (X 为极大次序统计量,求(1))n (X 的概率密度函数;(2))X (E )n (,)X (Var )n (.解:)X ,,X (Max X n )n ( 1=的分布函数为⎪⎪⎩⎪⎪⎨⎧><≤<==θθθx ,,x ,x,x ,)]x (F [x)F n n n M1000( 这里)x (F 是分布),(U θ0的分布函数,从而可得)n (X 的概率密度函数为⎪⎩⎪⎨⎧<<=其他(,,x ,nx x)f n-n M 001θθ 所以 θθθ10+=⋅=⎰n ndx nx x )X (E n1-n )n ( 2n1-n 22)n (2n ndx nx x )X (E θθθ+=⋅=⎰0 )X (Var )n (22221212θθθ)n )(n (n )n n (-n n ++=++=. 例6.3.4 设n X ,,X 1为来自总体X 的简单随机样本,X 的分布函数为)x (F ,)x (F n 为样本的经验分布函数,对于任意给定的实数x ,求(x))(F E n ,(x))F (Var n .解: 对于任意给定的实数x ,)x (V n ~))x (F ,n (B ,从而 (x))(F E n F(x)))x (V (E nn ==1,(x))F (Var n n))x (F -)(x (F ))x (V (Var n n 112==. 6.3.2 抽样分布样本是随机变量,有一定的概率分布。
而统计量是样本的已知函数,那么它是随机变量,有其概率分布,这个分布称为抽样分布。
为特定的统计推断问题而构造特定统计量,由于统计量会受到随机性的影响,因而推断的结果也会有随机性干扰.统计推断方法的优良性只能是从整体效果去考察,而整体效果取决于统计量的抽样分布.因此研究统计量的抽样分布就成为统计推断的一个重要问题.例如, 若n X X X ,...,,21为取自总体),(2σμN 的简单随机样本,用样本均值∑==ni i X n X 11估计总体均值μ,那么这个统计量的抽样分布为),(2n N σμ,从这个抽样分布,我们可以知道样本均值X 是如何围绕总体均值μ而随机波动的,如果σ己知则可以计算出X 与μ的偏差超过一定限度的机会有多大,即概率)|(|ε>μ-X P 。
再比例, 若n X X X ,...,,21为取自总体)(λP 的简单随机样本,那么统计量∑==ni i X T 1的抽样分布为)(λn P 。
如用样本均值∑==ni i X n X 11估计总体均值λ,那么样本均值∑==ni i X n X 11的抽样分布决定了这个估计量的性能。
从原则上讲,统计量的抽样分布可由样本分布定出,但在很多情况下,统计量的精确分布非常复杂. 在统计量的精确分布难以确定或非常复杂时,我们常常求助于统计量的近似分布.例如, 如果n X X X ,...,,21为取自某总体的简单随机样本,总体的均值为μ,方差为2σ。
由中心极限定理知σμ-/)(X n 依分布收敛于)1,0(N ,从而样本均值∑==ni i X n X 11在n 很大时的近似分布为),(2n N σμ.6.3.3 三大分布很多统计推断是基于正态模型(即基于总体为正态分布的假设),而对于来自正态总体的简单随机样本,一些常用统计量(样本均值、样本方差)的精确分布是可以推导出来的.这些分布涉及下面介绍的“三大分布”.(一)2χ分布在第三章中,我们介绍过形状参数为2n,尺度参数为21的Gamma 分布)21,2(n Ga 为自由度为n 的2χ分布.若随机变量n X X X ,...,,21独立同分布于)1,0(N ,那么2i X ~)21,21(Ga ,再由Gamma 分布的可加性知∑=ni i X 12~)21,2(n Ga ,从而∑=ni i X 12服从自由度为n的2χ分布.因此也可以如下方式给出2χ分布的定义.定义5.4.1 设n X X X ,...,,21为取自总体)1,0(N 的简单随机样本,则称统计量∑==χni i X 122的分布为自由度为n 的2χ分布,记为2χ~)(2n χ.由Gamma 分布的概率密度的表达式,易知自由度为n 的2χ分布)(2n χ的密度函数为0,e )2()2/1();(2122>Γ=--x x n x f xnn.自由度为n 的2χ分布)(2n χ的α分位数记为)(2n αχ,即)(2n αχ满足 αχα=>})({2n X P ,其中X ~)(2n χ,分位数)(2n αχ可从附表3中查到.比如31.18)10(205.0=χ.由此定义,易得2χ分布的两条性质:(1) 若随机变量X ~)(2n χ,则n X Var n X E 2)(,)(==.(2) 若随机变量X ~)(2n χ,Y ~)(2m χ,且X 与Y 相互独立,则YX +~)(2m n +χ.例 6.3.5 设n X X X ,...,,21为取自总体),(2σμN 的简单随机样本,则σμ-i X ~),(2σμN (n i ,,2,1 =),从而∑=μ-σni i X 122)(1~)(2n χ.若μ已知,则可得统计量∑=μ-=ni i X T 12)(的密度函数为0,e )2()2/1()(221222>Γ=--t t n t f tn n σσ. (二) t 分布定义 设随机变量1X ~)1,0(N ,2X ~)(2n χ,且1X 与2X 相互独立,则称nX X T /21=的分布为自由度为n 的t 分布,记为t ~)(n t . 自由度为n 的t 分布)(n t 的密度函数为,)(1)2()21();(212+-+Γ+Γ=n n x n n n n x f π+∞<<∞-x .t 分布的密度函数是偶函数,而且随||x 的增大而减少,因此其分布也有标准正态分布类似的特征:中间高,两端低;左右对称.而且有当n ∞→时, 分布)(n t 收敛于标准正态分布)1,0(N . 自由度为n 的t 分布)(n t 的α分位数记为)(n t α,即)(n t α满足 α=>α))((n t t P ,其中t ~)(n t α,分位数)(n t α可从附表4中查到.比如812.1)10(05.0=t .由于t 分布的密度函数是偶函数,故分位数有如下关系)(n t α0)(1=+α-n t ,当自由度较大(如30≥n )时, t 分布可用标准正态分布)1,0(N 近似, t 分布的分位数可用标准正态分布)1,0(N 的分位数近似.t 分布的性质:(1) 1>n 时, 分布)(n t 的数学期望存在,且期望为0. (2) 2>n 时, 分布)(n t 的方差存在,且方差为2-n n . (3) 若t ~)(n t ,则2t ~),1(n F .例 6.3.6 设n X X X ,...,,21为取自总体),0(2σN 的简单随机样本,则~)1(-n t .(三) F 分布定义 设随机变量1X ~)(2m χ,2X ~)(2n χ,且1X 与2X 相互独立, 称nX mX F //21=的分布为自由度为m 和n 的F 分布,记为F ~),(n m F . 自由度为m 和n 的F 分布),(n m F 的密度函数为0,)n m (1)2()2()/)(2(),;(2122>+ΓΓ+Γ=+--x x x n m n m nm m n x f n m m m自由度为m 和n 的F 分布),(n m F 的α分位数记为),(n m F α,即),(n m F α满足α=>α)),((n m F F P ,其中F ~),(n m F α,分位数),(n m F α可从附表5中查到.比如74.4)5,10(05.0=F .由此定义,易得F 分布的性质: (1) 若随机变量F ~),(n m F ,则F1~),(m n F . (2)),(1),(1m n F n m F αα-=.例 6.3.7 设n X X X ,...,,21为取自总体),(2σμN 的简单随机样本,则))(/()()(1212∑∑+==μ-μ--nk i iki i XkX k n ~),(k n k F -.例 6.3.8 设m X X X ,...,,21为取自总体),(211σμN 的简单随机样本, 设n Y Y Y ,...,,21为取自总体),(222σμN 的简单随机样本,且两样本独立,则∑∑==σμ-σμ-ni i mi i Y m X n 1222212121/)(/)(~),(n m F .6.3.4 正态总体的抽样分布在正态总体下,样本均值和样本方差等常用统计量的精确分布是可以导出的.下面给出其结果.定理6.3.1 设n X ,,X 1为来自总体),N(2σμ的简单随机样本,2S ,X 为样本均值和样本方差,则 (1)X ~/n),N(2σμ,(2)221σS)-n (212σ∑==ni i)X -X(~)-n (12χ,(3)2S ,X 相互独立.对于结论(1),利用正态分布的性质易得,下面给出结论(2),(3)的证明.证明:记=X ),,(1'n X X L ,则X ~),1(2n I N σμ,其中)1,...,1,1(1'=,n I 为n 阶单位矩阵。