金属自由气体模型
- 格式:doc
- 大小:1.89 MB
- 文档页数:24


固体物理基础习题解答第一章 金属自由电子气体模型思 考 题1.如何理解电子分布函数)(E f 的物理意义是: 能量为E 的一个量子态被电子所占据的平均几率?[解答]金属中的价电子遵从费密-狄拉克统计分布, 温度为T 时, 分布在能级E 上的电子数目1/)(+=-T k E E B F e g n ,g 为简并度, 即能级E 包含的量子态数目. 显然, 电子分布函数11)(/)(+=-T k E E B F e E f是温度T 时, 能级E 的一个量子态上平均分布的电子数。
因为一个量子态最多由一个电子所占据, 所以)(E f 的物理意义又可表述为: 能量为E 的一个量子态被电子所占据的平均几率。
2.绝对零度时, 价电子与晶格是否交换能量?[解答]晶格的振动形成格波,价电子与晶格交换能量,实际是价电子与格波交换能量。
格波的能量子称为声子, 价电子与格波交换能量可视为价电子与声子交换能量。
频率为i ω的格波的声子数11/-=T k i B i e n ω .从上式可以看出, 绝对零度时, 任何频率的格波的声子全都消失。
因此, 绝对零度时, 价电子与晶格不再交换能量.3.你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的?[解答]自由电子论只考虑电子的动能. 在绝对零度时, 金属中的自由(价)电子, 分布在费密能级及其以下的能级上, 即分布在一个费密球内。
在常温下, 费密球内部离费密面远的状态全被电子占据, 这些电子从格波获取的能量不足以使其跃迁到费密面附近或以外的空状态上, 能够发生能态跃迁的仅是费密面附近的少数电子, 而绝大多数电子的能态不会改变。
也就是说, 常温下电子的平均动能与绝对零度时的平均动能一定十分相近。
4.晶体膨胀时, 费密能级如何变化?[解答] 费密能级3/2220)3(2πn m E F=,其中n 是单位体积内的价电子数目. 晶体膨胀时, 体积变大, 电子数目不变, n 变小, 费密能级降低. 5.为什么温度升高, 费密能反而降低?[解答]当0≠T 时, 有一半量子态被电子所占据的能级即是费密能级. 温度升高, 费密面附近的电子从格波获取的能量就越大, 跃迁到费密面以外的电子就越多, 原来有一半量子态被电子所占据的能级上的电子就少于一半, 有一半量子态被电子所占据的能级必定降低. 也就是说, 温度升高, 费密能反而降低. 6.为什么价电子的浓度越大, 价电子的平均动能就越大?[解答]由于绝对零度时和常温下电子的平均动能十分相近,我们讨论绝对零度时电子的平均动能与电子浓度的关系.价电子的浓度越大价电子的平均动能就越大, 这是金属中的价电子遵从费密—狄拉克统计分布的必然结果. 在绝对零度时, 电子不可能都处于最低能级上, 而是在费密球中均匀分布。





D r u d e 模型一. Drude 模型的提出1897年在研究放电管辉光放电实验中的阴极射线时,Thomson 是通过将组成阴极射线的电子当作经典粒子而最先发现了电子的存在。
在发现电子后的最初一段时期内,对原子结构的研究尚处于探索之中,还没有认识到电子等微观粒子运动的独特本质。
因此,在当时还不具备解释金属中的这些传导电子是如何形成以及怎么运动这两个基本问题的理论基础。
1900年受气体分子运动论的启发提出了金属中经典的自由电子理论即Drude 模型,即认为金属中存在有自由电子气体,并用这一理论来解释金属材料的导电、导热等宏观性能。
二. Drude 模型的四个基本假设1.独立电子近似近似认为电子的运动是彼此独立的,就象孤立的单个电子一样,故又称为单电子近似。
2.自由电子近似用经典粒子的碰撞图象来简化电子与离子实之间复杂的相互作用近似认为单个电子在与离子实的相继两次碰撞之间作自由运动,故金属中的传导电子又常称为自由电子3.弛豫时间近似在dt 时间内电子与离子实之间碰撞的几率应为dt/τ。
电子在单位时间内碰撞一次的几率为1/τ,τ称为弛豫时间(即平均自由时间)。
每次碰撞时,电子失去它在电场作用下获得的能量,即电子和周围环境达到热平衡仅仅是通过与原子实的碰撞实现的。
4.经典近似在与离子实的相继两次碰撞之间电子的运动遵循Newton 运动定律碰撞前后电子遵循Boltzmann 统计分布。
三.Drude 模型的成就自由电子气体+波尔兹曼统计欧姆定律○虽然金属至少有两种带电粒子,离子与电子,Drude 假设参与导电作用的仅是其中一种。
○传导电子的来源:价电子与芯电子。
◎首先,来解释金属的导电现象并导出电导率。
电子:平均速度为经典近似假设:热运动遵循Maxwell 速度分布律,故有 ◎若与离子实相继两次碰撞之间的时间间隔为t ,则有 因此有 表明:在外电场作用下金属中的自由电子将形成与外电场方向相反的宏观定向运动,于是就形成了电流◎由此可得到金属材料电导率的微观表达式四.Drude 模型的不足以电子的平均自由程为例,来说明Drude 电子模型所遇到的根本性困难。

金属自由电子气理论特鲁德电子气模型:特鲁德提出了第一个固体微观理论利用微观概念计算宏观实验观测量自由电子气+波尔兹曼统计→欧姆定律 电子平均自由程+分子运动论→电子的热导率特鲁德(Paul Drude )模型的基本假设11.自由电子近似:传导电子由原子的价电子提供,离子实对电子的作用可以忽略不计,离子实的作用维持整个金属晶体的电中性,与电子发生碰撞。
2.独立电子近似:电子与电子之间的相互作用可以忽略不计。
外电场为零时,忽略电子之间的碰撞,两次碰撞(与离子实碰撞)之间电子自由飞行(与经典气体模型不同,电子之间没有碰撞,电子只与离子实发生碰撞,这一点我们将在能带论中证明是错误的。
)特鲁德(Paul Drude )模型的基本假设23.玻尔兹曼统计:自由电子服从玻尔兹曼统计。
4.弛豫时间近似:电子在单位时间内碰撞一次的几率为1/τ,τ称为弛豫时间(即平均自由时间)。
每次碰撞时,电子失去它在电场作用下获得的能量,即电子和周围环境达到热平衡仅仅是通过与原子实的碰撞实现的。
特鲁德模型的成功之处——成功解释了欧姆定律欧姆定律E j ρ=(或j E σ=),其中E 为外加电场强度、ρ为电阻率、j 为电流密度。
202()1I j nev ne S j E eEt m v v E j m ne eE m v m τρτστρ⎧==-⎪⎧=⎪⎪-⎪⎪=+⇒⇒=⎨⎨⎪⎪==⎪⎪⎩=-⎪⎩2.经典模型的另一困难:传导电子的热容根据理想气体模型,一个自由粒子的平均热量为3/2B k T ,故333(),222A B e U U N k T RT C R T ∂====∂33/29v ph e C C C R R =+=+≈(卡/molK.)但金属在高温时实验值只有6(卡/molK.),即3v C R ≈。
4.2 Sommerfeld 的自由电子论1925年:泡利不相容原理 1926年:费米—狄拉克量子统计 1927年:索末菲半经典电子论抛弃了特鲁德模型中的玻尔兹曼统计,认为电子气服从费米—狄拉克量子统计得出了费米能级,费米面等重要概念,并成功地解决了电子比热比经典值小等经典模型所无法解释的问题。


金属中的自由电子模型在金属中,原子固定在晶格中,共享其外层电子形成金属键。
与共价键不同,金属键不是由两个原子共享电子形成的,而是由整个金属晶体共享所有电子形成的。
因此,金属中的电子是高度移动的,可以在整个晶体中自由移动。
这种高度移动的电子被称为自由电子。
自由电子模型为了更好地理解金属中的自由电子,我们可以使用自由电子模型来进行说明。
自由电子模型假设金属中的所有原子共享它们的外层电子,形成一个巨大的电子气体。
这个电子气体中的电子可以看作是独立的,它们可以在整个晶体中自由移动,没有受到单个原子的束缚。
这种自由运动的电子是金属的导电电子,可以在金属中形成电流。
自由电子模型的一个重要假设是,电子在金属中形成一个连续的能带。
这个能带可以看作是一系列接近的能级,电子可以在其中自由移动。
不同的金属有不同的能带结构,这决定了它们的导电性和其他电学和热学性质。
在自由电子模型中,金属晶体的离子核可以看作是一个均匀的正电荷背景,与电子相互作用形成电子-正离子相互作用。
这种相互作用决定了自由电子的运动和能带结构。
能带结构能带结构是自由电子模型的一个重要概念。
在一个金属晶体中,由于相邻的原子之间形成了化学键,形成了共享电子的状态。
在这种情况下,电子的能量不再被离子核所束缚,而是自由移动。
它们可以在一系列接近的能级上自由移动,形成了能带结构。
概念上,我们可以将能带结构看作单位晶体内的所有电子的哈密顿量,哈密顿量代表所有电子的能量。
根据能带结构理论,所有电子都会填充到有限数量的能带中。
当一个能带被填充满时,下一个更高的能带就变成了空的,这个空的能带就可以被其他电子占据,从而继续导电。
导电性金属的导电性可以通过自由电子模型来解释。
在自由电子模型中,金属中的电子可以以任何方向自由移动,导致电流。
金属中的导电性与其能带结构有关。
金属中的电子被分为价带和导带,价带电子被紧密束缚在原子周围的状态中,电子的运动受到离子核的束缚。
而导带电子则在能带结构中自由移动,不受到束缚。
2023年固体物理基础第三版(阎守胜著)课后题答案下载固体物理基础第三版(阎守胜著)课后答案下载第一章金属自由电子气体模型1.1 模型及基态性质1.1.1 单电子本征态和本征能量1.1.2 基态和基态的能量1.2 自由电子气体的热性质1.2.1 化学势随温度的变化1.2.2 电子比热1.3 泡利顺磁性1.4 电场中的`自由电子1.4.1 准经典模型1.4.2 电子的动力学方程1.4.3 金属的电导率1.5 光学性质1.6 霍尔效应和磁阻1.7 金属的热导率1.8 自由电子气体模型的局限性第二章晶体的结构2.1 晶格2.1.1 布拉维格子2.1.2 原胞2.1.3 配位数2.1.4 几个常见的布拉维格子2.1.5 晶向、晶面和基元的坐标2.2 对称性和布拉维格子的分类2.2.1 点群2.2.2 7个晶系2.2.3 空间群和14个布拉维格子2.2.4 单胞或惯用单胞2.2.5 二维情形2.2.6 点群对称性和晶体的物理性质 2.3 几种常见的晶体结构2.3.1 CsCl结构和立方钙钛矿结构 2.3.2 NaCl和CaF、2结构2.3.3 金刚石和闪锌矿结构2.3.4 六角密堆积结构2.3.5 实例,正交相YBa2Cu307-82.3.6 简单晶格和复式晶格2.4 倒格子2.4.1 概念的引入2.4.2 倒格子是倒易空间中的布拉维格子 2.4.3 倒格矢与晶面2.4.4 倒格子的点群对称性2.5 晶体结构的实验确定2.5.1 X射线衍射2.5.2 电子衍射和中子衍射2.5.3 扫描隧穿显微镜第三章能带论I3.1 布洛赫定理及能带3.1.1 布洛赫定理及证明3.1.2 波矢七的取值与物理意义3.1.3 能带及其图示3.2 弱周期势近似3.2.1 一维情形3.2.2 能隙和布拉格反射3.2.3 复式晶格3.3 紧束缚近似3.3.1 模型及计算3.3.2 万尼尔函数3.4 能带结构的计算3.4.1 近似方法3.4.2 n(K)的对称性3.4.3 n(K)和n的图示3.5 费米面和态密度3.5.1 高布里渊区3.5.2 费米面的构造3.5.3 态密度第四章能带论Ⅱ4.1 电子运动的半经典模型 4.1.1 模型的表述4.1.2 模型合理性的说明4.1.3 有效质量4.1.4 半经典模型的适用范围4.2 恒定电场、磁场作用下电子的运动4.2.1 恒定电场作用下的电子4.2.2 满带不导电4.2.3 近满带中的空穴4.2.4 导体、半导体和绝缘体的能带论解释 4.2.5 恒定磁场作用下电子的准经典运动 4.3 费米面的测量4.3.1 均匀磁场中的自由电子4.3.2 布洛赫电子的轨道量子化4.3.3 德哈斯一范阿尔芬效应4.3.4 回旋共振方法4.4 用光电子谱研究能带结构4.4.1 态密度分布曲线4.4.2 角分辨光电子谱测定n(K)4.5 一些金属元素的能带结构4.5.1 简单金属4.5.2 一价贵金属4.5.3 四价金属和半金属4.5.4 过渡族金属和稀土金属第五章晶格振动5.1 简谐晶体的经典运动5.1.1 简谐近似5.1.2 一维单原子链,声学支 5.1.3 一维双原子链,光学支 5.1.4 三维情形5.2 简谐晶体的量子理论5.2.1 简正坐标5.2.2 声子5.2.3 晶格比热5.2.4 声子态密度5.3 晶格振动谱的实验测定 5.3.1 中子的非弹性散射5.3.2 可见光的非弹性散射 5.4 非简谐效应5.4.1 热膨胀5.4.2 晶格热导率第六章输运现象6.1 玻尔兹曼方程6.2 电导率6.2.1 金属的直流电导率6.2.2 电子和声子的相互作用 6.2.3 电阻率随温度的变化 6.2.4 剩余电阻率6.2.5 近藤效应06.2.6 半导体的电导率6.3 热导率和热电势6.3.1 热导率6.3.2 热电势6.4 霍尔系数和磁阻第七章固体中的原子键合7.1 概述7.1.1 化学键7.1.2 晶体的分类7.1.3 晶体的结合能7.2 共价晶体7.3 离子晶体7.3.1 结合能7.3.2 离子半径7.3.3 部分离子部分共价的晶体7.4 分子晶体、金属及氢键晶体7.4.1 分子晶体7.4.2 量子晶体7.4.3 金属……第八章缺陷第九章无序第十章尺寸第十一章维度第十二章关联固体物理基础第三版(阎守胜著):基本信息阎守胜,1938生出生,1962年毕业于北京大学物理系,现任北京大学物理学院教授,博士生导师,兼任中国物理学会《物理》杂志主编,他长期从事低温物理,低温物理实验技术,高温超导电性物理和介观物理方面的实验研究,并讲授大学生的固体物理学,低温物理学和现代固体物理学等课程。
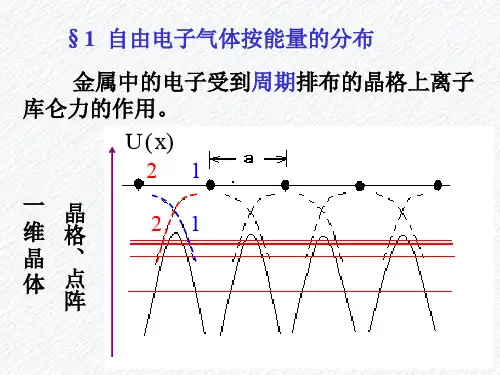
第十九讲金属自由气体模型一、固体物理中的主要模型(理论):Atoms in the solid matter= ion cores (离子实)+ valence electrons(价电子)= nuclei + core electrons + valence electrons1.最简单的模型—金属自由电子气体模型a)认为离子实静止不动;b)通过“自由电子近似(凝胶模型--离子实系统产生的势场是均匀的)”和“独立电子近似(忽略电子与电子之间的作用)”形成一类最简单的“单电子近似”模型:i.Drude Model (1900)ii.Sommerfeld Model (1928)2.次简单模型Ⅰ—晶格模型和能带理论a)认为离子实仍然静止不动;b)离子实系统产生的势场随空间是周期变化,不再是均匀的。
3.次简单模型Ⅱ—晶格振动理论和声子模型a)不考虑电子的运动;b)离子以简正模式运动。
4.最复杂的模型—电子与声子相互作用理论,光子与声子相互作用理论,光子与电子(固体、半导体中的电子,)相互作用理论,…总结:学习这种将复杂的大问题(真实的物理体系)化成可以局部求解的小问题(简化的物理体系);通过不断对简单模型的修正,来处理复杂的体系。
在学会这种思维方式的同时,保持头脑清醒,牢记各种模型的成立前提(或条件,或可忽略的物理内容),才能正确使用模型,得到合理的有价值的结论。
二、Sommerfeld量子金属自由电子气体模型通过三个近似,将一块体积为V的金属简单地看成一堆价电子在体积为V的“空盒子”中运动的单纯由电子组成的体系。
1.自由电子近似——对金属来说是个比较好的近似。
a)忽略价电子与离子实之间的作用,认为离子实系统产生的势场对处在其中的价电子来说是均匀的。
b)将离子实系统看成是保持体系电中性的均匀正电荷背景。
c)价电子的自由运动范围仅限于金属块的体积V内,由金属的表面势垒将价电子限制在样品内部。
2.独立电子近似——对其它晶体(包括半导体和绝缘体)来说也是一个比较好的近似。
a)忽略价电子与电子之间的作用,把其它电子对某一个价电子的作用看成是平均场;b) 认为某一个价电子的运动不影响其他电子的运动;c) 把多价电子问题转换成单电子问题求解单电子能量本征态。
d) 最后让多个价电子按照一些规则(能量最小原理(T=0),费米分布(T>0),泡利不相容原理)来填充单电子能量本征态。
e) 多个价电子填充单电子能量本征态的规则:1. 泡利不相容原理2. 能量最小原理(T=0)3. 费米分布(T>0)3. 弛豫电子近似——在考虑电子输运过程中,不能忽略电子与电子之间的作用,加入一个唯象的近似假设a) 在有外场(电场,磁场,电磁波场和光)作用时对价电子体系采取的一种近似;b) 认为每一个价电子会受到散射和碰撞(由于其他电子的存在与运动)。
三、金属自由电子气体密度3:n n cm ⎡⎤⎢⎥⎣⎦单质金属晶体原子密度3:N N cm ⎡⎤⎢⎥⎣⎦,比重/质量密度(density )3g cm ρ⎡⎤⎢⎥⎣⎦,原子量(atomic mass)g A mol ⎡⎤⎢⎥⎣⎦, 阿佛加德罗常数236.02210A N mol =⨯,Z 每个原子的价电子个数。
3A AZ N n ZN Zcm A A N ρρ⎡⎤===⎢⎥⎣⎦ 金属自由电子气体密度n 典型值为222331010cm :,比理想气体密度大1000倍。
Condensed gas四、金属自由电子模型中单电子能量本征态和能量本征值目的:求金属自由电子气体的能量密度3:J cm ε⎡⎤⎢⎥⎣⎦。
由独立电子近似,金属中每一个价电子是相互独立的,有相同的运动规律;每个电子都有自己的能量本征态,只要求出单个电子的能量本征态,再复制n 套,在把价电子填充在这些能量本征态上,就可以得到n 个电子的总能量,即金属自由电子气体的能量密度3:J cm ε⎡⎤⎢⎥⎣⎦。
T. YANG Page 5 of 24 6/30/2019波函数归一化和k r矢量意义:T. YANG Page 6 of 24 6/30/2019周期边界条件和k r矢量取值:Periodic boundary conditions1) Surface is not important.2) Useful for large N (bulk solids N ≈ 1023/cm 3). 3) Similar procedure; slightly different results.--------…………--T. YANG Page 7 of 24 6/30/2019T. YANG Page 8 of 24 6/30/2019k r 空间(倒空间):把波矢k r 看成空间矢量,在直角坐标系中用k r 矢量的末端的位置表示每一个允许的k r 值。
这个直角坐标系所在的空间叫做k r空间(或倒空间)k r 空间(或倒空间)中一个点占据的k r空间(或倒空间)的体积为()()3333222L L V πππ⎛⎫==⎪⎝⎭。
定义态密度:单位k r 空间体积内包含电子态的个数(k r 点的个数)称为k r空间的态密度()()33122Vf Vππ==。
单电子本征能量及单电子态在k r空间(或倒空间)中的能级图1. 等能面是球面2.抛物面(抛物线)能带五、金属自由电子气体基态能量本征态和基态能量本征值T= 0 K,N个价电子所处的状态为基态。
The ground state (T=0) of a system of fermions is governed by the Pauli Exclusion Principle: all the low-energy states are filled to a certain maximum energy E F which depends on the density of the fermionic “gas” (the so-called Fermi energy).N free electrons at T=0 K,()()2222/321/321/3323322432383FF F F F FV N N k k n V k k E n m mv mπππππ⎛⎫=⋅⋅⇒== ⎪⎝=⎭==h h hThe average thermal velocity for ideal gas depend on temperature, T ,k B T ~ 0.026 eV21322e B m v k TWhen we consider ensembles of identical particles , we need to distinguish two regimes: the low-density limit (the inter-particle distance is much greater than the de Broglie wavelength of these particles) and the high-density limit (the opposite is true). In the low-density limit, bosonic and fermionic ensembles behave in a similar way (Boltzmann statistics). In the high-density limit, fermions and bosons are quite different!high-density limitOccupancy (= the distribution function): the mean number of fermions in a particular quantum staten=N/V – the average density of particles()31C dB n n λ≥∝()01,0,F FD T FE f E εεε=≤⎧=⎨>⎩()()f n εε≡()if E n=∑3D Cubic Infinite Potential Well•1-D Well•3-D “Cubic” Well (with sides length L)三维各向同性“立方盒子”的能级简并度d(Degeneracy for an Energy Level),34 Electrons in 3D Infinite Well34 Electrons in 3D Infinite Well•In this configuration, Array–What is the probability at T =0 that a level with energy 14E0 or less will be occupied?–It is 1!–What is the probability that the level withenergy above 14E0 will be occupied?–It is 0!Pauli Exclusion Principle●How do we extend the quantum theory to systemsbeyond the hydrogen atom?●For systems of 2 electrons, we simply have a ψ thatdepends on time and the coordinates of each of the two electrons:●ψ(x1,y1,z1,x2,y2,z2,t)●and the Schrodinger’s equation has two kineticenergies instead of one.●It turns out that the Schodinger’s Equation can beseparated:T. YANG Page 17 of 24 6/30/2019●ψ = X a(x1,y1,z1) * X b(x2,y2,z2) * T(t) .●This is like having electron one in state a, and having electron two in state b. Note that eachstate has its own particular set of quantum numbers.●However, from the Heisenberg Uncertainty Principle (from wave/particle duality), we are notreally sure which electron is electron number #1 and which is number #2. This means that the wavefunction must also reflect this uncertainty.●There are two ways of making the wavefunction reflect the indistinguishability of the twoelectrons:ψsym = [X a(r1)*X b(r2) + X b(r1)*X a(r2) ]* T(t)andψanti = [X a(r1)*X b(r2) - X b(r1)*X a(r2) ]* T(t) .●Which (if either) possibility agrees with experiment?●It turns out that some particles are explained nicely by the symmetric, and some are explainedby the antisymmetric.●Those particles that work with the symmetric form are called BOSONS. All of theseparticles have integer spin as well. Note that if boson 1 and boson 2 both have the same state, ψ > 0. This means that both particles CAN be in the same state at the same location at the same time.●Those particles that work with the anti-symmetric wavefunction are called FERMIONS. Allof these particles have half-integer spin. Note that if fermion 1 and fermion 2 both have the same state, ψ= 0. This means that both particles can NOT be in the same state at the same location at the same time.T. YANG Page 18 of 24 6/30/2019●FERMIONS. Electrons, protons and neutrons are fermions. These particles can NOT bein the same location with the same energy state at the same time.●This means that two electrons going around the same nucleus can NOT both be in theexact same state at the same time!This is known as the Pauli Exclusion Principle!●BOSONS. Photons and alpha particles(2 neutrons + 2 protons) are bosons. Theseparticles can be in the same location with the same energy state at the same time.●This occurs in a laser beam, where all the photons are at the same energy (monochromatic). Electron SpinT. YANG Page 19 of 24 6/30/2019T. YANGPage 20 of 246/30/20192Im()sin 11sin nlm nlm nlm r m j e r e e e r r r ϕθϕϕμμθθθϕ*=ψ∇ψ=ψ∂∂∂∇=++∂∂∂r rhh r r r 222222200222000sin (sin )sin (sin )sin sin 22e nlm e L Z Z nlm ZL Z Z nlm Znlm L Z Zem j e r d e rd dr e dI j d e em d e S dI e r rd dr e r em e e r rd drr em e d r d drem e e ϕϕϕϕπππμθσθσμπθθμθμπθθμθϕθθμμμ∞∞=-ψ=⋅=⋅=⋅=-ψ⋅=-ψ⋅=-ψ⋅=-⎰⎰⎰⎰⎰r r h r r r r r r r h r r h r h r r h2222Z L Z Zz L Z Z L zL em e e eL e e e L e Lμμμμμμμμ=-=-=-=-r r h r r v vT. YANG,,2(,)()()()alkai atom n l l s l R E E E hcT n l r L S hc r L S n ξξ-=+∆=-+⋅=-+⋅-∆r r v v),,,,(),,,,(j s l m j s l n m s m l nThe other kinds of micro-particles:The properties of proton : s=1/2, c=+e, m=m p The properties of neutron : s=1/2, c=0, m=m n The properties of photon : s=1, c=0, m=0The properties of electron : s=1/2, c=-e, m=m eT>0 K 自由电子气体能量的计算The DoS for a 3D free electron gas (m is the electron mass) : n, l, m l , s, m ss=1/2 :spinm s =+1/2,- 1/2 :spin magneticm l =0,±1, ±2, …,±l :magneticl=0,1, 2, …,n-1 :orbitaln=1, 2, … :principal()3/231/222122D m g εεπ⎛⎫= ⎪⎝⎭h。