金属自由电子气理论

一,金属自由电子气体模型1.1 经典电子论特鲁德电子气模型：特鲁德提出了第一个固体微观理论利用微观概念计算宏观实验观测量自由电子气+波尔兹曼统计→欧姆定律电子平均自由程+分子运动论→电子的热导率特鲁德（Paul Drude ）模型的基本假设11.自由电子近似：传导电子由原子的价电子提供，离子实对电子的作用可以忽略不计，离子实的作用维持整个金属晶体的电中性，与电子发生碰撞。

2.独立电子近似：电子与电子之间的相互作用可以忽略不计。

外电场为零时，忽略电子之间的碰撞，两次碰撞（与离子实碰撞）之间电子自由飞行（与经典气体模型不同，电子之间没有碰撞，电子只与离子实发生碰撞，这一点我们将在能带论中证明是错误的。

）特鲁德（Paul Drude ）模型的基本假设23.玻尔兹曼统计：自由电子服从玻尔兹曼统计。

4.弛豫时间近似：电子在单位时间内碰撞一次的几率为1/τ，τ称为弛豫时间（即平均自由时间）。

每次碰撞时，电子失去它在电场作用下获得的能量，即电子和周围环境达到热平衡仅仅是通过与原子实的碰撞实现的。

特鲁德模型的成功之处——成功解释了欧姆定律欧姆定律E j ρ=（或j E σ=），其中E 为外加电场强度、ρ为电阻率、j 为电流密度。

202()1I j nev ne Sj E eEt m v v E j m ne eE m v m τρτστρ⎧==-⎪⎧=⎪⎪-⎪⎪=+⇒⇒=⎨⎨⎪⎪==⎪⎪⎩=-⎪⎩r1.2.经典模型的另一困难：传导电子的热容根据理想气体模型，一个自由粒子的平均热量为3/2B k T ，故333(),222A B e U U N k T RT C R T ∂====∂33/29v ph e C C C R R =+=+≈（卡/molK.）但金属在高温时实验值只有6（卡/molK.），即3v C R ≈。

1.3 Sommerfeld 的自由电子论1925年：泡利不相容原理1926年：费米—狄拉克量子统计 1927年：索末菲半经典电子论抛弃了特鲁德模型中的玻尔兹曼统计，认为电子气服从费米—狄拉克量子统计得出了费米能级，费米面等重要概念，并成功地解决了电子比热比经典值小等经典模型所无法解释的问题。

金属自由电子气理论特鲁德电子气模型：特鲁德提出了第一个固体微观理论利用微观概念计算宏观实验观测量自由电子气+波尔兹曼统计→欧姆定律 电子平均自由程+分子运动论→电子的热导率特鲁德（Paul Drude ）模型的基本假设11.自由电子近似：传导电子由原子的价电子提供，离子实对电子的作用可以忽略不计，离子实的作用维持整个金属晶体的电中性，与电子发生碰撞。

2.独立电子近似：电子与电子之间的相互作用可以忽略不计。

外电场为零时，忽略电子之间的碰撞，两次碰撞（与离子实碰撞）之间电子自由飞行（与经典气体模型不同，电子之间没有碰撞，电子只与离子实发生碰撞，这一点我们将在能带论中证明是错误的。

）特鲁德（Paul Drude ）模型的基本假设23.玻尔兹曼统计：自由电子服从玻尔兹曼统计。

4.弛豫时间近似：电子在单位时间内碰撞一次的几率为1/τ，τ称为弛豫时间（即平均自由时间）。

每次碰撞时，电子失去它在电场作用下获得的能量，即电子和周围环境达到热平衡仅仅是通过与原子实的碰撞实现的。

特鲁德模型的成功之处——成功解释了欧姆定律欧姆定律E j ρ=（或j E σ=），其中E 为外加电场强度、ρ为电阻率、j 为电流密度。

202()1I j nev ne S j E eEt m v v E j m ne eE m v m τρτστρ⎧==-⎪⎧=⎪⎪-⎪⎪=+⇒⇒=⎨⎨⎪⎪==⎪⎪⎩=-⎪⎩2.经典模型的另一困难：传导电子的热容根据理想气体模型，一个自由粒子的平均热量为3/2B k T ，故333(),222A B e U U N k T RT C R T ∂====∂33/29v ph e C C C R R =+=+≈（卡/molK.）但金属在高温时实验值只有6（卡/molK.），即3v C R ≈。

4.2 Sommerfeld 的自由电子论1925年：泡利不相容原理 1926年：费米—狄拉克量子统计 1927年：索末菲半经典电子论抛弃了特鲁德模型中的玻尔兹曼统计，认为电子气服从费米—狄拉克量子统计得出了费米能级，费米面等重要概念，并成功地解决了电子比热比经典值小等经典模型所无法解释的问题。

金属导电的微观解释涉及到金属的电子结构和电子运动。

金属的导电性质主要归因于其特殊的电子排布和电子运动方式。

1. 自由电子模型：金属的电子结构可以通过自由电子模型来描述。

在金属晶格中，金属原子的外层电子几乎是自由移动的，形成了被称为“电子海”的电子云。

这些自由电子不受特定原子核束缚，可以在整个金属结构中自由移动。

2. 电子的漂移：当外部电场施加在金属上时，自由电子将受到电场的作用力。

根据牛顿的第二定律，受力的电子将产生加速度。

然而，由于金属中电子的质量非常小，所以在实际情况下，电子受到的阻尼较小，加速度较大。

3. 电子的碰撞：自由电子在金属晶格中会与金属离子和其他自由电子发生碰撞。

这些碰撞会导致电子的散射，但由于电子海中有大量自由电子，导致整体上电流的流动方向保持不变。

4. 导电性的来源：由于自由电子的高度流动性，它们可以在电场作用下形成电流。

这就是金属的导电性质的基本来源。

而金属晶格中的离子网络对电子的碰撞提供了一些阻力，但这种阻力相对较小，不会阻止电流的形成。

综合来看，金属导电的微观解释可以概括为：在金属中，存在大量自由移动的电子，它们受到外部电场的作用，形成电流，而金属晶格中的离子提供了一些散射阻力，但整体上电子仍能在金属中自由传导，从而表现出良好的导电性。

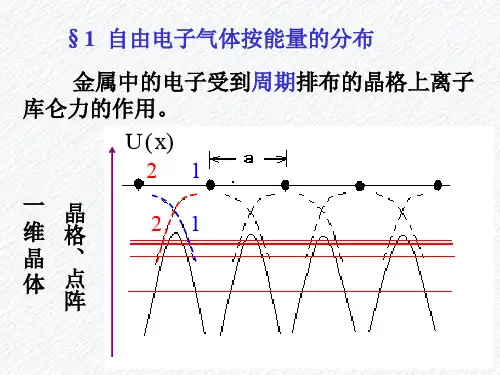
第六章金属电子论主要内容：金属自由电子气的量子理论●电子气的能量状态●费米－狄拉克统计●电子气的热容量●金属电导率、功函数、热电子发射金属电导和热导的宏观规律●欧姆定律（1821年）:●维德曼－弗兰茨定律（1853年）在不太低的温度下，金属的热导率和电导率的之比正比于温度，其比例常数的值不依赖于具体的金属（该常数称为洛伦茨常数）6.1自由电子气的量子理论金属由两部分构成：●位于晶格的离子实（ion core，由原子核和内层电子构成，在形成晶体时，离子实的变化可以忽略）●价电子（valence electron），价电子游历于固定的离子实周围，弥散于金属内部的全部空间，构成自由电子气（electron gas）自由电子气模型的基本假定：①独立电子假设：忽略电子与电子之间的库仑排斥相互作用。

②自由电子假设：忽略电子和离子之间库仑吸引相互作用。

③金属中传导电子是服从量子力学规律费米子，其能态由薛定谔方程决定。

电子在每个能态上的分布由费米－狄拉克统计决定。

一、电子气的能量状态索末菲提出，金属中传导电子能量状态（称为单电子的本征态），可以从在一定深度的势阱中运动的粒子的能态估算。

为了计算方便，通常设势径的深度是无限的（即金属外电子的势能为无穷大）E jσ=几个定性的结论●在T=0K时，k空间费米球中的量子态全部被电子占满，费米球外的量子态是空态。

●当温度T>0K时，由于热激发，费米面附近的电子可能跃迁到费米球以上的空态。

●只有费米面附件的电子才能导电和导热，●决定金属许多性质只是在费米面附近的那一小部分电子。

(在绝对零度时，波矢空间费米球中的量子态全部被电子占满，费米球外的量子态全部是空态。

由于泡利原理和没有激发能量，所有电子都被限制在费米面以下，有时形象地描述为电子被冻结在费米海中。

费米球深处的电子由于泡利原理的限制，如果没有足够的能量是不可能跃迁到费米球以上的。

或者说参与导电和导热的电子，其能量约等于费米能量，速度约等于费米速度。

金属自由电子理论Coca-cola standardization office【ZZ5AB-ZZSYT-ZZ2C-ZZ682T-ZZT18】第四章金属自由电子理论1.金属自由电子论作了哪些假设得到了哪些结果解：金属自由论假设金属中的价电子在一个平均势场中彼此独立，如同理想气体中的粒子一样是“自由”的，每个电子的运动由薛定谔方程来描述；电子满足泡利不相容原理，因此，电子不服从经典统计而服从量子的费米－狄拉克统计。

根据这个理论，不仅导出了魏德曼－佛兰兹定律，而且而得出电子气对晶体比热容的贡献是很小的。

2.金属自由电子论在k空间的等能面和费米面是何形状费米能量与哪些因素有关解：金属自由电子论在k空间的等能面和费米面都是球形。

费米能量与电子密度和温度有关。

3.在低温度下电子比热容比经典理论给出的结果小得多，为什么解：因为在低温时，大多数电子的能量远低于费米能，由于受泡利原理的限制基本上不能参与热激发，而只有在费米面附近的电子才能被激发从而对比热容有贡献。

4.驰豫时间的物理意义是什么它与哪些因素有关解：驰豫时间的物理意义是指电子在两次碰撞之间的平均自由时间，它的引入是用来描写晶格对电子漂移运动的阻碍能力的。

驰豫时间的大小与温度、电子质量、电子浓度、电子所带电量及金属的电导率有关。

5.当2块金属接触时，为什么会产生接触电势差解：由于2块金属中的电子气系统的费米能级高低不同而使热电子发射的逸出功不同，所以这2块金属接触时，会产生接触电势差。

6.已知一维金属晶体共含有N 个电子，晶体的长度为L ，设0=T K 。

试求：（1）电子的状态密度；（2）电子的费米能级；（3）晶体电子的平均能量。

解：(1)该一维金属晶体的电子状态密度为：dE dk dk dZ dE dZ E ⋅==)(ρ …………………………（1） 考虑在k 空间中，在半径为k 和dk k +的两线段之间所含的状态数为：dk L dk dZ π=∆=k 2 (2)又由于 mk E 222 = 所以 mk dk dE 2 = (3)将（2）和（3）式代入（1）式，并考虑到每个状态可容纳2个自旋相反的电子，得该一维金属晶体中自由电子的状态密度为：Em LE 22)( πρ= …………………………（4） （2）由于电子是费米子，服从费米—狄拉克统计，即在平衡时，能量为E 的能级被电子占据的几率为： 11)(+=-T K E E B Fe E f (5)于是，系统中的电子总数可表示为：⎰∞=0)()(dE E E f N ρ (6)由于0=T K ，所以当0F E E >，有0)(=E f ，而当0F E E ≤，有1)(=E f ，故（6）式可简化为：⎰=00)(FE dE E N ρ ＝⎰0022FE dE E m L π＝240F mE L π 由此可得： 222208mL N E Fπ= …………………………（7） （3）在0=T K 时，晶体电子的平均能量为： ⎰∞=00)()(1dE E E Ef N E ρ＝dE Em L E N FE 22100⎰⋅ π＝230)(232F E m N L π＝022223124F E mL N = π 7.限制在边长为L 的正方形中的N 个自由电子，电子的能量为)(2),(222y x y x k k mk k E += 。

物质结构与性质金属晶体与离子晶体一、金属共同的物理性质容易导电、导热、有延展性、有金属光泽等二、金属的结构1.“电子气理论”(自由电子理论)金属原子脱落来的价电子形成遍布整个晶体的“电子气”,被所有原子所共用，从而把所有的原子维系在一起。

2.金属键:这种金属原子间由于电子气产生的作用(在金属晶体中，金属阳离子和自由电子之间的较强的相互作用)。

3、金属晶体：通过金属键作用形成的单质晶体金属键强弱判断:阳离子所带电荷多、半径小－金属键强，熔沸点高。

三、金属晶体的结构与金属性质的内在联系金属为什么易导电？在金属晶体中，存在着许多自由电子，这些自由电子的运动是没有一定方向的，但在外加电场的条件下自由电子就会发生定向运动，因而形成电流，所以金属容易导电。

金属为什么易导热？金属容易导热，是由于自由电子运动时与金属离子碰撞把能量从温度高的部分传到温度低的部分，从而使整块金属达到相同的温度。

金属为什么具有较好的延展性？金属晶体中由于金属离子与自由电子间的相互作用没有方向性，各原子层之间发生相对滑动以后，仍可保持这种相互作用，因而即使在外力作用下，发生形变也不易断裂。

1、金属晶体的形成是因为晶体中存在A.金属离子间的相互作用B .金属原子间的相互作用C.金属离子与自由电子间的相互作用D.金属原子与自由电子间的相互作用2．金属能导电的原因是A.金属晶体中金属阳离子与自由电子间的相互作用较弱B .金属晶体中的自由电子在外加电场作用下可发生定向移动C .金属晶体中的金属阳离子在外加电场作用下可发生定向移动D .金属晶体在外加电场作用下可失去电子3、下列叙述正确的是A.任何晶体中，若含有阳离子也一定含有阴离子B .原子晶体中只含有共价键C.离子晶体中只含有离子键，不含有共价键D .分子晶体中只存在分子间作用力，不含有其他化学键4、为什么碱金属单质的熔沸点从上到下逐渐降低，而卤素单质的熔沸点从上到下却升高？四、金属晶体的密堆积结构1．下列有关金属元素特征的叙述中正确的是A．金属元素的原子只有还原性，离子只有氧化性B．金属元素在化合物中一定显正价C．金属元素在不同化合物中的化合价均不同D．金属单质的熔点总是高于分子晶体2．关于ⅠA族和ⅡA族元素的下列说法中正确的是A．同一周期中，ⅠA族单质的熔点比ⅡA族的高B．浓度都是0.01mol·L－1时，氢氧化钾溶液的pH比氢氧化钡的小C．氧化钠的熔点比氧化镁的高D．加热时碳酸钠比碳酸镁易分解关于离子晶体1、离子键2、成键的微粒：3、成键的本质：4、成键的条件：5.常见的离子化合物1、活泼的金属元素（IA、IIA）和活泼的非金属元素（VIA、VIIA）形成的化合物。