下载文档原格式
数学椭圆知识点总结数学椭圆知识点总结「篇一」1.椭圆的概念在平面内到两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹(或集合)叫椭圆.这两定点叫做椭圆的焦点，两焦点间的距离叫做焦距。
集合P={M||MF1|+|MF2|=2a}，|F1F2|=2c，其中a>0，c>0，且a，c为常数：(1)若a>c，则集合P为椭圆;(2)若a=c，则集合P为线段;(3)若a2.椭圆的标准方程和几何性质一条规律椭圆焦点位置与x2，y2系数间的关系：两种方法(1)定义法：根据椭圆定义，确定a2、b2的值，再结合焦点位置，直接写出椭圆方程。
(2)待定系数法：根据椭圆焦点是在x轴还是y轴上，设出相应形式的标准方程，然后根据条件确定关于a、b、c的方程组，解出a2、b2，从而写出椭圆的标准方程。
三种技巧(1)椭圆上任意一点M到焦点F的所有距离中，长轴端点到焦点的距离分别为最大距离和最小距离，且最大距离为a+c，最小距离为a-c。
(2)求椭圆离心率e时，只要求出a，b，c的一个齐次方程，再结合b2=a2-c2就可求得e(0(3)求椭圆方程时，常用待定系数法，但首先要判断是否为标准方程，判断的依据是：①中心是否在原点;②对称轴是否为坐标轴。
椭圆方程的第一定义：⑴①椭圆的标准方程：i. 中心在原点，焦点在x轴上. ii. 中心在原点，焦点在轴上。
②一般方程.③椭圆的标准参数方程：的参数方程为(一象限应是属于)。
⑵①顶点：或.②轴：对称轴：x轴，轴;长轴长，短轴长.③焦点：或.④焦距.⑤准线：或.⑥离心率.⑦焦点半径：i. 设为椭圆上的一点，为左、右焦点，则由椭圆方程的第二定义可以推出。
ii.设为椭圆上的一点，为上、下焦点，则由椭圆方程的第二定义可以推出。
由椭圆第二定义可知：归结起来为“左加右减”。
注意：椭圆参数方程的推导：得方程的轨迹为椭圆。
⑧通径：垂直于x轴且过焦点的弦叫做通经.坐标：和⑶共离心率的椭圆系的方程：椭圆的离心率是，方程是大于0的参数，的离心率也是我们称此方程为共离心率的椭圆系方程。
从课本看椭圆轨迹的求法一、待定系数法由不对称的两点确定椭圆方程时，由于焦点的位置不确定，一般可以用椭圆方程的一般形式，不必考虑焦点位置，直接用待定系数求解即可。
【例1】求经过两点)21,0(),31,31(-Q P 的椭圆的标准方程。
【答案】1415122=+y x 【解析】由于椭圆的焦点位置不确定，可以设椭圆方程的一般形式122=+ny mx 椭圆经过)21,0(),31,31(-Q P 两点，则 ⎪⎪⎩⎪⎪⎨⎧==+14199n n m ，解之得⎩⎨⎧==45n m 故所求椭圆的标准方程为1415122=+y x . 二、定义利用定义求椭圆方程，关键在于从题干中寻找“动点到两定点的距离和为常数”，找准这一关系式，则确定了标准方程中的a ，c 。
【例2】一动圆与圆22650x y x +++=外切，同时与圆226910x y x +--=内切，求动圆圆心M 的轨迹方程． 【答案】2213627x y += 【解析】设动圆圆心为),(y x M ，半径为R ，设已知圆的圆心分别为1O 、2O ， 将圆方程化解得()2234x y ++=，()223100x y -+=当⊙M 与1O 外切时，有12O M R =+，①当⊙M 与2O 内切时，有210O M R =-，② 将①②两式的两边分别相加，得1212O M O M +=，由椭圆的定义知，M 的轨迹是以1O 、2O 为焦点的椭圆则有3,6==c a ．从而所求椭圆方程为2213627x y +=. 【例3】如图，已知圆A ：22(1)16x y ++=，点(1,0)B 是圆A 内一个定点，点P 是圆上任意一点，线段BP 的垂直平分线1l 和半径AP 相交于点Q ，当点P 在圆上运动时，点Q 的轨迹为曲线C ，求曲线C 的方程。
【答案】13422=+y x 【解析】因为1l 是线段BP 的垂直平分线，所以||||QB QP =即42QA QB AP AB +==>=由椭圆定义可知Q 点的轨迹是椭圆，且3,1,2===b c a ，所以曲线C 的方程为13422=+y x . 三、直接法直接法是将题干中的几何关系直接转化，化简，在处理时要注意几何关系有意义的前提条件，最后判断方程的曲线，曲线的方程是否一一对应。
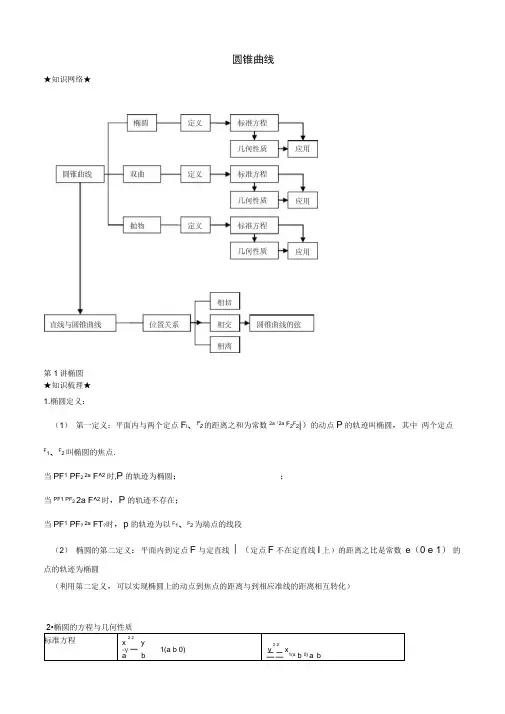
圆锥曲线★知识网络★第1讲椭圆★知识梳理★1.椭圆定义：（1）第一定义：平面内与两个定点F l、F2的距离之和为常数2a（2a |F2F2|）的动点P的轨迹叫椭圆，其中两个定点F1、F2叫椭圆的焦点.当PF1 PF2 2a F^2时,P的轨迹为椭圆；；当PF1 PF2 2a F^2时，P的轨迹不存在；当PF1 PF? 2a FT?时，p的轨迹为以F1、F2为端点的线段（2）椭圆的第二定义：平面内到定点F与定直线丨（定点F不在定直线I上）的距离之比是常数e（0 e 1）的点的轨迹为椭圆（利用第二定义，可以实现椭圆上的动点到焦点的距离与到相应准线的距离相互转化）★重难点突破★重点:掌握椭圆的定义标准方程，会用定义法和待定系数法、坐标转移法、求椭圆的标准方程，能通过方程 研究椭圆的几何性质及其应用难点:椭圆的几何元素与参数a，b ，c 的转换的关系1•要有用定义的意识则AB［解析］ABF 2的周长为4a 20， AB =8 2•求标准方程要注意焦点的定位4 m 1m 3［解析］当焦点在x 轴上时，22重难点：运用数形结合，围绕“焦点三角形” ，用代数方法研究椭圆的性质，把握几何元素转换成参数a,b,c2x问题1已知F l 、F2为椭圆251的两个焦过F i 的直线交椭圆于A 、B 两点若F 2A 122x问题2木椭圆4 2y_ m 1的离心率为 1 2，则m16m -综上 3或3★热点考点题型探析★ 考点1椭圆定义及标准方程 题型1:椭圆定义的运用［例1 ］(湖北部分重点中学2009届高三联考)椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭 圆反射后，反射光线经过椭圆的另一个焦点，今有一个水平放置的椭圆形台球盘，点 A 、B 是它的焦点，长轴长为2a ,焦距为2c ,静放在点 A 的小球(小球的半径不计) 次回到点A 时，小球经过的路程是 A . 4a B . 2(a — c) C . 2(a+c)D .以上答案均有可能［解析］按小球的运行路径分三种情况 ：(1)A C A ,此时小球经过的路程为 2(a — c);⑵A B D B A ,此时小球经过的路程为 2(a+c);⑶A P B Q A 此时小球经过的路程为 4a,故选D【名师指弓I 】考虑小球的运行路径要全面 题型2求椭圆的标准方程［例2 ］设椭圆的中心在原点，坐标轴为对称轴，一个焦点与短轴两端点的连线互相垂直，且此焦点与长轴上较近的端点距离为4、2 — 4,求此椭圆方程.【名师指引】准确把握图形特征，正确转化出参数 a ,b ,c的数量关系.［警示］易漏焦点在 y 轴上的情况. 考点2椭圆的几何性质题型1:求椭圆的离心率(或范围) ［例3 ］在厶ABC 中，A 30°,| AB| 2, S ABC 3 .若以A B 为焦点的椭圆经过点C ,则该椭圆的 离心率em 4 1 当焦点在y 轴上时，m 216~3，从点A 沿直线出发，经椭圆壁反弹后第【解题思路】将题中所给条件用关于参数a，b,c 的式子“描述”出来［解析］设椭圆的方程为2y b 22y 2 a1(a b0)则,b c 4(、2.2 2b c1)解之得:4 - 2 , b=c = 4•则所求的椭圆的方程为 2x 32 2y_ 16x 2或16 2红132【解题思路】由条件知三角形可解，然后用定义即可求出离心率1S ABC — |AB| |AC|si nA 屈 ［解析］2|AC| 2j3 |BC| J|AB|2| AC f 2|AB| |AC|cosA 2| AB| 2|AC| |BC| 2、3 2【名师指引】（1 ）离心率是刻画椭圆“圆扁”程度的量，决定了椭圆的形状；反之，形状确定，离心率也 随之确定 （2） 只要列出a 、b 、c 的齐次关系式，就能求出离心率（或范围） （3） “焦点三角形”应给予足够关注题型2:椭圆的其他几何性质的运用（范围、对称性等）P（x,y ），用x 表示y 后，把动点到直线的距离表示为 x 的函数，关键是要具有“函数思想” 考点4椭圆的综合应用题型：椭圆与向量、解三角形的交汇问题x 2［例4 ］已知实数x,y 满足42y_ 21 2 ，求X 2y X 的最大值与最小值2 2把x y X 看作X 的函数2X 2 y 1 21 2— y 2 x ［解析］由 4 2 得 21 2222 - X X 22 X 2yX 1 2 X X 2 1 2-(X 1) 3-,x ［ 2,2］22232 2 — 2 2当X 1时,x y x 取得最小值2 ,当x 2时，x y x取得最大值6 【名师指引】注意曲线的范围，才能在求最值时不出差错 考点3椭圆的最值问题题型：动点在椭圆上运动时涉及的距离、面积的最值2X［例5 ］椭圆161上的点到直线I ：y 9 0的距离的最小值为【解题思路】把动点到直线的距离表示为某个变量的函数［解析］在椭圆上任取一点P 设P （4cos ,3sin）.那么点P 到直线l 的距离为: 14cos 3sin1厂1212|【名师指引】也可以直接设点 【解题思0 1［例6］已知椭圆C 的中心为坐标原点 。
利用椭圆的参数方程求轨迹今天我们研究利用椭圆的参数方程求轨迹问题.已知椭圆的标准方程，则可以将椭圆的方程改写成参数方程，通过参数θ简明地表示曲线上任一点坐标，利用动点与椭圆上已知点的关系，建立坐标等式，消去参数化简得到动点的轨迹方程. 先看例题例：定点(0,2)A 与椭圆2221x y +=上的动点M 相连线段的中点的轨迹的参数方程为？注意椭圆的参数方程：中心在原点，坐标轴为对称轴的椭圆的参数方程有以下两种情况：焦点在x 轴上的椭圆：22221(0)x y a b a b +=>>，cos ,()sin x a y b θθθ=⎧⎨=⎩为参数. 焦点在y 轴上的椭圆：22221(0)y x a b a b +=>>，cos ,()sin x b y a θθθ=⎧⎨=⎩为参数. 以上的[)0,2θπ∈.例2：点P 为椭圆221691x y +=上异于长轴端点的任意一点，12,F F 是椭圆的两个焦点，求 12PF F 重心的轨迹方程.总结：1.一般处理此类问题，先利用椭圆的参数方程,设出椭圆上点的坐标，注意：如果是椭圆的一部分，要注意参数方程中参数θ的范围.2.利用动点与已知点的关系，建立有关动点的等式，得到参数方程.消去参数后得到动点的普通方程轨迹方程.练习题：1.已知点A在椭圆22114436x y+=上运动，点B（0，9）、点M在线段AB上，且12AMMB=，试求动点M的轨迹方程.2.已知椭圆方程为22221x ya b+=，椭圆长轴的左、右顶点分别为A1，A2，P是椭圆上任一点，引A1Q⊥A1P，A2Q⊥A2P，且A1Q与A2Q的交点为Q，求点Q的轨迹方程. 练习题解析：1.已知点A在椭圆22114436x y+=上运动，点B（0，9）、点M在线段AB上，且12AMMB=，试求动点M的轨迹方程.2.已知椭圆方程为22221x y a b+=，椭圆长轴的左、右顶点分别为A 1，A 2，P 是椭圆上任一点， 引 A 1Q ⊥A 1P ，A 2Q ⊥A 2P ，且A 1Q 与A 2Q 的交点为Q ，求点Q 的轨迹方程. 解：设椭圆的参数方程为cos ,(2sin x a y b θθθπθ=⎧≤<⎨=⎩为参数,且0). 则P 点坐标为 ()cos ,sin a b θθ ，由题意知，cos θ≠1，sin θ≠0 . ∵1sin cos A P b k a a θθ=+，2sin cos A P b k a a θθ=-， ∴111(cos 1),sin A Q A P a k k b θθ-+==- 221(cos 1).sin A Q A P a k k b θθ--==- ∴A 1Q 的方程为(cos 1)()sin a y x a b θθ+=-+ ① A 2Q 的方程为(cos 1)()sin a y x a b θθ-=-- ② ①×② ，得()()22222222222(cos 1)sin a a y x a x a b b θθ-=⋅-=-⋅-. 化简整理，得224221(0),x y y a a b +=≠即为所求的轨迹方程.。
而h ′1()x =12x，h ′2()x =-2x .由h ′1()x 0=h ′2()x 0得-12x 20=-2x 0，解得x 0，y 0=，所以p èø，则m =èø2+.画出h 1()x=12x和h 2()x =-x 2+m 的图象，如图1、2、3所示.由图可知，当m时，两个函数图象有1个交点；当m =时，两个函数图象有2个交点；当m 时，两个函数图象有3个交点.即当m >时，方程有1个根；当m =时，方程有2个根；当m 时，方程有3个根.将原方程解的个数转化为两个函数h 1()x =12x和h 2()x =-x 2+m 的交点的个数.而两个函数一定一动，确定两个函数图象相切时的位置，便可确定两个函数图象交点的个数.利用导数的几何意义便可求得切点的坐标，进而得到两图象相切时m 的取值.函数、方程之间的联系紧密.在解答含参方程问题时，我们要注意将问题转化为函数问题来求解，利用导数法、函数的图象来分析、解答问题.这样不仅能拓宽解题的思路，还能有效地提升解题的效率.(作者单位:江西省赣州市赣县中学)图1图2图3求解圆锥曲线轨迹问题的方法有很多，比如定义法、直接法、相关点法（或叫代入法）、参数法等.对于与椭圆有关的轨迹问题，我们也同样可以运用这些方法来求解.其中定义法是应用范围最广、使用频率最高的一种方法.而椭圆的定义有三种:第一、二、三定义,本文重点探讨如何运用椭圆的这三个定义来求解与椭圆有关的轨迹问题.一、椭圆的第一定义椭圆的第一定义：平面内与两个定点F 1,F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹.这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距.在求解与椭圆有关的轨迹问题时，我们可以直接套用椭圆的第一定义，寻找动点到两定点的距离之和，然后建立关系式,即∣F 1F 2∣=2c ,|PF 1|+|PF 2|=2a ,得到椭圆的焦距、长轴长，进而求得曲线的轨迹方程.例1.已知椭圆C ：x 2a 2+y 2b2=1(a >b >0)，M 为椭圆上的一个动点，F 1为椭圆的左焦点，则线段MF 1的中点P 的轨迹是（）.A.圆B.椭圆C.双曲线D.抛物线解析：不妨设椭圆C 的右焦点为F 2，根据椭圆的第一定义不难得到：|PF 1|+|PO |=12(|MF 1|+|MF 2|)=a >c ,根据椭圆的第一定义可知点P 的轨迹是椭圆.解：设椭圆C 的右焦点为F 2，坐标原点为O ，由椭圆的定义得|MF 1|+|MF 2|=2a >2c ，则|PF 1|+|PO |=12(|MF 1|+|MF 2|)=a >c ，则点P 的轨迹是以F 1、O 为焦点的椭圆，故本题答案为B 项.二、椭圆的第二定义圆锥曲线的第二定义：到定点的距离与到定直线的距离的比是e 的点的轨迹，其中定点为焦点，定直线为准线.当0<e <1时该曲线为椭圆；当e =1时该曲线为抛物线；当e >1时该曲线为双曲线.椭圆的第二朱园娇章长红解题宝典39解题宝典定义将焦半径的长度转化为到准线的距离，突出曲线上动点的横坐标.在解题时，我们只需要明确准线的位置和椭圆上的动点的横坐标，便可使问题得解.例2.已知点P 是正四面体V -ABC 侧面VBC 上一点，且点P 到底面ABC 的距离与它到顶点V 的距离相等，则动点P 的轨迹（）.A.线段B.圆的一部分C.椭圆的一部分D.双曲线的一部分解：过P 作PD ⊥平面ABC 于D ，过D 作DH ⊥BC 于H ，连接PH ，如图1，由题意可得BC ⊥平面DPH ，所以BC ⊥PH ，故∠PHD 为二面角V -BC -A 的平面角，令其为α，则在Rt△PDH 中，||PD :||PH =sin α，又点P 到平面ABC 距离与到点V 的距离相等，即||PV =||PD ，所以||PV :||PH =sin α<1，所以在平面VBC 中，点P 到点V 的距离与到直线BC 的距离之比为sin α<1，由椭圆的第二定义知P 点的轨迹为椭圆在平面VBC 内的一部分．解答这个题目的关键是作出并求得点P 到底面的距离.通过添加辅助线，设二面角V -BC -A 为α，由二面角的定义可得点P 到点V 的距离与定直线BC 的距离之比为一个常数，根据椭圆的第二定义即可得到问题的答案.三、椭圆的第三定义椭圆的第三定义也叫椭圆的斜率积定义，是指平面内动点到两定点A 1(a ,0)和A 2(-a ,0)的斜率的乘积等于常数e 2-1的点的轨迹.其中两定点为椭圆的顶点.椭圆的第三定义将斜率的乘积作为主要关系，那么我们在解题时可以根据斜率的这种关系来进行求解.例3.设P 为椭圆C :x 2a 2+y 2b2=1(a >b >0)上的动点，F 1,F 2为椭圆的两个焦点，I 为△PF 1F 2的内心，求点I的轨迹方程．解析：由于本题是与焦点三角形的内切圆有关的问题，所以要依据分割图形的面积来寻找圆的半径和三角形三边之间的关系.由内心I 是动点，F 1和F 2是两个定点，我们可联想到椭圆的第三定义，结合这两个关系式得到IF 1与IF 2的斜率之积是一常数，根据椭圆的第三定义就不难发现并求得点I 的轨迹方程.解：如图2，设内切圆I 与F 1F 2的切点为H ，半径为r ，且设F 1H =y ，F 2H =z ,PF 1=x +y ,PF 2=x +z ,c =a 2+b 2，则{y +z =2c ,2x +y +z =2a ,所以直线IF 1与IF 2的斜率之积为k IF 1∙k IF 2=-IH 2F 1H ∙F 2H=-r 2yz ，而根据海伦公式可得△PF 1F 2的面积为()x +y +z r =xyz ()x +y +z ，因此k IF 1∙k IF 2=-x x +y +z =-a -ca +c .根据椭圆的斜率积定义可得I 点的轨迹是以F 1F 2为长轴，离心率为e 的椭圆，其标准方程为x 2c 2+y 2a -c a +c∙c 2=1()y ≠0.我们知道，椭圆中有个重要的结论：椭圆x 2a 2+y 2b2=1(a >b >0)上任意一点到椭圆长轴的两个端点的斜率之积等于-b2a2.椭圆的第三定义是这个结论的逆命题.因此，对于椭圆中与角度、斜率有关的问题，我们都可以利用椭圆的第三定义，根据椭圆中与角度、斜率建立关系式，求得椭圆的方程.以上三个题目分别借助椭圆的第一定义、第二定义、第三定义求解与椭圆有关的轨迹问题.在解题过程中，我们要学会依据题意，结合图形，紧扣椭圆的三个定义对题目中的条件进行转化，比如，例1是根据椭圆的第一定义将中位线转化为动点到两定点的距离之和，例2是根据椭圆的第二定义，将点P 到平面ABC 距离与到点V 的距离之间的关系转化为点P 到点V 的距离与到直线BC 的距离之比，例3是根据椭圆的第三定义，将圆的半径和三角形三边之间的关系转化为k IF 1∙k IF 2.通过转化便可建立动点满足的等量关系式，联系椭圆的定义，从而达到解答与椭圆有关的轨迹问题的目的.(作者单位:江西省余干第一中学)图1图240。
解 题 研 究J I E T I Y A N J I U解决一类椭圆切线有关的轨迹问题的策略探究—以 2014 年高考数学广东卷文 / 理科第 20 题为例赵银仓 （广 省 莞市 莞中学）摘要：从不同 面 的两条切 相交 生的交点 迹 展开分析， 找适 学生思 的表征方式，突破 的障碍， 化解决的策略，以提高学生分析 与解决 的能力及思 能力.关键词： 切 ； 迹 ；策略探究2014 年高考数学广东卷文 / 理科第 20 题：已知椭圆 C ： x 2 + y 2= 1（a > b > 0）的一个焦点为（姨5 ，0），a 2b 2离心率为 姨5.3（1）求椭圆 C 的标准方程；（2）若动点 P （x 0，y 0）为椭圆 C 外一点，且点 P到椭圆 C 的两条切线相互垂直，求点 P 的轨迹方程.立二者的方程，减元化 一元二次方程利用判 式 0 来化. 因此 用恰当的方式表示切 的方程，在已知切 点 P 的情况下， 其斜率是常用策略.解法 1：当过点 P （x 0 y 0， ）的两条切线斜率存在时， ） 则切线方程可统一设为 y - y 0 = k （x - x 0 .x 2 y 22 2联立椭圆方程 + = 1，消去 y ，得（4 + 9k ）x +9 4 （ （ 2）- 36 = 0.18k y 0- kx 0）x + 9 y 0- kx 0判别式2 22（22= 18 k （y 0））［（）-- kx- 36 4 + 9k y 0- kx 04］= 0，化简，得（y 0 - kx 0）2 - 9k 2 - 4 = 0，即（x 20 - 9）k 2 - 2x 0y 0k + y 20 - 4 = 0.y 2- 4 依题意，得 k 1·k 2 == -1，x 20 - 9这是关于椭圆的两条切线相交产生的交点轨迹问 即 x 02 + y 02 = 13.题，绝大多数学生不能有效地表征问题，找不到合理当两条切线的斜率有一条不存在时，结合图象的解决途径，或有一点思路却无法实施解题计划. 下 （ 略） 得 P 是直线 x = -3，x = 3，y = 2，y = -2 的面从不同层面对问题展开分析，寻找适应学生思维状 四个交点，都满足 x 02 + y 02 = 13， 况的表征方式，突破问题的障碍，优化解题策略，提故点 P 的轨迹方程为 x 2 + y 2 = 13.升思维能力.解法 2：同解法 1，由判别式 = 0，得（y 0 - kx 0） -2一、策略探究9k 2 - 4 = 0.姨 k 姨 k 2 ，- - 4 = 0 容易得到椭圆 C 的标准方程为 x 2 + y 2 = 1，难点 0220. 在于第（）问的解决策略探究 9 4即（y 0k + x 0） - 9 - 4k =.以上二式相加，可得 x 02 + y 02 = 13.2下同解法 1，略.策略 ：引入斜率表示切线方程，用判别式来确1定位置关系.【评析】引入斜率作为参数，可方便地表示出切线 分析：解决 曲 与直 相切 的通法是方程，判别式为 0 揭示二者相切的本质. 解法 1 基于收稿日期：2014—09—15作者简介：赵银仓 （1963—），男，中学高 教 ，主要从事高中数学教育及教学研究．2015 年第 1—2 期107解题研究J I E T I Y A N J I U对两条切线具有相同的性质，它们的斜率适合同一个方程这一隐性条件的挖掘；而解法2 则应用了类比推理，在得到两个方程的情况下，结合方程组的特点整体消参. 两种解法异曲同工，运用设参，消参，化简这一思维策略.策略 2：联立两条切线方程，采用整体消参策略.分析：的著特点“点 P 到 C 的两条切相互垂直”，可化“点P 为椭圆 C 的两条相互垂直切的交点”，引入其中一条切的斜率参数来表示两条切的方程，立方程求解.解法 3：由解法 1 知，= 0，（kx0 - y0）2 - 4 - 9k2 = 0.所以 kx0 - y0 = ±姨4 + 9k2 .因为过点 P（x ，y）的切线方程为 y - y = k（x - x），0000 即 y - kx = y0 - kx0，所以一条切线方程为 y = kx ±姨4 + 9k2，即 y - kx = ±姨4 + 9k2 .同理，另一条切线方程为 y = - k 1x ±姨4 +k 92，即 x + ky = ±姨4k2 + 9 .以上二式平方相加，得（1 + k2）（x2 + y2）=（1 + k2）（4 + 9），即 x2 + y2 = 13.下同解法 1，略.【评析】联立两条切线的方程就可用斜率表示点P 的坐标，即得动点P 的参数方程. 事实上，观察两条切线方程的结构特征，就能整体消掉斜率求得普通方程，即用交迹法来求动点的轨迹方程.策略 3：以切点坐标为参数，运用导数突破难点.分析：比抛物，可通数求得其上一点的切的斜率，因而先研究用数来表示上任一点的切的斜率.引理：过椭圆x2 +y2= 1 上的任一点 M（x1，y1） a2 b2作椭圆的切线，则该切线方程为 b2x1x + a2y1y = a2b2.引理的证明可从如下二个角度来思考.思路 1：用通法证明，通过联立方程让判别式为0 来推理论证.当切线的斜率 k 存在时，设过点 M（x1，y1）的切线方程为 y - y = k（x - x），1 1联立椭圆方程x2 y2 2 2 2 2+ = 1，消去 y，得（b + a k）x +a2 b22 ） 2 2 2 2（）- a b = 0.2a k（y1 - kx1 x + a y1 - kx12 2 2 2 2= 0.整理得（x1 - a）k - 2x1y1k + y1 - b2 （ 2 2 2当 x1≠±a 时，经验证））（-1 =（2x1y1 - 4 x1 - a y12 2 2 2 2 2 20.b）= 4（b x1 + a y1 - a b）=解得 k = x1y1 .x12 - a2又因为x12 + y12 = 1，a2 b2可得 a2 - x12 = a2y12 .b22所以 k = - b x1 .2a y1所以过点 M 的切线方程为 y - y1 = - b2x1 ），a y1即 b2x1x + a2y1y = a2b2.当 x1 = ±a 时，y1 = 0，此时斜率不存在，切线方程为 x = ±a 也适合.综上，过点 M 的切线方程为 b2x1x + a2y1y = a2b2.思路2：用导数的几何意义证明，即导数表示在该点处曲线的斜率. 不过要注意在椭圆方程中将 y 理解为 x 的隐函数，方可求导.由椭圆的方程x2+y2= 1，得1y2 = 1 -1x2.a2 b2 b2 a2 两边分别看成关于 x 的函数，求导，b22 y·y′ = - a22 x，即y′ = -b2x（y1≠0）.a2y以下同思路 1，略.解法 4：过点 P 引椭圆 C 的两条切线，设切点分），（，）别为 A（x1，y1 B x2 y2 .则切线 PA 的方程为 4x1x + 9y1y = 36，切线 PB 的方程为 4x2x + 9y2y = 36.，），因为切线 PA，PB 都过点 P（x0 y0所以 4x0x1 + 9y0y1 = 36，4x0x2 + 9y0y2 = 36.又因为x12 + y12 = 1，x22 + y22 = 1，49 9 4≠≠4x0x + 9y0y = 36，所以（，），（，）都是方程组 2 2y≠4≠ 92015 年第 1—2 期的解.消去 y，整理得（9y20 + 4x20）x2 - 72x0x + 4 × 81 - 81y02 = 0. ①所以 x x = 81（9 - x 22）. ②1 29y02 + 4x02同理，y y = 16（9 - x02）. ③9y02 + 4x021 2因为 PA⊥PB，所以 16x1x2 + 81y1y2 = 0. ④将②，③代入④，16 ×81（4 - y02）+ 81 ×16（9 - x02）= 0，9y02 + 4x029y02 + 4x02即 x20 + y20 = 13.所以点 P 的轨迹方程为 x20 + y20 = 13.解法 5：同解法 4，由方程①，可得x + x = 72x0 ，x x = 81（4 - y02）.9y02 + 4x021 2 1 29y02 + 4x02由 16x1x2 + 81y1y2 = 0，两边乘以 y20，得2）（），16y0 x1x2 +（36 - 4x0x1 36 - 4x0x2 = 02 2 （）即（x0 + y0）x1x2 - 9x0 x1 + x2 + 81 = 0.解题研究J I E T I Y A N J I U 为 A（x1，y1），B（x2，y2）.当 y0≠0 时，则弦 AB 所在直线的斜率存在.设其方程为 y = kx + b，与椭圆方程x2 +y2 = 1 联 9 4 立，消去 y，得（4 + 9k2）x2 + 18kbx + 9b2 - 36 = 0.= 182k2b2 - 36（4 + 9k2）（b2 - 4）> 0，即 9k2 - b2 + 4 > 0.所以 x1 + x2 = - 18kb ，x1x2 = 9b2 - 36 .4 + 9k2 4 + 9k2因为 PA⊥PB，所以 16x1x2 + 81y1y2 = 0，即 16x1x2 + 81（kx1 + b）（kx2 + b）= 0.2） 2= 0.变形，得（16 + 81k）x1x2 + 81kb（x1 + x2 + 81b代入整理，得 13b2 - 81k2 = 16.所以 9k2 - b2 + 4 =3613（1 + k2）> 0 恒成立.因为弦 AB 的方程可表示为 4x0x + 9y0y =36，所以 k = -4x0，b =4，x20 + y20 = 13.9y0y0当 y0 = 0 时，则直线 PA，PB 的斜率分别为±1，可所以81（4 - y02）（x02 + y02）-9x0·72x0+ 81 = 0.求得 x0 = ±姨13 .9y02 + 4x02 9y02 + 4x02 所以点 P 的轨迹方程为 x02 + y02 = 13.化简，得 x02 + y02 = 13.【评析】待定切点弦直线方程，将问题条件“两条【评析】以切点坐标为参数，可以快捷地写出斜切线相互垂直”转化为斜率与截距之间的关系，再利率，表示出切线方程，发现切点弦方程，运用韦达用点 P 的坐标来表示切点弦的方程，这样就找到点的定理得到参数与变量之间的关系，同样将“两条切坐标、斜率与截距之间的关系，代入即得所求方程. 线相互垂直”转化为切点坐标之间的关系，代入消这种“算两次”的方法其实就是一种等量传递，其作参，难点在于整理运算. 解法 4 与解法 5 基本相同，用就是简化过程.二者同为代入消参. 区别在于前者利用两个切点的策略 5：观察特殊情形，归纳并验证一般情形.横坐标之积与纵坐标之积的对称性，由横坐标之积分析：察、、明是数学探究中常用的表达式，类比得出纵坐标之积的表达式，而后者的策略，特是理疑可从特殊情形入手. 则是直接消去纵坐标，利用韦达定理消参，消参的此而言，容易想到教材中在研究的范途径不同. 所用的外切矩形，其点到中心（原点）的距离恰策略 4：从切点弦方程入手，实施“算两次”以、短半两直角的直角三角形的斜. 这策略. 个是否具有一般性？可从外切矩形角的分析：把两个切点看作两个切点的弦所在的度是否改入手探究.直与的交点，待定切点弦直方程并与方程立，消元用达定理沟通各参量与量之的系.解法 6：设过点 P（x0，y0）的两条切线的切点分别解法 7：设 P（x ，y）关于原点的对称点 P（′-x ，-y），0000 则由椭圆关于原点成中心对称知，过点 P 与点 P′分别引椭圆的两条切线，依题意知它们围成一个中心在原点的矩形.109 2015 年第 1—2 期解 题 研 究 J I E T I Y A N J I U由解法 3 知，一组平行切线方程为 y = kx± 姨4 + 9k 2 ，即 kx - y ± 姨4 + 9k 2 = 0.则 它们之间的距离，即矩形的一边长为 d 1 =2 姨4 + 9k 2. 姨k 2+ 1同理，另一组切线方程为 y = - k 1x ±姨4 +k92 ，即 x + ky ± 姨4k 2 + 9 = 0.则它们之间的距离，即矩形的另一边长为 d 2 = 2姨4k 2+ 9 . 姨k 2 + 1所以PP ′ = 姨d 12 + d 2222+ 9）=姨4（4 + 9k ）+4（4k1 + k 21 + k 2= 2 姨13所以 OP =12 PP ′ = 姨13 ，即 x 20 + y 20 = 13.下同解法 3，略.）的两条切线的 解法 8：同解法 7，设过点 P （x 0，y 0切点分别为 A （x 1，y 1），B （x 2，y 2），则切线 PA 的方程为 4x 1x + 9y 1y = 36，切线 PB 的方程为 4x 2x + 9y 2y = 36.， ）的两条切线的切点分别同理，设过点 P （′-x 0-y， ）， （ ， ），为 C （-x 1 -y 1 D -x 2-y 2则切线 P ′C 的方程为 4x 1x + 9y 1y = -36，切线 P ′D11= 36姨+ 81 - 5x 12 81 - 5x 2281 × 2 - 5（x 2 + x 2）= 36姨1812 - 81 × 5（x 21 + x 22）+ 25x 21 x 2213［81 × 2 - 5（x 2 + x 2）］= 36姨1213 × 812 - 81 × 65（x 21 + x 22）+ 45 × 81（x 21 + x 22 - 9） = 2 姨13 . 所以 OP =12 PP ′ = 姨13 ，即 x 20 + y 20 = 13.故点 P 的轨迹方程为 x 20 + y 20 = 13.【评析】显然，通过表示出两条切线方程，求出交点，再来验证对角线的长度不变运算量会很大，十分不便. 解法 7 与解法 8 都是通过用两条平行线间的距离公式使运算量大幅降低. 区别在于前者以斜率为参数研究不变性，而后者以切点坐标为参数研究不变性，其推理过程稍多些.策略 6： 引入椭圆的参数方程，化归三角恒等 变形.分析： 的参数方程以角度表示坐 ，可将化 三角 ，借助于三角运算的灵活性 程的 化与思的 化.解法 9：设过点 P （x ，y ）的两条切线的切点分别0 0为 A （3cos α，2sin α），B （3cos β，2sin β）， 则切线 PA 的方程为 2xcos α + 3ysin α = 6，切线 PB 的方程为 2xcos β + 3ysin β = 6. 由椭圆关于原点成中心对称图形知，过点 P （′-x ，-y ）0 0的方程为 4x 2x + 9y 2y = -36. 的两条切线分别与 PA ，PB 平行，四条切线围成的矩四条切线围成的矩形的边长分别为 d 1=72 ， 形的边长如下：11d 1 = 12d 2 = 72 .姨4cos α + 9sin α 姨16x 22 + 81y 22 d 2 = 12因为 4x 12 + 9y 12 = 36，4x 22 + 9y 22 = 36，PA ⊥PB ， 姨4cos β + 9sin β所以 16x 1x 2 + 81y 1y 2 = 0. 因为 PA ⊥PB ，162x 12 x 22 = 812y 12 y 22 ，所以 4cos αcos β + 9sin αsin β = 0.代入化简，得 16x 12 x 22 = 81（9 - x 12）（9 - x 22），65x 12 x 22 =化简，得 16cos 2αcos 2β = 81sin 2αsin 2β，65cos 2αcos 2β = 81 × 9（x 12 + x 22 - 9）.81（cos 2α + cos 2β - 1）.所以 PP ′ 所以 PP ′= 姨d 12 + d 22= 姨d 12 + d 22122122=72 2+72 2=姨+2 2222222姨16x 1+ 81y116x 2 + 81y 24cos α + 9sin α4cos β + 9sinβ1102015 年第 1—2 期解 题 研 究J I E T I Y A N J I U法 9 沿用前面验证外切矩形对角线的长度不变的策略，= 12姨11+而解法 10 则直面问题，用两个参数表示交点坐标，直9 - 5cos 2α9 - 5cos 2β接验证交点到中心 （原点） 的距离不变这一特征，过18 - 5（cos 2α + cos 2β）= 12（9 - 5cos 2α）（9 - 5cos 2β）程看似难，其实由于三角变形的灵活性运算过程并不姨= 12姨18 - 5（cos 2α + cos 2β）复杂.81 - 45（cos 2α + cos 2β）+ 25cos 2αcos 2β二、反思感悟= 12姨13［18 - 5（cos 2α + cos 2β）］13× 812 - 13 × 45（cos 2α+cos 2β）+ 5 × 81（cos 2α+cos 2β-1）数学问题解决的必要条件是对问题进行合理的表= 2姨13 .征，即通过认真分析审视问题，全面把握理解问题中所以，1，OP= PP ′ = 姨 13所含的数学结构，通过联想转化为自己容易理解的另2即 x 02 + y 02 = 13.一个数学结构. 这种对数学问题表征的方式直接影响故点 P 的轨迹方程为 x 02 + y 02 = 13.着问题解决的思维策略. 如果能从多种不同角度对问解法 10： 设切点分别为 A （3cos α， 2sin α）， 题进行理解，充分挖掘自己的不同模块的知识经验， B （3cos β，2sin β）， 形成理解问题的不同的表征方式，就可以拓宽问题的则切线 PA 的方程为 2xcos α + 3ysin α = 6，切线理解与转化渠道，从而可选择接近问题本源，解决问 PB 的方程为 2xcos β + 3ysin β = 6.题相对快捷的方法与策略，这样就打开了解决问题的3（sin β - sin α）通道. 如前述广东高考解析几何试题，大多数学生在联立以上二个方程，可解得 x =，sin （ β - α） 平时的学习中，缺少对问题表征能力的培养，在高考2（cos β - cos α）y =，即点 P 轨迹的参数方程.时无法找到适合自己的问题表征方式，因而无法形成 sin （ α - β）消去参数化为普通方程， 解决问题的有效途径. 如果能够从参数的选择，观察 因为 PA ⊥PB ，归纳等不同角度来表征问题，就形成以切线的斜率为 所以 4cos αcos β + 9sin αsin β = 0.参数，结合韦达定理消参或联立两条切线方程整体消变形整理，得 65cos 2αcos 2β = 81（cos 2α + cos 2β - 1）. 参，以切点坐标为参数，运用导数列切线方程消参求2 2解，观察特殊情形通过外切矩形的对角线入手，这样 所以 x 2 + y 2 =就极大地拓展了问题解决的思路，并发现以斜率为参sin （β - α）=18 - 5（cos2α+ cos 2β）.数这个表征方式接近问题的本质，思维直接，过程简sin （2β -α）2便. 在高三教学中，要经常引导学生对综合问题进行 因为 sin （β - α）多元表征训练，这样会加强学生的审题能力、理解能 = sin 2βcos 2α + cos 2βsin 2α - 2sin αsin βcos αcos β2222822力、推理能力与运算能力，提升分析问题与解决问题=（1 - cos β）cos α + cos β（1 - cos α）+ cos α + cos β的思维能力，从而实现提高学生分析问题与解决问题 92 2 10 2 2能力的教学目标.= cos α + cos β -cos αcos β 9 参考文献：= cos 2α + cos 2β - 10 × 81（cos 2α + cos 2β - 1）［1］曹才翰，章建 ． 数学教育心理学［M ］. 北96518 - 5（cos 2α + cos 2β）京：北京 范大学出版社，2006. =，13［2］ ． 解析几何中一 典型 解的分析［J ］.代入上式，得点 P 的轨迹方程为 x 2 + y 2 = 13. 中国数学教育（高中版），2012（9）：34－36.【评析】引入椭圆参数方程表示切点坐标，以角度 ［3］赵银仓． 解决一 抛物 切 的策略与 为参数表示切线方程，将问题条件“两条切线相互垂 困因分析［J ］. 中学教研（数学），2014（1）： 直”转化为关于切点坐标参数的两个角度的关系. 解15－19.111 2015 年第 1—2 期。
第三课时：与椭圆有关的轨迹方程学习目标：1、通过学习进一步理解椭圆的标准方程，并能在具体问题中具体选择解决问题； 2、能利用所学知识解决简单的轨迹问题；3、在解决问题过程中进一步体会“坐标法”在解决几何问题中的应用． 学习重点：简单的轨迹问题．学习难点：选择适当的方式求动点的轨迹（轨迹方程）．学法指导：同学们，求轨迹（轨迹方程）是解析几何中一类重要的题型，通过本节课的学习要体会求轨迹（轨迹方程）常用的方法．复习回顾：问题1：同学们，前面我们学习了椭圆的标准方程，请大家完成下表．自主学习：问题2：同学们，求轨迹（轨迹方程）是解析几何中常见的一类重要题型，例如，推导圆的标准方程其实就是求平面内满足到定点（圆心）的距离等于定长（半径）的动点的轨迹方程；推导椭圆的标准方程其实就是求平面内满足到定点21,F F 的距离的和为常数（大于||21F F ）的动点的轨迹方程，这是利用某些曲线的定义求轨迹方程的方法的具体体现，这种方法称为直接法 请同学们完成课本（理）42页（文）36页练习第4题问题3：同学们，求轨迹方程除了直接法，常用的还有变量代人法，请理科同学阅读教材第41页例2，文科同学阅读教材第34页例2，对照必修2第122页例5，认真体会，并完成下面的高考题。
椭圆的标准方程图像焦点坐标焦距 c b a ,,的关系焦点在x 轴上焦点在y 轴上（陕西理）如图，设P 是圆2225x y +=上的动点，点D 是P 在x 轴上的投影，M 为 PD 上一点，且|MD|=45|PD| （Ⅰ）当P 在圆上运动时，求点M 的轨迹C 的方程；（Ⅱ）求过点（3，0）且斜率为45的直线被C 所截线段的长度问题4：请理科同学完成教材41页的“思考”，文科同学完成教材35页“思考”问题5：理科同学阅读教材41页例3，文科同学阅读教材35页例3，回答以下问题 （1）、例3采用了哪种求轨迹方程的方法？ （2）、教材中为什么把5,5-==x x 舍掉？ 重要结论：（1）设21,A A 是椭圆12222=+bya x 长轴的两个端点，M 是椭圆上除21,A A 外的任意一点，则直线21,MA MA 的斜率之积为定值：21MA MA k k ⋅=22ab -（2）设21,B B 是椭圆12222=+bya x 短轴的两个端点，M 是椭圆上除21,B B 外的任意一点，则直线21,MB MB 的斜率之积为定值：21MB MB k k ⋅=22ab -完成下面高考题（2013年）在平面直角坐标系x O y 中，已知圆P 在x 轴上截得线段长为22，在y 轴上截得线段长为23，求圆心P 的轨迹方程第三课时：与椭圆有关的轨迹方程1、理科教材49页A组6，7，题，B组1,2，文科教材42页第6，7题，B组1,22、（2013年新课标卷）已知圆M：22x y-+=，动圆P(1)9(1)1x y++=，圆N：22与圆M外切，并且与圆N内切，圆心P的轨迹为曲线C（1）求C的轨迹方程（2）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|3、已知动圆过定点（4,0），且在y 轴上截得的弦MN 的长为8，求动圆圆心C 的轨迹方程4、已知定点M （-3,4），O 为坐标原点，定点N 在圆x 2+y 2=4上运动，以OM ，ON 为两边作平行四边形MONP ，求点P 的轨迹方程5、椭圆14922=+y x 的长轴的两个端点A 1(-3,0),A 2(3,0)，21,P P 是垂直于直线21A A的弦的端点 ，求直线11P A 与22P A 交点P 的轨迹方程6、（选做）已知椭圆C 过点A 31,2⎛⎫⎪⎝⎭,两个焦点分别为F 1（-1,0），F 2（1，0）（1）求椭圆C 的方程（2）E,F 是椭圆C 上的两个动点，如果直线AE 的斜率与AF 的斜率互为相反数，证明直线EF 的斜率为定值，并求出这个值2A1A2p1pPO xy7.（陕西理17）如图，设P 是圆2225x y +=上的动点，点D 是P 在x 轴上的投影，M 为PD 上一点，且45MD PD =（Ⅰ）当P 在圆上运动时，求点M 的轨迹C 的方程；（Ⅱ）求过点（3，0）且斜率为45的直线被C 所截线段的长度 解：（Ⅰ）设M 的坐标为（x,y ）P 的坐标为（xp,yp ）由已知得,5,4xp x yp y =⎧⎪⎨=⎪⎩∵P 在圆上， ∴ 225254x y ⎛⎫+= ⎪⎝⎭，即C 的方程为2212516x y +=（Ⅱ）过点（3，0）且斜率为45的直线方程为()435y x =-，设直线与C 的交点为()()1122,,,A x y B x y将直线方程()435y x =-代入C 的方程，得()22312525x x -+= 即2380x x --=∴12341341,22x x -+== ∴ 线段AB 的长度为()()()22212121216414114125255AB x x y y x x ⎛⎫=-+-=+-=⨯=⎪⎝⎭（2013年新课本卷）已知圆M ：22(1)1x y ++=，圆N ：22(1)9x y -+=，动圆P 与与圆M 外切，并且与圆N 内切，圆心P 的轨迹为曲线C（3）求C 的轨迹方程（4）l 是与圆P ，圆M 都相切的一条直线，l 与曲线C 交于A ，B 两点，当圆P 的半径最长时，求|AB |21.【2012辽宁理2】如图，椭圆0C ：22221(0x y a b a b+=>>，a ，b 为常数)，动圆22211:C x y t +=1b t a <<。
