与椭圆有关的轨迹问题

椭圆方程与轨迹问题 〖1〗如图,斜线段ΑΒ与平面α所成的角为60,Β为斜足,平面α上的动点Ρ满足30ΡΑΒ∠=,则点Ρ的轨迹是( )A.直线B.抛物线C.椭圆D.双曲线的一支〖2〗如图AB 是长度为定值的平面α的斜线段,点A 为斜足,若点P 在平面α内运动,使得ABP ∆的面积为定值,则动点P 的轨迹是 A.圆 B.椭圆 C 一条直线 D 两条平行线〖3〗已知椭圆C 的方程为22221(0)x y a b a b +=>>,右焦点为(2,0)F ,且离心率为63. 求椭圆C 的方程.〖4〗已知椭圆2222:1(0)x y C a b a b+=>>的离心率为22,且过点(2,1)A .求C 的方程.〖5〗已知椭圆2222:1x y E a b+=(0a b >>)的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线:l 3y x =-+与椭圆E 有且只有一个公共点T .求椭圆E 的方程.〖6〗如图,椭圆2222:1x y E a b+=(0a b >>)的离心率是22,点(0,1)P 在短轴CD 上,且1PC PD ⋅=-.求椭圆E 的方程.〖7〗已知动点(,)M x y 到直线:4l x =的距离是它到点(1,0)N 的距离的2倍. 求动点M 的轨迹C 的方程.〖8〗已知动点P 到直线334-=x的距离是到定点(0,3-)的距离的332倍.求动点P 的轨迹方程.〖9〗动点(,)P x y 满足22(1)(2)|3410|a x y x y -+-=+-，且P 点的轨迹是椭圆，则a 的取值范围是___________________．〖10〗*空间点到平面的距离定义如下:过空间一点作平面的垂线,这个点和垂足之间的距离叫做这个点到这个平面的距离.已知平面,,两两互相垂直,点A ∈,点A 到,的距离都是3,点P 是上的动点,满足P 到的距离是P 到点A 距离的2倍,则点P 的轨迹上的点到的距离的最大值是( ) (A) (B) (C)33+ (D)6αβγαβγαβγ33-3〖11〗已知点(2,0)A -,(2,0)B ,动点(,)M x y 满足直线AM 与BM 的斜率之积为12- .记M 的轨迹为曲线C .求C 的方程,并说明C 是什么曲线.〖12〗在平面直角坐标系xOy 中,点B 与点(1,1)A -关于原点O 对称,P 是动点,且直线AP与BP 的斜率之积等于13-.求动点P 的轨迹方程. 〖13〗已知(4,0)M 、(1,0)N ，若动点P 满足||6PN MP MN =⋅.求动点P 的轨迹方程. 〖14〗已知向量(,3),(1,0)a x y b ==，且(3)(3)a b a b +⊥-．求点(,)Q x y 的轨迹C 的方程．〖13〗设Q 、G 分别为ABC ∆的外心和重心,已知)0,1(-A ,)0,1(B ,AB QG //.求点C 的轨迹E .〖14〗在ABC ∆中，两个定点)0,3()0,3(B A -，ABC ∆的垂心H （三角形三条高线的交点）是AB 边上高线CD 的中点.求动点C 的轨迹方程.〖15〗在ABC ∆中,顶点(1,0)B -、(1,0)C ,G 、I 分别是ABC ∆的重心和内心,且IG ∥BC .求顶点A 的轨迹M 的方程.〖16〗已知点(3,0),(3,0)A B -,动圆222:(5)()(0)M x y a a a -+-=≠，分别过A 、B 作动圆M 的切线,两切线（非x 轴）交于点P .求动点P 的轨迹方程.〖17〗设P 是圆2225x y +=上的动点,点D 是P 在x 轴上的投影,M 为线段PD 上一点,且4||||5MD PD =.当P 在圆上运动时,求点M 的轨迹C 的方程. 〖18〗点P 为圆229x y +=上任意一点，过P 作x 轴的垂线，垂足为Q ，点M 在PQ 上，且2PM MQ =，则点M 的轨迹方程为_______________.〖19〗设O 为坐标原点,动点M 在椭圆C 上,过M 作x 轴的垂线,垂足为N ,点P 满足2NP NM =.求点P 的轨迹方程.〖20〗已知B A 、分别是x 轴和y 轴上的两个动点，满足2=AB ，点P 在线段AB 上且PB AP 2=，设点P 的轨迹方程为C ．求曲线C 的方程．〖21〗已知动点A 、B 分别在x 轴、y 轴上，且满足||2AB =，点P 在线段AB 上，且(AP tPB t =是不为零的常数),设点P 的轨迹方程为C .求点P 的轨迹方程C .〖22〗一种画椭圆的工具如图1所示.O 是滑槽AB 的中点,短杆ON 可绕O 转动,长杆MN通过N 处铰链与ON 连接,MN 上的栓子D 可沿滑槽AB 滑动,且1DN ON ==,3MN =.当栓子D 在滑槽AB 内作往复运动时,带动．．N 绕O 转动,M 处的笔尖画出的椭圆记为C .以O 为原点,AB 所在的直线为x 轴建立如图2所示的平面直角坐标系.求椭圆C 的方程.〖23〗△ABC 的两个顶点为(4,0),(4,0)A B -,△ABC 周长为18,则C 点轨迹为( )A.221(0)259x y y +=≠ B. 221(0)259y x y +=≠ C.221(0)169x y y +=≠ D. 221(0)169y x y +=≠ 〖24〗已知A 、B 为坐标平面上的两个定点，且||2AB =，动点P 到A 、B 两点距离之和为常数2，则点P 的轨迹是A.椭圆B.双曲线C.抛物线D. 线段〖25〗已知两个定点1(4,0)F -,2(4,0)F ,且12MF MF +=6, 则点M 的轨迹方程是________.〖26〗已知,sin sin 2sin A B C +=,若点的坐标分别为.求顶点的轨迹的方程. 〖27〗平面直角坐标系中,过椭圆的右焦点作直交于两点,为的中点,且的斜率为.求的方程.〖28〗已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为(3,0)F ,过点F 的直线交椭圆于,A B 两点.若AB 的中点坐标为(1,1)-,则E 的方程为 ( ) A.2214536x y += B.2213627x y += C.2212718x y += D.221189x y += 〖29〗已知圆221:(1)16F x y ++=，定点2(1,0)F .动圆M 过点2F ，且与圆1F 相内切.求点M 的轨迹C 的方程.ABC ∆,A B (1,0),(1,0)-C W〖30〗一动圆与圆22650x y x +++=外切,同时与圆226910x y x +--=内切,则动圆圆心的轨迹方程为__________________________. 〖31〗已知圆:,圆:,动圆与外切并且与圆内切,圆心的轨迹为曲线 C.求C 的方程.〖32〗一圆形纸片的半径为10cm ，圆心为,O F 为圆内一定点，6OF cm =，M 为圆周上任意一点，把圆纸片折叠，使M 与F 重合，然后抹平纸片， 这样就得到一条折痕CD ，设CD 与OM 交于P 点(如图)， 建立适当的直角坐标系，求点P 的轨迹方程.〖33〗已知O 为坐标原点，点E 、F 的坐标分别为（2-，0）、（2，0），点A 、N 满足23AE =，12ON OA OF =+（），过点N 且垂直于AF 的直线交线段AE 于点M ，设点M 的轨迹为C ．求轨迹C 的方程．〖34〗如图，在平面直角坐标系中，N 为圆A 16)1(:22=++y x 上的一动点，点(1,0)B ，点M 是BN 中点，点P 在线段AN 上，且.0=⋅BN MP 求动点P 的轨迹方程.〖35〗在周长为定值的△ABC 中,已知||6AB =,且当顶点C 位于定点P 时,cos C 有最小值为.建立适当的坐标系,求顶点C 的轨迹方程. 〖36〗在平面直角坐标系中,长度为6的线段PQ 的一个端点P 在射线0(y x =≤0)上滑动,另一端点Q 在射线0(x y =≤0)上滑动,点M 在线段PQ 上,且.21=MQ PM 求点M 的轨迹方程.〖37〗已知点M ,N 分别在直线y mx =和(0)y mx m =->上运动,点P 是线段MN 的中点,且2,MN =动点P 的轨迹是曲线C .求曲线C 的方程,并讨论C 所表示的曲线类型.〖38〗设A ，B 分别是直线255y x =和255y x =-上的两个动点，并且||20AB =，动点P 满足OP OA OB =+．记动点P 的轨迹为C ．求轨迹C 的方程．257〖39〗过两定点)0,(),0,(a A a A -'，)0(>a 分别作两动直线l l ',，此两动直线在y 轴上的截距分别为t t ',，且2b t t ='（b b ,0>为常数）.求两动直线交点的轨迹C 的方程.〖40〗已知椭圆)0(12222>>=+b a by a x 的左、右焦点分别是1(,0)F c -、2(,0)F c ，Q 是椭圆外的动点，满足.2||1a Q F =点P 是线段1F Q 与该椭圆的交 点，点T 在线段2F Q 上，并且满足.0||,022≠=⋅TF TF PT求点T 的轨迹C 的方程．〖41〗在ABC ∆中，已知(0,1)A ，(0,1)B -，,AC BC 两边所在的直线分别与x 轴交于,E F两点，且OF OE ·＝4．求点C 的轨迹方程． 〖42〗θ取一切实数时，连接(4sin ,6cos )A θθ和(4cos ,6sin )B θθ-两点的线段的中点为M ，点M 的轨迹为______________．〖43〗椭圆141622=+y x 上有两点P 、Q ，若O 为原点，斜率41-=⋅OQ OP K K ，求线段PQ 中点M 的轨迹方程。

轨迹问题一、什么是轨迹？轨迹就是目标点的横纵坐标之间的一个等量关系 二、求轨迹的一般方法： 1．直接法：如果动点运动的条件就是一些几何量的等量关系，这些条件简单明确，易于表述成含x,y 的等式，就得到轨迹方程，这种方法称之为直接法。

用直接法求动点轨迹一般有建系,设点，列式，化简，证明五个步骤，最后的证明可以省略，但要注意“挖”与“补”。

2．定义法：运用解析几何中一些常用定义（例如圆锥曲线的定义），可从曲线定义出发直接写出轨迹方程，或从曲线定义出发建立关系式，从而求出轨迹方程。

3.代入法：动点所满足的条件不易表述或求出，但形成轨迹的动点P(x,y)却随另一动点Q(x’，y’)的运动而有规律的运动，且动点Q 的轨迹为给定或容易求得，则可先将x’,y’表示为x,y 的式子，再代入Q 的轨迹方程，然而整理得P 的轨迹方程，代入法也称相关点法。

4.参数法：求轨迹方程有时很难直接找到动点的横坐标、纵坐标之间的关系，则可借助中间变量（参数），使x,y 之间建立起联系，然而再从所求式子中消去参数，得出动点的轨迹方程。

5.交轨法：求两动曲线交点轨迹时，可由方程直接消去参数，例如求两动直线的交点时常用此法，也可以引入参数来建立这些动曲线的联系，然而消去参数得到轨迹方程。

可以说是参数法的一种变种。

6.几何法：利用平面几何或解析几何的知识分析图形性质，发现动点运动规律和动点满足的条件，然而得出动点的轨迹方程。

三、注意事项：1．直接法是基本方法；定义法要充分联想定义、灵活动用定义；化入法要设法找到关系式x’=f(x,y), y’=g(x,y);参数法要合理选取点参、角参、斜率参等参数并学会消参；交轨法要选择参数建立两曲线方程；几何法要挖掘几何属性、找到等量关系。

2．要注意求得轨迹方程的完备性和纯粹性。

在最后的结果出来后，要注意挖去或补上一些点等。

3．求轨迹方程一般只要求出方程即可，求轨迹却不仅要求出方程而且要说明轨迹是什么。

㊀㊀解题技巧与方法㊀㊀１４６㊀关于椭圆切割线轨迹方程的几道题目关于椭圆切割线轨迹方程的几道题目Һ杨光照㊀（陕西省兴平市南位中学，陕西㊀咸阳㊀７１２０００）㊀㊀ʌ摘要ɔ本文试图通过几道题目探求有关椭圆切割线的几何特性，证明过程 大胆猜想，小心求证 ，将抽象的椭圆方程和形象的几何图形联系起来，利于对椭圆几何特性的进一步探索，也有利于解析几何的教授和理解．后面延伸了一道费马大定理三阶题目的证明，采用了微分的思想，强调了抽象思维在求解数学问题中的重要作用．ʌ关键词ɔ椭圆；切割线；轨迹方程；解析几何；费马大定理１．关于椭圆两条互相垂直切线轨迹的论证．已知椭圆ｘ２ａ２＋ｙ２ｂ２＝１（ａ＞ｂ＞０），由椭圆外任意一点Ｑ引椭圆的两条切线，若两条切线互相垂直，求Ｑ点的轨迹．证法１：由满足题设条件的四点Ａ（ａ，ｂ），Ｂ（－ａ，ｂ），Ｃ（－ａ，－ｂ），Ｄ（ａ，－ｂ）共圆，猜想Ｑ点的轨迹为ｘ２＋ｙ２＝ａ２＋ｂ２．原命题转化为从ｘ２＋ｙ２＝ａ２＋ｂ２上任意一点向椭圆引两条切线，若切线垂直，则得证．设ｘ２＋ｙ２＝ａ２＋ｂ２上任意一点Ｍ的坐标为（ｒｃｏｓθ，ｒｓｉｎθ），ｒ＝ａ２＋ｂ２，θ为参数．由Ｍ点向椭圆引一条切线，则切线方程为ｙ－ｒｓｉｎθ＝ｋ（ｘ－ｒｃｏｓθ），得出ｙ＝ｋ（ｘ－ｒｃｏｓθ）＋ｒｓｉｎθ．代入椭圆方程，整理成关于ｘ的一元二次方程，得（ｂ２＋ａ２ｋ２）ｘ２＋２ａ２ｋｒ（ｓｉｎθ－ｋｃｏｓθ）ｘ＋ａ２ｒ２（ｋ２ｃｏｓ２θ＋ｓｉｎ２θ）－ａ２ｒ２ｋｓｉｎ２θ－ａ２ｂ２＝０，由Δ＝０得出关于ｋ的一元二次方程，整理得（ａ２ｓｉｎ２θ－ｂ２ｃｏｓ２θ）ｋ２＋（ａ２＋ｂ２）ｓｉｎ２θｋ＋ｂ２ｃｏｓ２θ－ａ２ｓｉｎ２θ＝０．ȵｋ１㊃ｋ２＝ｂ２ｃｏｓ２θ－ａ２ｓｉｎ２θａ２ｓｉｎ２θ－ｂ２ｃｏｓ２θ＝－１，ʑ两条切线垂直，即证．证法２：由Ｈ（ｍ，ｎ）向椭圆引两条切线，两切点分别为Ａ（ｘ１，ｙ１），Ｂ（ｘ２，ｙ２），则切线方程为ｘ１ｘａ２＋ｙ１ｙｂ２＝１，①㊀ｘ２ｘａ２＋ｙ２ｙｂ２＝１．②由①②式，知ｂ４㊃ｘ１ｘ２ａ４㊃ｙ１ｙ２＝－１，③（斜率乘积＝－１），即ｂ４㊃ｘ１ｘ２＋ａ４㊃ｙ１ｙ２＝０．过这两点的割线方程为ｍｘ１ａ２＋ｎｙ１ｂ２＝１，ｍｘ２ａ２＋ｎｙ２ｂ２＝１，即ｍｘａ２＋ｎｙｂ２＝１．④已知椭圆方程为ｘ２ａ２＋ｙ２ｂ２＝１，⑤由④式得ｙ＝－ｍｂ２ｎａ２ｘ＋ｂ２ｎ，代入⑤，整理成关于ｘ的一元二次方程．可推出ｘ１㊃ｘ２＝ａ４ｂ４－ａ４ｂ２ｎ２ｍ２ｂ４＋ａ２ｂ２ｎ２，同理将ｘ＝－ｎａ２ｍｂ２ｙ＋ａ２ｍ代入⑤，整理得ｙ１㊃ｙ２＝ａ４ｂ４－ａ２ｂ４ｍ２ｎ２ａ４＋ａ２ｂ２ｍ２．把ｘ１㊃ｘ２，ｙ１㊃ｙ２得出的值代入③式，整理得ｍ２＋ｎ２＝ａ２ｂ２，得证．２．已知椭圆ｂ２ｘ２＋ａ２ｙ２＝ａ２㊃ｂ２，一条直线ｌｘ＋ｍｙ＋ｎ＝０和椭圆相交，交点为Ｅ，Ｆ，求证：ＥＯ线段，ＯＦ线段所构成的轨迹方程为ｂ２ｘ２＋ａ２ｙ２＝ａ２㊃ｂ２㊃ｌｘ＋ｍｙｍｎ()２．证明：㊀设ＥＯ线段ｙ＝ｋ１ｘ，ＯＦ线段ｙ＝ｋ２ｘ．则ＥＯ线段，ＯＦ线段的轨迹方程为（ｙ－ｋ１ｘ）㊃（ｙ－ｋ２ｘ）＝ｙ２－（ｋ１＋ｋ２）ｘｙ＋ｋ１ｋ２ｘ２＝０．设Ｅ（ｘ１，ｋ１ｘ１），Ｆ（ｘ２，ｋ２ｘ２）．把Ｅ代入ｌｘ＋ｍｙ＋ｎ＝０，求出ｋ１＝－ｌｘ１＋ｎｍｘ１．同理，Ｆ代入直线，得ｋ２＝－ｌｘ２＋ｎｍｘ２，ｋ１㊃ｋ２＝ｌ２ｘ１ｘ２＋ｎｌ（ｘ１＋ｘ２）＋ｎ２ｍ２ｘ１ｘ２，ｋ１＋ｋ２＝－２ｌｍｘ１ｘ２＋ｎｍ（ｘ１＋ｘ２）ｍ２ｘ１ｘ２éëêêùûúú．把ｌｘ＋ｍｙ＋ｎ＝０整理成ｙ＝－ｌｘ＋ｎｍ，代入椭圆方程，得ｘ１ｘ２＝ａ２ｎ２－ａ２ｂ２ｍ２ｂ２＋ａ２ｌ２，ｘ１＋ｘ２＝－２ａ２ｎｌｍ２ｂ２＋ａ２ｌ２．则可求出ｋ１㊃ｋ２＝ｂ２ｎ２ｍ２－ａ２ｂ２ｌ２ａ２ｎ２ｍ２－ａ２ｂ２ｍ２，ｋ１＋ｋ２＝２ａ２ｂ２ｍｌａ２ｎ２ｍ２－ａ２ｂ２ｍ２，再代入ｙ２－ｋ１＋ｋ２()ｘｙ＋ｋ１ｋ２ｘ２＝０，得ｂ２ｘ２＋ａ２ｙ２＝ａ２ｂ２㊃ｌｘ＋ｍｙｍｎ()２．则轨迹得证．３．关于ｎ３＋ｋ３，即ｎ＋ｋ－（ｘ＋１）＜３ｎ３＋ｋ３＜ｎ＋ｋ－ｘ的论证．考查曲线ｙ＝（ｎ＋ｋ－ｘ）３（ｎȡｋ＞０，ｎ，ｋ，ｘ都是正整数）．取ｘ０ɪｘ，使得ｎ＋ｋ－ｘ０是３ｎ３＋ｋ３所有上限正整数集合中的最小正整数，则有ｎ＋ｋ－ｘ０＋１()[]３ɤｎ３＋ｋ３＜（ｎ＋ｋ－ｘ０）３（ｘ０＜ｋ）．不妨设ｎ３＋ｋ３＝ｎ＋ｋ－（ｘ０＋Δｘ）[]３，则１ȡΔｘ＞０，即０＜Δｘ＜１或Δｘ＝１．若Δｘ＝１，则有ｎ３＋ｋ３＝ｎ＋ｋ－（ｘ０＋Δｘ）[]３＝［ｎ＋ｋ－（ｘ０＋１）］３．因为ｘɤｋ－１，即ｘ＋１ɤｋ，ｎ３＋ｋ３ȡｎ３，故ｋ３ȡ０，则ｋȡ０，与ｋʂ０矛盾．若０＜Δｘ＜１，则ｘ＜ｘ＋Δｘ＜ｘ＋１．故ｎ＋ｋ－（ｘ＋１）[]３＜ｎ＋ｋ－ｘ＋Δｘ()[]３＜ｎ＋ｋ－ｘ()３，故原㊀㊀㊀解题技巧与方法１４７㊀㊀式得证．４．关于三角形内切圆㊁外接圆㊁旁切圆关系的论证．（１）已知әＡＢＣ的内切圆半径为ｒ，外接圆半径为Ｒ，则有Ｒȡ２ｒ，当且仅当Ａ＝Ｂ＝Ｃ＝６０ʎ时，Ｒ＝２ｒ．证明㊀ｒ＝Ｓ－ａ()ｔａｎＡ２＝ａ＋ｂ＋ｃ２－ａ()ｔａｎＡ２＝ｂ＋ｃ－ａ２㊃ｔａｎＡ２＝２ＲｓｉｎＢ＋２ＲｓｉｎＣ－２ＲｓｉｎＡ２㊃ｔａｎＡ２＝ＲｓｉｎＢ＋ｓｉｎＣ－ｓｉｎＡ()ｔａｎＡ２＝Ｒ２ｓｉｎＢ＋Ｃ２ｃｏｓＢ－Ｃ２－ｓｉｎＡ()ｔａｎＡ２＝Ｒ２ｃｏｓＡ２ｃｏｓＢ－Ｃ２－ｓｉｎＡ()ｔａｎＡ２ɤＲ２ｃｏｓＡ２－２ｓｉｎＡ２ｃｏｓＡ２()ｔａｎＡ２＝２ＲｃｏｓＡ２１－ｓｉｎＡ２()ｔａｎＡ２＝２ＲｓｉｎＡ２１－ｓｉｎＡ２()ɤ２ＲｓｉｎＡ２＋１－ｓｉｎＡ２()２éëêêêùûúúú２＝１２Ｒ，取等号的条件为Ａ＝Ｂ＝Ｃ＝６０ʎ，得证．（２）已知әＡＢＣ的内切圆半径为ｒ，外接圆半径为Ｒ，ＢＣ边上的旁切圆半径为ｒａ，若øＡȡøＢȡøＣ，则有ｒａȡ３２Ｒȡ３ｒ，当且仅当Ａ＝Ｂ＝Ｃ时，等号成立．证明㊀设ＢＣ边上的旁切圆的圆心为Ｏ３，与边ＢＣ的切点为Ｈ，则有ＳәＢＯ３Ｃ＝２ＲｓｉｎＡ()２ｓｉｎπ－Ｂ２()ｓｉｎπ－Ｃ２()２ｓｉｎπ－Ｂ＋Ｃ２()＝２Ｒ２ｓｉｎ２ＡｃｏｓＢ２ｃｏｓＣ２ｃｏｓＡ２，①ＳәＢＯ３Ｃ＝１２ＢＣ㊃Ｏ３Ｈ＝１２㊃２ＲｓｉｎＡ㊃ｒａ＝ＲｓｉｎＡ㊃ｒａ．②①②联立，则有ｒａ＝２ＲｓｉｎＡｃｏｓＢ２ｃｏｓＣ２ｃｏｓＡ２＝４ＲｓｉｎＡ２ｃｏｓＢ２ｃｏｓＣ２＝２ｓｉｎＡ２ｃｏｓＢ２()２ＲｃｏｓＣ２＝ｓｉｎＡ＋Ｂ２＋ｓｉｎＡ－Ｂ２()２ＲｃｏｓＣ２＝ｃｏｓＣ２＋ｓｉｎＡ－Ｂ２()２ＲｃｏｓＣ２＝２Ｒｃｏｓ２Ｃ２＋２ＲｃｏｓＣ２ｓｉｎＡ－Ｂ２ȡ２Ｒｃｏｓ２Ｃ２．ȵøＣɤ６０ʎ，ｃｏｓＣ２ȡ３２，ʑｒａȡ２Ｒｃｏｓ２Ｃ２ȡ３２Ｒȡ３ｒ，当且仅当Ａ＝Ｂ＝Ｃ时，等号成立．（３）已知әＡＢＣ的内切圆半径为ｒ，外接圆半径为Ｒ，ＢＣ边上的旁切圆半径为ｒａ，若øＡɤøＢɤøＣ，则有３ｒɤｒａɤ３２Ｒ，当且仅当Ａ＝Ｂ＝Ｃ时，等号成立．证明㊀ｒａ＝４ＲｓｉｎＡ２ｃｏｓＢ２ｃｏｓＣ２＝２ＲｓｉｎＡ２２ｃｏｓＢ２ｃｏｓＣ２()＝２ＲｓｉｎＡ２ｃｏｓＢ＋Ｃ２＋ｃｏｓＢ－Ｃ２()＝２ＲｓｉｎＡ２ｓｉｎＡ２＋ｃｏｓＢ－Ｃ２()＝２Ｒｓｉｎ２Ａ２＋２ＲｓｉｎＡ２ｃｏｓＢ－Ｃ２．ȵøＡɤ６０ʎ，ｓｉｎＡ２ɤ１２且ｃｏｓＢ－Ｃ２ɤ１，ʑｒａɤＲ２＋Ｒ＝３２Ｒ．又ȵｒｒａ＝ｃｏｓＢ－Ｃ２－ｃｏｓＢ＋Ｃ２ｃｏｓＢ－Ｃ２＋ｃｏｓＢ＋Ｃ２ɤ１－ｃｏｓＢ＋Ｃ２１＋ｃｏｓＢ＋Ｃ２＝１－２ｃｏｓＢ＋Ｃ２１＋ｃｏｓＢ＋Ｃ２＝１－２１ｃｏｓＢ＋Ｃ２＋１ɤ１－２１１２＋１＝１３，ʑ３ｒɤｒａɤ３２Ｒ，当且仅当Ａ＝Ｂ＝Ｃ时，等号成立．ʌ参考文献ɔ［１］玉云化．椭圆㊁双曲线与相关圆生成的轨迹方程［Ｊ］．数学通讯：教师阅读，２０１２（０１）：３７－４０．［２］饶志明．与椭圆切线相关的定值定点定直线问题［Ｊ］．中学数学教学参考：上旬，２０１６（１５）：３１－３２．［３］许少华．椭圆标准方程的求法［Ｊ］．数理天地：高中版，２０１１（０６）：１４－１５．。

龙源期刊网
例谈物理问题中的“椭圆”
作者：付尊来李兴
来源：《中学物理·高中》2013年第12期
椭圆是高中数学中的重点章节之一，也是高考数学考查的重点内容.其实在许多物理问题
中也不乏有椭圆的身影，椭圆知识在解决这类物理问题时往往有着重要的应用，现举几例加以说明，供读者赏析.
例1从距离地面高为h的A点在同一竖直平面内以恒定的速率v0斜上抛一小球，不计空气阻力，初速度方向与水平方向的夹角为θ，当θ取不同数值时，小球在运动过程中最高点的位置是不同的.试证明最高点的轨迹连线为一椭圆.
解析由动力学知识可知，小球在水平方向上做匀速直线运动，竖直方向上做竖直上抛运动.如图1所示，选抛出点A为坐标原点建立平面直角坐标系，D为最高点.当小球竖直向上的分速度减小到零时，小球上升到最高点.
本例是利用椭圆相关知识求解动点轨迹的典范，对培养和提高学生应用数学工具解决物理问题的能力大有裨益.
导数和微分早已列入高中数学教学大纲，本例中如果不具备一定的椭圆知识和运算能力，要想完成速度表达式的求解几乎是不可能的.
本例巧妙的证明了小球的运动轨迹为一椭圆，然后通过求导运算得出轨迹上任意一点切线斜率的表达式，进而求得小球在某一位置对地的速度方向，并使得系统水平方向动量守恒定律的方程得以顺利建立，为最终解决本题扫清了关键障碍，堪称是椭圆知识与物理规律应用的典范.
以上三个例题都从不同的角度首先准确的描述出物体运动的轨迹方程，然后利用相关椭圆知识和物理规律，并最终使问题得以完美解决，充分体现了数学与物理的结合之美.。

而h ′1()x =12x，h ′2()x =-2x .由h ′1()x 0=h ′2()x 0得-12x 20=-2x 0，解得x 0，y 0=，所以p èø，则m =èø2+.画出h 1()x=12x和h 2()x =-x 2+m 的图象，如图1、2、3所示.由图可知，当m时，两个函数图象有1个交点；当m =时，两个函数图象有2个交点；当m 时，两个函数图象有3个交点.即当m >时，方程有1个根；当m =时，方程有2个根；当m 时，方程有3个根.将原方程解的个数转化为两个函数h 1()x =12x和h 2()x =-x 2+m 的交点的个数.而两个函数一定一动，确定两个函数图象相切时的位置，便可确定两个函数图象交点的个数.利用导数的几何意义便可求得切点的坐标，进而得到两图象相切时m 的取值.函数、方程之间的联系紧密.在解答含参方程问题时，我们要注意将问题转化为函数问题来求解，利用导数法、函数的图象来分析、解答问题.这样不仅能拓宽解题的思路，还能有效地提升解题的效率.(作者单位:江西省赣州市赣县中学)图1图2图3求解圆锥曲线轨迹问题的方法有很多，比如定义法、直接法、相关点法（或叫代入法）、参数法等.对于与椭圆有关的轨迹问题，我们也同样可以运用这些方法来求解.其中定义法是应用范围最广、使用频率最高的一种方法.而椭圆的定义有三种:第一、二、三定义,本文重点探讨如何运用椭圆的这三个定义来求解与椭圆有关的轨迹问题.一、椭圆的第一定义椭圆的第一定义：平面内与两个定点F 1,F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹.这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距.在求解与椭圆有关的轨迹问题时，我们可以直接套用椭圆的第一定义，寻找动点到两定点的距离之和，然后建立关系式,即∣F 1F 2∣=2c ,|PF 1|+|PF 2|=2a ,得到椭圆的焦距、长轴长，进而求得曲线的轨迹方程.例1.已知椭圆C ：x 2a 2+y 2b2=1(a >b >0)，M 为椭圆上的一个动点，F 1为椭圆的左焦点，则线段MF 1的中点P 的轨迹是（）.A.圆B.椭圆C.双曲线D.抛物线解析：不妨设椭圆C 的右焦点为F 2，根据椭圆的第一定义不难得到：|PF 1|+|PO |=12(|MF 1|+|MF 2|)=a >c ,根据椭圆的第一定义可知点P 的轨迹是椭圆.解：设椭圆C 的右焦点为F 2，坐标原点为O ，由椭圆的定义得|MF 1|+|MF 2|=2a >2c ，则|PF 1|+|PO |=12(|MF 1|+|MF 2|)=a >c ，则点P 的轨迹是以F 1、O 为焦点的椭圆，故本题答案为B 项.二、椭圆的第二定义圆锥曲线的第二定义：到定点的距离与到定直线的距离的比是e 的点的轨迹，其中定点为焦点，定直线为准线.当0<e <1时该曲线为椭圆；当e =1时该曲线为抛物线；当e >1时该曲线为双曲线.椭圆的第二朱园娇章长红解题宝典39解题宝典定义将焦半径的长度转化为到准线的距离，突出曲线上动点的横坐标.在解题时，我们只需要明确准线的位置和椭圆上的动点的横坐标，便可使问题得解.例2.已知点P 是正四面体V -ABC 侧面VBC 上一点，且点P 到底面ABC 的距离与它到顶点V 的距离相等，则动点P 的轨迹（）.A.线段B.圆的一部分C.椭圆的一部分D.双曲线的一部分解：过P 作PD ⊥平面ABC 于D ，过D 作DH ⊥BC 于H ，连接PH ，如图1，由题意可得BC ⊥平面DPH ，所以BC ⊥PH ，故∠PHD 为二面角V -BC -A 的平面角，令其为α，则在Rt△PDH 中，||PD :||PH =sin α，又点P 到平面ABC 距离与到点V 的距离相等，即||PV =||PD ，所以||PV :||PH =sin α<1，所以在平面VBC 中，点P 到点V 的距离与到直线BC 的距离之比为sin α<1，由椭圆的第二定义知P 点的轨迹为椭圆在平面VBC 内的一部分．解答这个题目的关键是作出并求得点P 到底面的距离.通过添加辅助线，设二面角V -BC -A 为α，由二面角的定义可得点P 到点V 的距离与定直线BC 的距离之比为一个常数，根据椭圆的第二定义即可得到问题的答案.三、椭圆的第三定义椭圆的第三定义也叫椭圆的斜率积定义，是指平面内动点到两定点A 1(a ,0)和A 2(-a ,0)的斜率的乘积等于常数e 2-1的点的轨迹.其中两定点为椭圆的顶点.椭圆的第三定义将斜率的乘积作为主要关系，那么我们在解题时可以根据斜率的这种关系来进行求解.例3.设P 为椭圆C :x 2a 2+y 2b2=1(a >b >0)上的动点，F 1,F 2为椭圆的两个焦点，I 为△PF 1F 2的内心，求点I的轨迹方程．解析：由于本题是与焦点三角形的内切圆有关的问题，所以要依据分割图形的面积来寻找圆的半径和三角形三边之间的关系.由内心I 是动点，F 1和F 2是两个定点，我们可联想到椭圆的第三定义，结合这两个关系式得到IF 1与IF 2的斜率之积是一常数，根据椭圆的第三定义就不难发现并求得点I 的轨迹方程.解：如图2，设内切圆I 与F 1F 2的切点为H ，半径为r ，且设F 1H =y ，F 2H =z ,PF 1=x +y ,PF 2=x +z ,c =a 2+b 2，则{y +z =2c ,2x +y +z =2a ,所以直线IF 1与IF 2的斜率之积为k IF 1∙k IF 2=-IH 2F 1H ∙F 2H=-r 2yz ，而根据海伦公式可得△PF 1F 2的面积为()x +y +z r =xyz ()x +y +z ，因此k IF 1∙k IF 2=-x x +y +z =-a -ca +c .根据椭圆的斜率积定义可得I 点的轨迹是以F 1F 2为长轴，离心率为e 的椭圆，其标准方程为x 2c 2+y 2a -c a +c∙c 2=1()y ≠0.我们知道，椭圆中有个重要的结论：椭圆x 2a 2+y 2b2=1(a >b >0)上任意一点到椭圆长轴的两个端点的斜率之积等于-b2a2.椭圆的第三定义是这个结论的逆命题.因此，对于椭圆中与角度、斜率有关的问题，我们都可以利用椭圆的第三定义，根据椭圆中与角度、斜率建立关系式，求得椭圆的方程.以上三个题目分别借助椭圆的第一定义、第二定义、第三定义求解与椭圆有关的轨迹问题.在解题过程中，我们要学会依据题意，结合图形，紧扣椭圆的三个定义对题目中的条件进行转化，比如，例1是根据椭圆的第一定义将中位线转化为动点到两定点的距离之和，例2是根据椭圆的第二定义，将点P 到平面ABC 距离与到点V 的距离之间的关系转化为点P 到点V 的距离与到直线BC 的距离之比，例3是根据椭圆的第三定义，将圆的半径和三角形三边之间的关系转化为k IF 1∙k IF 2.通过转化便可建立动点满足的等量关系式，联系椭圆的定义，从而达到解答与椭圆有关的轨迹问题的目的.(作者单位:江西省余干第一中学)图1图240。

与椭圆有关的轨迹方程的求法一.定义法：若动点轨迹的条件符合某一基本轨迹的定义，可用定义直接探求.例1：已知两圆169)4(:221=+-y x C ，9)4(:221=++y x C ，动圆在圆1C 内部且和圆1C 相内切，和圆2C 相外切，求动圆圆心M 的轨迹方程.分析：动圆满足的条件为：①与圆C 1相内切；②与圆C 2相外切．依据两圆相切的充要条件建立关系式 解：设动圆圆心),(y x M ，半径为r 如图所示，由题意:圆Ｍ内切于圆C 1，∴r MC -=131， 圆Ｍ外切于圆C 2 ，∴r MC +=32， ∴1621=+MC MC ,∴动圆圆心Ｍ的轨迹是以C 1、C 2为焦点的椭圆， 且82,162==c a ，48222=-=c a b ，故所求轨迹方程为：1486422=+y x 。

例2．在周长为定值的ABC ∆中,已知|AB |6=，且当顶点C 位于定点P 时,C cos 有最小值为257，建立适当的坐标系，求顶点C 的轨迹方程. 解：以AB 所在直线为x 轴，线段AB 的中垂线为y 轴建立直角坐标系,设 )3(2>=+a a CB CA 为定值，则C 点的轨迹是以B A ,为焦点的椭圆， 焦距62==AB c ，因为：1||||182||||236||||2|)||(|||||26||||cos 22222--=--+=-+=CB CA a CB CA CB CA CB CA CB CA CB CA C又 22)22(||||a a CB CA =≤⋅，所以 2181cos a C -≥， 由题意得 25,25718122==-a a，此时，PB PA =，P 点坐标为)4,0(±， 所以C 点的轨迹方程为：)0(1162522≠=+y y x 。

例3．已知圆16)1(:22=++y x B 及点)0,1(A ，C 为圆B 上任一点，求线段AC 的垂直平分线l 与线段BC 交点P 的轨迹方程。

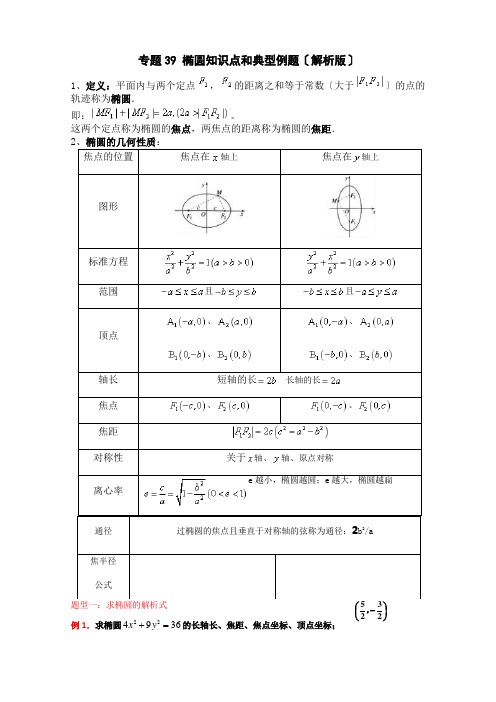
专题39 椭圆知识点和典型例题〔解析版〕1、定义：平面内与两个定点，的距离之和等于常数〔大于〕的点的轨迹称为椭圆．即：。

这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距． 2、椭圆的几何性质：焦点的位置 焦点在轴上焦点在轴上 图形标准方程 范围且 且 顶点、、、、轴长 短轴的长长轴的长焦点 、、焦距对称性 关于轴、轴、原点对称离心率e 越小，椭圆越圆；e 越大，椭圆越扁题型一：求椭圆的解析式例1．求椭圆224936x y +=的长轴长、焦距、焦点坐标、顶点坐标；通径 过椭圆的焦点且垂直于对称轴的弦称为通径：2b 2/a焦半径公式⎪⎭⎫ ⎝⎛-2325，【详解】椭圆224936x y +=化为标准方程22194x y +=，∴3a =，2b =，∴c ==∴椭圆的长轴长为26a =，焦距为2c =焦点坐标为()1F，)2F ，顶点坐标为()13,0A -，()23,0A ，()10,2B -，()20,2B . 例2．求适合以下条件的椭圆标准方程：〔1〕与椭圆2212x y +=有相同的焦点，且经过点3(1,)2〔2〕经过(2,(22A B 两点 【详解】〔1〕椭圆2212x y +=的焦点坐标为(1,0)±，∵椭圆过点3(1,)2，∴24a =，∴2,a b ==，∴椭圆的标准方程为22143x y +=.〔2〕设所求的椭圆方程为221(0,0,)x y m n m n m n+=>>≠．把(2,(A B 两点代入， 得：14213241mnm n⎧⎪+=⎪⎪⎨⎪⎪+=⎪⎩，解得81m n ==，， ∴椭圆方程为2218x y +=．题型二：求轨迹例3．在同一平面直角坐标系xOy 中，圆224x y +=经过伸缩变换:12x x y y ϕ=⎧⎪⎨=''⎪⎩后，得到曲线C .求曲线C 的方程； 【详解】设圆224x y +=上任意一点(),M x y 经过伸缩变换:12x xy y ω=⎧⎪⎨=''⎪⎩得到对应点(),M x y '''.将x x '=，2y y '=代入224x y +=，得()2224x y ''+=，化简得2214x y ''+=.∴曲线C 的方程为2214x y +=；例4．ABC 中，角、、A B C 所对的边分别为,>>、、a b c a c b ，且2,2=+=c a b c ，求点C 的轨迹方程． 【详解】由题意，以AB 所在直线为x 轴，线段AB 的垂直平分线为y 轴建立平面直角坐标系， 如下图，因为2c =，那么(1,0),(1,0)A B -，设(,)C x y ， 因为2a b c +=，即||||2||CB CA AB +=，4=，整理得所以22143x y +=，因为a b >，即||||CB CA >，所以点C 只能在y 轴的左边，即0x <． 又ABC 的三个顶点不能共线，所以点C 不能在x 轴上，即2x ≠-．所以所求点C 的轨迹方程为221(20)43x y x +=-<<．例5在圆228x y +=上任取一点P ，过P 作x 轴的垂线PD ，D 为垂足.当点P 在圆上运动时，求线段PD 的中点Q 的轨迹方程. 【详解】解：在圆228x y +=上任取一点P ，过P 作x 轴的垂线PD ，D 为垂足，设0(P x ，0)y ，(,)M x y ，0(D x ，0)，M 是PD 的中点，0x x ∴=，02y y =，又P 在圆228x y +=上，22008x y ∴+=，即2248x y +=，∴22182x y +=，∴线段PD 的中点M 的轨迹方程是22182x y +=.题型三：求参数的范围例6：椭圆2222:1(0)y x C a b a b+=>>的上下两个焦点分别为12,F F ，过点1F 与y 轴垂直的直线交椭圆C 于 ,M N 两点，2MNF ∆C 〔1〕求椭圆C 的标准方程；〔2〕O 为坐标原点，直线:l y kx m =+与y 轴交于点P ，与椭圆C 交于,A B 两个不同的点，假设存在实数λ，使得4OA OB OP λ+=，求m 的取值范围.由题意2MNF ∆的面积为21212||2b cF F MN c MN a===由得c a =21b =，∴24a =， ∴椭圆C 的标准方程为2214y x +=．〔Ⅱ〕假设0m =，那么()0,0P ，由椭圆的对称性得AP PB =，即0OA OB +=， ∴0m =能使4OA OB OP λ+=成立． 假设0m ≠，由4OA OB OP λ+=，得144OP OA OB λ=+， 因为A ，B ，P 共线，所以14λ+=，解得3λ=．设()11,A x kx m +，()22,B x kx m +，由22,{440,y kx m x y =++-=得()2224240k x mkx m +++-=，由得()()222244440m k k m ∆=-+->，即2240k m -+>，且12224km x x k -+=+，212244m x x k -=+，由3AP PB =，得123x x -=，即123x x =-，∴()21212340x x x x ++=， ∴()()2222224412044m k m k k-+=++，即222240m k m k +--=．当21m =时，222240m k m k +--=不成立，∴22241m k m -=-，∵2240k m -+>，∴2224401m m m --+>-，即()222401m m m ->-， ∴214m <<，解得21m -<<-或12m <<．综上所述，m 的取值范围为{|21012}m m m m -<<-=<<或或．直线与圆锥曲线的位置关系2.直线与圆锥曲线的位置关系： ⑴.从几何角度看：〔特别注意〕要特别注意当直线与双曲线的渐进线平行时，直线与双曲线只有一个交点；当直线与抛物线的对称轴平行或重合时，直线与抛物线也只有一个交点。

椭圆的基本知识1．椭圆的定义：把平面内与两个定点21,F F 的距离之和等于常数（大于21F F ）的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点，两焦点的距离叫做焦距(设为2c ) . 2.椭圆的标准方程：12222=+b y a x （a ＞b ＞0） 12222=+bx a y （a ＞b ＞0） 焦点在坐标轴上的椭圆标准方程有两种情形，为了计算简便，可设方程为mx2+ny2=1(m>0，n>0)不必考虑焦点位置，求出方程3.求轨迹方程的方法: 定义法、待定系数法、相关点法、直接法.,.2,,1的轨迹中点求线段段轴作垂线向从这个圆上任意一点半径为标原点已知一个圆的圆心为坐如图例M P P P P x P ''解:(相关点法)设点M (x , y ),点P (x 0, y 0),则x ＝x 0, y ＝2y 得x 0＝x ， y 0＝2y. ∵x 02＋y 02＝4, 得 x 2＋(2y )2＝4,即.142=+y x所以点M 的轨迹是一个椭圆.4.范围. x 2≤a 2，y 2≤b 2，∴|x|≤a ，|y|≤b ． 椭圆位于直线x ＝±a 和y ＝±b 围成的矩形里．yO F 1F 2xMc c xF 2F 1O y Mcc yxPO P 'M5.椭圆的对称性椭圆是关于y 轴、x 轴、原点都是对称的．坐标轴是椭圆的对称轴． 原点是椭圆的对称中心．椭圆的对称中心叫做椭圆的中心．6.顶点 只须令x ＝0，得y ＝±b ，点B 1(0,－b )、B 2(0, b )是椭圆和y 轴的两个交点；令y ＝0，得x ＝±a ，点A 1(－a ,0)、A 2(a ,0)是椭圆和x 轴的两个交点．椭圆有四个顶点：A 1(－a , 0)、A 2(a , 0)、B 1(0, －b )、B 2(0, b )．椭圆和它的对称轴的四个交点叫椭圆的顶点．线段A 1A 2、B 1B 2分别叫做椭圆的长轴和短轴. 长轴的长等于2a . 短轴的长等于2b .a 叫做椭圆的 长半轴长．b 叫做椭圆的短半轴长． |B 1F 1|＝|B 1F 2|＝|B 2F 1|＝|B 2F 2|＝a ． 在Rt△OB 2F 2中，|OF 2|2＝|B 2F 2|2－|OB 2|2， 即c 2＝a 2－b 2．7.椭圆的几何性质：椭圆的几何性质可分为两类：一类是与坐标系有关的性质，如顶点、焦点、中心坐标；一类是与坐标系无关的本身固有性质，如长、短轴长、焦距、离心率．对于第一类性质，只要2222x y 1(a b 0)a b +=>>的有关性质中横坐标x 和纵坐标y 互换，就可以得出2222y x 1(a b 0)a b+=>>的有关性质。

椭圆内一点与椭圆上一点连线中点的轨迹方程首先，让我们来研究椭圆内一点与椭圆上一点连线中点的轨迹方程。

在解决这个问题之前，让我们先了解一下椭圆的基本性质。

椭圆是一个平面内到两个固定点（焦点）的距离之和等于常数的点的集合。

这两个固定点被称为焦点，椭圆上到两个焦点距离之和等于2a，a为长半轴的长度。

此外，椭圆的中心到焦点的距离称为焦距，记为c。

椭圆的方程通常写为：\(\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1\)其中，(h, k)为椭圆的中心坐标，a为长半轴的长度，b为短半轴的长度。

现在，我们来解决椭圆内一点与椭圆上一点连线中点的轨迹方程。

设椭圆的方程为\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\)，其中a>b>0。

我们将椭圆上一点的坐标设为(x1, y1)，椭圆内一点的坐标设为(x2, y2)，连线中点的坐标设为(xm, ym)。

根据中点的定义，我们知道中点的坐标为\((\frac{x1 + x2}{2}, \frac{y1 +y2}{2})\)。

我们的目标是找出椭圆内一点与椭圆上一点连线中点的轨迹方程。

为了简化问题，我们假设椭圆的中心为原点(0, 0)。

椭圆上一点的坐标为(x1,y1)，根据椭圆的方程，我们可以得到\(x1 = a \cdot \cos(\theta)\)和\(y1 = b \cdot\sin(\theta)\)，其中θ为椭圆上一点的极坐标角度。

现在，我们考虑椭圆内一点的坐标为(x2, y2)，根据椭圆的方程，我们可以得到\(\frac{x2^2}{a^2} + \frac{y2^2}{b^2} = 1\)。

设椭圆内一点的极坐标为(ρ, φ)，其中ρ为椭圆内一点到原点的距离，φ为椭圆内一点的极坐标角度。

根据极坐标的性质，我们可以得到\(x2 = \rho \cdot \cos(\phi)\)和\(y2 = \rho \cdot \sin(\phi)\)。

椭圆焦点三角形重心轨迹方程哎呀，今天我们来聊聊椭圆焦点三角形重心轨迹方程。

听起来好像很高深对吧？其实说白了，就是在搞数学的那些事儿。

先想象一下，椭圆就像个悠闲的橄榄球，圆润又优雅。

而焦点嘛，就像是椭圆身上的两颗小星星，永远不离不弃，互相牵挂。

你有没有想过，咱们在椭圆上画个三角形，然后这个三角形的重心会在哪里移动呢？想象一下，三角形的三个顶点在椭圆上跳舞，每次跳舞的位置都在变动。

可是啊，不管怎么跳，三角形的重心就像一个勤劳的小蜜蜂，总是要找到一个最稳的地方。

这个地方就是重心的轨迹，哎呀，真有趣。

就像我们生活中一样，尽管周围变化无常，但总有一些东西是稳固的，对吧？咱们把这个重心轨迹方程搞清楚，就像找到一条通向快乐的路。

说到这里，有点数学术语了。

重心的计算其实很简单，三个顶点的坐标加起来除以三，听起来是不是简单得让人想笑？所以无论椭圆怎么变，重心却是一个值得信赖的小伙伴。

它的轨迹就像一个稳重的老大爷，无论发生什么，都能保持自己的步伐。

再聊聊椭圆焦点的那些事儿。

大家都知道，椭圆的焦点有两个，感觉就像是一对情侣，互相吸引，又不太会相互碰撞。

椭圆的方程也许让人眼花缭乱，但只要记住它的基本特性，你就能玩得飞起。

它的形状、大小都可以随意调整，像一个调皮的小孩，想怎么来就怎么来。

三角形的重心呢，随着椭圆的变化，也会发生变化。

就像是一个旅行者，在不同的地方留下自己的足迹。

这个过程让人想到人生的旅程，我们在不同的阶段会遇到不同的挑战，但重心总能让我们找到自己的方向。

每一次调整，每一次变化，都是在为自己的人生添砖加瓦。

最终重心的轨迹方程又是什么呢？说实话，搞清楚这一点并不复杂。

只要懂得椭圆的基本性质，你就能轻松地推导出重心的轨迹。

数学就像一位耐心的老师，愿意慢慢引导你走向更高的山峰。

每一个方程背后都有一段故事，等待着你去发掘。

在生活中，其实我们也可以像这个重心一样，寻找属于自己的稳定感。

无论外界如何喧嚣，总有一个点可以让我们安心。

椭圆的平行弦中点的轨迹方程可以通过以下步骤推导得到：
设椭圆的标准方程为：(x-h)²/a² + (y-k)²/b² = 1，其中(h, k) 是椭圆的中心坐标，a 和b 分别是椭圆的半长轴和半短轴的长度。

现在考虑椭圆上的两个平行弦的斜率分别为m1 和m2。

我们要求这两条平行弦的中点的轨迹方程。

对于一条平行弦，设其方程为y = m1x + c1，其中c1 是常数。

在椭圆上，代入椭圆方程可得：(x-h)²/a² + (m1x + c1 - k)²/b² = 1。

整理后可得：(b²+a²m1²)x² + 2a²m1(c1-k)x + a²(c1-k)² - a²b² = 0。

这是一个关于x 的二次方程，其系数分别为(b²+a²m1²)，2a²m1(c1-k)，和a²(c1-k)² - a²b²。

根据二次方程的性质，该方程的根是x 的函数，可以用一条曲线来表示。

因此，椭圆上的一条平行弦的中点的轨迹方程是该二次方程的根的轨迹方程。

同理，对于另一条平行弦，其方程为y = m2x + c2，其中c2 是常数。

代入椭圆方程并整理可得类似的二次方程。

综上所述，椭圆的平行弦中点的轨迹方程是两个二次方程的根的轨迹方程。

具体的方程形式将取决于给定的斜率m1 和m2。

请注意，由于计算较为复杂，具体的轨迹方程可能需要进行进一步化简或使用数值方法来求解。