职高数学5.3任意角的正弦函数、余弦函数和正切函数

任意角的正弦函数、余弦函数和正切函数的概念佛山市顺德区郑敬诒职业技术学校黎玉珊【百度搜索】/view/b6c426c8a1c7aa00b52acbc6.html【百度搜索】/view/001d2e1ea300a6c30c229f72.html【百度搜索】/view/71d5f475f46527d3240ce03f.html【百度搜索】/view/13a30ad628ea81c758f5782e.html【百度搜索】/view/a16a75084a7302768e9939a6.html【课内教学】（一）复习引入、回想再认。

问题：初中，我们学习过锐角三角函数，（如图1）在OMP Rt ∆中，M ∠是直角，那么根据锐角三角函数的定义，O ∠的正弦、余弦和正切是如何定义的？（通过提问，帮助学生回顾初中学过的锐角三角函数的定义）xy OM PM r x OP OM r y OP PM ======|||tan |||cos ||||sin ｜＝邻边对边｜＝斜边邻边＝斜边对边ααα 教师强调：只要角度确定了，无论角的边长如何改变，正弦、余弦和正切值都已经确定了。

每一个确定的锐角，都有相应的唯一的正弦值、余弦值和正切值与之对应。

因此，锐角三角函数是以角为自变量，以边长的比值为函数值的函数。

（以此强调来唤醒学生函数的认识）（二） 探讨学习、建构知识。

上节课，我们已经把锐角推广到了任意角，今天锐角的三角函数概念也能推广到任意角吗？试试看，可以独立思考和探索，也可以互相讨论！问题1：今天我们能否继续在直角三角形中定义任意角的三角函数？（引导学生在平面直角坐标系中定义任意角三角函数）问题2：（追问）在上节课，我们是如何将锐角的概念推广到任意角的？（更进一步引导学生在平面直角坐标系中定义任意角三角函数）打开【百度搜索】/view/be293d619b6648d7c1c746fb.html 网络上课件，与学生一起探讨将锐角三角形放到直角坐标系中研究（如图2）：把锐角α放置于直角坐标系（角的顶点与原点重合，角的始边与x 轴非负轴重合），在直角坐标系中，在角α终边上任取一点p ，作x PM ⊥轴于M ，构造一个OMP RT ∆，则α=∠MOP （锐角）设)0,0)(,(>>b a b a P ，α的邻边a OM =、对边b MP =，斜长 22||b a r OP +== 图2α图4 问题3：我们知道，借助平面直角坐标系，就可以将几何问题代数化，如将点用坐标表示出来，把线段的长用坐标算出来。

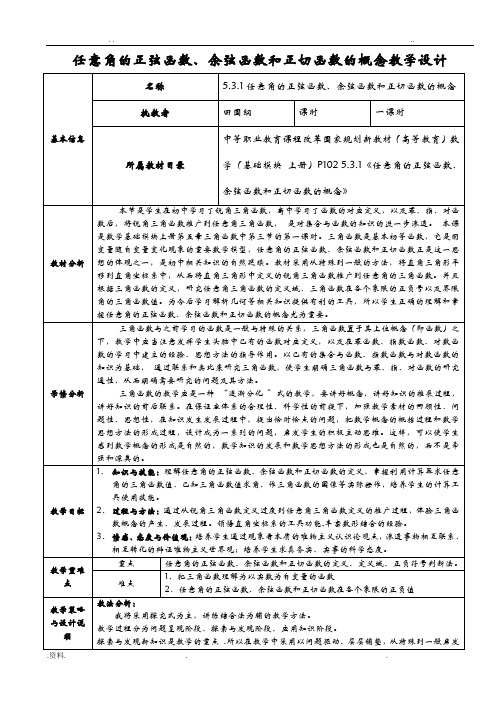
任意角的正弦函数、余弦函数和正切函数的概念教学设计打开【百度搜索】：wenku.baidu./view/be293d619b6648d7c1c746fb.html网络上课件把锐角α放置于直角坐标系（角的顶点与原点重合，角的始边与x轴非负轴重合），在直角坐标系中，在角α终边上任取一点B，作xBE⊥轴于E，构造一个OEBRT∆，则α=∠EOB（锐角）设)0,0)(,(>>babaB，α的邻边aOE=、对边bEB=，斜长22||barOB+==问题3：我们知道，借助平面直角坐标系，就可以将几何问题代数化，如将点用坐标表示出来，把线段的长用坐标算出来。

那我们能否在平面直角坐标系中，用角的终边上的点的坐标学生一起探讨将锐角三角形放到直角坐标系中研究（如图2）自主学习，集体探究么角α的正弦、余弦和正切分别定义为：正弦：r y=αsin余弦：r x=αcos 正切：x y =αtan为使学生更深刻领会任意角三角函数的定义，引导学生思考如下两个问题：问题5：比值会随着点B 在终边的位置改变而改变吗？打开《math3d 6.09》（如图3），这样的处理，不仅保持了学生一定的思考能力，还有助于学生克服认识上的困难，既用坐标定义了三角函数，又解决了在直角三角形中不能定义任意角的三角函数的问题，并形成正确的认识培养过程思维，联系相似三角形知识，探索发现，得出“对于角α的每一个确定值，三个比值都是确定的，不会随B在终边上的移动而变化”。

问题6：角α大小发生变化时，比值会改变吗？打开《math3d 6.09》动画演示（如图4）。

观察，体验先由学生自由发表意见学生观察三角函数值的变化强化函数两个变量之间的变化关系培养个性思维通《math3d6.09》的动态演示，使本节课学习的重点得到更好的理解，也可以帮助学生突破难点。

图4。

5.3《任意角的正弦函数、余弦函数和正切函数》教案授课题目任意角的正弦函数、余弦函数和正切函数授课课时3课型讲授教学目标1.知识与能力（1）能够运用公式求解任意角的三角函数值；（2）掌握三角函数的表达式；（3）正确判断任意角的三角函数值的符号.2. 过程与方法观察、分析知识形成的过程，归纳、抽象、概括知识的概念，提升寻找数学规律的能力.3. 情感、态度与价值观（1）感知数学知识与实际生活的普遍联系；（2）享受积极交流的课堂气氛，增强学习的兴趣和勇于创新的精神.教学重难点重点：任意角的三角函数值；难点：三角函数值的符号.第1课时教学过程教学活动学生活动设计思路复习引入在初中，我们在直角△ABC中，我们定义了锐角α的正弦、余弦和正切，如图1所示.正弦：asincαα∠==的对边斜边；图1余弦：cos b c αα∠==的邻边斜边；正切：tan a b ααα∠==∠的对边的邻边.现在我们将一个锐角α放入平面直角坐标系中，使得顶点与原点重合， 始边与x 轴的非负半轴重合，如图2所示.已知点(,)P x y 是锐角α终边上的任意一点，点P 与原点O 的距离(0)OP r r =>，你能利用锐角三角函数的定义计算出锐角α所对应的三角函数值吗？分析 过点P 作x 轴的垂线，垂足为M ，则线段OM 的长度为x ，线段MP 的长度为y .在Rt OMP ∆中，根据勾股定理可得，222r x y =+，即220r x y =+>.MP sin y OP r α==；OM cos xOP r α==； MP tan yOM xα==.一、探究新知在弧度制下，我们已将α的范围扩展到了全体实数.一般地，如图3所示，当α为任意角时，点结合老师给出的问题，积极主动的思考，得出初步结论.激发学生好奇心，增强学习热情，更主动参与到课堂学习过程中.图2(,)P x y 的α终边上异于原点的任意一点，点P 到原点的距离为22r x y =+.我们仍然将α的正弦、余弦、正切分别定义如下.sin y r α=，cos x r α=，tan (0)yx xα=≠ 注意：当的α终边不在y 轴上时，tan α才有意义.对于每一个确定的α，其正弦、余弦及正切都分别对应一个确定的比 值，因此，正弦、余弦及正切都是以α为自变量的函数，分别叫作正弦函 数、余弦函数及正切函数.我们将正弦函数、余弦函数和正切函数统称为三角函数，通常记为： 正弦函数 y=sin x ，x R ∈； 余弦函数 cos y x =，x R ∈； 正切函数 y=tan x ，()2x k k Z ππ≠+∈.二、例题讲解例 1.如图3所示，已知角α的终边经过点(3,4)P -， 求 sin α，cos α，tan α的值.理解记忆相关概念和结论在理解的基础上熟练写出相关函数表达式和定义域直观展示知识点，让学生在理解的基础上记忆概念图2解 由已知有，x =3,y =-4,则，()234 5.r =+-=２于是4 ,5ysin r α==-3,5x cos r α==43y tan x α==-.三、巩固练习已知角α的终边分别经过以下各点，求sin cos tan .ααα，和.（1）P(-8，6)； （2）P(5，12)； （3）P （-1，2）.认真读题，积极思考，掌握解题的基本思路认真思考、完成相关题目展示问题解决的基本步骤，培养学生分析解决问题能力加深对定义和公式的理解和记忆图3一般地，α为任意角，(,)P x y 为α终边上异于原点的任意一点，点P 与原点O 的距离OP r =，因为0r >，由定义可知，正弦值的符号与点P 的纵坐标y 的符号相同； 余弦值的符号与点P 的横坐标x 的符号相同； 正切值的符号与点P 的纵坐标与横坐标的比值yx的符号相同. 请同学们将点P 的坐标与各象限角正弦值、余弦值和正切值的正负号列表.为了便于记忆，我们将 ， ， 的正负号标在各象限内，如图4所示.二、例题分析例1确定下列各值的符号.（1）() 210sin -︒； （2）17 12cos π; （3） 760tan ︒. 解 （1）因为-210°是第二象限角，所以() 2100sin -︒>. （2）由1751212πππ=+， 可看出π＜π+5π12＜π+6π12=3π2是第三象限的角， 所以 17012cos π<. （3）因为760402360︒=︒+⨯︒，可知760°的角与400的角终边相同，是第一象限的角，理解并熟记各象限角正弦值、余弦值和正切值的正负号认真读题，积极思考，了解知识运用的一般过程在理解的基础上记忆概念展示问题解决的基本方法，培养学生分析解决问题能力图4第3课时教学过程教学活动学生活动设计思路提出问题如图5所示，两个三角板上有几个特殊的锐角：30°，45°，60°.初中已研究了它们对应的正弦值、余弦值和正切值.现将角的范围进行了推广，已经在平面直角坐标系中研究了各象限角的正弦值、余弦值和正切值的符号分布规律.对于在平面直角坐标系中不属于任何象限的特殊角，如0°，90°，180°，270°等，它们的正弦值、余弦值和正切值又是多少？以180°为例，试求出它的正弦值、余弦值和正切值. 结合老师给出的问题，积极主动的思考，得出初步结论.激发学生好奇心，增强学习热情，更主动参与到课堂学习过程中.图5图6分析 在平面直角坐标系中，180°角的终边正好与x 轴的负半轴重合，如图6所示.以坐标原点为圆心、半径为单位长度的圆(简称单位圆)与x 轴交于点(1,0)P -，于是有1x =-，0y =，1γ=.根据任意角的正弦、余弦和正切的定义可知，sin 1800yr ︒==； cos 1801xr ︒==-；tan 1800yx︒==.一、探究新知一般地，取单位圆与坐标轴的交点就可以得到0°，90°，180°和270°等特殊角的正弦值、余弦值和正切值，如下表所示表中360°角与0°角的终边相同，对应的三角函数值也相同.二、例题讲解例1 求︒-︒+︒-︒270sin 7180tan 290sin 4180sin 5的值.解 ︒-︒+︒-︒270sin 7180tan 290sin 4180sin 5=5×0－4×1＋2×0－7×（－1）=3。

任意角的正弦函数、余弦函数和正切函数的定义授课时间第周星期第节课型新授课主备课人学习目标1.掌握任意角三角函数的定义，并能借助单位圆理解任意角三角函数的定义；2.会用三角函数线表示任意角三角函数的值；3.掌握正弦、余弦、正切函数的定义域和这三种函数的值在各象限的符号重点难点求任意角三角函数的值学习过程与方法自主学习1．设点P是α角终边上任意一点，坐标为(,)P x y，22||OP x y r=+=，用（1）比值叫做α的正弦，记作sinα，即sinα= ；（2）比值叫做α的余弦，记作cosα，即cosα= ；（3）比值叫做α的正切，记作tanα，即tanα= .其中，siny x=和cosy x=的定义域分别是_____________；而tany x=的定义域是_________.除上述情况外，对于确定的值α，比值yr、xr、yx分别是一个确定的实数，所以正弦、余弦、正切、是以角α为自变量，一比值为函数值的函数，分别叫做角α的正弦函数、余弦函数、正切函数，以上三种函数统称为____________．2．三角函数的符号由三角函数的定义，以及各象限内点的坐标的符号，我们可以得知：①正弦值yr对于第一、二象限为_______对于第三、四象限_______；②余弦值xr对于第一、四象限为_______对于第二、三象限为_______；③正切值yx对于第一、三象限为_______对于第二、四象限为________．说明：（1）若终边落在轴线上，则可用定义求出三角函数值；（2）正弦函数值的符号与y的符号相同，余弦函数值的符号与x的符号相同．精讲互动一、任意角的三角函数例1．已知角α的终边经过点(2,3)P-，求α的正弦、余弦、正切值.分析：任意角的三角函数的定义思考 ：若角θ的终边经过点(4,3)(0)P a a a -≠，求sin cos θθ和的值二、三角函数的定义域例2. x 取什么值时，sin cos tan x x x-有意义.（ 分 析：三角函数的定义域）三、三角函数值在各象限的符号例3 确定下列三角函数的符号：（1）7cos12π； （2）0sin(465)-； （3）11tan 3π达标训练1设α是三角形一个内角，在sin ,cos ,tan ,tan2αααα中，哪些有可能是负值？ 2确定下列各角的正弦、余弦、正切值的符号：（1）0885； （2）0395-； （3）196π； （4）253π- 3 已知角α的终边经过点(3,4)P -，求角α的正弦、余弦和正切值.作业布置习题1-4 1，2，6 学习小结/教学反思。

任意角的三角函数及基本公式三角函数是数学中的一个重要概念，它们描述了角度与三角比之间的关系。

任意角的三角函数包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。

下面将详细介绍这些函数的定义、基本公式以及它们之间的关系。

1. 正弦函数（sine function）：在单位圆上，从x轴正向到射线与单位圆的交点之间的弧度即为角的弧度。

正弦函数将给定角度的正弦值映射到数轴上。

其定义如下：sin(θ) = y/r其中θ为角度，y为对边，r为斜边。

2. 余弦函数（cosine function）：余弦函数表示角的余弦值在数轴上的投影长度。

其定义如下：cos(θ) = x/r其中θ为角度，x为邻边，r为斜边。

3. 正切函数（tangent function）：正切函数表示角的正切值在数轴上的投影比。

其定义如下：tan(θ) = y/x其中θ为角度，y为对边，x为邻边。

4. 余切函数（cotangent function）：余切函数表示角的余切值在数轴上的投影比。

其定义如下：cot(θ) = x/y其中θ为角度，y为对边，x为邻边。

5. 正割函数（secant function）：正割函数表示角的正割值在数轴上的投影长度。

其定义如下：sec(θ) = r/x其中θ为角度，x为邻边，r为斜边。

6. 余割函数（cosecant function）：余割函数表示角的余割值在数轴上的投影长度。

其定义如下：csc(θ) = r/y其中θ为角度，y为对边，r为斜边。

这些函数在不同的角度上有不同的值，可以通过查表或计算器得到具体数值。

同时，它们之间存在一些基本公式和关系，如下：1. 互余关系（co-function identities）：sin(θ) = cos(90° - θ)cos(θ) = sin(90° - θ)tan(θ) = cot(90° - θ)cot(θ) = tan(90° - θ)sec(θ) = csc(90° - θ)csc(θ) = sec(90° - θ)2.三角函数的平方和差：sin²(θ) + cos²(θ) = 1tan²(θ) + 1 = sec²(θ)cot²(θ) + 1 = csc²(θ)3.三角函数的倒数：sec(θ) = 1/cos(θ)csc(θ) = 1/sin(θ)cot(θ) = 1/tan(θ)4.符号关系：根据角度的位置和象限，三角函数的值可能为正或负。

5.3任意角的正弦函数、余弦函数和正切函数【教学目标】1、掌握任意角的三角函数的定义.2、理解终边相同的角的三角函数值相等.【教学重点】任意角的三角函数的定义.【教学难点】任意角的三角函数的定义及其运算.【教学过程】(一) 复习提问1.角的概念。

2.终边相同的角。

（︒⋅+=360k αβ)(Z k ∈）3.锐角三角函数的定义： AB BC A ==斜边对边sin ， AB AC A ==斜边邻边cos ，AC BC A ==邻边对边tan . （二）讲授新课1.任意角的三角函数的定义问题（1）：如何将上述的三角形放入直角坐标系中？学生回答：将A ∠的顶点即点A 与坐标原点重合，将其始边AC 与坐标系中 轴的非负半轴重合.问题（2）：原有的线段AC 、BC 、AB 将如何改写？要求并引导学生将这三个距离用坐标x 和y 表示.此时可根据学生的情况采用分小组讨论的方法进行。

学生根据现有的图形，将刚才的定义进行改写：x AC =，y BC =，r y x AB =+=22(勾股定理)。

把这三个式子带入原始的定义中去可以得到：sin y r α= , cos x r α= , tan y x α=给学生两分钟时间记忆公式并由教师提问以加深记忆效果。

问题（3）：若角的终边落在其他象限，如何求呢？当角的终边在第二、第三、第四象限的时候，其三个三角函数值的计算公式与上述的完全相同，但符号发生了变化：第一象限：0>x ，0>y ，0>r ；第二象限：0<x ，0>y ，0>r ；第三象限：0<x ，0<y ，0>r ；第四象限：0>x ，0<y ，0>r 。

可以看出：x 与y 是随着象限的变化而不同，但r 永远为正。

例1 已知角α的终边经过点)3,2(-P ，求α的三个三角函数值.解：∵3,2=-=y x ，∴133)2(2222=+-=+=y x r . ∴ 13133133s i n ===r y α，13132132cos -=-==r x α，2323tan -====x y α。