四川大学理论力学第十三章
- 格式:ppt
- 大小:747.00 KB
- 文档页数:46


aIN第十三章 达朗贝尔原理[习题13-1] 一卡车运载质量为1000kg 的货物以速度h km v /54=行驶。
设刹车时货车作匀减速运动,货物与板间的摩擦因数3.0=s f 。
试求使货物既不倾拿倒又不滑动的刹车时间。
解:以货物为研究对象,其受力如图所示。
图中, 虚加惯性力之后,重物在形式上“平衡”。
货物不滑动的条件是:即货物不滑动的条件是:)(1.5s t ≥…………(1) 货物不倾倒(不向前倾倒)的条件是:)(06.38.93030s g t ==≥…………(2) (1)(2)的通解是)(1.5s t ≥。
即,使货物既不倾拿倒又不滑动的刹车时间是)(1.5s t ≥。
[习题13-2] 放在光滑斜面上的物体A ,质量kg m A 40=,置于A 上的物体B ,质量kg m B 15=;力kN F 500=,其作用线平行于斜面。
为使A 、B 两物体不发生相对滑动,试求它们之间的静摩擦因素s f 的最小值。
解:以A 、B 构成的质点和系为研究对象,其受力如图所示。
在质心加上惯性力后,在形式上构成平面一般“平衡”力系。
以B 为研究对象,其受力如图所示。
由达朗伯原理得:305.05.0191.48.9866.0191.430sin 30cos 00=⨯+⨯=+≥a g a f s ,即: [习题13-3] 匀质杆AB 的质量kg m 4=,置于光滑的水平面上。
在杆的B 端作用一水平推力N F 60=,使杆AB 沿F 力方向作直线平动。
试求AB 杆的加速度a 和角θ的值。
解:以AB 杆为研究对象,其受力与运动分析如图所示。
由达朗伯原理得:[习题13-4] 重为1P 的重物A ,沿光滑斜面D 下降,同时借一绕过滑轮C 的绳子而使重为2P 的重物B 运动,斜面与水平成θ角。
试求斜面D 给凸出部分E 的水平压力。
解:以A 为研究对象,其受力与运动分析如图所示。
由达朗伯原理得:EN D0sin 11=--a gP T P B θ………(1) 以B 为研究对象,其受力与运动分析如图所示。

第十三章达朗贝尔原理(动静法)达朗贝尔原理:用静力学中研究平衡问题的方法来研究动力学问题,因此又称为动静法。
第四篇分析力学基础包含第十三章达朗贝尔原理(动静法)和第十四章虚位移原理()e C i ma F ⎧=∑⎪⎨⎪⎩ ()()e C CJ M F α=∑ 应用质心运动定理和相对于质心的动量矩定理------刚体平面运动微分方程:()()()()00e i Ii e c i c Ii F M F M F ⎧-=⎪⎨-=⎪⎩∑∑∑∑ 这是外力系的主矢这是外力系的主矩()()()00e i Ce cc iF ma dL M F dt ⎧∑-=⎪⎨-=⎪⎩∑ IR C F ma ⎧=-⎪⎨⎪⎩Ic c M J α=-称为惯性力系的主矢称为惯性力系的主矩()()()00e i IR e c i Ic F F M F M ⎧-=⎪⎨-=⎪∑∑这就是达朗贝尔原理N§13-1 惯性力·质点的达朗贝尔原理N ma F F =+N F F ma +-=I F ma =-→令称为惯性力。
N I F F F ++= 有:质点的达朗贝尔原理:作用在质点上的主动力、约束力和虚加的惯性力在形式上组成平衡汇交力系。
由牛顿第二定律,有F a =--∑ 为合力,方向与相同这是合成方程形式这是平衡方程形式mamFN F I F非平衡的刚体,产生加速度,产生惯性力。
将惯性力看作外力,加到非平衡力系中,使非平衡力系变成平衡力系.例13-1:已知:60,m 3.0,kg 1.0===θl m 求:, .Tv Fθsin 2l vmma F n n I==0T I mg F F ++= 0,0,b n F F ⎧=⎪⎨=⎪⎩∑∑解得:N96.1cos ==θmgF T s m1.2sin 2==ml F v T θ解:小球作均匀速圆周运动,只有法向惯性力:重力、绳拉力、惯性力形式上组成平衡力系。
列平衡方程:1cos 0sin 0nT I F mg F F θθ-=⎧⎨-=⎩TF IF 就是离心力。




习 题13-1 如图13-16所示,一飞机以匀加速度a 沿与水平线成仰角b 的方向作直线运动。
已知装在飞机上的单摆的悬线与铅垂线所成的偏角为f ,摆锤的质量为m 。
试求此时飞机的加速度a 和悬线中的张力F T 。
图13-16ma F =I 0cos sin 0I T =-=∑βϕF F F xϕβsin cos IT F F =0sin cos 0I T =--=∑mg F F F y βϕ0sin cos sin cos I I =--mg F F βϕϕβ0sin )cos(I=-+mg F ϕβϕ mgma=+ϕβϕsin )cos()cos(sin βϕϕ+=g amg maF F )cos(cos sin cos sin cos I T βϕβϕβϕβ+===13-2 球磨机的简图如图13-17所示,滚筒作匀速转动,内装钢球及被粉碎的原料,当钢球随滚筒转到某一角度f 时,将脱离筒壁作抛射运动,由于钢球的撞击,从而破碎与研磨原料。
已知钢球脱离筒壁的最佳位置'4054︒=ϕ,滚筒半径R =0.6m 。
试求使钢球在'4054︒=ϕ处脱离滚筒的滚筒转速。
图13-172n I ωmR ma F == 0cos 0I N n =-+=∑F mg F F ϕ)cos (cos cos 22I N ϕωϕωϕg R m mg mR mg F F -=-=-=令0N =F0cos 2=-ϕωg RR g ϕωcos =min r/35.296.00454cos 8.9π30cos π30π30='︒⨯===R g n ϕω13-3 一质量为m 的物块A 放在匀速转动的水平转台上,如图13-18所示。
已知物块的重心距转轴的距离为r ,物块与台面之间的静摩擦因数为s μ。
试求物块不致因转台旋转而滑出时水平转台的最大转速。
图13-182n I ωmr ma F == 00N =-=∑mg F F ymg F =N00I =-=∑F F F x0N s 2=-F mr μω 0s 2=-mg mr μωrgs μω=rgn s max π30π30μω==13-4 离心调速器的主轴以匀角速度w 转动,如图13-19所示。


理论力学试题库题型:A填空题,B选择题,C简答题,D判断题,E计算题,F综合题,G作图题。
编号E04001中,E表示计算题,04表示内容的章节号即题目内容属于第04章,001表示章节题号的序号,即此题是第04章计算题的001号题。
计算题:13:E13001. (10分)如图E13001所示长方形均质平板,质量为27kg,由两个销A 和B悬挂。
如果突然撤去销B,求在突然去销B的瞬时平板的角速度和销A的约束力。
图E13001E13002. (10分)如图E13002所示,由相互铰接的水平臂连成的传送带将圆柱零件从一个高度传送至另一个高度。
设零件与臂之间的摩擦系数fs=0.2。
求(1)降落加速度a多大时零件不致于在水平臂滑动;(2)在此加速度a下,比值h/d 等于多少时零件在滑动之前先倾倒。
图E13002E13003.(10分)图示由相互铰接的水平臂连成的传送带,将圆柱形零件从一高度传送到另一个高度。
设零件与臂之间的摩擦因数fs=0.2。
求:(1)降落加速度a为多大时,零件不致在水平臂上滑动;(2)在此加速度a下,比值h/d等于多少时,零件在滑动之前先倾倒。
图E13003E13004.(10分)图示汽车总质量为m,以加速度a作水平直线运动。
汽车质心G离地面的高度为h,汽车的前后轴到通过质心垂线的距离分别等于c和b。
求其前后轮的正压力;又,汽车应如何行驶能使前后轮的压力相等?图E13004E13005.(10分)图示均质矩形块质量,置于平台车上,车质量,此车沿光滑的水平面运动,不计定滑轮质量。
车和矩形块在一起由质量为的物体牵引,使之作加速运动。
设物块与车之间的摩擦力足够阻止相互滑动,求能够使车加速运动的质量的最大值,以及此时车的加速度大小。
图E13005E13006.(10分)调速器由两个质量为的均质圆盘构成,圆盘偏心地铰接于距转轴为a 的A,B两点。
调速器以等角速度绕铅垂轴转动,圆盘中心到悬挂点的距离为l。
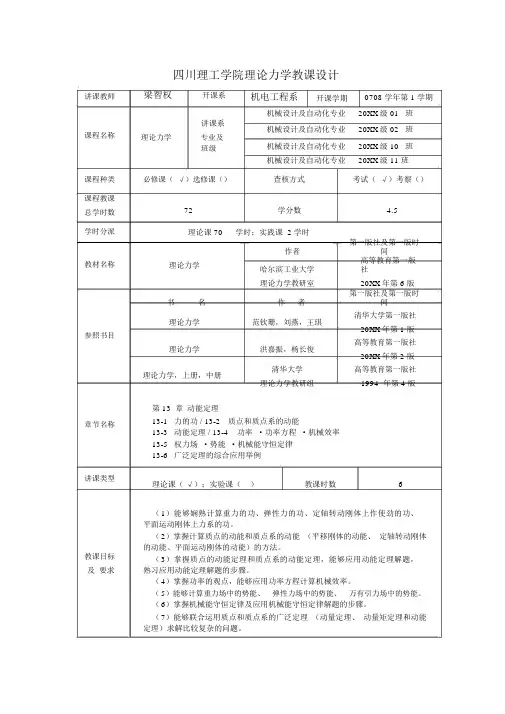
四川理工学院理论力学教课设计讲课教师课程名称课程种类课程教课梁智权开课系讲课系理论力学专业及班级必修课(√)选修课()机电工程系开课学期0708 学年第 1 学期机械设计及自动化专业20XX 级 01班机械设计及自动化专业20XX 级 02班机械设计及自动化专业20XX 级 10班机械设计及自动化专业20XX 级 11 班查核方式考试(√)考察()总学时数学时分派教材名称参照书目章节名称讲课类型教课目标及要求72学分数 4.5理论课 70学时;实践课 2 学时作者第一版社及第一版时间理论力学哈尔滨工业大学高等教育第一版社理论力学教研室20XX 年第 6 版书名作者第一版社及第一版时间理论力学范钦珊,刘燕,王琪清华大学第一版社20XX 年第 1 版理论力学洪嘉振,杨长俊高等教育第一版社20XX 年第 2 版理论力学,上册,中册清华大学高等教育第一版社理论力学教研组1994 年第 4 版第 13章动能定理13-1力的功 / 13-2质点和质点系的动能13-3动能定理 / 13-4功率·功率方程·机械效率13-5权力场·势能·机械能守恒定律13-6广泛定理的综合应用举例理论课(√);实验课()教课时数6(1)能够娴熟计算重力的功、弹性力的功、定轴转动刚体上作使劲的功、平面运动刚体上力系的功。
(2)掌握计算质点的动能和质点系的动能(平移刚体的动能、定轴转动刚体的动能、平面运动刚体的动能)的方法。
(3)掌握质点的动能定理和质点系的动能定理,能够应用动能定理解题,熟习应用动能定理解题的步骤。
(4)掌握功率的观点,能够应用功率方程计算机械效率。
(5)能够计算重力场中的势能、弹性力场中的势能、万有引力场中的势能。
(6)掌握机械能守恒定律及应用机械能守恒定律解题的步骤。
(7)能够联合运用质点和质点系的广泛定理(动量定理、动量矩定理和动能定理)求解比较复杂的问题。
教课内容概要能量变换与功之间的关系是自然界中各样形式运动的广泛规律,在机械运动中则表现为动能定理。
