四川大学理论力学第十二章
- 格式:ppt
- 大小:1.09 MB
- 文档页数:24


第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
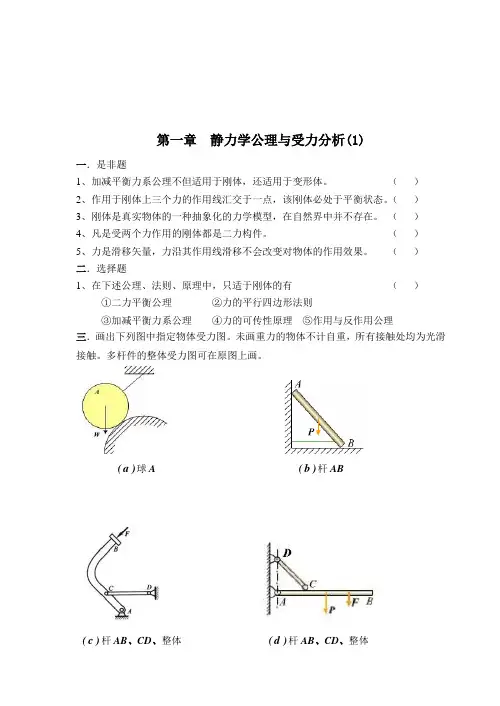
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A )b(杆ABd(杆AB、CD、整体)c(杆AB、CD、整体)-2 -)e (杆AC 、CB 、整体)f (杆AC 、CD 、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a (球A 、球B 、整体)b (杆BC 、杆AC 、整体班级姓名学号- 3 -第一章静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WA DBCEOriginal FigureADBCEWWF AxF Ay F BFBD of the entire frame )a(杆AB、BC、整体)b(杆AB、BC、轮E、整体)c(杆AB、CD、整体)d(杆BC带铰、杆AC、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体- 4 -班级姓名学号- 5 -第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。

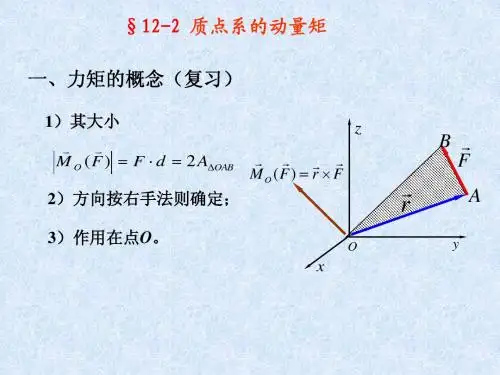
动量矩定理12-1 质量为m 的点在平面Oxy 内运动,其运动方程为: x a cos t y bsin2 t 式中a 、b 和 为常量。
求质点对原点 O 的动量矩。
解:由运动方程对时间的一阶导数得原点的速度V xdxsin t dt aV y dy 2b cos2 t 质点对点 O 的动量矩为L O M o (mV x ) M 0(mV y )mv x y mv y x m ( a sin t) bsin2 t m 2b cos2 t acos t 2mab cos 3 t 12-3 如图所示,质量为m 的偏心轮在水平面上作平面运动。
轮子轴心为A,质心为C, AC = e ;轮子半径为 R,对轴心A 的转动惯量为J A ; C 、A 、B 三点在同一铅直线上。
(1 )当轮子只 滚不滑时,若 V A 已知,求轮子的动量和对地面上 B 点的动量矩。
(2)当轮子又滚又滑时, 若V A 、 已知,求轮子的动量和对地面上 B 点的动量矩。
解:(1)当轮子只滚不滑时 B 点为速度瞬心。
轮子角速度V A R质心C 的速度V CBCR e轮子的动量p mv Cmv A (方向水平向右)R对B 点动量矩L B J B2 2 2由于 J B J C m (R e) J A me m (R e) 故 L B J A me 2 m (R e )2食 (2)当轮子又滚又滑时由基点法求得 C 点速度。
V C V A V CA V A e 轮子动量 p mv C m(v A e) (方向向右) 对B 点动量矩L B mv C BC J Cm(v A 2e) (R e) (J A me) mv A (R e) (J A mRe) 12-13 如图所示,有一轮子,轴的直径为 50 mm 无初速地沿倾角 20的轨道滚下,设 只滚不滑,5秒内轮心滚动的距离为 s =3m 。
试求轮子对轮心的惯性半径。
解:取轮子为研究对象,轮子受力如图( a )所示,根据刚体平面运动微分方程有 ma C mgsi n F ( 1) J C = Fr ( 2)因轮子只滚不滑,所以有 a c = r ( 3) ® 12将式(3)代入式(1)、(2)消去F 得到mr sinm?g上式对时间两次积分,并注意到 t = 0时 0, 0,则 mgrt 2 sin mgrt 2s in 2(J C mr 2) 2(m 2 mr 2) 把 r = 0.025 m 及 t = 5 s 时,s 'grt 2sin f gt 2sin-r r「s r 1grt 2sin 2( 2 r 2) r 3 m 代入上式得0.0259.8 52si n202 30.09 m 90 mm12-17 图示均质杆 AB 长为I ,放在铅直平面内,杆的一端 A 靠在光滑铅直墙上,另一端 B 放在光滑的水平地板上,并与水平面成 °角。


理论力学Ⅰ第 8 版课后习题答案目录:
第一章静力学公理和物体的受力分析
第二章平面力系
第三章空间力系
第四章摩擦
第五章点的运动学
第六章刚体的简单运动
第七章点的合成运动第
八章刚体的平面运动
第九章质点动力学的基本方程
第十章动量定理
第十一章动量矩定理
第十二章动能定理
第十三章达朗贝尔定理
第十四章虚位移定理
第一章
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
第二章
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕。



第一章静力学基础理论力学绪论§1-1 力和刚体§1-2 静力学公理§1-3 约束、约束类型§1-4 主动力,主动力分类§1-5 物体的受力分析,受力图§1-6 静力学计算机计算代码规定物体受力例题第二章力系的简化与合成§2-1 力对点的矩和力对轴的矩§2-2 基本力系----汇交力系和力偶系§2-3 力线平移定理§2-4 空间力系向一点简化,主矢和主矩§2-5 空间力系向一点简化结果分析第三章任意力系的平衡第四章静力学专题讨论第五章力系平衡条件下的计算机计算原理第六章点的运动学运动学引言§6-1 矢量法§6-2 直角坐标法§6-3 自然法§6-4 实例第七章刚体的简单运动§7-1 刚体的平行移动§7-2 刚体绕定轴的转动§7-3 转动刚体内各点的速度和加速度§7-4 轮系的传动比§7-5 矢量表示角速度和角加速度刚体简单运动例题第八章点的合成运动§8-1 相对运动.牵连运动.绝对运动§8-2 点的速度合成定理点的速度合成分析计算步骤:1. 选动点, 动坐标系2. 分析三种运动(绝对运动,相对运动,牵连运动),速度分析。
3. 速度合成定理: 建立动点速度的关系4. 计算速度§8-3 牵连动运动是平动时点的加速度合成定理加速度求解步骤1. 取动点,动系2.分析三种运动3. 速度分析4.加速度分析§8-4 牵连运动是转动时点的加速度合成定理. 科氏加速度第九章刚体的平面运动§9-1 刚体平面运动的概述和运动分解§9-2 求平面图形内各点速度的基点法§9-3 求平面图形内各点速度的瞬心法§9-4 用基点法求平面图形内各点的加速度§9-5 运动学综合应用举例§9-6 刚体绕平行轴转动的合成第十章运动构件系统分析和计算机计算§10-1 刚体一般运动概述§10-2 构件系统运动分析§10-3 构件系统运动计算机计算第十一章质点动力学基本方程§11-1 动力学的基本定律§11-2 质点的运动微分方程§11-3 质点动力学的两类基本问题质点动力学第一类基本问题例题质点动力学第二类基本问题例题§11-4 质点相对运动动力学的基本方程质点相对运动动力学问题例题第十二章动量定理§12-1 动量与冲量§12-2 动量定理§12-3 质心运动定理第十三章动量矩定量§13– 1 质点和质点系的动量矩§13– 2 动量矩定理§13– 3 刚体绕定轴的转动微分方程§13–4 刚体对轴的转动惯量§13–5 质点系相对于质心的动量矩定理§13-6 刚体的平面运动微分方程第十四章动能定理§14-1 力的功§14-2 质点和质点系的动能§14-3 动能定理§14-4 功率.功率方程.机械效率§14-5 势力场.势能.机械能守恒定律§14-6 普遍定理的综合应用举例第十五章碰撞(动力学专题)§15-1 碰撞现象碰撞力§15-2 普遍定理在碰撞过程的应用§15-3 恢复系数§15-4 碰撞问题举例§15-5 碰撞冲量对绕定轴转动刚体的作用撞击中心第十六章达朗贝尔原理§16-1 惯性力.质点的达朗贝尔原理§16-2 质点系的达朗贝尔原理§16-3 刚体惯性力系的简化§16-4 绕定轴转动刚体的轴承动反力第十七章虚位移原理§17-1 约束虚位移虚功§17-2 虚位移原理§17-3 自由度和广义坐标§17-4 以广义坐标表示的质点系平衡条件第十八章分析力学基础§18-1 自由度和广义坐标§18-2 以广义坐标表示的质点系平衡条件§18-3 动力学普遍方程§18-4拉格朗日方程第十九章机械振动基础§19-1 单自由度系统的自由振动§19-2 计算固有频率的能量法§19-3 单自由度系统的有阻尼自由振动§19-4 单自由度系统的无阻尼受迫振动§19-5 单自由度系统的有阻尼受迫振动§19-6 转子的临界转速§19-7 隔振。

理论力学(盛冬发)课后习题答案ch12|第12章动能定理.143.第12章动能定理1,真或假问题(括号内正确打勾,错误打勾“*”)1。
当一个圆形车轮纯滚动时,与地面接触点的法向约束力和滑动摩擦力不起作用。
(√) 2。
理想约束的约束反力所做的功之和等于零(√) 3。
因为粒子系统中的内力成对出现,所以内力功的代数和等于零(×) 4。
弹簧压缩了10厘米,从原来的长度延长了10厘米,弹簧力也同样起作用。
(√) 5。
粒子系统动能的变化与作用在粒子系统上的外力有关,而与内力无关。
(×) 6。
如果相同质量的三个粒子以相同的初始速度从相同的高度向上、水平和向下抛向地面,这三个粒子将以相同的速度落到地面。
(√)7。
动能定理的方程是向量(×) 8。
弹簧从其自然位置拉长10厘米,再拉长10厘米。
在这两个过程中,弹力的作用是相等的。
(x) 2。
填写问题1。
当一个粒子刚刚在一个垂直平面上转动一次,它的重力做功是02.在理想约束条件下,约束反力所做功的代数和为零3。
如图12.19所示,质量为m1的均质杆OA的一端铰接在质量为m2的均质圆形车轮的车轮中心,另一端位于水平面上。
圆形的轮子在地上滚动。
如果车轮中心的速度是vo,系统的动能t?1322m1v0?M2v0244..圆轮的一端连接一个刚度系数为K的弹簧,另一端连接一个重量为P的重物,如图12.201所示最初,春天自然很长。
当重量降到h时,系统的总功w?博士?kh22 o VO a k p h图12.19图12.205。
如图12.21所示,滑块a和滑块BC之间的摩擦力是系统的内力。
假设已知的摩擦力是f,等于一个常数,曲柄每转一周的摩擦力功是?4Fr6。
平行四边形机构如图12.22,O1A?O2B?R,O1A//O2B,以角速度转动O1A?5次旋转如果所有的棒都是同质的,质量是m,那么动能T =mr2?26. 143 .. 144 .理论力学7。