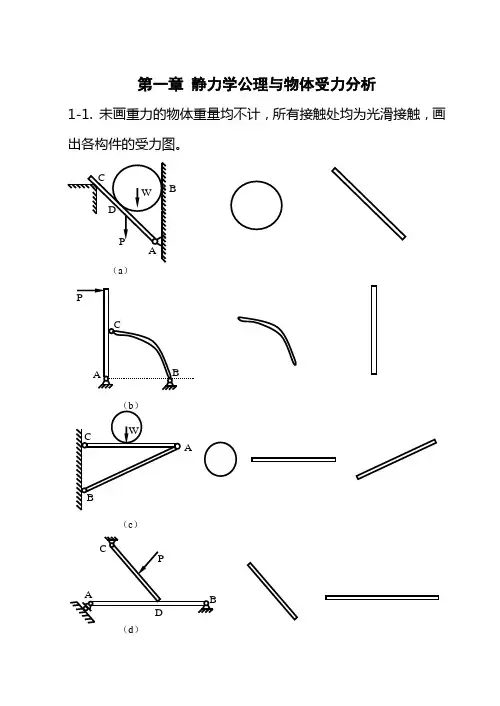
理论力学第11章习题答案

第十一章 轮系一、学习指导与提示工程中实际应用的齿轮机构经常以齿轮系(简称轮系)的形式出现，它用来获得大传动比、变速和换向、合成或分解运动以及距离较远的传动。

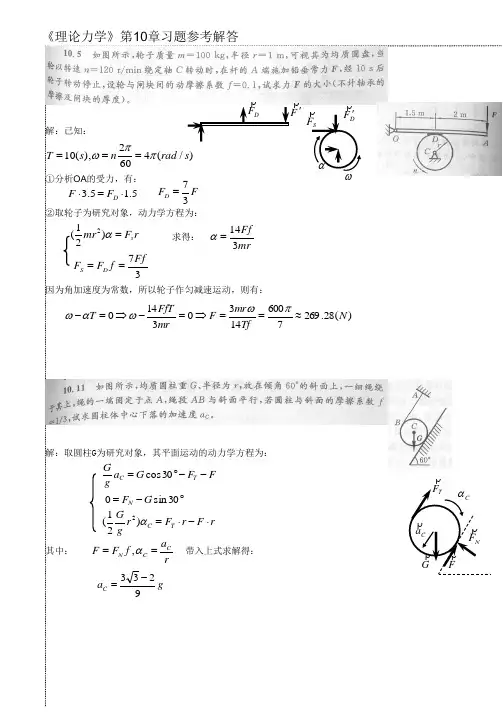
轮系可分为定轴轮系和周转轮系两大类，所谓复合轮系只不过是既包含定轴轮系又包含周转轮系，或几部分周转轮系组成的复杂轮系。

因此，首要的是弄清定轴轮系和周转轮系的本质属性，并掌握它们各自的传动比计算方法，在此基础上，只要注意正确区分轮系，就可以将一个复杂的复合轮系分解为若干个单一周转轮系和定轴轮系，这是学习轮系传动比计算的一个总体原则，应当牢牢把握。

本章的主要内容是：（1）轮系的应用和分类；（2）定轴轮系及其传动比；（3）周转轮系及其传动比；（4）复合轮系及其传动比；（5）特殊行星传动简介。

1．定轴轮系一个轮系，若运动过程中，所有齿轮的几何轴线的位置都是固定不变的，则可判定该轮系为定轴轮系(亦称普通轮系)。

注意：这里指的是几何轴线位置固定，并不是该轴不能转动，无论该轴是转动的，或不转动的（与机架相联），只要几何轴线位置不变，就是定轴的。

定轴轮系传动比计算公式：()各主动轮齿数连乘积各从动轮齿数连乘积J G J G n n i mJ G GJ →→-==1 （11.1） 上述公式包含两方面的问题：传动比GJ i 的大小，以及主从动转速 n G 、n J 之间的转向关系（即传动比的正负号），m 为外啮合齿轮对数。

但需注意：① 只有在J G →传动路线中无空间齿轮，各轮几何轴线均互相平行的情况下，公式中()m 1-才有其特定意义，可以用其来表示n G 、n J 之间的转向关系。

若计算结果GJ i 为正，说明G 、J 两轮转向相同；若为负，则说明G 、J 两轮转向相反。

② J G →传动路线中有空间齿轮（如锥齿轮、蜗轮蜗杆），如图11.1所示，各轮转向只能用标注箭头法确定，()m 1-没有意义。

图11.12．周转轮系轮系中至少有一齿轮的几何轴线不固定，而是绕另一轴线位置固定的齿轮回转，这样的轮系，就是周转轮系。

习 题11-1 质量为m 的质点在平面Oxy 内运动，其运动方程为：t b y t a x ωω2sin ,cos ==。

其中a 、b 和w 均为常量。

试求质点对坐标原点O 的动量矩。

t a xv x ωωsin -== t b y v y ωω2cos 2== x mv y mv L y x O +-=)cos 2cos 22sin sin (t a t b t b t a m ωωωωωω⨯+⨯= )cos 2cos 22sin (sin t t t t mab ωωωωω⨯+⨯= )cos 2cos 2cos sin 2(sin t t t t t mab ωωωωωω⨯+⨯= )2cos (sin cos 22t t t mab ωωωω+= t mab ωω3cos 2=11-2 C 、D 两球质量均为m ，用长为2 l 的杆连接，并将其中点固定在轴AB 上，杆CD 与轴AB 的交角为θ，如图11-25所示。

如轴AB 以角速度w 转动，试求下列两种情况下，系统对AB 轴的动量矩。

（1）杆重忽略不计；（2）杆为均质杆，质量为2m 。

图11-25(1)θθ222sin 2)sin (2ml l m J z =⨯= θω22sin 2l m L z = (2)θθ2202sin 32d )sin (2ml x x lm J l z ==⎰杆 θ22sin 38ml J z = θω22sin 38l m L z =11-3 试求图11-26所示各均质物体对其转轴的动量矩。

各物体质量均为m 。

图11-26(a) ω231ml L O =(b) 22291)6(121ml l m ml J O =+= ω291ml L O -=(c) 2222452312121ml l m l m J O =⨯⨯+⨯⨯=ω2245ml L O = (d) 2222321mR mR mR J O =+= ω223mR L O =11-4 如图11-27所示，均质三角形薄板的质量为m ，高为h ，试求对底边的转动惯量J x 。

第11章 动量矩定理一、是非题(正确的在括号内打“√”、错误的打“×”)1. 质点系对某固定点(或固定轴)的动量矩，等于质点系的动量对该点(或轴)的矩。

(×)2. 质点系所受外力对某点(或轴)之矩恒为零，则质点系对该点(或轴)的动量矩不变。

(√)3. 质点系动量矩的变化与外力有关，与内力无关。

(√)4. 质点系对某点动量矩守恒，则对过该点的任意轴也守恒。

(√)5. 定轴转动刚体对转轴的动量矩，等于刚体对该轴的转动惯量与角加速度之积。

(×)6. 在对所有平行于质心轴的转动惯量中，以对质心轴的转动惯量为最大。

(×)7. 质点系对某点的动量矩定理e 1d ()d nOO i i t ==∑L M F 中的点“O ”是固定点或质点系的质心。

(√)8. 如图所示，固结在转盘上的均质杆AB ，对转轴的转动惯量为20A J J mr =+ 2213ml mr =+，式中m 为AB 杆的质量。

(×)9. 当选质点系速度瞬心P 为矩心时，动量矩定理一定有e 1d()d nP P i i t ==∑L M F 的形式，而不需附加任何条件。

(×)10. 平面运动刚体所受外力对质心的主矩等于零，则刚体只能做平动；若所受外力的主矢等于零，刚体只能作绕质心的转动。

(×)图二、填空题1. 绕定轴转动刚体对转轴的动量矩等于刚体对转轴的转动惯量与角速度的乘积。

2. 质量为m ，绕z 轴转动的回旋半径为ρ，则刚体对z 轴的转动惯量为2ρm J z =。

3. 质点系的质量与质心速度的乘积称为质点系的动量。

4. 质点系的动量对某点的矩随时间的变化规律只与系统所受的外力对该点的矩有关，而与系统的内力无关。

5. 质点系对某点动量矩守恒的条件是质点系所受的全部外力对该点之矩的矢量和等于零，质点系的动量对x 轴的动量矩守恒的条件是质点系所受的全部外力对x 轴之矩的代数和等于零。

第11章动能定理即质点系的动能等于其随质心平BCθABθCPA2rOr C力的功2rOr CAP2rOr CAP2rOr CAPs汽车驱动问题能量角度：汽缸内气体爆炸力是内力，不改变汽车的动量，但使汽车的动能增加。

动量角度：地面对后轮的摩擦力是驱动力，使汽车的动量增加，但不做功，不改变汽车的动能。

内力不能改变质点系的动量和动量矩，但可以改变能量；外力能改变质点系的动量和动量矩，但不一定能改变能量。

例题11-8水平悬臂梁AB，B端铰接滑轮B，匀质滑轮质量m1，半径r；绳一端接滚，轮C，半径r，质量m2视为质量集中在边缘；绳另端接重物D，质量m3。

求重物加速度。

CωDv BωCv 解：末位置是一般位置hconst 01==T T =2T 2321D v m 221B B J ω+221CP J ω+运动学关系rr v v B C C D ωω===2121rm J B =2222222rm r m r m J P=+=2321222121Dv m m m T ⎟⎠⎞⎜⎝⎛++=gh m W 312=CωDv BωCv h1212W T T =−gh m T v m m m D 30232122121=−⎟⎠⎞⎜⎝⎛++对t 求导h g m vv m m m D D &&33210)221(=−++Dv h =&D D a v=&gm m m m a D 3213221++=例11-9匀质圆盘和滑块的质量均为m。

圆盘的半径为r。

杆平行于斜面，其质量不计。

斜面的倾斜角为θ。

圆盘、滑块与斜面的摩擦因数均为μ。

圆盘在斜面上作纯滚动。

试求滑块下滑加速度。

1212W T T =−01=T 2222212121mvJ mv T A ++=ω解()sF F mgs mgs W B A +−+=θθsin sin 12θμcos mg F F B A ==取导221,mrJ v r A ==ω2245mvT =()θμθcos sin 2452−=gs v a v v s==&&,()θμθcos sin 54−=g a F A 是静摩擦力，理想约束，不作功。

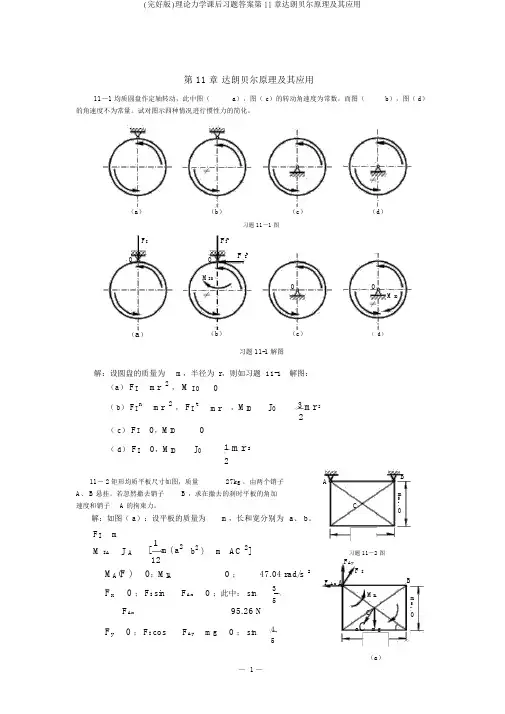
第 11 章 达朗贝尔原理及其应用11－1 均质圆盘作定轴转动，此中图（ a ），图（ c ）的转动角速度为常数，而图（ b ），图（ d ）的角速度不为常量。

试对图示四种情况进行惯性力的简化。

≠≠（a ）（b ）（c ）（d ）习题 11－1 图F I F I nOO F I tM I OO O≠M IO≠（a ）（b ）（c ）（ d ）习题 11-1 解图解：设圆盘的质量为m ，半径为 r ，则如习题 11-1 解图：（a ） F I mr 2 ， M I O 0（ b ） F I nmr 2 ， F I tmr ，M IOJ O3 mr 22（ c ） F I 0，M IO 0（ d ） F I0，M IOJ O1 mr 2211－ 2 矩形均质平板尺寸如图，质量 27kg ，由两个销子AA 、B 悬挂。

若忽然撤去销子 B ，求在撤去的刹时平板的角加速度和销子A 的拘束力。

C解：如图（ a ）：设平板的质量为 m ，长和宽分别为 a 、 b 。

F I mM I AJ A[ 1m( a 2 b 2 ) m AC 2] 习题 11－2 图122F AyM A (F ) 0；M IA 0 ； 47.04 rad/s F IF Ax AF x0 ； F I sinF Ax0 ；此中： sin3M IA 5CF Ax95.26 NF y0 ； F I cosF Aymg0 ； sin4aC mg5Bm5 1 .Bm51.F Ay 27 9.8 3.375 47.04 0.8 137.6 N11－ 3 在均质直角构件 ABC 中， AB 、 BC 两部分的质量各为 AE 保持在图示地点。

若忽然剪断绳索，求此刹时连杆 AD 、 BE已知 l = 1.0m ， φ= 30o 。

3.0kg ，用连杆 AD 、 DE 以及绳索所受的力。

连杆的质量忽视不计，C解：如图（ a ）：设 AB 、 BC 两部分的质量各为 m = 3.0kg 。

第十一章 动量矩定理
答 案
11-1
11-2
质点系对任一点的动量矩为 ，当 时，对所有点的动量矩 都相等，即 。

11-3
11-4
不对。

11-5
圆盘作平移，因为圆盘所受的力对其质心的矩等于零，且初始角速度为零。

11-6
（a）质心不动，圆盘绕质心加速转动。

（b）质心有加速度 a=F/m ，向左；圆盘平移。

（c）质心有加速度 a=F/m ，向右；圆盘绕质心加速转动。

11-7
轮心加速度相同，地面摩擦力不同。

11-8
（1）站在地面看两猴速度相同，离地面的高度也相同；
（2）站在地面看两猴速度相同，离地面的高度也相同。

11-9
A，C正确。

11-10
均不相同。

由对定点的动量矩定理判定。