说课 高斯定理

课堂教学设计4：高斯定理【授课内容】：高斯定理【所在章节】：第7章：静电场与恒定电场7.2节：高斯定理【授课对象】：2018级大数据学院（软件工程、数字工程、网络工程专业）【教学学时】：2学时一、学情分析（一）教材内容分析本书将“高斯定理”编排在第7 章“静电场”的第2节，是整个电学部分两个基本定理之一。

在本节之前，教材已经介绍了库仑定律求解真空中静止点电荷周围激发的静电场问题，学生感觉利用该定律求解静电场在有些情况下比较复杂．本节内容安排了从特殊到一般的高斯定理的归纳过程，由特殊的以点电荷为球心的球面积分模型出发，进行不断变化，最终得出一般表达式，让学生亲身经历高斯定理的推导过程．根据电荷的分布特点，选择适当的高斯面，使用此定理能够更为方便地求出具有对称性分布的电场强度，将高斯定理与库仑定律联系对比，使学生认识到用高斯定理求解具有某种对称性的带电体周围分布的电场时较一般方法更加简单方便．同时也说明了静电场是有源场．电场中高斯定理的学习为之后稳恒磁场高斯定理的学习和理工科专业后续专业课程（比如电子信息工程专业课《电磁场与波》的学习）中计算电场强度奠定了基础，学生通过学习该定理能掌握科学的思维方法和研究方法，体验物理学中的对称和谐之美。

（二）学生学习基础分析学生在学习本节之前，已掌握了利用库仑定律求解真空中静止点电荷周围的电场强度Ｅ，体会到利用该定律求解对数学尤其是积分运算要求较高且计算过程比较复杂，那么，求解带电体周围激发的静电场Ｅ是否还有其他相对简便的方法？静电场是否是有源场？这些都是要和学生共同解决的问题．更重要的是静电场和稳恒磁场的物理规律具有一定的对称性，静电场的学习将为后续稳恒磁场的学习做铺垫。

二、教学目标设计（一）知识与技能1、深刻理解电场强度Ｅ的闭合曲面积分（或Ｅ的通量）与该闭合面所包围电荷之间的关系；2、电通量概念的理解和正负的判断；3、对于多个点电荷或连续分布带电体周围激发的电场，理解闭合曲面上Ｅ的本质内涵及表达式中正负电荷表示；4、掌握选取适当高斯面的方法及积分技巧，了解定理求场强的适用条件，熟练应用定理解决轴对称、球对称、面对称性分布带电体周围的电场问题（二）过程与方法1、师生互动共同推导高斯定理的数学表达式，掌握从特殊到一般的科学研究方法．2、经历利用高斯定理解决实际物理问题的过程，强调该定理的适用范围和注意事项，情感态度与价值观。

高中物理高斯定理教案
主题：高斯定理
教学目标：
1. 了解高斯定理的基本概念和原理；
2. 掌握通过高斯定理计算电场的方法；
3. 能够应用高斯定理解决相关问题。

教学重点：
高斯定理的概念和原理；
通过高斯定理计算电场的方法。

教学难点：
应用高斯定理解决相关问题。

教学准备：
教材、投影仪、黑板、粉笔、实验器材等。

教学过程：
一、导入（5分钟）
教师通过提问、引入实例等方式引出高斯定理的概念，激发学生对物理学习的兴趣。

二、讲解高斯定理（15分钟）
1. 阐述高斯定理的基本概念和原理；
2. 引导学生理解高斯定理的含义；
3. 分析高斯定理在电场分析中的应用。

三、实验演示（15分钟）
教师进行实验演示，展示如何利用高斯定理计算电场。

四、小组讨论（15分钟）
学生分组讨论，解决使用高斯定理计算电场的练习题。

五、总结（5分钟）
教师总结本节课的内容，强调高斯定理的重要性和应用。

六、作业布置（5分钟）
布置相关作业，巩固学生对高斯定理的理解和应用能力。

教学反馈：
教师通过课堂讨论、作业完成情况等方式收集学生对高斯定理的掌握程度，及时调整教学方法，帮助学生更好地理解和应用高斯定理。

大学物理静电场(高斯定理)课件一、教学内容本节课的教学内容来自于大学物理的静电场部分，具体涉及高斯定理。

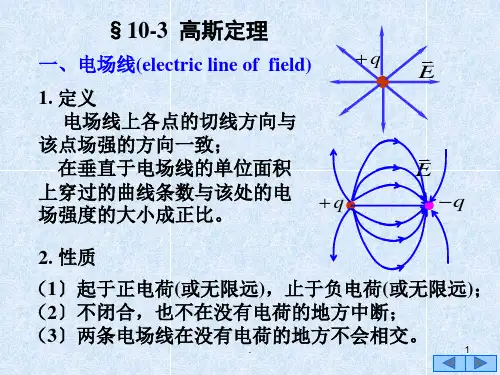
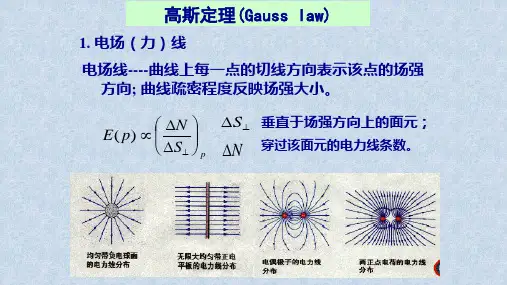
高斯定理是描述电场通过任意闭合曲面的电通量与该闭合曲面内部的电荷量之间的关系。

数学表达式为：\[ \oint_S \mathbf{E} \cdot d\mathbf{A} =\frac{Q}{\varepsilon_0} \]其中，\( \mathbf{E} \) 表示电场强度，\( d\mathbf{A} \) 表示曲面元素，\( Q \) 表示闭合曲面内部的电荷量，\( \varepsilon_0 \) 表示真空中的电常数。

二、教学目标1. 理解高斯定理的数学表达和物理意义。

2. 学会运用高斯定理计算闭合曲面内的电荷量。

3. 掌握高斯定理在实际问题中的应用。

三、教学难点与重点重点：高斯定理的数学表达和物理意义。

难点：如何运用高斯定理计算闭合曲面内的电荷量，以及高斯定理在实际问题中的应用。

四、教具与学具准备教具：投影仪、黑板、粉笔。

学具：笔记本、笔、计算器。

五、教学过程1. 实践情景引入：以雷电现象为例，介绍静电场中的电荷分布和电场强度。

引导学生思考如何计算一个闭合曲面内的电荷量。

2. 理论知识讲解：讲解高斯定理的数学表达和物理意义。

通过示例，解释高斯定理如何描述电场通过闭合曲面的电通量与内部电荷量之间的关系。

3. 例题讲解：给出一个具体的题目，指导学生如何运用高斯定理计算闭合曲面内的电荷量。

题目如下：一个半径为 \( R \) 的球体，在其表面分布着电荷，求球体内的电荷量。

4. 随堂练习：让学生独立完成上述题目的计算。

在课堂上选取几位学生的答案进行讲解和讨论。

5. 作业布置：布置一道类似的题目，要求学生课后完成。

题目如下：一个长方体导体，其两个相对面上分别分布着电荷 \( Q_1 \) 和\( Q_2 \)，求长方体内部的电荷量。

6. 板书设计：板书高斯定理的数学表达式和物理意义，以及解题步骤和关键点。