高斯定理例题

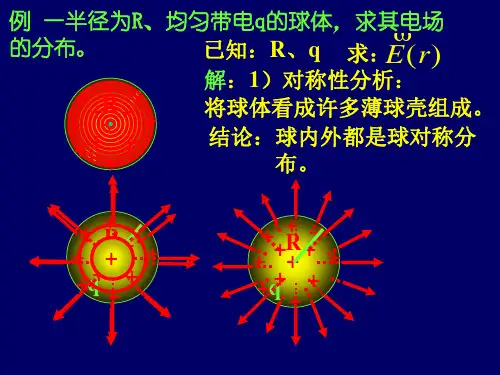
高斯公式经典例题好的，以下是为您生成的文章：在数学的奇妙世界里，高斯公式就像一把神奇的钥匙，能帮我们打开许多难题的大门。

今天咱们就一起来瞅瞅高斯公式的一些经典例题，感受感受它的魅力！我还记得之前有个学生小明，那叫一个苦恼啊。

每次遇到跟高斯公式相关的题目，就像霜打的茄子——蔫了。

有一次考试，考到了这么一道题：计算向量场 $\vec{F} = (x^2 + y^2 + z^2) \vec{i} + 2xy \vec{j} + 2xz \vec{k}$ 通过闭曲面 $S$ 所围成的区域 $V$ 的通量，其中 $S$ 是由球面 $x^2 + y^2 + z^2 = 1$ 所围成的闭曲面。

小明当时拿到这道题，脑子一片空白，完全不知道从哪儿下手。

这其实就是一个典型的可以用高斯公式解决的问题。

咱们先来说说高斯公式到底是啥。

简单来讲，高斯公式就是说，如果有一个空间闭区域 $V$ ，它是由闭曲面 $S$ 所围成的，函数 $P$ 、$Q$ 、 $R$ 及其一阶偏导数在 $V$ 上连续，那么就有 $\iiint_V(\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}) dV = \iint_S Pdydz + Qdzdx + Rdxdy$ 。

那咱们再回过头来看刚才那道题。

首先，得求出 $\frac{\partialP}{\partial x}$ 、 $\frac{\partial Q}{\partial y}$ 、 $\frac{\partialR}{\partial z}$ 。

经过一番计算，$\frac{\partial P}{\partial x} = 2x$ ，$\frac{\partial Q}{\partial y} = 2x$ ，$\frac{\partial R}{\partial z} = 2x$ ，所以 $\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} +\frac{\partial R}{\partial z} = 6x$ 。

四、计算题1、 两个无限大的平行平面都均匀带电，电荷的面密度分别为1σ和2σ，试求空间各处场强．两面间 , 1σ面外 , 2σ面外 . （填写A 、B 、C 或D ，从下面的选项中选取）A 、n E )(21210σσε-=B 、1201()E n σσε=+C 、n E)(21210σσε+-= D 、n E)(21210σσε+= 答案：A ，C ，D解: 如图所示，两带电平面均匀带电，电荷面密度分别为1σ与2σ，两面间， n E )(21210σσε-=1σ面外， n E)(21210σσε+-= 2σ面外， n E)(21210σσε+=n：垂直于两平面由1σ面指为2σ面．2、一无限长带电直线,电荷线密度为λ,傍边有长为a , 宽为b 的一矩形平面, 矩形平面中心线与带电直线组成的平面垂直于矩形平面，带电直线与矩形平面的距离为c ，如图，求通过矩形平面电通量的大小. . （填写A 、B 、C 或D ，从下面的选项中选取）A 、()0arctan 22a b c λπε⎡⎤⎣⎦B 、()0arctan 2a b c λπε⎡⎤⎣⎦ C 、()0arctan 24a b c λπε⎡⎤⎣⎦D 、()02arctan 2a b c λπε⎡⎤⎣⎦ 答案：Bab cλ解：取窄条面元adx ds =,该处电场强度为rE 02πελ=过面元的电通量为()220022cos xc acdxadx r s d E d e +=⨯=⋅=Φπελπεθλ ()⎰⎰-+=Φ=Φ2/2/2202b b e e xc acdxd πελ2/2/0arctan 12b b cxc ac -⋅=πελ()[]02arctan πελc b a =3、 如图所示，在x －y 平面内有与y 轴平行、位于x＝a / 2和x ＝-a / 2处的两条“无限长”平行的均匀带电细线，电荷线密度分别为＋λ和－λ．求z 轴上任一点的电场强度．. . （填写A 、B 、C 或D ，从下面的选项中选取）A 、()2204a i a z λπε-+B 、()22024a i a z λπε-+ C 、()22024a i a z λπε-+ D 、()22044a i a z λπε-+ 答案：C解：过z 轴上任一点(0 , 0 , z )分别以两条带电细线为轴作单位长度的圆柱形高斯面，如图所示．按高斯定理求出两带电直线分别在该处产生的场强大小为 ()r E 02/ελπ=± 场强方向如图所示． 按场强叠加原理，该处合场强的大小为r a r E E 2/cos 20⋅π==+ελθ ()22042z a a +π=ελ方向如图所示． 或用矢量表示 ()iz a a E 22042+π-=ελabcλxyE rθr O zxE E + E -θza/2 -a/2Oz xy-λλ-a/2a/24、均匀带电球壳内半径6cm ，外半径10cm ，电荷体密度为2×510-C·m -3求距球心5cm 的场强 ，8cm 的场强 ,12cm 的场强 . （填写A 、B 、C 或D ，从下面的选项中选取）．A 、43.4810⨯1C N -⋅， 方向沿半径向外 B 、44.1010⨯1C N -⋅ ,沿半径向外C 、44.1010⨯1C N -⋅,方向沿半径向外D 、 0 答案： D, A ，B解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=q r E当5=r cm 时，0=∑q ,0=E8=r cm 时，∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅， 方向沿半径向外． 12=r cm 时,3π4∑=ρq -3(外r ）内3r ∴ ()420331010.4π43π4⨯≈-=rr r E ερ内外 1C N -⋅ 沿半径向外.5、有两个半径分别为1R 、2R 的同心球壳，带电分别为1Q 、2Q ，试求空间电场分布。

简析高斯定理在电场中的应用高斯定理是物理学中电学部分的重要定理之一，在简化计算具有对称性的电场中有着重要应用，例如均匀带电的平面、直线、圆柱体、球面、球体等的电场的计算. 如果不理解高斯定理，不熟练掌握高斯定理的应用技巧，就会感到高斯定理深不可测. 下面，笔者就几年来的教学体会对高斯定理及其在电场中的应用作以简要分析.三、高斯定理在电场中的应用［例题1］设一块均匀带正电无限大平面，电荷密度为σ=9.3×10-8C/m 2，放置在真空中，求空间任一点的场强.解：根据电荷的分布情况，可作如下判断：(1)电荷均匀分布在均匀带电无限大平面上，我们知道孤立正的点电荷的电场是以电荷为中心，沿各个方向在空间向外的直线，因此空间任一点的场强只在与平面垂直向外的方向上(如果带负电荷，电场方向相反)，其他方向上的电场相互抵消；(2)在平行于带电平面的某一平面上各点的场强相等；(3)带电面右半空间的场强与左半空间的场强，对带电平面是对称的.为了计算右方一点A 的场强，在左取它的对称点B ，以AB 为轴线作一圆柱，如图-3所示. 对圆柱表面用高斯定理，图-3⎰∑=+=⋅=se e e q ds E 0εφφφ两个底面侧面 (1)0=侧e φ (2) ES e 2=两个底面φ (3)圆柱内的电荷量为∑=S q σ (4)把(2)、(3)、(4)代入(1)得02εσ=E =1281085.82103.9--⨯⨯⨯V/m=5.25×103 V/m ［例题2］设有一根无限长块均匀带正电直线，电荷线密度为λ=5.0×10-9C/m ，放置在真空中，求空间距直线1m 处任一点的场强.解：根据电荷的分布情况，可作如下判断：(1)电荷均匀分布在无限长块均匀直线上，我们知道孤立正的点电荷的电场是以电荷为中心，沿各个方向在空间向外的直线，因此空间任一点的场强只在与直线垂直向外的方向上存在(如果带负电荷，电场方向相反)，其他方向上的电场相互抵消；(2)以直线为轴线的圆柱面上各点的场强数值相等，方向垂直于柱面(如图-4).图-4根据场强的分布，我们以直线为轴作长为l ，半径为r 的圆柱体.把圆柱体的表面作为高斯面，对圆柱表面用高斯定理：⎰∑=+=⋅=se e e q ds E 0εφφφ两个底面侧面 (1)rlE E S e πφ2==侧侧 (2) 0=两个底面e φ (3)圆柱内的电荷量为∑=l q λ (4)把(2)、(3)、(4)代入(1)得r E 02πελ==11085.814.32100.5129⨯⨯⨯⨯⨯--V/m=89.96 V/m［例题3］设有一半径为R 的均匀带正电球面，电荷为q ，放置在真空中，求空间任一点的场强. 解：由于电荷均匀分布在球面上,因此,空间任一点P 的的场强具有对称性,方向由球心O 到P 的径矢方向(如果带负电荷，电场方向相反)，在与带电球面同心的球面上各点E 的大小相等.根据场强的分布，我们取一半径为r 且与带电球面同系同心的球面为为高斯面，如图-5所示.图-5若R r <，高斯面2S 在球壳内，对球面2S 用高斯定理得 ⎰∑=⋅=⋅=se q r E ds E 024επφ球内因为球壳内无电荷，∑=0q ，所以0=球内E若R r >，高斯面1S 在球壳外，对球面1S 用高斯定理得∑=q q ，故有24επqE R =204rq E πε=由此可知，均匀带电球面内的场强为零，球面外的场强与电荷集中在球心的点电荷所产生的场强相同.四、高斯定理在电场中的一般应用步骤: (1) 判断电场的分布特点；(2) 合理作出高斯面，使电场在其中对称分布；(3) 找出电场在高斯面内的垂直面积⊥S ； (4) 分析高斯面内的电荷量q ； (5) 应用高斯定理求解(⎰∑=⋅=ss e qds E 0)(εφ内).我们知道，用电场的叠加原理也可以计算连续分布的电荷所产生的场强，但是高斯定理以其简单明了的步骤最终赢得读者的喜爱.第四讲：高斯定理的应用高斯定理的一个重要应用，是用来计算带电体周围电场的电场强度。

一、选择题1．关于高斯定理的理解有下面几种说法，其中正确的是（ ）。

（A ）如果高斯面上E处处为零，则该面内必无电荷。

（B ）如果高斯面内无电荷，则高斯面上E 处处为零。

（C ）如果高斯面上E 处处不为零，则高斯面内必有电荷。

（D ）如果高斯面内有净电荷，则通过高斯面的电通量必不为零。

2．如右图所示，闭合面S 内有一点电荷q ，P 点为S 面上一点，在S 面外A 点处有一点电荷q ′，若将q ′移至B 点，则（ ）。

（A ）S 面的总电通量改变，P 点的场强不变。

（B ）S 面的总电通量不变，P 点的场强改变。

（C ）S 面的总电通量和P 点的场强都不改变（D ）S 面的总电通量和P 点的场强都改变3．如右图所示，半径为R 1的均匀带电球面1，带电量为Q 1，其外有一同心的半径为R 2的均匀带电球面2，带电量为Q 2，则离球心为r （R 1< r <R 2）处的某点P 的场强为（ ）。

（A ）r r Q E 2014πε= （B ）r rQ Q E 20214πε+= （C ）r r Q E 3014πε= （D ）r r Q Q E 30214πε+= 二、填空题1．如右图所示，三个平行的“无限大”均匀带电平面，其电荷面密度都是+σ，则A 、B 、C 、D 四个区域的电场强度分别为：A E = ，B E = ，C E = ，DE = ，（设方向向右为正）。

2．带电量分别为1q 和2q 的两个点电荷单独在空间各点建立的静电场分别为1E 和2E ，空间各点总场强为21E E E +=。

现在作一封闭曲面S ，如下图所示，则以下两式可分别求出通过S 的电通量：3．（1）点电荷q 位于一个边长为a 的立方体中心，试求在该点电荷电场中穿过立方体一面的电通量是 。

（2）如果将该场源点电荷移到立方体的的一个角上，这时通过立方体各面的电通量是 ； 。

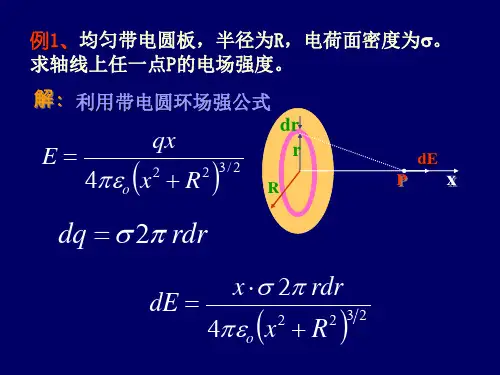
一 D B C二 1. 032A E σε=-，02B E σε=-02C E σε=032D E σε= 2.10q ε，20q ε 3，06q ε，024q ε，0三 计算题1．解：薄板可近似为带电面分析知，场强分布是面对称的，因而建立如图所示的关于薄板面对称的柱形高斯面，两个底面分别为S 1和S 2。

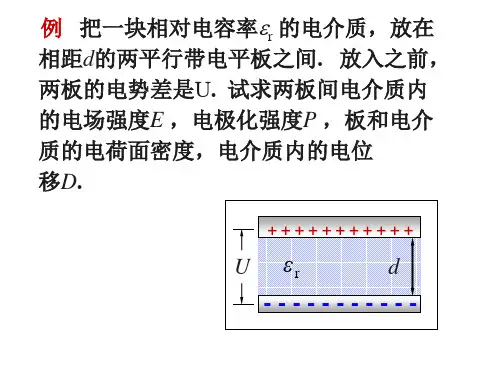
8-4 电位移 有电介质时的高斯定理在高斯面内不仅会有自由电荷，而且还会有极化电荷。

这时，高斯定理应有些什么变化呢？ 我们仍以在平行平板电容器中充满各向同性的均匀电介质为例来进行讨论。

在如下图所示的情形中，取一闭合的正柱面作为高斯面，高斯面的两端面与极板平行，其中一个端面在电介质内，端面的面积为S 。

设极板上的自由电荷面密度为0σ，电介质表面上的极化电荷面密度为σ'。

由高斯定理，有⎰'-=⋅sQ Q 00)(1d εS E （8-12）式中Q Q '和0分别为S Q S Q σσ'='= 00和。

我们不希望在式（8-12）中出现极化电荷，利用前节讨论的结果，我们可以计算出r 00/εQ Q Q ='- （8-13）把它代入（8-12）有⎰=⋅sQ r 00d εεS E或⎰=⋅sQr0d S E εε （8-14）现在不妨，令E E D εεε==r 0 （8-15）其中εεε=r 0叫做电介质的电容率。

那么式（8-14）可写成⎰=⋅sQd S D （8-16）式中D 称作电位移，而⎰⋅sSD d 则是通过任意闭合曲面S 的电位移通量。

D 的单位为2m C -⋅讨论：证明:关于r Q Q Q ε00='-的证明电介质中的电场强度E 应为E E E '+=0考虑到E '的方向与0E 的方向相反，以及E 与E '的关系式（8-9），可得电介质中电场强度E 的值为r 00εE E E E ='-=故rr 1E E εε-='因为 0/εσ'='E ，000/εσ=E从而可得0rr 1σεεσ-='由于S Q 00σ=、S Q σ'='，故上式亦可写成rr 1Q Q εε-='即r Q Q Q ε00='-式（8-16）虽是从平行板电容器得出的，但可以证明在一般情况下它也是正确的。

高斯定律测试题高斯定律是电学中的基本定律之一，描述了电场与电荷之间的关系。

本文将通过一系列测试题来检验读者对高斯定律的理解和应用能力。

第一题：一个半径为R的球面上有一个总电荷量为Q的点电荷，求球面上的电场强度E。

解析：根据高斯定律，通过封闭曲面的电场通量等于封闭曲面内的电荷总量除以真空介电常数：∮E·dA = Q/ε0。

对于球面来说，曲面上的dA与电场强度E的方向垂直，因此，等式化简为E·4πR² = Q/ε0，解得E = Q/4πε0R²。

第二题：一段长度为L的直导线在其上按匀布电荷线分布，每单位长度为λ，求该导线附近的电场强度E。

解析：使用高斯定律，以导线为轴线，取一个长为L、半径为r的圆柱面作为高斯面。

根据题意，匀布电荷线分布对应着电荷线密度λ，因此高斯面内的总电荷量为Q = λL。

根据高斯定律，E·2πrL = λL/ε0，解得E = λ/2πrε0。

第三题：一个无限长直导线的线外、线内电场强度分别为E₁和E₂，两者的比值是多少？解析：以导线为轴线，在线外取一个圆柱面作为高斯面，此高斯面通过线外无限远处。

根据高斯定律，通过高斯面的电场通量为0，因此高斯面内的总电荷量为0。

由于高斯面内不含电荷，故曲面上的电场强度E₁与E₂相等。

即 E₁/E₂ = 1/1 = 1。

通过以上的测试题，我们对高斯定律的应用能力进行了检验，相信读者对高斯定律有了更深入的理解。

不同形式的高斯面可以帮助我们求解不同情况下的电场强度分布，通过理解和应用高斯定律，我们可以更好地理解电荷与电场之间的相互作用。

继续学习和掌握电学知识，将有助于我们在实际问题中解决各种电场相关的计算和应用。

四年级数学高斯定理练习题高斯定理（也称为散度定理）是向量微积分中的一个重要定理，它与流量有关。

在本文中，我们将通过一些四年级数学的高斯定理练习题来帮助学生更好地理解和应用这个定理。

1. 题目一：一个长方体的六个面分别是ABCD、ABFE、BCGF、ADHE、CDHG和EFHG，其中AB = 3 cm，BC = 4 cm，AD = 5 cm。

求这个长方体的表面积。

解析：根据高斯定理，这个长方体的表面积等于通过每个面的流量之和。

由于长方体是闭合的，我们可以将它看作一个整体，那么通过每个面的流量都可以表示为1。

所以，这个长方体的表面积等于6个面的流量之和，即6。

答案：6。

2. 题目二：一个球体的表面被一个平面切割成两个部分，其中一个部分的面积为16π，求另一个部分的面积。

解析：根据高斯定理，球体的表面积等于通过每个表面的流量之和。

由于球体是闭合的，我们可以将它看作一个整体，那么通过每个表面的流量都可以表示为1。

所以，这个球体的表面积等于2个部分的流量之和。

已知一个部分的面积为16π，那么另一个部分的面积就是球体的表面积减去已知部分的面积，即2-16π。

答案：2-16π。

3. 题目三：一根长为10 cm、宽为4 cm、高为6 cm的长方体块状物质，它的两个对角线分别与X轴、Y轴和Z轴平行。

求这个块状物质的体积。

解析：根据高斯定理，块状物质的体积等于通过每个面的流量之和。

由于块状物质是闭合的，我们可以将它看作一个整体，那么通过每个面的流量都可以表示为1。

所以，这个块状物质的体积等于6个面的流量之和，即6。

答案：6。

4. 题目四：一个立方体的边长为2 cm，内部充满了水。

求在一个单位时间内，通过立方体表面的水流量。

解析：根据高斯定理，通过立方体表面的水流量等于立方体内部的流量。

由于立方体是闭合的，我们可以将它看作一个整体，那么通过每个面的流量都可以表示为1。

所以，通过立方体表面的水流量等于立方体内部的流量，即1。