一阶RC电路的暂态响应
- 格式:doc
- 大小:5.41 MB
- 文档页数:11

实验报告课程名称:电路与电子实验I 指导老师:童梅成绩:__________________ 实验名称:一阶RC电路的暂态响应实验类型:电路实验同组学生姓名:一、实验目的二、实验原理三、实验接线图四、实验设备五、实验步骤六、实验数据记录七、实验数据分析八、实验反思九、仿真部分一、实验目的:1.熟悉一阶RC电路的零状态响应、零输入响应和全响应;2.研究一阶电路在阶跃激励和方波激励情况下,响应的基本规律和特点;3.从响应曲线中求出RC电路时间常数;4.掌握积分电路和微分电路的基本概念。
二、实验原理:1.零输入响应:无外施激励,即输入信号为零,由储能元件的初始储能所引起的响应。
在零输入响应中,U c(0-)=U0,U c=U0*e-t/RC,i=I0*e-t/RC,令τ=RC,称其为一阶电路的时间常数。
如图,令t2-t1=τ,则U c(t2)=e-1*U0*e-t/τ=0.368U c(t1),先在起始点附近确定一点U1,然后确定U2=0.368U1,即U1-U2=0.632U1,然后利用示波器的光标追踪来寻找U2,二者对应的横坐标为t1、t2,τ=t2-t1。
2.零状态响应:换路前储能元件没有初始储能,由外施激励所产生的响应。
在零状态响应中,U c=U s(1-e-t/RC),i=U s/R*e-t/RC,τ=RC为时间常数。
如图,令t2-t1=τ,则U c(t2)=U s(1-0.368e-t1/τ),则U c(t2)-U c(t1)=0.632(U s-U c(t1)),在起始点附近确定一点U1,再通过 U c(t2)-U c(t1)=0.632(U s-U c(t1))确定U2,二者的横坐标分别为t1、t2,τ=t2-t1。
3.全响应状态:外施激励和初始状态共同作用下产生的电路响应。
全响应=零状态响应+零输入响应三者的图像如下:4.方波响应:从本质上看,方波是以相同的时间间隔,不停开关的电压。

一阶RC电路的暂态响应一、实验目的1、观察RC电路的充放电过程及其与时间常数的关系。
2、在微分电路和积分电路中,时间常数与工作脉冲宽度对输出波形的影响。
3、学习低频信号发生器及示波器的使用。
二、实验设备双踪示波器低频信号发生器电工电路基本模块系统三、实验内容说明1、微分电路微分电路在脉冲技术中有着广泛的应用。
图1所示为微分电路,其输出电压u o为:u o=Ri=Rc du c/dt,即输出电压u o与电容两端电压u c对时间的导数成正比。
当电路的时间常数τ=RC很小时,u c»u,则u i=u c+u o≈u c,∴uo≈RCdu i/dt。
图1微分电路原理图即当时间常数τ=RC很小时,输出电压uo近似与输入电压对时间的导数成正比。
所以图1电路称为“微分电路”。
图1所示电路并不是在任何条件下都能起微分作用的。
有无微分作用的关键是时间常数τ与脉冲宽度tp的相对大小。
当τ<<tp时,微分作用显著,输出电压成为双向的尖脉冲,如图2(a)所示。
当τ=tp时,微分作用不显著[见图2(b)]。
当τ>>tp时,输出电压uo的波形基本上与输入电压u i的波形一致,只是将波形向下平移了一段距离,使波形正半周和负半周所包含的面积相等[见图2(c)]。
这时电路成为一般阻容耦合电路。
ui uo tuo ui ui 0t 0t0ttp ←T →00t (a)τ=tp (b)τ=tp (c)τ>>tp图2不同时间常数对微分电路输出波的影响2、积分电路将图1中的R ﹑C 的位置对换,便成图3所示的积分电路。
此时输出电压U o 为即输出电压Uo 与电阻两端电压U R 对时间的积分成正比。
当电路的时间常数τ=RC 很大时,U R >>U 0,则Ui=U R +U 0≈U R ,∴即当τ很大时,输出电压Uo 近似与输入电压Ui 对时间的积分成正比。
所以图3电路称为“积分电路”。

一阶rc电路的暂态响应实验报告分析
一阶rc电路的暂态响应实验报告分析
本文为大家带来一阶rc电路的暂态响应实验报告分析。
实验内容和原理
1、零输入响应:指输入为零,初始状态不为零所引起的电路响应。
2、零状态响应:指初始状态为零,而输入不为零所产生的电路响应。
?
3、完全响应:指输入与初始状态均不为零时所产生的电路响应。
操作方法和实验步骤
1、利用Multisim软件仿真,了解电路参数和响应波形之间的关系,并通过虚拟示波器的调节熟悉时域测量的基本操作。
2、实际操作实验。
积分电路和微分电路的电路接法如下,其中电压源使。

一阶RC电路的暂态响应实验报告本次实验的目的是研究一阶RC电路的暂态响应,了解RC电路在电路中的应用及其响应特性,并通过实验观察、测量一阶RC电路的电流和电压随时间变化的情况,掌握实验技能和数据处理方法。
实验器材:- 万用表- 脉冲信号发生器- 电容- 电阻实验步骤:1. 根据电路图连接电路,将电容和电阻连接成一阶RC电路,通过脉冲信号发生器产生一个方波信号,调节频率为50Hz、幅值为10V。
2. 用万用表测量R、C的阻值和电容器的标称电容。
3. 用示波器观察方波信号波形,调整脉冲信号发生器的输出幅值和偏置电压,确保方波的基准线为0V。
4. 连接万用表,分别测量电容器两端的电压、电阻上的电压和电流,记录每一次测量的时间,以及电流和电压的数值,根据实验数据绘制电流和电压随时间变化的波形图。
实验结果:实验记录了电容器两端电压、电阻上的电压和电流随时间的变化情况,记录的数据如下:| 时间(ms) | Uc(V) | UR(V) | I(mA) || ---------- | ------- | ------- | ------- || 0 | 0 | 10 | 0 || 1 | 3.95 | 6.05 | 3.55 || 2 | 6.3 | 3.7 | 2.72 || 3 | 7.87 | 2.13 | 2.05 || 4 | 8.95 | 1.05 | 1.57 || 5 | 9.6 | 0.4 | 1.2 || 6 | 9.87 | 0.13 | 0.94 || 7 | 9.96 | 0.04 | 0.74 || 8 | 10 | 0 | 0.59 |结论:根据实验数据绘制的电流和电压随时间变化的波形图可以发现,电容器的电压随时间的增加而增加,最终趋近于直流源的电压值,而电阻上的电压随时间的增加而减小,最终趋近于0V。
同时,电流随时间的增加而减小,也趋近于0A。
这种响应特性是一阶RC电路的典型特征,称为指数衰减响应。

一阶RC电路的暂态响应实验报告仿真实验 1 一阶RC电路的暂态响应一、实验目的1.熟悉一阶 RC电路的零状态响应、零输入响应和全响应;2.研究一阶电路在阶跃激励和方波激励情况下,响应的基本规律和特点;3.掌握积分电路和微分电路的基本概念;4.研究一阶动态电路阶跃响应和冲激响应的关系;5.从响应曲线中求出 RC 电路的时间常数τ。
二、实验原理1、零输入响应(RC 电路的放电过程):2、零状态响应(RC 电路的充电过程)3.脉冲序列分析(a) τ <<t< p="">(b) τ >T三、主要仪器设备1.信号源2.动态实验单元DG083.示波器四、实验步骤RC 充放1.选择 DG08 动态电路板上的 R、C 元件,令R=1k Ω,C=1000 μF 组成如图所示的电电路,观察一阶 RC 电路零状态、零输入和全响应曲线。
2.在任务 1 中用示波器测出电路时间常数τ,并与理论值比较。
3.选择合适的R 和 C 的值(分别取R=1K Ω ,C=0.1μF; R=10K Ω ,C=0.1 μ F 和R=5 K Ω ,C=1μF),连接 RC 电路,并接至幅值为3V , f=1kHz 的方波电压信号源,利用示波器的双踪功能同时观察 U c、 U R波形。
4.利用示波器的双踪功能同时观察阶跃响应和冲激响应的波形。
五、实验数据记录和处理一阶电路的零输入响应。
一阶电路的零状态响应从图中可以看出电路的时间常数τ = x=1.000s一阶电路的全响应方波响应(其中蓝线表示U c ,绿线表示 U R )τ =0.1T时放大后τ=1T 时τ=10T 时阶跃响应和冲激响应</t<>。

一阶rc暂态电路的暂态过程实验报告1. 了解RC电路的基本原理;2. 学习使用示波器观察RC电路的暂态响应过程;3. 通过实验验证RC电路的暂态响应公式。
实验器材:1. 信号发生器;2. 数字示波器;3. 电阻箱;4. 电容器。
实验原理:一阶RC电路是由一个电容和一个电阻串联组成的电路,其电路图如下所示: = V0 ×(1 - e-t/RC)其中,V0为初始电压,t为时间,R为电阻值,C为电容值。
实验步骤:1. 按照电路图搭建RC电路,调节电阻箱和电容器,使得其电路参数符合要求;2. 将示波器的通道1接到电容器上,将通道2接到信号发生器的输出端口;3. 设置信号发生器的正弦波频率为1000Hz,幅值为5V,接通电路;4. 在示波器上观察RC电路的暂态响应过程,并记录观察结果;5. 重新设置信号发生器的正弦波频率为2000Hz,重复步骤4,并记录观察结果。
实验结果:1. 当信号发生器的正弦波频率为1000Hz时,示波器上的V-t曲线如下所示:
4.5 一阶RC 电路的暂态过程分析一、实验目的1.学习用示波器观察和分析RC 电路的响应。
2.了解一阶RC 电路时间常数对过渡过程的影响,掌握用示波器测量时间常数。
3.进一步了解一阶微分电路、积分电路和耦合电路的特性。
二、实验原理1.一阶RC 电路的全响应=零状态响应+零输入响应。
当一阶RC 电路的输入为方波信号时,一阶RC 电路的响应可视为零状态响应和零输入响应的多次重复过程。
在方波作用期间,电路的响应为零输入响应,即为电容的充电过程;在方波不作用期间,电路的响应为零输入响应,即为电容的放电过程。
方波如图4.5.1所示。
图4.5.1 方波电压波形 图4.5.4 测常数和积分电路接线2.微分电路如图4.5.2所示电路,将RC 串联电路的电阻电压作为输出U 0,且满足τ ‹‹ t w 的条件,则该电路就构成了微分电路。
此时,输出电压U 0近似地与输入电压U i 呈微分关系。
dt du RC U i O 图4.5.2 微分电路和耦合电路接线 图4.5.3 微分电路波形微分电路的输出波形为正负相同的尖脉冲。
其输入、输出电压波形的对应关系如图4.5.3所示。
在数字电路中,经常用微分来将矩形脉冲波形变换成尖脉冲作为触发信号。
3.积分电路积分电路与微分电路的区别是:积分电路取RC 串联电路的电容电压作为输出U 0,如图4.5.4所不电路,且时间常数满τ ››t w 。
此时只要取τ=RC ››t w ,则输出电压U 0近似地与输入电压U i 成积分关系,即⎰≈t i O d u RC U 1积分电路的输出波形为锯齿波。
当电路处于稳态时,其波形对应关系如图3.5.5所示。
注意:U i 的幅度值很小,实验中观察该波形时要调小示波器Y 轴档位。
图4.5.5 积分电路波形 图4.5.6 耦合电路波形4.耦合电路RC 微分电路只有在满足时间常数τ=RC ‹‹ t w 的条件下,才能在输出端获得尖脉冲。
如果时间常数τ=RC ››t w ,则输出波形已不再是尖脉冲,而是非常接近输出电压U i 的波形,这就是RC 耦合电路,而不再是微分电路。

课程名称: 电路与电子技术实验Ⅰ 指导老师: 成绩:______________实验名称: 一阶RC 电路的暂态响应 实验类型:基础规范型实验 同组学生姓名: 一、实验目的和要求(必填) 二、实验内容和原理(必填) 三、主要仪器设备(必填) 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析(必填) 七、讨论、心得一、实验目的与要求1.熟悉一阶RC 电路的零状态响应、零输入响应和全响应。
2.研究一阶电路在阶跃激励和方波激励情况下,响应的基本规律和特点。
3.掌握积分电路和微分电路的基本概念。
4.学习从响应曲线中求出RC 电路时间常数τ。
二、实验内容和原理1.零输入响应、零状态响应、全响应零输入响应:指激励为零,初始状态不为零所引起的电路响应。
零状态响应:初始状态为零,而激励不为零所产生的电路响应。
全响应:激励与初始状态均不为零时所产生的电路响应。
2.一阶RC 电路的零输入响应(放电过程) 如图,当开关闭合时,电路中有:)0()(0+-≥=t eU t u RCt C ; )0(-)(0R +-≥=t eU t u RCt)0(RU -)()(0C +-≥==t e R t u t i RC tR变化曲线如图所示,其中时间常数τ可通过以下方法求得:①按照时间常数的定义,τ即为右图中线段AB 。
②如图,在 [t0,uC(t0)]点作uC(t0)的切线,得到次切距CD ,线段CD 即为τ。
3. 一阶RC 电路的零状态响应(充电过程) 如上图,当开关断开时,电路中有:)0()(S +-≥-=t eU U t u RCt S C)0()(-)(C R +-≥==t eU t u U t u RCt S S)0(RU )()(S C +-≥==t e R t u t i RC tR变化曲线如图,计算τ的方法与零输入响应相同。
4.方波响应当方波信号激励加到RC 两端时,只要方波的半周期远大于电路的时间常数,就可以认为方波的上升沿或下降沿到来时,前一边沿所引起的过渡过程已经结束。
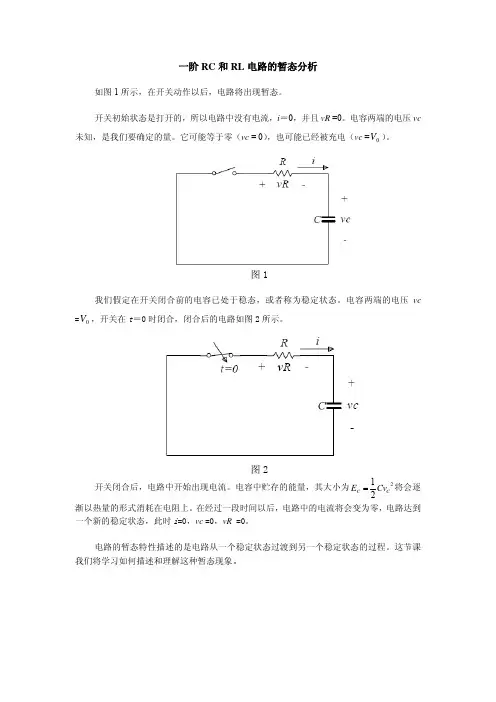
一阶RC 和RL 电路的暂态分析如图1所示,在开关动作以后,电路将出现暂态。
开关初始状态是打开的,所以电路中没有电流,i =0,并且vR =0。
电容两端的电压vc 未知,是我们要确定的量。
它可能等于零(vc = 0),也可能已经被充电(vc =)。
0V图1我们假定在开关闭合前的电容已处于稳态,或者称为稳定状态。
电容两端的电压vc =,开关在t =0时闭合,闭合后的电路如图2所示。
0V图2开关闭合后,电路中开始出现电流。
电容中贮存的能量,其大小为221C C Cv E =将会逐渐以热量的形式消耗在电阻上。
在经过一段时间以后,电路中的电流将会变为零,电路达到一个新的稳定状态,此时i =0,vc =0,vR =0。
电路的暂态特性描述的是电路从一个稳定状态过渡到另一个稳定状态的过程。
这节课我们将学习如何描述和理解这种暂态现象。
RC 电路的零输入响应我们首先研究零输入的RC 电路, 如图3所示。
图3我们假定电容是理想的,而且电容两端的电压在开关动作之前已经被充电至。
在t =0时,开关闭合。
电路中开始出现电流,在t >0时,我们得到的电容两端电压是一个关于时间t 的函数。
因为电容两端的电压应该是连续的,所以在时,=。
00V vc t =−=c v +=0t c v 0V我们首先要做的是得到这个电路的特性方程,可以通过基尔霍夫定律求解。
这里我们使用基尔霍夫电压定律:0)()(=+t v t v c R (0.1)由电阻以及电容的电压电流关系,可得方程0)()(=+t v dtt dv RCc c (0.2) RC 与时间具有同样的单位,即(Ohm )(Farad )→seconds (s F =•Ω)。
RC 称为电路的时间常数,通常用τ来表示,即RC =τ。
式(0.2)与电路的初始状态有关,电容初始电压00V vc t ==决定了电路在t >0时的特性。
实际上,由于电路中没有任何电源作用,所以这种特性也叫做电路的自然响应。

《电路与模电》实验报告实验题目:RC 一阶电路的暂态响应姓名: 学号: 实验时间: 实验地点: 指导老师: 班级:一、实验目的1.测定RC 一阶电路的零输入响应、零状态响应和全响应。
2.学习时间常数的测量方法。
3.掌握有关微分电路、积分电路的概念。
4.进一步学会用示波器观测波形。
二、实验原理1. 动态电路的过渡过程是十分短暂的单次变化过程,对时间常数τ较大的电路,可用慢扫描长余辉示波器观察光点移动的轨迹。
如果用一般的双踪示波器观察过渡过程和测量有关的参数,必须使这种单次变化的过程重复出现。
为此,可利用信号发生器输出的方波来模拟阶跃激励信号,即令方波输出的上升沿作为零状态响应的正阶跃激励信号;方波下降沿作为零输入响应的负阶跃激励信号,只要选择方波的重复周期远大于电路的时间常数τ那么电路在这样的方波序列脉冲信号的激励下,它的响应和直流接通与断开的过渡过程是基本相同的。
2. RC 一阶电路的零输入响应和零状态响应分别按指数规律衰减和增长,其变化的快慢决定于电路的时间常数τ3. 时间常数τ的测定方法:用示波器测得零状态响应的波形如图6-1所示。
根据一阶微分方程的求解得知 当零状态响应波形增长到0.632E 所对应的时间就等于τ。
τtRCt c EeEeu --==装订线图6-1 RC 电路的零状态响应亦可用零输入响应波形所对应的时间测得,如右下图所示。
图6-2 RC 电路的零输入响应当t =τ时,Uc(τ)=0.368E,此时所对应的时间就等于τ。
1. 微分电路和积分电路是RC 一阶电路中较典型的电路, 它对电路元件参数和输入信号的周期有着特定的要求。
一个简单的 RC 串联电路,在方波序列脉冲的重复激励下,当满足条件时(T 为方波脉冲的重复周期),且由R 端作为响应输出(如图6-3所示),则该电路就成了一个微分电路,因为此时电路的输出信号电压基本与输入信号电压的微分成正比。
利用微分电路可将方波转变成尖脉冲。
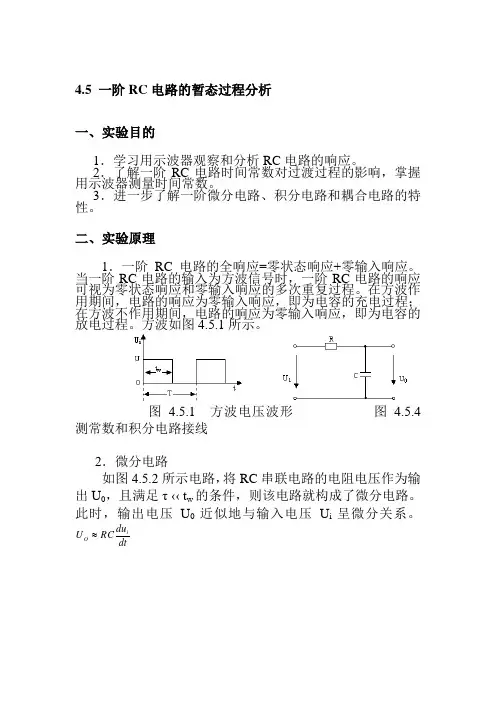
4.5 一阶RC 电路的暂态过程分析一、实验目的1.学习用示波器观察和分析RC 电路的响应。
2.了解一阶RC 电路时间常数对过渡过程的影响,掌握用示波器测量时间常数。
3.进一步了解一阶微分电路、积分电路和耦合电路的特性。
二、实验原理1.一阶RC 电路的全响应=零状态响应+零输入响应。
当一阶RC 电路的输入为方波信号时,一阶RC 电路的响应可视为零状态响应和零输入响应的多次重复过程。
在方波作用期间,电路的响应为零输入响应,即为电容的充电过程;在方波不作用期间,电路的响应为零输入响应,即为电容的放电过程。
方波如图4.5.1所示。
图 4.5.1 方波电压波形 图 4.5.4测常数和积分电路接线2.微分电路如图4.5.2所示电路,将RC 串联电路的电阻电压作为输出U 0,且满足τ ‹‹ t w 的条件,则该电路就构成了微分电路。
此时,输出电压U 0近似地与输入电压U i 呈微分关系。
dt du RC U i O图 4.5.2 微分电路和耦合电路接线 图4.5.3 微分电路波形微分电路的输出波形为正负相同的尖脉冲。
其输入、输出电压波形的对应关系如图4.5.3所示。
在数字电路中,经常用微分来将矩形脉冲波形变换成尖脉冲作为触发信号。
3.积分电路积分电路与微分电路的区别是:积分电路取RC 串联电路的电容电压作为输出U 0,如图4.5.4所不电路,且时间常数满τ ››t w 。
此时只要取τ=RC ››t w ,则输出电压U 0近似地与输入电压U i 成积分关系,即⎰≈ti O d u RC U 1 积分电路的输出波形为锯齿波。
当电路处于稳态时,其波形对应关系如图3.5.5所示。
注意:U i 的幅度值很小,实验中观察该波形时要调小示波器Y 轴档位。
图 4.5.5 积分电路波形 图 4.5.6耦合电路波形4.耦合电路 RC 微分电路只有在满足时间常数τ=RC ‹‹ t w 的条件下,才能在输出端获得尖脉冲。
如果时间常数τ=RC ››t w ,则输出波形已不再是尖脉冲,而是非常接近输出电压U i 的波形,这就是RC 耦合电路,而不再是微分电路。
实验4 一阶RC电路的暂态响应1.掌握电容器充电与放电过程中电流与电压的变化规律。
2.了解电路参数对充放电过程的影响。
3.了解微分电路与积分电路的功能及电路时间常数的选择方法。
1.电容器的充电、放电电容器是一种贮能元件,在带有电容器的电路中发生通断换接时,由于电容器贮能状态不能突变所以在电路中就产生了过渡过程。
在直流电路中,电容器接通电源,在极板上积累电荷的过程称为充电;已充电的电容器通过电阻构成闭合回路使电荷中和消失的过程称为放电。
根据电路理论,在单一贮能元件组成的一阶电路中,过渡过程中的暂态电流与电压是按指数规律变化的。
这一规律可以用下面的数字式表示,即τtc c c c ei i i t i −+∞−+∞=)]()0([)()(τtc c c c e u u u t u −+∞−+∞=)]()0([)()(式中及是起始瞬间的电容电流及电压,(0)C i +(0)C u +()C i ∞及()C u ∞是电路稳定后的电容电流及电压。
i RC图 3.4a.1 电容器充放电电路电容器充放电电路中电流、电压变化曲线分别如图3.4a.2(a)及图3.4a.2(b)所示。
这曲线是由电路发生通断瞬间的起始状态向新的稳定状态过渡的指数曲线。
其起始状态可根据换路定律确定,即在电路参数不变时,若电路发生换接,则电容器端电压不能突变,也就是在电路换接前后的瞬间是相等的,即c u )0()0(−+=c c u u电路的时间常数τ,可以根据和计算,即R C RC τ=,τ用来表征过渡过程的长短。
τ大过渡过程时间长,反之就短。
若的单位为Ω,C 的单位为F,则τ的单位为s。
Rτ可以从的变化曲线上求得。
从曲线上任选一点起算,每经过t =τ的时间,电流或电压就变化了起算值与稳态值之差的63.2%,即尚余36.8%需在以后过程中完成。
或者可在起算点作指数曲线的切线,此切线与稳态值坐标线的交点与起算点之间的时间坐标差即为时c u间常数。
实验八 RC 一阶电路的响应一、实验目的1、研究RC 电路在零输入、阶跃激励和方波激励情况下,响应的基本规律和特点。
2、学习用示波器观察分析电路的响应。
二、原理及说明1、一阶RC 电路对阶跃激励的零状态响应就是直流电源经电阻R 向C 充电。
对于图8-1所示的一阶电路,当t=0时开关K 由位置2转到位置1,由方程:C C S duU RC U dt+= 0t ≥初始值: ()00C u -= 可得出电容和电流随时间变化的规律:()1t C S U t U e τ-⎛⎫=- ⎪⎝⎭0t ≥ ()tS U i t e Rτ-= 0t ≥上述式子表明,零状态响应是输入的线形函数。
其中τ=RC ,具有时间的量纲,称为时间常数,它是反映电路过渡过程快慢程度的物理量。
τ越大,暂态响应所待续的时间越长。
反之,τ越小,过渡过程的时间越短。
图8-12、电路在无激励情况下,由储能元件的初始状态引起的响应称为零输入响应。
即电容器的初始电压经电阻R 放电。
在图8-1中,让开关K 于位置1,使初始值U C (0-)=U 0,再将开关K 转到位置2。
电容器放电由方程:0C C duU RC dt+= 0t ≥ 可以得出电容器上的电压和电流随时间变化的规律:()()0tC C u t u e τ--= 0t ≥()()0tC C u eu t Rτ--=-0t ≥3、对于RC 电路的方波响应,在电路的时间常数远小于方波周期时,可以视为零状态响应和零输入响应的多次过程。
方波的前沿相当于给电路一个阶跃输入,其响应就是零状态响应,方波的后沿相当于在电容具有初始值U C (0-)时把电源用短路置换,电路响应转换成零输入响应。
由于方波是周期信号,可以用普通示波器显示出稳定的图形,以便于定量分析。
本实验采用的方波信号的频率为1000Hz 。
三、仪器设备 PC 机、Multisim10.0; 四、实验方法:1、 打开Multisim10软件:开始—>程序—>National Instruments —>Circuit Design Suite 10.0 —〉Multisim图8-22、绘制电路图(1)、单击工具栏的:Place Basic 按钮弹出如下对话框:图8-3 电阻示波器、仪表电源库Place SourceRun基本元件库:Place Basic图8-4 电容图8-5 单刀双掷开关单击工具栏的:Place Source 按钮弹出如下对话框:图8-6 12V 直流稳压电源图8-7 方波信号源1、RC电路充电●按图8-8接线。
一阶电路暂态过程的研究实验报告一、实验目的1、观察一阶电路中电阻、电容和电感在接通和断开电源时的暂态过程,理解其物理现象。
2、学习使用示波器测量一阶电路的暂态响应,掌握示波器的基本操作。
3、研究一阶电路中时间常数对暂态过程的影响,加深对时间常数的理解。
4、通过实验数据的分析和处理,验证一阶电路暂态过程的理论。
二、实验原理一阶电路是指可以用一阶微分方程来描述的电路,通常包含一个储能元件(电容或电感)和一个耗能元件(电阻)。
在一阶电路中,当电路的结构或参数发生变化时(如电源的接通或断开),电路会经历一个暂态过程,然后达到一个新的稳态。
(一)一阶 RC 电路的暂态过程对于一阶 RC 串联电路,当开关 S 闭合时,电源通过电阻 R 向电容C 充电,电容两端的电压逐渐上升,直到达到电源电压。
其充电过程的电压表达式为:\(u_C(t) = U(1 e^{\frac{t}{RC}})\)其中,\(U\)为电源电压,\(R\)为电阻值,\(C\)为电容值,\(t\)为时间,\(RC\)称为时间常数,用\(\tau\)表示。
当开关 S 断开时,电容 C 通过电阻 R 放电,电容两端的电压逐渐下降,其放电过程的电压表达式为:\(u_C(t) = Ue^{\frac{t}{RC}}\)(二)一阶 RL 电路的暂态过程对于一阶 RL 串联电路,当开关 S 闭合时,电源通过电阻 R 向电感L 充电,电感中的电流逐渐上升,直到达到稳定值。
其充电过程的电流表达式为:\(i_L(t) =\frac{U}{R}(1 e^{\frac{Rt}{L}})\)其中,\(U\)为电源电压,\(R\)为电阻值,\(L\)为电感值,\(t\)为时间,\(\frac{L}{R}\)称为时间常数,用\(\tau\)表示。
当开关 S 断开时,电感 L 通过电阻 R 放电,电感中的电流逐渐下降,其放电过程的电流表达式为:\(i_L(t) =\frac{U}{R}e^{\frac{Rt}{L}}\)三、实验设备与器材1、示波器2、函数信号发生器3、直流电源4、电阻箱5、电容箱6、电感箱7、导线若干四、实验步骤(一)一阶 RC 电路暂态过程的研究1、按照电路图连接一阶 RC 串联电路,其中电阻\(R\)取\(100\Omega\),电容\(C\)取\(10\mu F\)。
一阶电路的暂态响应实验报告一、实验目的1、研究一阶 RC 电路和一阶 RL 电路的暂态响应特性。
2、观察时间常数对暂态过程的影响。
3、掌握用示波器测量暂态响应的方法。
二、实验原理1、一阶 RC 电路的暂态响应当一阶 RC 电路接通直流电源时,电容会充电;当电路断开直流电源时,电容会放电。
充电和放电过程都是暂态过程,其时间常数τ =RC 。
充电时,电容电压 uc 随时间按指数规律上升;放电时,电容电压 uc 随时间按指数规律下降。
2、一阶 RL 电路的暂态响应一阶 RL 电路在接通或断开直流电源时,电感电流 iL 会发生暂态变化。
时间常数τ = L/R 。
接通电源时,电感电流 iL 按指数规律上升;断开电源时,电感电流 iL 按指数规律下降。
三、实验仪器与设备1、示波器2、函数信号发生器3、直流稳压电源4、电阻、电容、电感等元件5、实验面包板6、连接导线若干四、实验内容与步骤1、一阶 RC 电路的暂态响应实验(1)按图 1 连接一阶 RC 充电电路,其中 R =10 kΩ,C =01 μF 。
(2)将直流稳压电源输出调至 10 V ,接入电路,用示波器观察并记录电容电压 uc 的充电过程。
(3)改变电阻 R 的值为20 kΩ ,重复上述实验。
(4)按图 2 连接一阶 RC 放电电路,电容预先充电至 10 V 。
(5)用示波器观察并记录电容电压 uc 的放电过程。
(6)改变电容 C 的值为02 μF ,重复上述放电实验。
2、一阶 RL 电路的暂态响应实验(1)按图 3 连接一阶 RL 充电电路,其中 R =100 Ω ,L = 100mH 。
(2)将直流稳压电源输出调至 5 V ,接入电路,用示波器观察并记录电感电流 iL 的充电过程。
(3)改变电阻 R 的值为200 Ω ,重复上述实验。
(4)按图 4 连接一阶 RL 放电电路,电感预先充电至一定电流值。
(5)用示波器观察并记录电感电流 iL 的放电过程。
一阶R C电路的暂态
响应
专业:电子信息技术及仪器
姓名:__黄云焜__________
实验报告
学号: 3100100407_______课程名称:__电路原理实验______指导老师:__ 熊素铭______成绩:__________________实验名称:_一阶RC电路的暂态响应____实验类型:________________同组学生姓名:
__________
一、实验目的和要求(必填)二、实验内容和原理(必填
三、主要仪器设备(必填)四、操作方法和实验步骤
五、实验数据记录和处理六、实验结果与分析(必填)
七、讨论、心得
一、实验目的
1、熟悉一阶RC电路的零状态响应、零输入响应和全响应。
2、研究一阶电路在阶跃激励和方波激励情况下,响应的基本规律和特点。
3、掌握积分电路和微分电路的基本概念。
4、研究一阶动态电路阶跃响应和冲激响应的关系。
5、从响应曲线中求出RC电路时间常数τ。
二、实验原理
1.电路的过渡过程
2.一阶RC 电路的零输入响应: 激励(电源)为零,由初始储能引起的响应(放电过程)
1)求RC电路时间常数τ
3.一阶RC 电路的零状态响应: 储能元件初始能量为零,在激励(电源)作用下产生的
响应。
1)求RC电路时间常数τ
4.一阶RC 电路的全响应: 非零起始状态的电路受到外加激励所引起的响应。
5.
一阶RC 电路的方波响应: 从本质上看,方波是以相同的时间间隔,不停开关的电压(或者不断为高低值)。
6.微分电路和积分电路
1)微分电路:如图(1)RC电路,当输出电压取自电阻两端时,对于高频信号,可用作耦合
电路,而对于低频信号则可实现微分运算。
2)
积分电路
:如图(2)RC电路,当输出电压取自电容两端时,对于高频信号,可实现积分运算。
图(1)图(2)
7.冲激响应、阶跃响应及其关系:阶跃响应是阶跃函数激励下的零状态响应;冲激响应
是冲激函数激励下的零状态响应;冲激响应是阶跃响应的导数;
三、实验内容及数据记录分析
1.利用DG08动态电路板上的R、C元件组成RC充、放电电路,在示波器上观察零输
入响应、零状态响应和全响应曲线,测取电路时间常数τ (与理论值比较)。
1)观察的曲线图如下
零输入响应曲线零状态响应曲线全响应曲线
2)计算电路时间常数τ
2.选择合适的R、C值组成微分电路和积分电路,接入方波电压信号源,在示波器上观
察比较输入、
输出波形;比较改变时间常数后波形的变化情况。
信号源电压US = 3V , 频率 f= 1000Hz (保持不变)。
注:CH1为输出端;CH2为输入端;CH2-CH1为另外一个输出端
1)微分电路 T >> τ;R = 1 kΩ;C =0.1 μF
CH1
微分电路图
CH2 CH2-CH1
2)T = τ; R = 10 kΩ; C =0. 1 μF
CH1 CH2
CH2-CH1 积分电路图
3)积分电路 T << τ; R = 10 kΩ;C =1 μF
CH1 CH2 CH2-CH1 3)由以上三种情况的比较可知:
实验报告(仿真部分)
一、仿真内容:
1.记录一阶RC电路充放电时电容电压和电流的变化曲线,由曲线测得时间常数,并与理
论值比较。
2.记录积分电路和微分电路输入和输出波形;记录τ =0.1T、τ =T 和τ =10T、三种情况下
的波形。
二、仿真记录:
1.设计如下图的电路,进行仿真:
所得曲线图如下:
零输入响应零状态响应全响应
并用原理中的方法来计算,得到的时间常数τ=1.00,与理论值相符。
2.积分电路和微分电路输入和输出波形如下:
第一种情况:τ =0.1T;电路图如下:
相应输入输出图形如下:
Us U C U R 第二种情况:τ = T;电路图如下:
相应输入输出图形如下:
用心整理的精品word
文档,下载即可编辑!!
精心整理,用心做精品11
Us U R
U C
第三种情况:T = 10
τ;电路图如下:
相应输入输出图形如下:
Us U R U C。