下载文档原格式
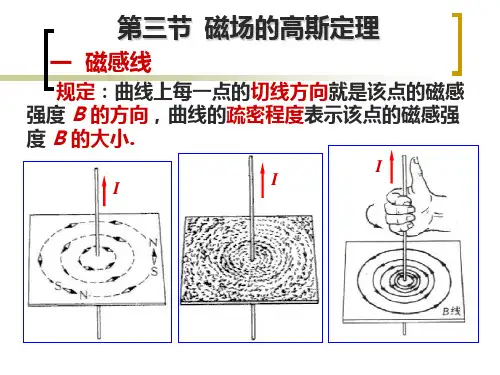
磁高斯定理
磁高斯定理（Maxwell's theorem）是磁力学的重要定理，由英国
物理学家乔治·马克斯韦（George Maxwell）于1865年提出。
它解释
了磁场的电流和旋转矢量之间的关系，是磁力学最根本的定律。
磁高斯定理可以用数学形式来表示：∇ × B = μ0J，其中B为
磁场，J为电流密度，μ0为真空磁导率（μ0=4π×10-7H/m），∇是
矢量求导运算符号。
这个定理描述了一个简单的物理现象：电流的旋
转产生了磁场，所以它是磁力学的基础。
磁高斯定理非常重要，可以解释各种电磁相关的现象。
它提供了
一种理解电磁学中电流向量、磁场强度和磁矢量之间关系的方法。
马
克斯韦在提出它的定理后，将电磁学理论推向了一个新的高度。
此外，磁高斯定理也可以用来解决电磁学中各种实际问题。
例如，它可以解释磁场强度的变化情况，从而帮助我们探索和分析电磁学现象。
总之，磁高斯定理是电磁学的基石，是磁力学的重要定理。
它不
仅能够精确地描述电磁学上的实际现象，而且可以结合其它电磁学定律，来求解一些复杂的实际问题。
磁场中的高斯定理公式
磁场中的高斯定理公式：∮EdS=(∑Q)/ε0，高斯定理也称为高斯通量理论，或称作散度定理、高斯散度定理、高斯－奥斯特罗格拉德斯基公式、奥氏定理或高－奥公式。
在静电学中，表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。
高斯定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定律在静电场情况下类比于应用在磁场学的安培定律，而二者都被集中在麦克斯韦方程组中。
因为数学上的相似性，高斯定律也可以应用于其它由平方反比律决定的物理量，例如引力或者辐照度。
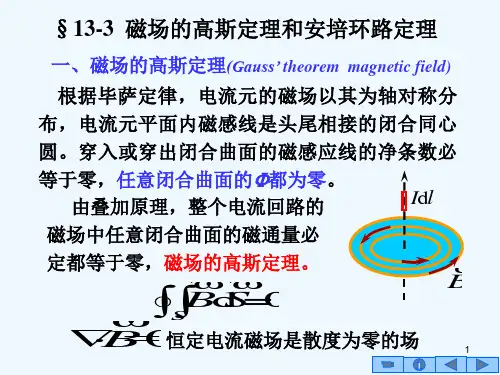
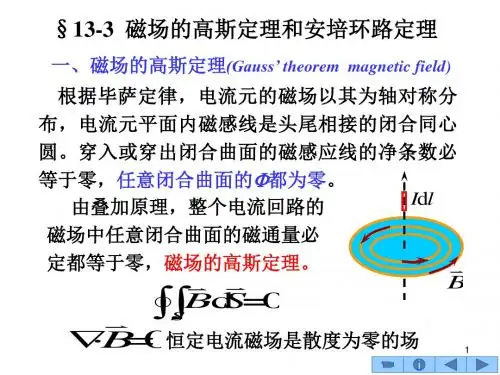
磁场高斯定理磁场的高斯定理：对于任意磁场B(r)B(r)和任意闭合曲面，曲面上的磁通量为零。
∮B(r)⋅ds=0(1)(1)∮B(r)⋅ds=0也就是说空间任意一点的磁场散度为零。
适用高斯定理可以写成微分形式：∇⋅B=0(2)(2)∇⋅B=0接下来我们试着验证一下这一结论是否和我们之前的理论是一致的，也就是说我们能否直接从比奥萨伐尔定律所给出的磁场B(r)B(r)推出，首先我们考虑静磁场下，电流是恒定的，因此电流密度j j不会在某一个点聚集或者散开，因此有：∇⋅j=0(3)(3)∇⋅j=0结合比奥萨伐尔：B(r)=μ04π∫j(r′)×(r−r′)|r−r′|3dV′(4)(4)B(r)=μ04π∫j(r′)×(r−r′)|r−r′|3dV′利用矢量乘法的规则可得：∇⋅(j×(r−r′)|r−r′|3)=(r−r′)|r−r′|3⋅(∇×j)−j⋅(∇×(r−r′)|r−r′|3)(5)(5)∇⋅(j×(r−r′)|r−r′|3)=(r−r′)|r−r′|3⋅(∇×j)−j⋅(∇×(r−r′)|r−r′|3)由于∇×(r−r′)|r−r′|3=0∇×(r−r′)|r−r′|3=0：∇⋅B=0(6)(6)∇⋅B=0注意磁场高斯定律适用于经典电动力学的任何情况，而后者只适用于静态的情况。
磁场的高斯定律实际上是电场的高斯定律在磁学中的对应，它反映了自然界没有孤立的磁单极（或者我们还没找到）。
形象地看，任意一条磁感线都不会起始或终止于空间中的某一点，它要么是闭合的回路，要么从无穷远来延伸到无穷远去。
正因为磁场的这条性质，我们可以将磁感应强度B B写成某个矢量场A A的旋度，其中A A称为矢量势（矢势）。
